Robust Transiting Exoplanet Radii in the Presence of Starspots from Ingress and Egress Durations

Precise and accurate radii of exoplanets are critical to understanding their habitability. Radii are often used as a proxy for bulk composition when masses are not available, informed by population studies which suggest that planets smaller than R ≲ 1.5 R_⊕ are more likely rocky than gaseous (Weiss & Marcy 2014; Rogers 2015; Fulton et al. 2017). Since bulk densities are sensitive to the radius to the third power, accurate radii are required in order to infer accurate bulk densities.

The radii of transiting exoplanets are typically constrained by the transit depth, which is interpreted as the ratio of the cross-sectional areas of the planet and star ${\rm{\Delta }}{ \mathcal F }/{ \mathcal F }={({R}_{p}/{R}_{\star })}^{2}$ (ignoring limb-darkening). The transit depth accuracy as a measure of the planet’s radius, however, is sensitive to stellar surface inhomogeneities. When planets pass over dark starspots, for example, the transit light curve is biased toward shallower transit depths during the transit (see, e.g., Csizmadia et al. 2013; Oshagh et al. 2013). As we discover more planetary systems of late-type stars like TRAPPIST-1 (Gillon et al. 2016, 2017; Luger et al. 2017), the time- and wavelength-dependent variability of these active stars and non-uniformity is likely to limit the accuracy and precision of our measurements of the planet radii, especially as a function of wavelength (Roettenbacher & Kane 2017; Morris et al. 2018a; Rackham et al. 2018; Zhang et al. 2018).

Particularly insidious are nearly axisymmetric stellar inhomogeneities and/or inhomogeneities comprised of odd harmonics. These do not lead to variability in the total flux of the star, and do not necessarily cause spot-crossing features in the transit light curve; yet they will still affect the depth of transit, and hence the inferred planet–star radius ratio and transmission spectrum. Consequently, even without indications of starspot activity in the light curve of a star, spots (or other inhomogeneities) can still affect the depths of transits; this phenomenon is referred to as the “transit light source effect” in the recent work by Rackham et al. (2018). These forms of time-steady “activity” might be due to a multitude of starspots (such as along a particularly active latitude), due to gravity darkening, or due to a strong global magnetic field. The message of this paper is that if one measures the duration of ingress as compared to the total transit duration, this time-dependent quantity will be less affected by the presence of spots on the rest of the photosphere, and thus may give a more precise, albeit less accurate, measurement of the planet–star radius ratio compared with measuring the radius ratio from the depth of transit. However, in most cases it does require an independent constraint upon the impact parameter of the transit, as well as a careful handling of limb-darkening.

In Section 2 we reparameterize the transit light curve formalism of Mandel & Agol (2002) for more robust planet radii in the presence of significant starspot coverage, and elaborate on the degeneracies in the model in Section 3. In Section 4, we validate the new transit model with fits to synthetic light curves of simulated spotted stars. We fit real transit light curves of a variety of planets including TRAPPIST-1 and GJ 1214 in Section 5, and discuss the results and conclusions in Sections 6 and 7.

Following Mandel & Agol (2002), the ratio of unocculted flux to occulted flux F is given by

$$\begin{eqnarray}&&{F}^{e}({p}_{0},z,{u}_{1},{u}_{2})=1-{\lambda }^{e}({p}_{0},z,{u}_{1},{u}_{2}),\end{eqnarray} \tag{ 1 }$$

where p₀ = R_p/R_⋆, z is the projected sky separation between the centers of the star and planet (in units of the stellar radius), and u₁ and u₂ are the quadratic limb-darkening parameters. One way to interpret the transit light curve—for a star known to have little contamination from other nearby stars—is to create a flux contamination term which will account for bright or dark regions of the surface of the star known to be transited. We introduce the new parameter p₁ and renormalize the λ term as:

$$\begin{eqnarray}&&{F}^{e}({p}_{1},{p}_{0},z,{u}_{1},{u}_{2})=1-{\left(\displaystyle \frac{{p}_{1}}{{p}_{0}}\right)}^{2}{\lambda }^{e}({p}_{0},z,{u}_{1},{u}_{2}).\end{eqnarray} \tag{ 2 }$$

It follows that ${p}_{1}\approx \sqrt{\delta }$ where δ is the transit depth (the approximation becomes an equivalence for the uniform case where u₁ = u₂ = 0). We emphasize here that p₁ is not a radius ratio parameter like p₀; ${p}_{1}^{2}$ is related to the observed transit depth in the presence of bright or dark spot contamination. A measured difference between p₀ and p₁ is in principle sensitive to starspots, even with an axisymmetric distribution, unlike rotational modulation.

This renormalization is equivalent to the analysis often performed on Kepler planet candidate host stars in order to search for contaminating light from a second, unresolved star (Torres et al. 2011; Morton 2012; Teske et al. 2018). Typically in the external contamination case, the light from the background star dilutes the flux of the exoplanet host star, decreasing the transit depth, modifying the inferred impact parameter, and leading to underestimating the planet radii, if the contamination is unaccounted for.

In Equation (2), we are essentially allowing for a contaminating light source on the host star itself, which can be positive or negative due to bright or dark regions on the stellar surface, thus increasing or decreasing the transit depth ${p}_{1}^{2}$ with respect to the expectation given the planet’s radius p₀. Typically for contaminating nearby sources, the ratio of the unocculted flux to occulted flux is given by

$$\begin{eqnarray}&&{F}^{e}=(1-{\lambda }^{e})(1-\epsilon )+\epsilon ,\end{eqnarray} \tag{ 3 }$$

where is the flux of the contaminating source. In this parameterization,

$$\begin{eqnarray}&&{\left(\displaystyle \frac{{p}_{1}}{{p}_{0}}\right)}^{2}=1-\epsilon .\end{eqnarray} \tag{ 4 }$$

We focus our attention in this work on the “self-contamination” effect of bright or dark regions on the host star itself.

We have implemented the algorithm in CPython called robin, based on a fork of the batman code by Kreidberg (2015), which is publicly available.⁴

Given the untoward effect of contamination on measurement of the planet–star radius ratio, we require some additional constraint to derive this ratio in the presence of a heterogenous stellar photosphere or blending with other sources of light. This can be provided by a purely geometrical constraint: the ratio of ingress duration to transit duration. However, to implement this requires a knowledge of (or constraint upon) the impact parameter of the transit, b, which we describe in this section.

The duration of ingress for an eccentric orbit is given approximately by:

$$\begin{eqnarray}&&\tau =\displaystyle \frac{2{R}_{p}}{v\sin \theta },\end{eqnarray} \tag{ 5 }$$

where θ is the angle between the tangent of the limb of the star and the path of the planet (projected onto the sky plane) and v is the sky velocity of the planet relative to the star during transit, which we take to be constant in this section. The duration of the transit, T, from mid-ingress to mid-egress is given by

$$\begin{eqnarray}&&T=\displaystyle \frac{2{R}_{* }\,\sin \theta }{v}.\end{eqnarray} \tag{ 6 }$$

Now $\sin \theta =\sqrt{1-{b}^{2}}$, so

$$\begin{eqnarray}&&\tau =2{(1-{b}^{2})}^{-1/2}\displaystyle \frac{{R}_{p}}{{R}_{* }}\displaystyle \frac{{R}_{* }}{v},\end{eqnarray} \tag{ 7 }$$

$$\begin{eqnarray}&&T=2{(1-{b}^{2})}^{1/2}\displaystyle \frac{{R}_{* }}{v}.\end{eqnarray} \tag{ 8 }$$

These formulae assume that $a\gg {R}_{* }$ and ${R}_{p}\ll {R}_{* }$, neglecting the curvature of the orbit and the stellar limb (see Winn et al. 2010 or Appendix A for more complete relations).

The transit and ingress/egress durations are simply a function of time, and do not depend upon the transit depth, and hence will not be affected by dilution by starspots or flux from a blend, such as a companion star. Thus, a precise measurement of τ and T can in principle give another means of constraining the radius ratio of the planet to the star which will be less affected by blending or a heterogeneous stellar photosphere.

There are two ways to solve for this radius ratio, the first of which is derived from the ratio of ingress to duration of transit,

$$\begin{eqnarray}&&\displaystyle \frac{{R}_{p}}{{R}_{* }}=\displaystyle \frac{\tau }{T}(1-{b}^{2}).\end{eqnarray} \tag{ 9 }$$

This requires a constraint upon the impact parameter, b. The shape of ingress and egress depends weakly on the impact parameter; however, this is generally too subtle to measure, even with the highest signal-to-noise ratio (S/N) transits. Note that given measured values of τ and T imply a maximum value of R_p/R_*, which is the value this ratio would have if b = 0. This could be useful for placing upper limits on the radii of planets given measured properties of the transit; this constraint is independent of the eccentricity and period of an orbit, and of the density of the star. If the depth of transit (as parameterized by ${p}_{1}^{2}$) implies a radius ratio that is greater than this maximum value, then this likely implies that both a small impact parameter and that non-transited starspots must be present (or that the planet transits a bright chord) to cause a larger transit depth, or that the planet is significantly oblate (see the next section).

The second means of solving for the radius ratio from time-dependent quantities is given by

$$\begin{eqnarray}&&\displaystyle \frac{{R}_{p}}{{R}_{* }}=\displaystyle \frac{\tau T}{4}{\left(\displaystyle \frac{v}{{R}_{* }}\right)}^{2},\end{eqnarray} \tag{ 10 }$$

which requires a measurement of the normalized sky velocity, given by

$$\begin{eqnarray}&&\displaystyle \frac{v}{{R}_{* }}=\displaystyle \frac{2\pi }{P}\displaystyle \frac{a}{{R}_{* }}\displaystyle \frac{1+e\sin \omega }{\sqrt{1-{e}^{2}}},\end{eqnarray} \tag{ 11 }$$

$$\begin{eqnarray}&&\displaystyle \frac{a}{{R}_{* }}={\left[\displaystyle \frac{G{\rho }_{* }{P}^{2}}{3\pi }\right]}^{1/3},\end{eqnarray} \tag{ 12 }$$

where ρ_* is the stellar density, e is the orbital eccentricity, and ω is the longitude of periastron of the star measured along the orbital path from when the star crosses the sky plane away from the observer.⁵ Thus, if a/R_* is constrained, for example, from asteroseismology or asterodensity profiling (which requires additional transiting planets), and if the eccentricity vector, $\overrightarrow{e}=\{e\cos \omega ,e\sin \omega \}$ is constrained, for example, from radial velocity measurements or transit-timing variations, then the transit chord, $d/{R}_{* }=2\sqrt{1-{b}^{2}}$ (in units of R_*), and hence the impact parameter, can be constrained from the transit duration.

In practice, then, the radius ratio may only be determined in cases for which there is a prior on the impact parameter, and generally this is derived from the dependence of the transit duration upon the stellar density and the eccentricity of the planet’s orbit, as well as other well-measured quantities such as the planet’s orbital period. The formulae above are only approximate as they neglect the curvature of the orbit and the curvature of the limb of the star (see Appendix A for more general expressions), but these relations are generally good approximations, while the full relation can be accounted for with a full orbital transit model.

3.1. Planetary Oblateness

The preceding analysis assumes that a planet is spherical. However, the transit depth and the duration of ingress and egress are also affected by its shape. If a planet is distorted, for example, due to oblateness, then its area and the distance it moves during ingress and egress are not simply related to its mean radius. Oblateness can be induced by rotation of a planet, causing a bulging of the equator due to centripetal acceleration (Barnes & Fortney 2003), or by its thermal structure, causing a larger scale height at the hotter equator relative to the poles (Dobbs-Dixon et al. 2012). There are several references in the literature which fully consider the transits of oblate planets, and we refer the interested reader to Hui & Seager (2002), Barnes & Fortney (2003), Carter & Winn (2010), Zhu et al. (2014), and Biersteker & Schlichting (2017).

In addition to bright or dark active regions and contaminating light sources, planetary oblateness can cause a mismatch between the observed values of p₀ and p₁. Here we derive a relationship between p₀, p₁, and the oblateness of the planet,

$$\begin{eqnarray}&&f=\displaystyle \frac{{R}_{\mathrm{eq}}-{R}_{\mathrm{pole}}}{{R}_{\mathrm{eq}}}.\end{eqnarray} \tag{ 13 }$$

The projected ellipsoid of an oblate planet with semimajor axis α (in units of R_⋆) and semiminor axis β makes first contact with the star at point P, see Figure 1, which is an angle θ from the semimajor axis of the planet (or the $+\hat{X}$ axis in the planet-centered coordinate system). The angle from the $+\hat{X}$-axis to the normal of the tangent of the ellipse is ψ  = sin⁻¹(b), where b is the impact parameter.

Zoom In Zoom Out Reset image size

The definition of the elliptical outline of the planet r is

$$\begin{eqnarray}&&{r}^{2}={\alpha }^{2}{\cos }^{2}\theta +{\beta }^{2}{\sin }^{2}\theta ,\end{eqnarray} \tag{ 14 }$$

and the slope of a tangent line which meets the ellipse at point P is

$$\begin{eqnarray}&&m=-\displaystyle \frac{\beta }{\alpha }\cot \theta =-\cot \psi .\end{eqnarray} \tag{ 15 }$$

We assume for simplicity that the major axis of the oblate planet is aligned along its direction of motion relative to the star, so α = R_eq/R_* and $\beta ={R}_{\mathrm{pole}}/{R}_{* }$. Now we can solve for p₀ given

$$\begin{eqnarray}&&{p}_{0}=r\cos (\psi -\theta )\end{eqnarray} \tag{ 16 }$$

where ψ is the angle measured up from the $+\hat{X}$ axis to p₀. Solving for p₀ in terms of α, β,

$$\begin{eqnarray}&&{p}_{0}=\alpha \displaystyle \frac{\sqrt{1-{b}^{2}+{b}^{2}{(1-f)}^{4}}}{1-{b}^{2}+{b}^{2}{(1-f)}^{2}}(1-{b}^{2}f).\end{eqnarray} \tag{ 17 }$$

Note that in the oblate planet case f > 0, ${p}_{0}\ne \alpha$ for non-zero b. The depth of the transit will be the ratio of the cross-sectional area of the planet to the star,

$$\begin{eqnarray}&&{p}_{1}^{2}=\alpha \beta ,\end{eqnarray} \tag{ 18 }$$

so the general form of the relation between p₀, p₁, b and f is

$$\begin{eqnarray}&&{\left(\displaystyle \frac{{p}_{1}}{{p}_{0}}\right)}^{2}=\displaystyle \frac{(1-f){(1-{b}^{2}+{b}^{2}{(1-f)}^{2})}^{2}}{{(1-{b}^{2}f)}^{2}(1-{b}^{2}+{b}^{2}{(1-f)}^{4})}\end{eqnarray} \tag{ 19 }$$

$$\begin{eqnarray}&&\approx \,1-f(1-2{b}^{2}),\end{eqnarray} \tag{ 20 }$$

where the last expression is valid for $f\ll 1$. In the special case where b = 0, this simplifies to

$$\begin{eqnarray}&&{\left(\displaystyle \frac{{p}_{1}}{{p}_{0}}\right)}^{2}=1-f,\end{eqnarray} \tag{ 21 }$$

implying that ${p}_{0}^{2}={\alpha }^{2}\,$=$\,{R}_{\mathrm{eq}}^{2}/{R}_{* }^{2}$ and ${p}_{1}^{2}=\alpha \beta ={R}_{\mathrm{pole}}{R}_{\mathrm{eq}}/{R}_{* }^{2}$.

To estimate the ability to measure the planet–star radius ratio in the presence of a heterogeneous stellar photosphere, we used the reparameterized transit light curve to fit simulated light curves generated with STSP⁶ . STSP synthesizes transit light curves of spotted stars by analytically computing the overlap between the planet, starspots, and the star, with limb darkening approximated by concentric circles of constant surface brightness.

We consider two axisymmetric starspot distributions: the first in which the planet’s orbital angular momentum is aligned with that of the star in the sky plane, and the planet crosses an active latitude with dark spots, and the second in which active latitudes are present with dark spots, but not transited by the planet. This first case causes shallower transits relative to a uniform star, which is equivalent to contamination by an additional source with  > 0, while the second case causes deeper transits, and is equivalent to dilution by a source with negative flux,  < 0, which is the deficit of stellar flux caused by the darker spots.

4.1. Occultation of an Active Latitude

We synthesize a transit light curve of a star with a dense band of spots that blankets the stellar equator using STSP with c = 0.7; see Figure 2. We observe the transit at one second cadence with uncertainties of 48 ppm for each flux measurement, which is similar in scale to the oscillations in flux at the “bottom” of the transit light curve, such that fits to the transit light curve with the standard (Mandel & Agol 2002) model yield a reduced-χ² = 0.95. This is a very high-S/N example, even exceeding reasonable S/N estimates for bright targets observed with the James Webb Space Telescope (JWST). The corresponding transit light curve for a planet with impact parameter b = 0 and projected spin–orbit alignment λ = 0° (i.e. the planet transits the stellar equator) is shallower than the transit of the same system without starspots. The duration of ingress and egress independently encode the radius of the planet.

Zoom In Zoom Out Reset image size

Figure 3 shows the posterior distributions of fits for the parameters p₀, p₁ for the spotless (left) and spotted (right) light curves, allowing the impact parameter and transit duration T₁₄ to vary, and holding the limb-darkening parameters fixed at their true values. In the spotless light curve case, as expected, we find that p₀ = p₁. In the case of transiting an active latitude of dark spots, p₀ > p₁, indicating that the transit depth is being decreased by occultations of dark starspots. The solution for p₀ is consistent with the injected transit radius p₀ = R_p/R_⋆ = 0.05971.

Zoom In Zoom Out Reset image size

The degeneracy between p₀, the limb-darkening parameters, and the impact parameter becomes increasingly important as one decreases the S/N of the observations. For example, we inflated the uncertainties on each observation by a factor of three, and found that the uncertainties on p₀, impact parameter, and limb-darkening parameters increased by factors of 5, 2, and 2, respectively. This exercise demonstrates the importance of having independent measurements of the impact parameter or a/R_⋆, as discussed in Section 3.

4.2. Occultation of a Bright Latitude

We approximate a bright latitude centered on the stellar equator with STSP by creating active latitudes of spots centered on ±30° latitude, see Figure 4, while keeping the same planet properties and uncertainties as in Section 4.1. The planet transits a relatively bright region of the stellar surface, so in this example the transit light curve for the spotted star is deeper than expected for the spotless case.

Zoom In Zoom Out Reset image size

Figure 5 shows the posterior distribution of fits for the parameters p₀, p₁ for the spotless (left) and spotted (right) light curves, allowing the impact parameter and transit duration T₁₄ to vary, and holding the limb-darkening parameters fixed at their true values, as in Section 4.1. In the spotless light curve case, we again find that p₀ = p₁. In the case of transiting a bright latitude, p₀ < p₁, indicating that the transit depth is being increased by the spot distribution. The solution for p₀ is again consistent with the injected transit radius p₀ = R_p/R_⋆ = 0.05971.

Zoom In Zoom Out Reset image size

We consider further limiting cases with extreme spot distributions in Appendix B, which suggests that plausible limits for self-contamination are $-0.5\lesssim \epsilon \equiv$ $\,1-{({p}_{1}/{p}_{0})}^{2}\lesssim 0.5$.

4.3. Required Precision

It is important to note that extremely high S/N light curves are required to produce meaningful constraints on the difference between p₀ and p₁, similar to the S/N assumed in the previous two subsections. Descriptions of the uncertainties on p₀ and p₁ in terms of planetary system and observing parameters are detailed in Appendix C. Here we will take the examples of the previous two subsections and ask what photometric precision is necessary to measure significant deviations between p₀ and p₁.

Figure 6 shows the confidence interval for detecting p₀ < p₁ when crossing a dark latitude with the spot map from Section 4.1, as a function of photometric precision on one-second cadence observations of TRAPPIST-1 g (left); and the confidence interval for detecting p₀ > p₁ when crossing a bright latitude with the spot map from Section 4.2 (right). For the TRAPPIST-1 g system in particular, extremely high S/N precision—tens of ppm uncertainty per flux measurement—would be required to significantly detect the occultation of a dark latitude. The situation is a little less severe for the occultation of a bright latitude: hundreds of ppm uncertainty per flux measurement are sufficient to significantly detect p₀ < p₁ in this case. In each case, we note that the required precision is similar to or better than the precision achievable with phase-folded Kepler observations, so we anticipate that any detections of spot distributions with the self-contamination technique from Kepler observations (Section 5.1) will yield only marginal significance, and higher S/N observations, like those of the JWST, may be able to achieve the precision necessary to unambiguously separate the posterior distributions of p₀ and p₁.

Zoom In Zoom Out Reset image size

5.1. Kepler Light Curves

We apply the new parameterization to the highest S/N transit light curves available—those of the transiting planets Kepler-1, Kepler-2 and Kepler-3 (a.k.a. TrES-2, HAT-P-7, and HAT-P-11). Each of these light curves has short cadence observations throughout the Kepler mission, short-period planets, and very bright host stars (K_p = 9.84, 9.33, 7.00, respectively). As a result, these light curves should yield some of the best constraints on ingress and egress durations available. We also explore some exceptional cases: the highly spotted star Kepler-17, the potentially oblate planet Kepler-39 b, and a planet with a vary high impact parameter, and thus long ingress/egress durations, Kepler-412.

For Kepler-1 through -3, the Kepler Input Catalog estimated contamination in the Kepler aperture is ≲1%, so a third light source can likely be ruled out as the cause for discrepancies between p₀ and p₁ for these targets (Brown et al. 2011). For Kepler-17, -39 and -412, the contamination is ≲6%, so discrepancies larger than 6% are required to invoke stellar activity as the culprit for disagreement between p₀ and p₁.

For each Kepler transit light curve, we normalize the simple aperture photometry (SAP) flux by a quadratic fit to the out-of-transit flux. We assume the periods, midtransit epochs, eccentricities, and arguments of periastron for each target listed in the NASA Exoplanet Archive.

5.1.1. TrES-2 (Kepler-1)

TrES-2 is a G0V star with T_eff = 5960 ± 100 K and $\mathrm{log}g=4.4\pm 0.2$ (O’Donovan et al. 2006; Sozzetti et al. 2007). Asteroseismology indicates M = 0.94 ± 0.05 M_⊙ and R = 0.95 ± 0.02 R_⊙, and the stellar age is 5.8 ± 2.2 Gyr (Barclay et al. 2012). The Rossiter–McLaughlin effect shows the orbit of its hot-Jupiter is prograde (Winn et al. 2008). TrES-2 is an especially enticing target because its high impact parameter, b = 0.84, provides us with long ingress and egress durations and therefore tighter constraints on p₀.

We fit the transit light curve in Figure 7 for p₀, p₁, i_o, a/R_⋆, holding the quadratic limb-darkening parameters fixed at u₁, u₂ = 0.39256, 0.29064 (Magic et al. 2015). The posterior distributions of p₀ and p₁ are overlapping, indicating that the planet radius inferred from the transit depth is consistent with that inferred from the ingress and egress durations (see Figure 7). This measurement aligns with our expectation for a middle-aged, solar-like star such as TrES-2, since sunspots typically cover ∼0.03% of the solar surface (Howard et al. 1984). We note that the quadratic limb-darkening parameters of Magic et al. (2015) appear to be sufficient for describing the transit of this G0 star even at extremely high S/N. Table 1 reports the results from this analysis.

Zoom In Zoom Out Reset image size

Table 1.  Maximum-likelihood Parameters for p₀, p₁, the Self-contamination Parameter $\epsilon =1-{({p}_{1}/{p}_{0})}^{2}$, and the Confidence Interval (CI) for Each Detection of p₀ Relative to p₁

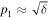
Target	p0 = Rp/R⋆	${p}_{1}\approx \sqrt{\delta }$		Condition	CI
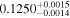
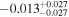
TrES-2	${0.1250}_{-0.0014}^{+0.0015}$	${0.12590}_{-0.00017}^{+0.000168}$	$-{0.013}_{-0.027}^{+0.027}$	p0 < p1	71%
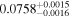
HAT-P-7	${0.0758}_{-0.0016}^{+0.0015}$	${0.07744}_{-0.00013}^{+0.00015}$	$-{0.042}_{-0.050}^{+0.044}$	p0 < p1	85%
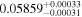
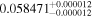
HAT-P-11	${0.05859}_{-0.00031}^{+0.00033}$	${0.058471}_{-0.000012}^{+0.000012}$	${0.004}_{-0.010}^{+0.011}$	p0 > p1	66%
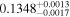
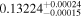
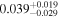
Kepler-17	${0.1348}_{-0.0017}^{+0.0013}$	${0.13224}_{-0.00015}^{+0.00024}$	${0.039}_{-0.029}^{+0.019}$	p0 > p1	93%
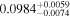
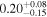
Kepler-39	${0.0984}_{-0.0074}^{+0.0059}$	${0.08813}_{-0.00041}^{+0.00062}$	${0.20}_{-0.15}^{+0.08}$	p0 > p1	90%
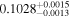
Kepler-412	${0.0909}_{-0.0065}^{+0.0083}$	${0.1028}_{-0.0013}^{+0.0015}$	$-{0.28}_{-0.22}^{+0.22}$	p0 < p1	90%
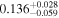
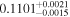
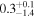
GJ 1214	${0.136}_{-0.059}^{+0.028}$	${0.1101}_{-0.0015}^{+0.0021}$	${0.3}_{-1.4}^{+0.1}$	p0 > p1	71%
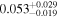
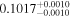
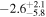
HD 80606	${0.053}_{-0.019}^{+0.029}$	${0.1017}_{-0.0010}^{+0.0010}$	$-{2.6}_{-5.8}^{+2.1}$	p0 < p1	96%
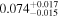
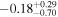
TRAPPIST-1 b	${0.074}_{-0.015}^{+0.017}$	${0.0859}_{-0.0007}^{+0.0006}$	$-{0.18}_{-0.70}^{+0.29}$	p0 < p1	74%
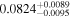
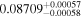
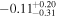
TRAPPIST-1 c	${0.0824}_{-0.0095}^{+0.0089}$	${0.08709}_{-0.00058}^{+0.00057}$	$-{0.11}_{-0.31}^{+0.20}$	p0 < p1	70%

Download table as:  ASCIITypeset image

5.1.2. HAT-P-7 (Kepler-2)

HAT-P-7 is a slightly evolved F6 star, orbited by a highly misaligned hot-Jupiter (Pál et al. 2008; Winn et al. 2009b). Asteroseismology indicates that the star is likely in a pole-on configuration (Benomar et al. 2014; Lund et al. 2014). Several authors have noted that there is a ∼20 ppm positive residual bump in the transit light curve between ingress and mid-transit, which may be attributed to stellar gravity darkening (van Eylen et al. 2012; Morris et al. 2013; Masuda 2015).

We fit the phase-folded Kepler light curve of HAT-P-7 for p₀, p₁, a/R_⋆, i_o, t₀ and the four nonlinear limb-darkening parameters. We put a Gaussian prior on a/R_⋆ with the value inferred from asteroseismology by Lund et al. (2014), $\langle {\rho }_{\star }\rangle \,$=$\,0.266\,\pm 0.008\,$ g cm⁻³ or a/R_⋆ = 4.090 ± 0.044. The results are shown in Figure 8. We find that p₀ ≈ p₁, indicating that the transit chord of the planet is representative of the typical intensity of the star, despite the gravity-darkening signal evident in the transit residuals. This would appear to be a result of the stellar orientation, with its bright pole being occulted between mid-transit and egress, and its dimmer low latitudes being occulted between ingress and mid-transit. The net effect of the gravity darkening on the light curve residuals appears to cancel out since p₀ is consistent with p₁

Zoom In Zoom Out Reset image size

5.1.3. HAT-P-11 (Kepler-3)

HAT-P-11 is a benchmark system for studying stellar activity with planetary transits. It is a 0.8M_⊙ star with a rotation period similar to the Sun (P_rot = 29 day) (Bakos et al. 2010; Sanchis-Ojeda & Winn 2011; Southworth 2011; Deming et al. 2011). In Morris et al. (2017a, 2017b, 2018b) we establish qualitative similarities between the Sun and HAT-P-11's starspot distributions and activity cycles.

We fit the phase-folded Kepler light curve of HAT-P-11 for p₀, p₁, a/R_⋆, i_o, t₀ and quadratic limb-darkening parameters. We place a Gaussian prior on a/R_⋆ with the value inferred from asteroseismology by Christensen-Dalsgaard et al. (2010), $\langle {\rho }_{\star }\rangle =2.5127\pm 0.0009$ g cm${}^{-3}\,\Rightarrow a/{R}_{\star }=14.6950\pm 0.0017$, and fix the eccentricity and argument of periastron to the measurements of Winn et al. (2010). The results are shown in Figure 9. We find p₀ ≈ p₁, indicating that the spot-covering fraction is relatively small.

Zoom In Zoom Out Reset image size

It is interesting to compare the spot-covering fractions measured in- and out-of-transit for HAT-P-11 from Morris et al. (2017b). The Kepler light curve shows ∼3% rotational modulation each quarter. If we assume the starspots have contrast similar to sunspots, we can use Equations (9)–(14) of Morris et al. (2017b) to estimate the spot-covering fraction within the transit chord from p₀ and p₁ by noticing that the depth of transit will be diluted by starspots with contrast c (where c = 1 means spots with the same intensity as the photosphere and c = 0 means spots that are perfectly dark), and covering fraction f_S,

$$\begin{eqnarray}&&{p}_{1}^{2}\approx {p}_{0}^{2}(1-{f}_{S,\mathrm{transit}}(1-c)).\end{eqnarray} \tag{ 22 }$$

For example, if the transit chord is completely covered (f_S = 1) by perfectly dark spots (c = 0), then the transit depth goes to zero. If the transit chord has Sun-like spots with c = 0.7, then we can solve for the spot-covering fraction given p₀ and p₁,

$$\begin{eqnarray}&&{f}_{S,\mathrm{transit}}\approx \displaystyle \frac{1}{1-c}\left(1-{\left(\displaystyle \frac{{p}_{1}}{{p}_{0}}\right)}^{2}\right).\end{eqnarray} \tag{ 23 }$$

For HAT-P-11, this yields the spot-covering fraction in the transit chord f_S,transit ≈ 0.01 ± 0.03. We can compare the in-transit spot coverage to the spot-covering fraction that one would estimate from the flux deficit method (Morris et al. 2017b), which estimates the asymmetric component of the spot-covering fraction on the whole star via

$$\begin{eqnarray}&&{f}_{S,\mathrm{asym}}\gtrsim (1-\min (f))/(1-c),\end{eqnarray} \tag{ 24 }$$

or ${f}_{S,\mathrm{asym}}\gtrsim {0.03}_{-0.01}^{+0.06}$ for HAT-P-11. Detailed spot occultation modeling from Morris et al. (2017b) yields spot-covering fractions of 0%–10% within the chord of any given transit, broadly consistent with the small covering fraction measured with the self-contamination technique.

We note that, due to the significant obliquity of the orbit of the planet relative to the spin of the star, the time-averaged surface brightness contrast of the transit chord may match the stellar disk as the spots traverse about the same fraction of the stellar disk as they do of the transit chord. Consequently, the lack of detection in this case may be hampered by this geometry.

5.1.4. Estimating Stellar Densities in the Absence of Asteroseismology

When a star lacks an asteroseismic density measurement, the three-way degeneracy between p₀, the limb-darkening parameters, and the impact parameter (or equivalently a/R_⋆ or ρ_⋆) must be broken in order to produce meaningful constraints on p₀. For the following three planetary systems, Kepler-17, -39 and -412, no asteroseismic density is available in the literature.

We can estimate the stellar densities for stars without asteroseismic measurements by noting the tight correlation between stellar radius and density found in the asteroseismic sample of Huber et al. (2013); see Figure 10. For bright Kepler targets, Huber et al. (2013) used asteroseismology to calculate stellar densities, and isochrone models to predict stellar radii and masses. We fit a power law to the measured stellar densities as a function of radius, and find

$$\begin{eqnarray}&&{\mathrm{log}}_{10}({\rho }_{\star }[{\rm{g}}\ \,\ {\mathrm{cm}}^{-3}])\\ &&=\,(-2.540\pm 0.087){\mathrm{log}}_{10}({R}_{\star }/{R}_{\odot })+(0.12\pm 0.001),\end{eqnarray} \tag{ 25 }$$

with fractional scatter in ρ_⋆ of 0.083. Then for each star, we use the Gaia DR2 (Gaia Collaboration et al. 2018) stellar radius measurements from Berger et al. (2018) in combination with Equation (25) to predict the stellar density.

Zoom In Zoom Out Reset image size

At each step in our Markov chains for Kepler-17, -39 and -412, we sample for the parameters M_⋆ and R_⋆, placing a Gaussian prior on R_⋆ with the value and uncertainty from Gaia (Berger et al. 2018) (R_⋆ = 1.01 R_⊙, 1.23 R_⊙, and 1.35 R_⊙ for Kepler-17, -36, and -412, respectively), and placing a Gaussian prior on the stellar density following Equation (25) with fractional uncertainty 0.083 g cm⁻³.

5.1.5. Kepler-17

Kepler-17 is an active G2V star with T_eff = 5630 ± 100 K and age 3 ± 1.6 Gyr, with a hot Jupiter companion that produces starspot occultations in nearly every transit studied by Désert et al. (2011) and Davenport (2015). Thus Kepler-17's geometry is similar to the toy model in Section 4.1, where a planet occults an active latitude with many starspots, diluting the transit depth, and in which the stellar spin axis is aligned (in this case, to within 15°).

We fit the phase-folded Kepler light curve of Kepler-17 for p₀, p₁, b, t₀, T₁₄, M_⋆, R_⋆, and quadratic limb-darkening parameters. We place priors on M_⋆ and R_⋆ as described in Section 5.1.4. The results shown in Figure 11 indicate p₀ > p₁ at 93% confidence (∼2σ), in agreement with our expectation that starspot occultations dilute the apparent transit depth. We measure ${p}_{0}={R}_{p}/{R}_{\star }={0.1354}_{-0.0014}^{+0.0010}$, which is significantly larger than the Désert et al. (2011) estimate (${R}_{p}/{R}_{\star }={0.13031}_{-0.00018}^{+0.00022}$).

Zoom In Zoom Out Reset image size

As we did for HAT-P-11 in Section 5.1.3, we can compare the spot-covering fractions measured in- and out-of-transit for Kepler-17. The Kepler light curve shows ∼4% rotational modulation each quarter. If we assume the starspots have contrast similar to sunspots, as in Davenport (2015), we can use Equation (23) to estimate the spot-covering fraction within the transit chord and find ${f}_{S,\mathrm{transit}}\approx {0.27}_{-0.18}^{+0.12}$. We can compare the in-transit spot coverage to the spot-covering fraction that one would estimate from the flux deficit method, f_S,asym ≳ 0.13. These two measurements are consistent, and perhaps suggest that the transit chord may be more spotted than the mean photosphere, consistent with the apparent equatorial active latitude deduced from detailed spot modeling by Davenport (2015).

5.1.6. Kepler-39

Kepler-39 is a young F7V host star with T_eff = 6350 ± 100 K, and age ${0.7}_{-0.3}^{+0.9}$ Gyr (Mamajek & Hillenbrand 2008; Bonomo et al. 2015). Zhu et al. (2014) claim its 20 M_J companion has nonzero oblateness $f={0.22}_{-0.11}^{+0.11}$.

We fit the phase-folded Kepler light curve of Kepler-39 for p₀, p₁, b, t₀, T₁₄, M_⋆, R_⋆, and quadratic limb-darkening parameters. We place priors on M_⋆ and R_⋆ as described in Section 5.1.4. The results are shown in Figure 12. Zhu et al. (2014) measure R_p/R_⋆ = 0.0889 ± 0.0006 with their oblate planet model, consistent with our maximum likelihood p₀ = R_p/R_⋆ = 0.090 ± 0.010. We find that p₀ > p₁ with 90% confidence, suggesting weak evidence for either starspot occultations in the transit light curve, or the degenerate signal of planetary oblateness. We find $f={0.25}_{-0.06}^{+0.13}$, consistent with the oblateness reported by Zhu et al. (2014).

Zoom In Zoom Out Reset image size

However, we caution that the Kepler light curve shows rotational modulation of the star consistent with starspot coverage (see Figure 13), albeit several times smaller than for Kepler-17. We can estimate the minimum spot-covering fraction from the amplitude of the rotational modulation, which gives us a constraint on the asymmetry of the spot distribution as the star rotates, ${f}_{S,\min }\,\geqslant \,(1-\min {\rm{flux}})/(1-c)$ where c = 0.7 is the spot contrast for sunspots (Solanki 2003). Thus assuming spots with the contrast of sunspots, f_S,min ≥ 2%: a factor of ≳100 greater than the typical sunspot area coverage, comparable to the spot coverage of HAT-P-11 (Morris et al. 2017b). It is possible that the marginal detection of p₀ > p₁ is attributable to either or both planetary oblateness and occulted starspots.

Zoom In Zoom Out Reset image size

5.1.7. Kepler-412

Kepler-412 is a G3V host to a hot Jupiter with M_p = 0.939 ± 0.085M_J, and an apparently inflated radius of 1.325 ± 0.043R_J (Deleuil et al. 2014).

We fit the phase-folded Kepler light curve of Kepler-412 for p₀, p₁, b, t₀, T₁₄, M_⋆, R_⋆, and quadratic limb-darkening parameters. We place priors on M_⋆ and R_⋆ as described in Section 5.1.4. The results are shown in Figure 14; we find ${p}_{0}={R}_{p}/{R}_{\star }={0.0926}_{-0.0089}^{+0.0095}$ corresponding to ${R}_{p}=1.16\pm 0.11{R}_{J}$, consistent with the literature value (R_p/R_⋆ = 0.1058 ± 0.0023, Deleuil et al. 2014). We measure p₀ ≈ p₁.

Zoom In Zoom Out Reset image size

As with Kepler-39 in Section 5.1.6, p₀ ≲ p₁ could be interpreted as insignificant evidence (∼1σ) for dark starspots on the stellar photosphere outside of the transit chord; however, without the ability to further refine the uncertainty on p₀, we cannot strengthen this claim. The Kepler light curve shows small variations in the stellar intensity that may be rotational modulation due to unocculted starspots (see Figure 13).

5.2. K2 Observations of TRAPPIST-1

TRAPPIST-1 is an M8V host to seven Earth-sized planets (Gillon et al. 2016, 2017; Luger et al. 2017; Delrez et al. 2018). Its spots seem to evolve on a timescale similar to the apparent rotation period (Roettenbacher & Kane 2017), the spot- and faculae-covering fractions might be quite high (Rackham et al. 2018; Zhang et al. 2018), and bright spots might be required to explain the apparent rotational modulation of TRAPPIST-1 (Morris et al. 2018a). Here we analyze the K2/EVEREST short-cadence TRAPPIST-1 light curves of its two innermost planets for evidence of photospheric inhomogeneities (Luger et al. 2016; Luger 2017).

We fit the transit light curves of TRAPPIST-1 b and c for p₀, p₁, T₁₄ and the quadratic limb-darkening coefficients u₁ and u₂, see Figures 15 and 16. We place Gaussian priors on the impact parameter based on the joint light curve analysis by Luger et al. (2017), with impact parameters for planets b and c: ${b}_{{\rm{b}}}={0.093}_{-0.015}^{+0.011}$ and ${b}_{{\rm{c}}}={0.128}_{-0.020}^{+0.015}$.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

We find p₀ ≈ p₁ for both planets, indicating insufficient evidence for a difference in spot coverage inside compared to outside of the overlapping transit chords of planets b and c. Combined with the lack of observed spot occultations, the indication that the star may not be highly spotted is somewhat at odds with the spot-covering fraction estimates from Rackham et al. (2018) and Zhang et al. (2018), who find a potentially large spot-covering fraction, ${f}_{S}={8}_{-7}^{+18} \%$. As best we can tell from Doppler imaging, fully convective stars are likely highly spotted, and their spots may be randomly distributed, arranged into active latitudes, or concentrated at the poles (Barnes & Collier Cameron 2001; Donati et al. 2003; Morin et al. 2008). If we continue to measure p₀ ≈ p₁ with further transit observations of TRAPPIST-1, that may suggest that active regions on the star are small, low contrast, and/or uniformly distributed. It will be especially interesting to search for differences between p₀ and p₁ for the outer planets, which span a range of impact parameters, and thus a range of stellar latitudes. Upcoming Spitzer and JWST observations may improve this measurement, as the degeneracy between p₀ and the limb darkening is substantially diminished in the infrared, although the spot contrast is also diminished at longer wavelengths.

5.3. Spitzer Light Curves

We analyze two Spitzer light curves of interest. One is the transit of HD 80606 b, which is remarkable, among other reasons, for having a 12 hr transit observed at a very short cadence, providing us with exceptionally well-sampled transit ingress and egress. The other is GJ 1214: an M dwarf host to a transiting super-Earth.

5.3.1. HD 80606

HD 80606/HD 80607 is a wide, solar-type binary system with a massive Jovian planet orbiting the brighter component in an extremely eccentric (e = 0.93), misaligned orbit (Naef et al. 2001; Moutou et al. 2009; Winn et al. 2009a). We re-analyze warm Spitzer photometry of the ∼12 hr long transit observed at 4.5 μm by Hébrard et al. (2010) (see Figure 17).

Zoom In Zoom Out Reset image size

We fit the Spitzer transit light curve of HD 80606 b for p₀, p₁, b, t₀ and T₁₄, fixing the quadratic limb-darkening parameters u₁, u₂ = 0.0866, 0.1071 (Claret et al. 2013). We find p₀ < p₁ with 96% confidence, suggesting that either the planet may be occulting a relatively bright region of the stellar surface, or that we have to place a constraint upon the impact parameter. The transit light curve of HD 80606 shows evidence of at least one starspot occultation; perhaps unocculted starpsots are responsible for the tension between p₀ and p₁ (see Figure 17).

The maximum likelihood ${p}_{0}={R}_{p}/{R}_{\star }={0.053}_{-0.017}^{+0.025}$ in combination with the stellar radius from Hébrard et al. (2010) of 1.007 ± 0.024R_⊙ yields the planetary radius ${R}_{p}={0.51}_{-0.16}^{+0.26}{R}_{J}$, 2σ smaller than proposed by Hébrard et al. (2010) (R = 0.981R_J); they also measure a smaller impact parameter, b = 0.808 ± 0.007, than we measure, which accounts for this discrepancy.

The density of the star inferred by Hébrard et al. (2010) is ρ_* = 1.39 ± 0.07 g/cc, which is consistent with the value we infer from the Huber et al. (2013) relation that we derived above of ρ_*,Huber = 1.29 ± 0.11 g/cc. We conclude that if we had placed this density constraint as a prior on the stellar density, we would have obtained a smaller impact parameter, and hence a larger value of p₀ (see Figure 3) consistent with Hébrard et al. (2010).

5.3.2. GJ 1214

GJ 1214 is an M4.5 host to a transiting super-Earth (Charbonneau et al. 2009). The stellar activity of GJ 1214 has been studied extensively for its effect on the transmission spectrum of this potentially water-rich world (Fraine et al. 2013). Rotational modulation of the stellar flux is very limited, suggesting that either the star has few or small spots, or more likely that the spots are arranged in a nearly axisymmetric distribution (Berta et al. 2011; Narita et al. 2013). We re-analyze warm Spitzer 4.5 μm photometry of 13 transits of GJ 1214 b by Gillon et al. (2014) to verify that the spot distribution inside the transit chord is similar to the rest of the stellar surface.

We fit the Spitzer transit light curve of GJ 1214 for p₀, p₁, b, T₁₄ and fit for the quadratic limb-darkening parameters q₁ and q₂ (Kipping 2013), see Figure 18. The resulting constraint on p₀ is very weak and is consistent with p₁, suggesting an isotropic spot distribution, consistent with the conclusions of Berta et al. (2011) and Narita et al. (2013).

Zoom In Zoom Out Reset image size

We have investigated the prospects for robust measurement the radius ratios of planets using the ratio of the ingress duration to total transit duration, which should be less affected by contamination by starspots than the transit depth measurements. We then applied this to a sample of 10 stars to look for differences between the radius ratio measured from ingress (p₀) versus that measured from transit depth (p₁).

Given the probability measurements of p₀ < p₁ for the 10 stars in our study, we can ask the question of whether there is evidence that the probability sample is drawn from a uniform probability distribution. We sort the probabilities of p₀ < p₁ for the 10 stars in our study, and plot these versus a uniform probability distribution. Figure 19 shows the cumulative probability distribution of the sample versus the measured probabilities. If the distributions of p₀ and p₁ are statistically consistent for the entire sample, then we expect that 10 measured probabilities of p₀ < p₁ will be consistent with being drawn from a uniform probability distribution. We apply the Kolmogorov–Smirnov test to the sample, finding a maximum distance of −0.2 for a sample size of 10, giving a probability that this is drawn from a uniform distribution of 28%. We view this as indicating that the distribution of p₀ < p₁ probabilities is likely drawn from a uniform distribution; i.e., that the sample as a whole is consistent with p₀ = p₁ for all planets.

Zoom In Zoom Out Reset image size

Similar analyses have been conducted for the single systems CoRoT-2 (Bruno et al. 2016) and CoRoT-7 (Barros et al. 2014), and more general discussions appear in Oshagh et al. (2013) and Csizmadia et al. (2013). The main differences between this work and others is that we explicitly use the ingress and egress durations to measure the true planet radii in the presence of bright or dark regions on the stellar surface.

This work echoes Csizmadia et al. (2013); in particular, we found that fixing the limb-darkening parameters to their theoretical values for several systems introduced artificial constraints on the impact parameter and p₁, occasionally producing apparent discrepancies where ${p}_{0}\ne {p}_{1}$, which become consistent once the limb-darkening parameters are allowed to float. We encourage users of this light curve parameterization to fit for the limb-darkening parameters whenever possible, though we note the exceptionally good fit to TrES-2 using the quadratic limb-darkening parameters of Magic et al. (2015).

We also note the importance of asteroseismic constraints on the orbital parameters for several systems. The asteroseismic stellar density provides us with an independent measurement of a/R_⋆, which is otherwise degenerate with i_o, p₀ and the limb-darkening parameters. Bright TESS targets may also be amenable to asteroseismic density measurements, and therefore good candidates for this self-contamination analysis. Alternatively the stellar density can be measured to high precision in multi-planet systems from the planet periods and transit durations, which will be valuable for dim stars like TRAPPIST-1.

Diminished limb-darkening in the infrared promises that Spitzer and JWST observations of transiting exoplanets will be interesting subjects for analysis with the self-contamination analysis. Ground-based follow-up may also be a fruitful means of detecting the affects of stellar activity on transiting exoplanet light curves, especially with the high precision and time resolution enabled by holographic diffusers (see e.g., Stefansson et al. 2017; Morris et al. 2018b).

We have presented a reparameterization of the transit light curve of Mandel & Agol (2002) which splits the original “p” parameter into two parameters: p₀ = R_p/R_⋆ which defines the planet radius, and ${p}_{1}\approx \sqrt{\delta }$ which defines the transit depth. This parameterization allows the transit model to account for significant contamination by bright or dark active regions on the stellar surface, or significant planetary oblateness in the planet’s direction of motion. The resulting constraint on p₀ = R_p/R_⋆ is more accurate in the presence of stellar activity (and usually less precise).

We fit the light curves of several transiting planets to study the photospheric inhomogeneities of their host stars, see Table 1. We report p₀ ≈ p₁ (no significant detection of self-contamination) for Kepler light curves of TrES-2, HAT-P-7, TRAPPIST-1, and Spitzer observations of GJ 1214. We find that the uncertainties on p₀ are typically an order of magnitude larger than those on p₁, consistent with estimates of the noise (Appendix C). We find little evidence for transit depth dilution due to occulted starspots (p₀ > p₁) for the well-studied spotted pair of host stars HAT-P-11 and Kepler-17, and we find weak evidence that the transiting planets of Kepler-412 and HD 80606 likely occult relatively bright regions of the stellar photosphere (p₀ < p₁). We can recover the reported oblateness of Kepler-39 b using this parameterization, though its detection is not statistically significant. We note that in general the oblateness is likely degenerate with self-contamination, so the unusually large inferred oblateness may have an alternative explanation as being due to an inhomogeneous photosphere.

In the best cases we have studied in this paper, HAT-P-11b, Kepler-17b, and TrES-2b, we obtain sensitivity to self-contamination, at the 1%–3% level (Table 1), which is close enough to the expected levels of contamination that we were unable to achieve a definitive detection. This ratio of precisions on p₀ ranges from 5 to 25 times the uncertainties on p₁ (Table 1) The main advantage, then, in measuring p₀ is to obtain the radius ratio of the planet to the star when the unknown contamination of the stellar flux is significant. The other circumstance which may favor measuring p₀ is when there is significant red noise, which has a larger amplitude on the timescale of the transit than on the timescale of ingress/egress. Granulation noise tends to be strongly red, and thus will affect the measurement of the transit depth more strongly than the measurement of the ingress/egress duration.

With the JWST we expect to obtain much higher precision on p₀ due to the larger collecting area. As an example, the TRAPPIST-1 system has ingress/egress durations of ≈2–5 min, and when observed with NIRSPEC, we expect precisions of 2–5 s for the precision of these measurements. This will enable a measurement of p₀ comparable to the current precisions obtained with Spitzer for which multiple transits have been observed for each planet. Thus, we expect that the JWST will yield constraints upon p₀ which will give accurate radius ratios for these planets to diagnose the contamination by starspots. We find our simulations with extremely high S/N (Section 4) demonstrate that the radius ratio of the planet measured from p₀ can be recovered more accurately than that measured from p₁ in the presence of starspot contamination, since p₁ is biased by the presence of starspots (although p₁ is measured more precisely).

We have shown that p₀ is degenerate with the limb-darkening parameters. As a result, this technique will work better at red wavelengths, where limb-darkening is less severe, than in the blue. However, the contrast of starspots against the stellar photosphere diminishes as one observes at longer wavelengths as well, so this technique might be best suited to observations in the red optical, where the spot contrast may be significant but the limb darkening is weaker.

This technique is complementary to other starspot measurement techniques; it is sensitive to time-independent spots, though it provides a weaker signal than techniques like the flux deficit. The flux deficit technique, which measures variations in flux as a star rotates, has been applied to vast numbers of Kepler stars (Notsu et al. 2013; Walkowicz & Basri 2013; Mathur et al. 2014). Alternatively, spot distributions can be revealed by detailed modeling of individual spots throughout rotational modulation (Davenport et al. 2015), or via observations of spot occultations by transiting exoplanets (for example: Wolter et al. 2009; Sanchis-Ojeda & Winn 2011; Davenport 2015; Morris et al. 2017b; Dai et al. 2018).

We thank Laura Kreidberg, Ian Dobbs-Dixon, Travis Berger, and Dan Huber. We acknowledge support from NSF grant 1615315.

This research has made use of NASA’s Astrophysics Data System. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. This paper includes data collected by the Kepler mission. Funding for the Kepler mission is provided by the NASA Science Mission directorate. This paper includes data collected by the K2 mission. Funding for the K2 mission is provided by the NASA Science Mission directorate. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. This research has made use of the VizieR catalog access tool, CDS, Strasbourg, France. The original description of the VizieR service was published in A&AS 143, 23. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.

Facilities: Kepler - The Kepler Mission, K2 - , Spitzer - , ESA/Gaia. -

Software: batman (Kreidberg 2015), emcee (Foreman-Mackey et al. 2013), corner (Foreman-Mackey 2016), astropy (The Astropy Collaboration et al. 2018), ipython (Pérez & Granger 2007), numpy (Van Der Walt et al. 2011), scipy (Jones et al. 2001), matplotlib (Hunter 2007).

For a transiting exoplanet in a circular orbit, the transit duration from first through fourth contact is

$$\begin{eqnarray}&&{T}_{14}=\displaystyle \frac{P}{\pi }{\sin }^{-1}\left[\displaystyle \frac{{R}_{\star }}{a}\displaystyle \frac{\sqrt{{(1+{p}_{0})}^{2}-{b}^{2}}}{\sin i}\right],\end{eqnarray} \tag{ 26 }$$

and the duration from second through third contact is

$$\begin{eqnarray}&&{T}_{23}=\displaystyle \frac{P}{\pi }{\sin }^{-1}\left[\displaystyle \frac{{R}_{\star }}{a}\displaystyle \frac{\sqrt{{(1-{p}_{0})}^{2}-{b}^{2}}}{\sin i}\right],\end{eqnarray} \tag{ 27 }$$

where p₀ = R_p/R_⋆, P is the orbital period, b is the impact parameter, i is the planet’s orbital inclination, and a/R_⋆ is the scaled orbital semimajor axis (Winn 2010). We can invert these relations to find the planet-to-stellar radius ratio as a function of the transit durations,

$$\begin{eqnarray}\displaystyle \frac{{R}_{p}}{{R}_{\star }} & = & \displaystyle \frac{1}{2}\left({\left[{\left[\displaystyle \frac{a}{{R}_{\star }}\sin \displaystyle \frac{\pi {T}_{14}}{P}\sin i\right]}^{2}+{b}^{2}\right]}^{1/2}\right.\\ & & \left.-\,{\left[{\left[\displaystyle \frac{a}{{R}_{\star }}\sin \displaystyle \frac{\pi {T}_{23}}{P}\sin i\right]}^{2}+{b}^{2}\right]}^{1/2}\right).\end{eqnarray} \tag{ 28 }$$

We can get a sense for the scaling of the terms in this equation by simplifying to the case where i = 90°, b = 0 and ${T}_{14},{T}_{23}\ll P$ using the small-angle approximation,

$$\begin{eqnarray}&&\displaystyle \frac{{R}_{p}}{{R}_{\star }}\sim \displaystyle \frac{\pi }{2P}\displaystyle \frac{a}{{R}_{\star }}({T}_{14}-{T}_{23}).\end{eqnarray} \tag{ 29 }$$

The constraint on the planetary radius (p₀ = R_p/R_⋆ in our reparameterization) primarily comes from the difference between the durations of first through fourth contact and second through third contact.

In Sections 4.1 and 4.2 we assumed that the starspots had the same contrast as sunspots, c = 0.7. In this section, we revisit those toy-model analyses with more extreme spot contrasts, by setting the contrast to that of sunspot umbrae, c = 0.2.

First we simulate a dense band of spots with contrast c = 0.2 centered on the stellar equator; see Figure 20. The self-contamination parameter $\epsilon =1-{({p}_{1}/{p}_{0})}^{2}=-{0.598}_{-0.032}^{+0.014}$ in this limiting case.

Zoom In Zoom Out Reset image size

Next we simulate a pair of polar spots that extend almost all the way from the pole to the edge of the transit chord, with contrast c = 0.2; see Figure 21. The self-contamination parameter $\epsilon ={0.419}_{-0.015}^{+0.011}$ in this case.

Zoom In Zoom Out Reset image size

Thus one might expect to vary roughly on −0.5 ≲  ≲ 0.5 for extreme self-contamination due to occulted or unocculted starspots.

Using the estimates of Carter et al. (2008) for the uncertainties on the ingress and total duration given Fisher information analysis of a piecewise-linear transit model, we can estimate the uncertainties on p₀ and p₁. For flux observations with independent Gaussian uncertainties σ, for a transit with depth δ, ingress duration τ and mid-ingress to mid-egress duration T are defined as

$$\begin{eqnarray}&&T\equiv 2{\tau }_{0}\sqrt{1-{b}^{2}}\end{eqnarray} \tag{ 30 }$$

$$\begin{eqnarray}&&\tau \equiv 2{\tau }_{0}\displaystyle \frac{{p}_{0}}{\sqrt{1-{b}^{2}}}\end{eqnarray} \tag{ 31 }$$

where τ₀ is

$$\begin{eqnarray}&&{\tau }_{0}=\displaystyle \frac{P}{2\pi }\displaystyle \frac{{R}_{\star }}{a},\end{eqnarray} \tag{ 32 }$$

with uncertainties on τ and T given by

$$\begin{eqnarray}&&{\sigma }_{\tau }\approx \displaystyle \frac{\sigma }{\delta T}\sqrt{\displaystyle \frac{6\tau }{{\rm{\Gamma }}}},\end{eqnarray} \tag{ 33 }$$

$$\begin{eqnarray}&&{\sigma }_{T}\approx \displaystyle \frac{\sigma }{\delta T}\sqrt{\displaystyle \frac{2\tau }{{\rm{\Gamma }}}},\end{eqnarray} \tag{ 34 }$$

where Γ is the sampling rate (if N photometric measurements are taken uniformly over a total observing time T₀, then Γ = N/T₀), so Γ⁻¹ is the time between the start of successive exposures. Rearranging, we find

$$\begin{eqnarray}&&{p}_{0}=\displaystyle \frac{\tau T}{4{\tau }_{0}^{2}},\end{eqnarray} \tag{ 35 }$$

and therefore the uncertainty, ${\sigma }_{{p}_{0}}$, is given by

$$\begin{eqnarray}&&{\left(\displaystyle \frac{{\sigma }_{{p}_{0}}}{{p}_{0}}\right)}^{2}=\displaystyle \frac{T}{{Q}^{2}}\left[\displaystyle \frac{6+\eta }{\tau }\right]+{\left(\displaystyle \frac{{\sigma }_{{\tau }_{0}}}{{\tau }_{0}}\right)}^{2}\end{eqnarray} \tag{ 36 }$$

in the limit of $\tau \ll T$, where $\eta =T/({T}_{0}-T-\tau )$ is the ratio of the duration of photometric measurements in-transit to out-of-transit ($\eta \to 0$ for perfectly known out-of-transit flux). From this equation we see conclusions we discussed elsewhere in this work; for example, if τ₀ is known imprecisely by lack of prior constraints on the stellar density or transit impact parameter, then p₀ will have large uncertainties.

If we know the stellar density/impact parameter well (${\sigma }_{{\tau }_{0}}\to 0$) and measure the out-of-transit flux well ($\eta \to 0$), then

$$\begin{eqnarray}&&\displaystyle \frac{{\sigma }_{{p}_{0}}}{{p}_{0}}=\displaystyle \frac{\sigma {6}^{1/2}}{{p}_{1}^{2}{({\rm{\Gamma }}\tau )}^{1/2}}\propto \displaystyle \frac{{(1-{b}^{2})}^{1/4}}{{p}_{0}^{1/2}},\end{eqnarray} \tag{ 37 }$$

i.e., we obtain higher precision on p₀ for systems with higher impact parameters, for which the ingress/egress durations are longer.

The uncertainty on p₁ can be computed from σ_δ given ${p}_{1}^{2}\approx \delta$, so

$$\begin{eqnarray}&&{\sigma }_{{p}_{1}}=\displaystyle \frac{{\sigma }_{{p}_{1}^{2}}}{2{p}_{1}}\end{eqnarray} \tag{ 38 }$$

thus

$$\begin{eqnarray}&&\displaystyle \frac{{\sigma }_{{p}_{1}}}{{p}_{1}}=\displaystyle \frac{\sigma }{2{p}_{1}^{2}{({\rm{\Gamma }}T)}^{1/2}}.\end{eqnarray} \tag{ 39 }$$

Comparing the fractional uncertainties on p₀ (Equation (37)) and p₁ (Equation (39)), we find:

$$\begin{eqnarray}&&\displaystyle \frac{{\sigma }_{{p}_{0}}}{{p}_{0}}{\left(\displaystyle \frac{{\sigma }_{{p}_{1}}}{{p}_{1}}\right)}^{-1}={24}^{1/2}{\left(\displaystyle \frac{T}{\tau }\right)}^{1/2}=15.5{(1-{b}^{2})}^{1/2}{({p}_{0}/0.1)}^{-1/2}.\end{eqnarray} \tag{ 40 }$$

Consequently, the fractional uncertainty on p₀ tends to be ≈  an order of magnitude larger than p₁; this can be exacerbated further by strong limb -darkening which causes the depth of transit at ingress and egress to be shallower than the mean transit depth.

The foregoing equations assume uncorrelated, time-independent white noise, which will not be the case for high-precision measurements, at which point the uncertainties will be dominated by stellar granulation variability.