ACM竞赛全攻略：模板与算法汇总

原创于 2025-05-28 13:45:41 发布 · 954 阅读

CC 4.0 BY-SA版权

简介：这份资源集合为ACM（国际大学生程序设计竞赛）参赛者提供了编程模板、算法总结、比赛知识和训练策略。包括但不限于数据结构操作、常用算法实现和输入输出优化的模板，以及搜索算法、动态规划、贪心算法、回溯法、分治法等算法的流程图。此外，还包括ACM比赛规则、团队协作要领和时间空间复杂度的优化。参与者可以通过刷题、强化数据结构和算法基础、提升编程语言熟练度来准备ACM竞赛。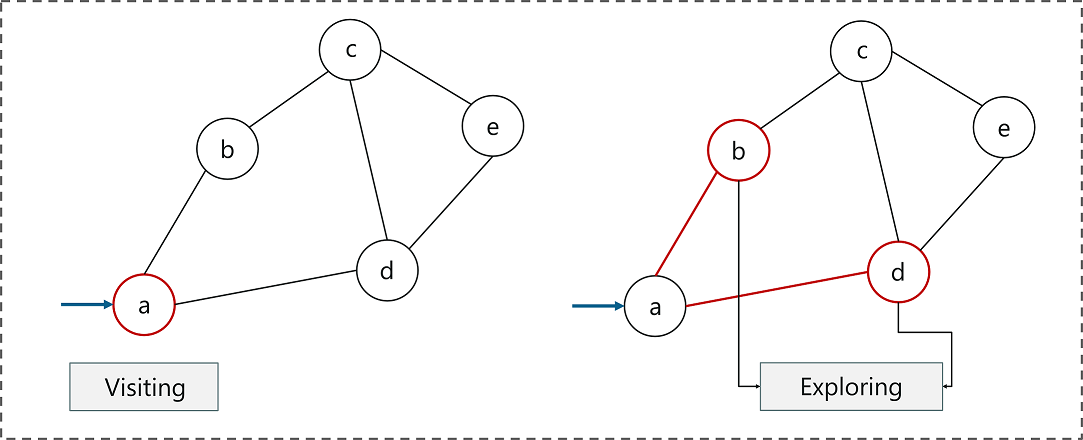

1. ACM编程模板应用

ACM编程模板作为提高编程效率和保证代码质量的重要工具，已成为许多计算机竞赛和日常开发中的首选。在深入研究算法和数据结构之前，熟悉和掌握一些基本的编程模板能够帮助我们快速搭建起解题框架，减少不必要的调试时间。

1.1 编程模板的基本概念

编程模板是一套事先定义好的代码段，用于处理特定类型的编程问题。它通常包含了算法实现的核心逻辑、数据结构的定义以及辅助函数等。在ACM竞赛中，合理地运用模板不仅可以提升编码效率，还能确保代码的可读性和可维护性。

1.2 模板的分类与选择

模板可以根据不同的应用场景进行分类，例如：字符串处理、图的遍历、数论等。选择合适的模板可以简化编程过程，提高问题求解的速度。例如，在处理图的广度优先搜索（BFS）时，我们可以直接套用现成的BFS模板，只需修改相应的邻接表和访问标记即可。

1.3 模板在实际应用中的优化

模板的使用并不意味着完全的复制粘贴。在实际应用中，我们常常需要根据具体问题对模板进行适当的调整和优化。例如，调整数据结构以适应问题规模，或者优化算法细节以应对更复杂的情况。在这一过程中，我们不仅要学会灵活运用模板，还要不断深化对模板背后算法原理的理解。

2. 算法基础与应用技巧

在探讨算法这一领域时，我们通常着眼于算法的设计原理、实现方式以及在解决特定问题时的应用技巧。本章将深入探讨搜索算法、动态规划以及贪心算法这三种基础算法，并通过实例和代码示例来展示它们的实际应用场景。

2.1 搜索算法的探索与实现

搜索算法是算法设计中的一种基本类型，主要用途是检索一系列数据中的元素。在这一部分中，我们将深入分析两种搜索算法：深度优先搜索（DFS）和广度优先搜索（BFS），以及它们在解决搜索问题时的优势和局限性。

2.1.1 深度优先搜索(DFS)的原理与应用

深度优先搜索是一种用于遍历或搜索树或图的算法。在 DFS 中，算法尽可能沿着树的分支深入到某个节点的叶子节点，然后再回溯到前一个节点，重复此过程直到所有节点都被访问过。

原理：在 DFS 的实现中，通常采用递归或者栈的结构来记录路径，从而保证每次都能访问到下一个节点的未被访问过的分支。

应用：深度优先搜索广泛应用于解决迷宫问题、有向图/无向图的路径问题以及拓扑排序等。

2.1.2 广度优先搜索(BFS)的原理与应用

与深度优先搜索不同，广度优先搜索从根节点开始，逐步探索每个分支，直到所有的节点都被访问过为止。其特点是从根节点开始逐层向外扩展。

原理： BFS 使用队列来记录节点访问的顺序，确保每次扩展的是当前层的节点。

应用： BFS 适合解决最短路径问题，例如在无权图中寻找两点之间的最短路径，以及层序遍历等。

示例代码：DFS 和 BFS 的实现

# DFS 递归实现
def dfs_recursive(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start)
    for next in graph[start] - visited:
        dfs_recursive(graph, next, visited)
    return visited

# BFS 迭代实现
from collections import deque

def bfs_iterative(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        vertex = queue.popleft()
        if vertex not in visited:
            visited.add(vertex)
            print(vertex)
            queue.extend(set(graph[vertex]) - visited)
    return visited

# 示例图
graph = {'A': set(['B', 'C']),
         'B': set(['A', 'D', 'E']),
         'C': set(['A', 'F']),
         'D': set(['B']),
         'E': set(['B', 'F']),
         'F': set(['C', 'E'])}

# 执行 DFS 和 BFS
dfs_result = dfs_recursive(graph, 'A')
print("DFS:", dfs_result)
bfs_result = bfs_iterative(graph, 'A')
print("BFS:", bfs_result)

在此代码段中，我们实现了图的深度优先搜索和广度优先搜索。 dfs_recursive 函数展示了递归方式的 DFS 实现，而 bfs_iterative 函数则展示了使用队列进行迭代的 BFS 实现。每访问一个节点，我们将其加入到已访问集合 visited 中，并输出节点值。

2.2 动态规划的理论与实践

动态规划是解决具有重叠子问题和最优子结构特性问题的一类算法。动态规划算法将复杂问题分解为简单子问题，并通过存储子问题的解以避免重复计算。

2.2.1 动态规划的基本原理

动态规划通常涉及三个基本要素：最优子结构、重叠子问题和状态转移方程。

最优子结构 指的是问题的最优解包含其子问题的最优解。
重叠子问题 是指在递归过程中相同的子问题会被多次计算。
状态转移方程 是描述问题状态之间如何转换的一组方程。

2.2.2 动态规划的常见应用实例

动态规划在诸如背包问题、最长公共子序列、编辑距离等领域有着广泛的应用。

示例代码：背包问题的动态规划实现

# 0-1背包问题，使用动态规划求解
def knapsack(values, weights, capacity):
    n = len(values)
    # dp[i][w] 表示考虑前i个物品，当前背包容量为w时，可以达到的最大价值
    dp = [[0 for _ in range(capacity + 1)] for _ in range(n + 1)]

    for i in range(1, n + 1):
        for w in range(1, capacity + 1):
            if weights[i - 1] <= w:
                # 如果第i个物品可以装入背包
                dp[i][w] = max(dp[i - 1][w], dp[i - 1][w - weights[i - 1]] + values[i - 1])
            else:
                # 如果第i个物品不能装入背包
                dp[i][w] = dp[i - 1][w]

    return dp[n][capacity]

values = [60, 100, 120]
weights = [10, 20, 30]
capacity = 50

max_value = knapsack(values, weights, capacity)
print("Max value in knapsack:", max_value)

在这段代码中，我们定义了一个函数 knapsack ，它实现了一个典型的动态规划问题——0-1背包问题。我们建立了一个二维数组 dp ，用来保存子问题的解。通过迭代计算每个子问题的最优解，最终得到背包问题的最大价值。

2.3 贪心算法的深入解析

贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。

2.3.1 贪心算法的原理及适用场景

贪心算法通常用于问题可以分解为多个子问题，每个子问题求解方法相同，并且每个子问题的最优解能导致全局最优解的场景。

2.3.2 贪心算法的实例分析

贪心算法适用于解决一些如最小生成树、哈夫曼编码、活动选择问题等，这些场景中可以通过局部最优的选择来达到全局最优。

示例代码：找零问题的贪心算法实现

# 贪心算法求解找零问题
def min_coins(coins, amount):
    # 对硬币种类进行排序，贪心算法中通常需要对输入进行排序
    coins.sort(reverse=True)
    # 初始化
    count = 0
    for coin in coins:
        while amount >= coin:
            amount -= coin
            count += 1
    return count if amount == 0 else -1

coins = [1, 5, 10, 25]
amount = 63

min_coins_count = min_coins(coins, amount)
print("Minimum coins required:", min_coins_count)

在上述示例中， min_coins 函数尝试以贪心的方式解决找零问题。我们先将硬币种类按价值从大到小排序，然后从价值最大的硬币开始，尽可能多地使用当前硬币种类进行找零，直到总金额为零。

在本章节中，我们探讨了搜索算法、动态规划以及贪心算法这三种基础算法，并且通过实例和代码演示了它们的应用技巧。下一部分我们将继续深入，探讨复杂问题的解决方法论。

3. 复杂问题解决方法论

在面对复杂的编程挑战时，传统直接的编程方法往往难以奏效。第三章“复杂问题解决方法论”致力于探讨和掌握解决复杂问题的有效策略和方法。本章将深入分析回溯法和分治法，这两种解决复杂问题的重要算法思想，它们在算法设计中具有重要的地位，尤其是在求解约束满足问题、最优化问题中发挥着关键作用。

3.1 回溯法的策略与应用

3.1.1 回溯法的问题解决框架

回溯法是一种通过递归来遍历解空间，并通过剪枝来避免无效搜索的算法策略。它在解决组合问题，如排列、组合和子集问题中非常有效。回溯法通常包括以下几个基本步骤：

选择：从一个可能的解开始，逐步增加解的成分。
可行性判断 ：检查当前的解是否满足问题的约束条件。
递归搜索 ：如果当前的解满足约束，则进一步扩展解。
回溯：如果当前的解不满足约束条件或已经找到一个解，撤销上一步的决策，回退到上一个状态。

下面是一个经典回溯问题的伪代码框架：

def backtrack(路径, 选择列表):
    if 满足结束条件:
        结果.append(路径)
        return

    for 选择 in 选择列表:
        做出选择
        if 可行(路径, 选择):
            backtrack(路径, 选择列表)
        撤销选择

3.1.2 常见回溯问题的求解示例

以经典的N皇后问题为例，问题要求在一个N×N的棋盘上放置N个皇后，使得它们不能相互攻击。即任意两个皇后不能处在同一行、同一列或同一斜线上。

以下是使用Python实现的一个N皇后问题的解决方案：

def solve_n_queens(n):
    def is_valid(board, row, col):
        # 检查同一列是否有皇后互相冲突
        for i in range(row):
            if board[i] == col or \
               board[i] - i == col - row or \
               board[i] + i == col + row:
                return False
        return True

    def solve(board, row):
        if row == n:
            result.append(board[:])
            return
        for col in range(n):
            if is_valid(board, row, col):
                board[row] = col
                solve(board, row + 1)
                board[row] = -1  # 回溯

    result = []
    solve([-1] * n, 0)
    return result

# 打印所有的解
solutions = solve_n_queens(4)
for solution in solutions:
    for row in solution:
        print(" ".join("Q" if col == row else "." for col in range(len(solution))))
    print()

在这个问题中，我们使用了一个一维数组 board 来表示棋盘，其中 board[i] = j 表示第 i 行的皇后放置在第 j 列。每放置一个皇后，都会调用 solve 函数尝试放置下一个皇后。如果当前行无法放置皇后，则回溯到上一行，并尝试其他列。

3.2 分治法的核心思想与算法实现

3.2.1 分治法的基本原理

分治法是一种分而治之的思想，即将原问题分解为若干个规模较小但类似于原问题的子问题，递归解决这些子问题，然后合并其结果以得到原问题的解。分治法的三个基本步骤是：

分解：将原问题分解为若干个规模较小的同类问题。
解决：递归求解各个子问题。如果子问题足够小，则直接求解。
合并：将子问题的解合并为原问题的解。

分治法的效率依赖于如何分解问题以及如何有效地合并结果。通常情况下，分解应当尽量简单且子问题之间相互独立，而合并则需要高效的算法来确保整体的高性能。

3.2.2 分治法的经典算法案例

3.2.2.1 归并排序

归并排序是一种典型的分治法应用。其基本思想是将数组分成两半，分别进行排序，然后将排序好的两半合并在一起。合并的过程需要一个额外的数组，用于存放合并后的结果。

下面是使用Python实现的归并排序算法：

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    return merge(left, right)

def merge(left, right):
    merged = []
    l, r = 0, 0
    while l < len(left) and r < len(right):
        if left[l] <= right[r]:
            merged.append(left[l])
            l += 1
        else:
            merged.append(right[r])
            r += 1
    merged.extend(left[l:])
    merged.extend(right[r:])
    return merged

# 示例数组
array = [3, 1, 4, 1, 5, 9, 2, 6, 5]
sorted_array = merge_sort(array)
print(sorted_array)

上述代码中， merge_sort 函数是递归的主要部分，负责数组的分解。而 merge 函数则是合并阶段的核心，它将两个已排序的数组合并为一个。

归并排序算法的时间复杂度为O(n log n)，它适用于对大数据集合进行排序。在合并过程中，由于是有序数组，可以保证每次合并都是线性的操作。

3.2.2.2 快速排序

快速排序是另一种广泛使用的分治法排序算法。它的基本思想是在数组中选择一个元素作为“基准”，重新排列数组，使得所有元素小于基准的都在它的左边，所有元素大于基准的都在它的右边。然后递归地排序基准左右两边的子数组。

快速排序通常比归并排序有更高的效率，尤其在处理大数据集时，它的时间复杂度期望值也是O(n log n)，但其常数因子较小。

快速排序的Python实现如下：

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

# 示例数组
array = [3, 1, 4, 1, 5, 9, 2, 6, 5]
sorted_array = quick_sort(array)
print(sorted_array)

以上快速排序实现的核心在于 quick_sort 函数，它选取数组中间的元素作为基准，然后通过列表推导式将数组分为三部分：小于基准的元素、等于基准的元素和大于基准的元素。

总结起来，分治法是解决复杂问题的一种强有力的工具。理解分治法的基本原理，并熟悉其在算法中的应用，对解决实际问题至关重要。通过回溯法和分治法的学习，我们能够掌握解决复杂问题的多种思路，进一步提升编程技能。

4. ACM竞赛与团队合作

4.1 ACM竞赛规则的全面解读

4.1.1 竞赛规则要点分析

ACM国际大学生程序设计竞赛（ACM-ICPC）是业界公认的最权威、最热门的计算机竞赛之一。它不仅考察参赛者对算法和编程语言的掌握，还考验团队协作和问题解决能力。

ACM竞赛的主要规则包括：

团队组成： 每个团队由3名队员组成，队员应为在校大学生，每人仅能代表一个学校参加竞赛。
语言和工具： 参赛队伍需使用C、C++或Java等语言编程，不允许使用外部库和预处理宏定义。
题目类型： 竞赛题目通常包含算法、数学、逻辑推理等，对参赛者的综合能力要求很高。
时间限制： 每场预赛通常为5个小时，包括读题、讨论和编写代码等环节。
提交与测评： 参赛队伍需要在计算机上编写代码并通过系统的编译和测试。提交后的程序将与一系列测试用例进行对比，只有正确解答所有测试用例的程序才被认为是正确的。