Stacking X-Ray Observations of “Little Red Dots”: Implications for Their Active Galactic Nucleus Properties

Minghao Yue; Anna-Christina Eilers; Tonima Tasnim Ananna; Christos Panagiotou; Erin Kara; Takamitsu Miyaji

doi:10.3847/2041-8213/ad7eba

1. Introduction

The recent launch of the James Webb Space Telescope (JWST) has opened new windows into studies of distant galaxies and supermassive black holes (SMBHs). One particularly exciting discovery by JWST is the abundant population of so-called “little red dots” (LRDs). LRDs are compact objects at z ≳ 4 with very red near-infrared color, which have been found by many JWST survey programs (e.g., J. E. Greene et al. 2024; Y. Harikane et al. 2023; D. D. Kocevski et al. 2023; I. Labbe et al. 2023; J. Matthee et al. 2024). Their spectra exhibit broad Hα emission lines, suggesting type I active galactic nuclei (AGN) activity in their cores. The number density of LRDs at z ∼ 5 is about 10⁻⁵–10⁻⁴ Mpc⁻³ mag⁻¹ (e.g., J. E. Greene et al. 2024), which is close to the entire X-ray AGN population at similar redshifts, and is ∼1–2 dex higher than the faint end of quasar luminosity functions (e.g., Y. Matsuoka et al. 2018; J.-T. Schindler et al. 2023). This comparison suggests that LRDs might be a population of previously unexplored dust-reddened AGNs and that our current picture of SMBH–galaxy coevolution might be incomplete.

However, the properties of LRDs are still largely unclear, and a few models have been proposed to explain the observed features of these objects. D. D. Kocevski et al. (2023) found that the spectral energy distributions (SEDs) of LRDs can be explained either by a dust-obscured AGN plus a blue galaxy or by an unobscured AGN combined with a red galaxy. I. Labbe et al. (2023) and J. E. Greene et al. (2024) suggested that LRDs might be heavily obscured AGNs and that the broad emission lines and rest-frame UV continuum of LRDs might arise from the scattered light of the central AGNs. J. Matthee et al. (2024) proposed that LRDs represent a transition phase from heavily obscured AGNs to unobscured quasars. This model is in line with A. Noboriguchi et al. (2023), who found that LRDs share similar features with blue-excess dust-obscured galaxies (BluDOGs) at lower redshifts.

Nevertheless, type I AGNs are not the only plausible scenario that can explain the observational features of LRDs. Strong outflows in compact regions, likely driven by supernovae or star formation, can also generate broad Hα emission lines. This possibility has been discussed in, e.g., J. Matthee et al. (2024). J. F. W. Baggen et al. (2024) proposed that the broad lines of LRDs can be explained by the high central densities of these compact objects. Nevertheless, most spectroscopically observed LRDs show narrow unresolved forbidden lines (like [O iii]), which make it hard to explain the broad Hα lines purely with galactic-scale outflows (e.g., R. Maiolino et al. 2024).

All these uncertainties prevent us from further understanding the properties of LRDs and their implications on galaxy evolution models. Confirming the nature of LRDs requires multiwavelength observations that can unambiguously reveal signs of AGN activity. Some efforts have been carried out using the Mid-Infrared Instrument (MIRI) on JWST, aiming at detecting the hot dust emission heated by the AGN. For example, P. G. Pérez-González et al. (2024) analyzed the NIRCam and MIRI observations of 31 photometrically selected LRDs and performed SED fitting to test the AGN hypothesis. The authors found that the mid-infrared emissions of the LRDs are inconsistent with an AGN dust torus, potentially indicating that the SEDs of LRDs might not be AGN dominated.

X-ray emission is one of the most reliable indicators of AGN activity. Several studies have investigated the X-ray emission of LRDs in the Chandra deep fields (e.g., J. Lyu et al. 2024; J. Matthee et al. 2024), which reported nondetections for all the LRDs in their sample. B. Wang et al. (2024) reported a luminous LRD at z = 3.1 with an X-ray flux upper limit that is ∼100 times weaker than the expectation from its optical luminosity. K. Inayoshi & K. Ichikawa (2024) indicate that current X-ray observations are not deep enough to detect the X-ray emission for most individual LRDs. Meanwhile, D. D. Kocevski et al. (2024) recently discovered two bright photometrically selected LRDs detected in Chandra deep fields, which have L_X(2–10 keV) ∼ 10⁴⁴ erg s⁻¹ and N_H ∼ 10²³ cm⁻². The diverse results demonstrate that our knowledge about the X-ray properties of LRDs are still highly limited.

Since most spectroscopically confirmed LRDs do not have X-ray detections, a stacking analysis offers a viable way to investigate the X-ray properties of these objects. In this Letter, we aim to detect or put more stringent constraints on the X-ray fluxes of LRDs by stacking archival Chandra observations. We describe our sample and the stacking procedure in Section 2. The results are presented in Section 3. We discuss the implication of our results in Section 4 and conclude in Section 5. We adopt a flat ΛCDM cosmology with H₀ = 70 km s⁻¹ Mpc⁻¹ and Ω_M = 0.3.

2. Stacking the Chandra Observations of LRDs

2.1. Sample Selection

The aim of this study is to investigate the AGN hypothesis of LRDs. Therefore, our sample consists of spectroscopically confirmed LRDs that show broad Hα emission lines. We notice that some previous studies reported photometrically selected LRDs (e.g., C. C. Williams et al. 2024; V. Kokorev et al. 2024) and discussed their properties; however, these objects lack spectroscopic confirmation, and we do not include these objects in our analysis.

Specifically, we construct our sample by selecting broad Hα emitters (with FWHM_Hα > 1000 km s⁻¹) discovered by JWST NIRCam grism or NIRSpec observations by the time of the writing of this Letter. We further require that the targets should fall in one of the following Chandra deep fields: COSMOS (F. Civano et al. 2016), CDF-N (W. N. Brandt et al. 2001), CDF-S (P. Rosati et al. 2002), AEGIS (E. S. Laird et al. 2009), and X-UDS (D. D. Kocevski et al. 2018). This choice is made because the X-ray stacking software we use, CSTACK (T. Miyaji & R. E. Griffiths 2008), is currently only implemented to work on ACIS-I observations in Chandra deep fields. Objects in lensing cluster fields (e.g., those in J. E. Greene et al. 2024) are not covered by the database of CSTACK and are thus not included in our sample. Since these objects might suffer contamination from the X-ray emission of the foreground galaxy cluster, excluding these objects also avoids possible systematic uncertainties due to imperfect background subtraction.

During the stacking process (Section 2.2), we further exclude five objects with close companions or uneven background by visual inspection for which the background subtraction might be inaccurate. The final sample of this work consists of 34 objects from R. Maiolino et al. (2023), Y. Harikane et al. (2023), J. Matthee et al. (2024), and D. D. Kocevski et al. (2024). All the information about these objects is summarized in Table 1.

Table 1. The LRD Sample for Stacking

Name	R.A.	Decl.	Redshift	$\mathrm{log}{L}_{{\rm{H}}\alpha }$	FWHM_Hα	$\mathrm{log}{M}_{\mathrm{BH}}$ ^a	References ^b
	(deg)	(deg)		(erg s⁻¹)	km s⁻¹	(M_⊙)
CEERS-00397	214.83621	52.88269	6.000	${42.41}_{-0.07}^{+0.12}$	${1739}_{-317}^{+359}$	${7.00}_{-0.30}^{+0.26}$	Y. Harikane et al. (2023)
CEERS-00672^c	214.88967	52.83297	5.666	${43.26}_{-0.05}^{+0.05}$	${2208}_{-241}^{+277}$	${7.70}_{-0.13}^{+0.13}$	Y. Harikane et al. (2023)
CEERS-00717	215.08142	52.97219	6.936	${42.08}_{-0.08}^{+0.10}$	${6279}_{-881}^{+805}$	${7.99}_{-0.17}^{+0.16}$	Y. Harikane et al. (2023)
CEERS-00746^c	214.80912	52.86847	5.624	${43.83}_{-0.03}^{+0.02}$	${1660}_{-162}^{+157}$	${7.76}_{-0.11}^{+0.10}$	Y. Harikane et al. (2023)
CEERS-01236	215.14529	52.96728	4.484	${41.68}_{-0.08}^{+0.09}$	${3521}_{-485}^{+649}$	${7.26}_{-0.18}^{+0.19}$	Y. Harikane et al. (2023)
CEERS-01244	215.24067	53.03606	4.478	${42.89}_{-0.01}^{+0.01}$	${2228}_{-52}^{+75}$	${7.51}_{-0.03}^{+0.04}$	Y. Harikane et al. (2023)
CEERS-01665	215.17821	53.05936	4.483	${42.83}_{-0.04}^{+0.05}$	${1794}_{-171}^{+282}$	${7.28}_{-0.13}^{+0.15}$	Y. Harikane et al. (2023)
CEERS-02782	214.82346	52.83028	5.241	${42.88}_{-0.04}^{+0.04}$	${2534}_{-266}^{+260}$	${7.62}_{-0.12}^{+0.11}$	Y. Harikane et al. (2023)
GOODS-N-13733	189.05708	62.26894	5.236	${42.38}_{-0.04}^{+0.03}$	${2208}_{-200}^{+200}$	${7.49}_{-0.10}^{+0.10}$	J. Matthee et al. (2024)
GOODS-N-16813	189.17929	62.29253	5.355	${42.65}_{-0.05}^{+0.05}$	${2033}_{-219}^{+219}$	${7.55}_{-0.12}^{+0.12}$	J. Matthee et al. (2024)
GOODS-N-4014	189.30013	62.21204	5.228	${42.66}_{-0.02}^{+0.02}$	${2103}_{-159}^{+159}$	${7.58}_{-0.08}^{+0.08}$	J. Matthee et al. (2024)
GOODS-S-13971	53.13858	−27.79025	5.481	${42.40}_{-0.10}^{+0.08}$	${2192}_{-479}^{+479}$	${7.49}_{-0.25}^{+0.25}$	J. Matthee et al. (2024)
M23-10013704-2^c	53.12654	−27.81809	5.919	${41.99}_{-0.04}^{+0.03}$	${2416}_{-156}^{+179}$	${7.50}_{-0.31}^{+0.31}$	R. Maiolino et al. (2023)
M23-20621	189.12252	62.29285	4.681	${42.00}_{-0.03}^{+0.03}$	${1638}_{-150}^{+148}$	${7.30}_{-0.31}^{+0.31}$	R. Maiolino et al. (2023)
M23-3608	189.11794	62.23552	5.269	${41.46}_{-0.09}^{+0.10}$	${1373}_{-198}^{+361}$	${6.82}_{-0.33}^{+0.38}$	R. Maiolino et al. (2023)
M23-53757-2	189.26978	62.19421	4.448	${42.03}_{-0.04}^{+0.04}$	${2416}_{-157}^{+179}$	${7.69}_{-0.31}^{+0.32}$	R. Maiolino et al. (2023)
M23-73488-2	189.19740	62.17723	4.133	${42.52}_{-0.01}^{+0.01}$	${2160}_{-46}^{+45}$	${7.71}_{-0.30}^{+0.30}$	R. Maiolino et al. (2023)
M23-77652	189.29323	62.19900	5.229	${42.09}_{-0.04}^{+0.02}$	${1070}_{-180}^{+219}$	${6.86}_{-0.34}^{+0.35}$	R. Maiolino et al. (2023)
M23-8083	53.13284	−27.80186	4.648	${41.92}_{-0.02}^{+0.02}$	${1648}_{-130}^{+127}$	${7.25}_{-0.31}^{+0.31}$	R. Maiolino et al. (2023)
CEERS-5760^c	214.97244	52.96220	5.079	${41.81}_{-0.15}^{+0.15}$	${1800}_{-300}^{+300}$	${6.72}_{-0.17}^{+0.17}$	D. D. Kocevski et al. (2024)
CEERS-6126^c	214.92338	52.92559	5.288	${42.76}_{-0.03}^{+0.03}$	${1670}_{-60}^{+60}$	${7.18}_{-0.03}^{+0.03}$	D. D. Kocevski et al. (2024)
CEERS-7902^c	214.88680	52.85538	6.986	${43.20}_{-0.07}^{+0.07}$	${4180}_{-220}^{+220}$	${8.24}_{-0.06}^{+0.06}$	D. D. Kocevski et al. (2024)
CEERS-10444^c	214.79537	52.78885	6.687	${43.38}_{-0.06}^{+0.06}$	${5420}_{-370}^{+370}$	${8.57}_{-0.07}^{+0.07}$	D. D. Kocevski et al. (2024)
CEERS-13135^c	214.99098	52.91652	4.955	${42.98}_{-0.03}^{+0.03}$	${1850}_{-50}^{+50}$	${7.39}_{-0.03}^{+0.03}$	D. D. Kocevski et al. (2024)
CEERS-13318^c	214.98304	52.95601	5.280	${43.77}_{-0.05}^{+0.05}$	${3300}_{-60}^{+60}$	${8.34}_{-0.03}^{+0.03}$	D. D. Kocevski et al. (2024)
CEERS-14949^c	215.13706	52.98856	5.684	${42.50}_{-0.08}^{+0.08}$	${1520}_{-115}^{+115}$	${6.95}_{-0.08}^{+0.08}$	D. D. Kocevski et al. (2024)
CEERS-20496^c	215.07826	52.94850	6.786	${41.71}_{-0.23}^{+0.23}$	${1410}_{-200}^{+200}$	${6.45}_{-0.18}^{+0.18}$	D. D. Kocevski et al. (2024)
CEERS-20777^c	214.89225	52.87741	5.286	${42.13}_{-0.03}^{+0.03}$	${1690}_{-70}^{+70}$	${6.84}_{-0.04}^{+0.04}$	D. D. Kocevski et al. (2024)
PRIMER-UDS-29881^c	34.31313	−5.22677	6.170	${41.89}_{-0.12}^{+0.12}$	${2280}_{-220}^{+220}$	${6.98}_{-0.11}^{+0.11}$	D. D. Kocevski et al. (2024)
PRIMER-UDS-31092^c	34.26458	−5.23254	5.675	${42.20}_{-0.05}^{+0.05}$	${2160}_{-130}^{+130}$	${7.10}_{-0.06}^{+0.06}$	D. D. Kocevski et al. (2024)
PRIMER-UDS-32438^c	34.24181	−5.23940	3.500	${41.80}_{-0.04}^{+0.04}$	${2420}_{-120}^{+120}$	${6.98}_{-0.05}^{+0.05}$	D. D. Kocevski et al. (2024)
PRIMER-UDS-33823^c	34.24419	−5.24583	3.103	${43.76}_{-0.02}^{+0.02}$	${2700}_{-130}^{+130}$	${8.16}_{-0.04}^{+0.04}$	D. D. Kocevski et al. (2024)
PRIMER-UDS-116251^c	34.26054	−5.20912	5.365	${41.55}_{-0.21}^{+0.21}$	${1540}_{-280}^{+280}$	${6.44}_{-0.20}^{+0.20}$	D. D. Kocevski et al. (2024)
PRIMER-UDS-119639^c	34.31214	−5.20255	6.518	${42.15}_{-0.09}^{+0.09}$	${2200}_{-400}^{+400}$	${7.09}_{-0.17}^{+0.17}$	D. D. Kocevski et al. (2024)

Notes. D. D. Kocevski et al. (2024) did not provide the Hα luminosities of their objects. The Hα luminosities quoted here for objects for D. D. Kocevski et al. (2024) are computed using the SMBH masses and Hα line widths provided by D. D. Kocevski et al. (2024), according to their Equation (5).

^aThe SMBH masses are calculated using the Hα broad emission line. The errors in the table only contain statistical errors; the systematic errors of the black hole mass is about 0.3 dex.^bThe references from which the objects are gathered.^cObjects in the photometrically selected LRD sample in D. D. Kocevski et al. (2024; i.e., the color-selected sample defined in Section 2.1).

Download table as: ASCII Typeset image

Note that we did not apply any additional color cuts when putting together this sample of LRDs. In contrast, previous studies have employed various color cuts in constructing their LRD samples. In a recent study, D. D. Kocevski et al. (2024) provided a comprehensive discussion on LRD color selection and compiled a photometrically selected sample with homogeneous color cuts across multiple JWST surveys. Their sample selection, described in Section 3.1 of D. D. Kocevski et al. (2024), requires objects to have blue SED slopes in the rest-frame UV and red SED slopes in the rest-frame optical. We find that 18 of the LRDs from D. D. Kocevski et al. (2024) are included in our sample. These 18 objects form a sample of spectroscopically confirmed LRDs with homogeneous color properties and enable us to assess the impact of sample selection on our results. We refer to these objects as the “color-selected subset” throughout this study.

2.2. Stacking Analysis

We use CSTACK (T. Miyaji & R. E. Griffiths 2008)⁴ to analyze the archival Chandra observations. CSTACK is an online tool for stacking the archival ACIS-I observations in several Chandra deep fields. Our targets are covered by the CDF-N (2Ms), CDF-S (7Ms), AEGIS-XD, and X-UDS data sets in CSTACK. CSTACK takes the positions of objects as inputs and sums the photons within certain apertures at these positions. In this work, we use circular apertures that correspond to an enclosed counts fraction (ECF) of 0.9 and only include observations where the target has an off-axis angle (θ_off) smaller than 8′. The background levels of observations are estimated using the square regions centered on the source positions with sizes of 30″ × 30″, excluding the inner circular regions with a radius of 7″. The background level is then subtracted from the source flux. The output of CSTACK includes the stacked photon count rates and their errors in the soft (0.5–2 keV) and hard (2–8 keV) X-ray bands as well as the stacked images in the two bands.

To exclude objects not suitable for stacking analysis (e.g., those with bright companions) and to enable a flexible analysis of their physical properties, we run CSTACK first for individual LRDs instead of the whole sample. We visually inspect the images of individual objects and exclude five objects with bright companions or uneven background, which can cause inaccurate background estimation and subtraction. For the remaining objects, we obtain the photon counts in source and background regions in individual Chandra observations from CSTACK and use these quantities to derive the posterior probability of the count rate for each source and for the sample stack (Section 2.3).

Another factor to consider for stacking X-ray observations is the off-axis angle of objects. The point-spread function (PSF) of Chandra strongly depends on the off-axis angle; according to the Chandra Proposers Observatory Guide,⁵ the PSF of Chandra only changes subtly at ${\theta }_{{\rm{off}}}\lt 2{\rm{^{\prime} }}$ and quickly becomes fatter and more eccentric at larger radii. Fat and eccentric PSFs can introduce systematic errors in aperture correction and background subtraction. In CSTACK, this effect is accounted for by performing photometry using apertures corresponding to ECF = 0.9. By requiring ${\theta }_{{\rm{off}}}\lt 8{\rm{^{\prime} }}$ , more than 80% of the observations we analyzed have aperture radii smaller than 3″. To further investigate the impact of large off-axis angles, we construct another subset of LRD observations with object off-axis angle ${\theta }_{{\rm{off}}}\lt 2{\rm{^{\prime} }}$ , which is referred to as “2′ subset” in the rest of this Letter. We will compare the result for this subset and the whole sample in Section 3.

2.3. X-Ray Count Rate Limits

We then evaluate the upper limit of the photon rates for individual LRDs and for the whole sample. Since our targets only have a few (or zero) photons in their source apertures, we need to use Poisson statistics instead of Gaussian distributions to describe the photon rates. We note that CSTACK estimates the error of the stacked flux by bootstrapping the sample, which does not work for individual objects. To derive the posterior distribution of photon rates for individual objects, we follow the algorithm used by the aprates ⁶ task in CIAO (A. Fruscione et al. 2006). We briefly describe this algorithm below.

For the ith image to be stacked, CSTACK computes the photon rate of a source as follows:

$\begin{eqnarray}&&{r}_{s,i}=\left[\displaystyle \frac{{N}_{i}}{{t}_{i}}-\displaystyle \frac{{N}_{b,i}{A}_{s,i}}{{t}_{b,i}{A}_{b,i}}\right]/\mathrm{ECF},\end{eqnarray} \tag{ 1 }$

where N_i (N_b,i) is the number of photons within the source aperture (within the background region), t_i (t_b,i) is the exposure time on the source (on the background region), and A_s,i (A_b,i) is the area of the source aperture (background region). The stacked photon rate, r_s, can then be computed as

$\begin{eqnarray}&&{r}_{s}=\displaystyle \frac{{\sum }_{i}{t}_{i}{r}_{s,i}}{{\sum }_{i}{t}_{i}}=\displaystyle \frac{{\sum }_{i}{N}_{i}}{\mathrm{ECF}{\sum }_{i}{t}_{i}}-\displaystyle \frac{1}{\mathrm{ECF}{\sum }_{i}{t}_{i}}{\sum }_{i}\displaystyle \frac{{N}_{b,i}{t}_{i}{A}_{s,i}}{{t}_{b,i}{A}_{b,i}}.\end{eqnarray} \tag{ 2 }$

CSTACK delivers the observed values of N_i and N_b,i, which we denote as ${N}_{i}^{\mathrm{obs}}$ and ${N}_{b,i}^{\mathrm{obs}}$ . These photon counts follow the Poisson distribution. In the rest of this Letter, we use N_i and N_b,i to denote the expectation of the Poisson distributions. According to Bayes’s Theorem, the probability for the observation to have an expected photon count of N_i in the source aperture is

$\begin{eqnarray}&&P({N}_{i}| {N}_{i}^{\mathrm{obs}})=\displaystyle \frac{P({N}_{i}^{\mathrm{obs}}| {N}_{i})P({N}_{i})}{P({N}_{i}^{\mathrm{obs}})}=\displaystyle \frac{{N}_{i}^{{N}_{i}^{\mathrm{obs}}}{e}^{-{N}_{i}}}{{N}_{i}^{\mathrm{obs}}!}.\end{eqnarray} \tag{ 3 }$

For the second equal sign, we assume an uninformative flat prior for N_i and normalize the probabilistic distribution. Similarly, for N_b,i we have

$\begin{eqnarray}&&P({N}_{b,i}| {N}_{b,i}^{\mathrm{obs}})=\displaystyle \frac{{N}_{b,i}^{{N}_{b,i}^{\mathrm{obs}}}{e}^{-{N}_{b,i}}}{{N}_{b,i}^{\mathrm{obs}}!}.\end{eqnarray} \tag{ 4 }$

The probabilistic distribution of r_s can be determined by combining Equations (1), (2), (3), and (4). We also compute the full band (0.5–8 keV) by combining the soft and hard band count rate distributions.

Table 2 lists the evaluated count rates for individual objects and for the whole sample. None of the LRDs are detected individually in either the soft or hard band with more than 2.6σ significance. After stacking all objects in our sample, we get tentative detections in the soft and the hard bands with 2.9σ and 3.2σ significance. Combining the two bands gives a 4.1σ detection in the full band for the whole sample stack. This result indicates that AGN activity likely exists in the broad Hα emitters in our sample. The color-selected subset and the 2′ subset do not show significant detections (>3σ) in any band, possibly due to shorter stacked exposure time for the subsets.

Table 2. Photon Rates for Individual Objects and the Stacked Whole Sample

Name	Field	${N}_{{\rm{H}}}^{\mathrm{MW}}$ ^a	${t}_{\exp }$ ^b	$\overline{{\theta }_{\mathrm{off}}}$ ^c	Rate_soft	Rate_hard	Rate_full
		(10²⁰ cm⁻²)	(Ms)	(arcmin)	(10⁻⁶ cts s⁻¹)	(10⁻⁶ cts s⁻¹)	(10⁻⁶ cts s⁻¹)
CEERS-00397	AEGIS	0.94	0.69	4.1	${1.31}_{-3.37}^{+4.39}$	$-{2.07}_{-5.81}^{+6.81}$	$-{0.26}_{-6.96}^{+7.98}$
CEERS-00672	AEGIS	0.95	0.71	2.9	$-{1.40}_{-0.82}^{+1.77}$	${1.71}_{-4.17}^{+5.19}$	${0.75}_{-4.42}^{+5.44}$
CEERS-00717	AEGIS	0.95	0.67	2.4	$-{0.59}_{-0.87}^{+1.89}$	${1.92}_{-3.47}^{+4.56}$	${1.82}_{-3.80}^{+4.89}$
CEERS-00746	AEGIS	0.92	0.69	3.4	$-{0.55}_{-1.58}^{+2.60}$	${5.26}_{-5.22}^{+6.26}$	${5.21}_{-5.66}^{+6.69}$
CEERS-01236	AEGIS	0.94	0.70	3.8	${1.46}_{-2.53}^{+3.55}$	${1.81}_{-5.01}^{+6.03}$	${3.77}_{-5.86}^{+6.88}$
CEERS-01244	AEGIS	0.93	0.67	6.2	$-{6.61}_{-5.38}^{+6.27}$	${8.79}_{-12.32}^{+13.23}$	${2.61}_{-13.63}^{+14.53}$
CEERS-01665	AEGIS	0.93	0.70	4.7	${11.04}_{-5.30}^{+6.28}$	$-{9.80}_{-7.29}^{+8.12}$	${1.70}_{-9.24}^{+10.13}$
CEERS-02782	AEGIS	0.93	0.72	1.5	${1.79}_{-1.50}^{+2.49}$	$-{1.06}_{-2.05}^{+3.05}$	${1.21}_{-2.85}^{+3.86}$
GOODS-N-13733	CDF-N	0.96	1.64	4.2	${0.13}_{-2.49}^{+2.90}$	${4.87}_{-4.75}^{+5.16}$	${5.20}_{-5.45}^{+5.86}$
GOODS-N-16813	CDF-N	0.98	1.20	4.0	$-{1.77}_{-1.53}^{+2.10}$	${8.30}_{-4.80}^{+5.40}$	${6.80}_{-5.14}^{+5.74}$
GOODS-N-4014	CDF-N	0.98	1.59	3.5	${1.36}_{-1.72}^{+2.17}$	${0.47}_{-3.08}^{+3.52}$	${2.05}_{-3.63}^{+4.07}$
GOODS-S-13971	CDF-S	0.69	6.74	1.5	${0.35}_{-0.34}^{+0.44}$	$-{0.02}_{-0.85}^{+0.98}$	${0.38}_{-0.94}^{+1.06}$
M23-10013704-2	CDF-S	0.69	5.72	0.9	$-{0.04}_{-0.25}^{+0.38}$	$-{0.20}_{-0.83}^{+0.99}$	$-{0.18}_{-0.90}^{+1.05}$
M23-20621	CDF-N	0.98	1.48	4.0	$-{3.08}_{-1.29}^{+1.73}$	${3.41}_{-4.36}^{+4.83}$	${0.55}_{-4.63}^{+5.10}$
M23-3608	CDF-N	0.98	1.05	2.6	${2.63}_{-1.94}^{+2.62}$	${2.16}_{-3.33}^{+4.02}$	${5.13}_{-4.02}^{+4.71}$
M23-53757-2	CDF-N	0.97	1.48	3.4	${5.17}_{-2.33}^{+2.82}$	${8.81}_{-4.04}^{+4.52}$	${14.22}_{-4.77}^{+5.26}$
M23-73488-2	CDF-N	0.97	1.50	3.6	${1.62}_{-1.52}^{+2.00}$	${2.37}_{-2.97}^{+3.44}$	${4.23}_{-3.44}^{+3.92}$
M23-77652	CDF-N	0.97	1.68	3.5	${0.08}_{-1.52}^{+1.94}$	$-{0.67}_{-3.09}^{+3.50}$	$-{0.39}_{-3.53}^{+3.95}$
M23-8083	CDF-S	0.69	5.70	0.8	$-{0.07}_{-0.25}^{+0.38}$	$-{0.18}_{-0.84}^{+0.99}$	$-{0.19}_{-0.90}^{+1.05}$
CEERS-5760	AEGIS	0.94	0.68	4.6	${2.94}_{-3.62}^{+4.57}$	${8.36}_{-8.70}^{+9.53}$	${11.74}_{-9.62}^{+10.48}$
CEERS-6126	AEGIS	0.94	0.63	6.4	$-{8.78}_{-5.05}^{+5.90}$	${24.74}_{-13.85}^{+14.78}$	${16.37}_{-14.91}^{+15.83}$
CEERS-7902	AEGIS	0.94	0.58	3.6	${1.33}_{-2.53}^{+3.76}$	${4.80}_{-6.05}^{+7.29}$	${6.74}_{-6.83}^{+8.08}$
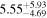
CEERS-10444	AEGIS	0.93	0.58	1.9	${3.72}_{-2.48}^{+3.71}$	${1.21}_{-3.56}^{+4.79}$	${5.55}_{-4.69}^{+5.93}$
CEERS-13135	AEGIS	0.95	0.63	5.9	$-{3.93}_{-4.60}^{+5.61}$	${8.15}_{-10.37}^{+11.41}$	${4.71}_{-11.56}^{+12.59}$
CEERS-13318	AEGIS	0.95	0.61	4.6	${5.33}_{-4.58}^{+5.69}$	$-{3.05}_{-8.45}^{+9.48}$	${2.81}_{-9.86}^{+10.91}$
CEERS-14949	AEGIS	0.94	0.66	2.8	$-{0.50}_{-0.88}^{+1.93}$	${6.45}_{-4.44}^{+5.55}$	${6.45}_{-4.72}^{+5.83}$
CEERS-20496	AEGIS	0.95	0.71	3.7	${0.34}_{-2.08}^{+3.06}$	${4.84}_{-5.63}^{+6.62}$	${5.66}_{-6.21}^{+7.20}$
CEERS-20777	AEGIS	0.94	0.59	4.5	${7.10}_{-5.00}^{+6.20}$	$-{5.75}_{-7.49}^{+8.63}$	${1.93}_{-9.30}^{+10.46}$
PRIMER-UDS-29881	X-UDS	2.01	0.33	5.1	$-{7.38}_{-5.18}^{+6.89}$	$-{0.01}_{-13.17}^{+14.95}$	$-{6.56}_{-14.56}^{+16.33}$
PRIMER-UDS-31092	X-UDS	1.98	0.29	3.9	${22.12}_{-11.57}^{+13.72}$	${7.16}_{-15.27}^{+16.78}$	${30.20}_{-19.69}^{+21.44}$
PRIMER-UDS-32438	X-UDS	1.98	0.23	3.7	${0.88}_{-4.82}^{+7.81}$	${4.41}_{-9.94}^{+12.86}$	${6.71}_{-11.85}^{+14.80}$
PRIMER-UDS-33823	X-UDS	1.98	0.26	3.7	${3.00}_{-5.69}^{+8.32}$	${5.82}_{-10.39}^{+12.91}$	${10.09}_{-12.54}^{+15.10}$
PRIMER-UDS-116251	X-UDS	2.04	0.32	4.6	${14.95}_{-8.22}^{+10.31}$	$-{1.64}_{-11.80}^{+13.33}$	${14.23}_{-14.89}^{+16.62}$
PRIMER-UDS-119639	X-UDS	2.01	0.42	5.5	${9.05}_{-7.72}^{+9.29}$	${5.58}_{-13.17}^{+14.48}$	${15.36}_{-15.61}^{+17.00}$

Whole Sample	⋯	⋯	42.86	2.7	${1.03}_{-0.37}^{+0.38}$	${2.37}_{-0.76}^{+0.78}$	${3.21}_{-0.80}^{+0.82}$
Color-selected subset	⋯	⋯	14.66	2.9	${1.48}_{-0.72}^{+0.77}$	${3.59}_{-1.54}^{+1.58}$	${4.79}_{-1.60}^{+1.64}$
2′ subset	⋯	⋯	22.30	1.1	${0.67}_{-0.23}^{+0.27}$	${0.37}_{-0.49}^{+0.52}$	${1.00}_{-0.54}^{+0.58}$

Notes. For count rates, the values are the 16th, 50th, and 84th percentiles of the distributions. The “soft,” “hard,” and “full” bands stand for 0.5–2 keV, 2–8 keV, and 0.5–8 keV, respectively.

^aThe column density of the Milky Way absorption.^bThe total effective exposure time reported by CSTACK.^cThe mean off-axis angle of the object, weighted by the exposure time of observations.

Download table as: ASCII Typeset image

In the rest of this Letter, we define upper limits as the values corresponding to a cumulative probability of 99.87%. This definition is equivalent to a 3σ upper limit in a Gaussian distribution.

2.4. Estimating Physical Fluxes and Luminosities

We convert photon rates (in counts per second) to fluxes (in ergs per second per square centimeter) of the LRDs using the Chandra Proposal Planning Toolkit.⁷ Note that the sensitivity of Chandra degrades with time. To account for this effect, CSTACK rescales the exposure maps of archival Chandra observations to match the sensitivity of certain Chandra cycles. Following the manual of CSTACK, we use the conversion factors of Cycle 10 for CDF-S, Cycle 3 for CDF-N, Cycle 9 for AEGIS, and Cycle 16 for X-UDS. We use a power law with photon index Γ = 1.8 to describe the unabsorbed X-ray spectra of LRDs. To evaluate the impact of AGN photoelectric absorption, we consider three different column densities, i.e., N_H = 10²¹, 10²², and 10²³ cm⁻². We note that N_H = 10²² cm⁻² is usually considered the boundary between type I and type II AGNs (e.g., M. Koss et al. 2017; C. Ricci et al. 2017; C. Panagiotou & R. Walter 2019). We use the online HEASoft tool⁸ to obtain the column densities of the Milky Way absorption, where we adopt the column density map from HI4PI Collaboration et al. (2016).

We also compute the upper limits of the unabsorbed X-ray luminosities at rest-frame 2–10 keV (L_X) for the LRDs. For each object, we compute the upper limit of L_X indicated from soft, hard, and total band fluxes, then choose the lowest value as the upper limit of L_X. We find that soft band fluxes give the tightest constraint in nearly all cases. The estimated physical fluxes and luminosity upper limits are listed in Table 3.

Table 3. Derived Fluxes and Luminosity Limits of the Sample

Name	N_H = 10²¹ cm⁻²				N_H = 10²² cm⁻²				N_H = 10²³ cm⁻²
	F_soft ^a	F_hard ^b	F_full ^c	L_X ^d	F_soft	F_hard	F_full	L_X	F_soft	F_hard	F_full	L_X
CEERS-00397	${0.74}_{-1.91}^{+2.49}$	$-{3.86}_{-10.84}^{+12.72}$	$-{0.49}_{-13.00}^{+14.89}$	<4.82	${0.73}_{-1.89}^{+2.47}$	$-{3.86}_{-10.84}^{+12.72}$	$-{0.49}_{-13.00}^{+14.89}$	<4.90	${0.69}_{-1.78}^{+2.32}$	$-{3.88}_{-10.89}^{+12.78}$	$-{0.49}_{-13.05}^{+14.95}$	<5.72
CEERS-00672	$-{0.79}_{-0.46}^{+1.00}$	${3.18}_{-7.78}^{+9.68}$	${1.41}_{-8.25}^{+10.16}$	<1.83	$-{0.79}_{-0.46}^{+0.99}$	${3.18}_{-7.78}^{+9.68}$	${1.41}_{-8.25}^{+10.16}$	<1.87	$-{0.74}_{-0.43}^{+0.94}$	${3.20}_{-7.81}^{+9.72}$	${1.41}_{-8.29}^{+10.20}$	<2.24
CEERS-00717	$-{0.33}_{-0.49}^{+1.07}$	${3.59}_{-6.48}^{+8.51}$	${3.40}_{-7.10}^{+9.13}$	<3.35	$-{0.33}_{-0.49}^{+1.06}$	${3.59}_{-6.48}^{+8.51}$	${3.40}_{-7.10}^{+9.13}$	<3.39	$-{0.31}_{-0.46}^{+1.00}$	${3.61}_{-6.51}^{+8.55}$	${3.42}_{-7.13}^{+9.17}$	<3.77
CEERS-00746	$-{0.31}_{-0.89}^{+1.47}$	${9.81}_{-9.75}^{+11.68}$	${9.72}_{-10.57}^{+12.50}$	<2.56	$-{0.31}_{-0.89}^{+1.46}$	${9.81}_{-9.75}^{+11.68}$	${9.72}_{-10.57}^{+12.50}$	<2.61	$-{0.29}_{-0.84}^{+1.37}$	${9.85}_{-9.79}^{+11.73}$	${9.76}_{-10.61}^{+12.55}$	<3.13
CEERS-01236	${0.83}_{-1.43}^{+2.01}$	${3.38}_{-9.35}^{+11.26}$	${7.04}_{-10.93}^{+12.85}$	<2.22	${0.82}_{-1.42}^{+2.00}$	${3.38}_{-9.35}^{+11.26}$	${7.04}_{-10.93}^{+12.85}$	<2.30	${0.77}_{-1.34}^{+1.88}$	${3.39}_{-9.39}^{+11.31}$	${7.07}_{-10.98}^{+12.90}$	<3.08
CEERS-01244	$-{3.74}_{-3.05}^{+3.55}$	${16.40}_{-23.00}^{+24.70}$	${4.87}_{-25.44}^{+27.13}$	<2.19	$-{3.71}_{-3.02}^{+3.52}$	${16.40}_{-23.00}^{+24.70}$	${4.87}_{-25.44}^{+27.13}$	<2.27	$-{3.50}_{-2.85}^{+3.32}$	${16.47}_{-23.10}^{+24.80}$	${4.89}_{-25.55}^{+27.25}$	<3.04
CEERS-01665	${6.25}_{-3.00}^{+3.55}$	$-{18.29}_{-13.61}^{+15.16}$	${3.18}_{-17.25}^{+18.91}$	<4.68	${6.21}_{-2.98}^{+3.53}$	$-{18.29}_{-13.61}^{+15.16}$	${3.18}_{-17.25}^{+18.91}$	<4.84	${5.84}_{-2.80}^{+3.32}$	$-{18.37}_{-13.67}^{+15.22}$	${3.19}_{-17.33}^{+18.99}$	<6.18
CEERS-02782	${1.01}_{-0.85}^{+1.41}$	$-{1.99}_{-3.82}^{+5.70}$	${2.26}_{-5.31}^{+7.20}$	<2.57	${1.01}_{-0.84}^{+1.40}$	$-{1.99}_{-3.82}^{+5.70}$	${2.26}_{-5.31}^{+7.20}$	<2.63	${0.95}_{-0.79}^{+1.32}$	$-{2.00}_{-3.84}^{+5.72}$	${2.27}_{-5.34}^{+7.23}$	<3.25
GOODS-N-13733	${0.06}_{-1.14}^{+1.33}$	${10.01}_{-9.77}^{+10.62}$	${10.69}_{-11.21}^{+12.06}$	<1.64	${0.06}_{-1.13}^{+1.32}$	${10.02}_{-9.78}^{+10.62}$	${10.69}_{-11.22}^{+12.06}$	<1.69	${0.06}_{-1.09}^{+1.27}$	${10.05}_{-9.82}^{+10.66}$	${10.73}_{-11.26}^{+12.11}$	<2.14
GOODS-N-16813	$-{0.81}_{-0.70}^{+0.96}$	${17.06}_{-9.87}^{+11.10}$	${13.99}_{-10.57}^{+11.80}$	<1.12	$-{0.81}_{-0.70}^{+0.96}$	${17.07}_{-9.88}^{+11.11}$	${13.99}_{-10.58}^{+11.81}$	<1.14	$-{0.78}_{-0.67}^{+0.92}$	${17.13}_{-9.91}^{+11.15}$	${14.05}_{-10.62}^{+11.85}$	<1.44
GOODS-N-4014	${0.62}_{-0.79}^{+0.99}$	${0.97}_{-6.33}^{+7.23}$	${4.22}_{-7.46}^{+8.37}$	<1.50	${0.62}_{-0.78}^{+0.99}$	${0.97}_{-6.33}^{+7.24}$	${4.22}_{-7.47}^{+8.38}$	<1.54	${0.60}_{-0.76}^{+0.95}$	${0.97}_{-6.36}^{+7.27}$	${4.24}_{-7.50}^{+8.41}$	<1.96
GOODS-S-13971	${0.21}_{-0.20}^{+0.26}$	$-{0.05}_{-1.65}^{+1.90}$	${0.75}_{-1.82}^{+2.06}$	<0.47	${0.21}_{-0.20}^{+0.26}$	$-{0.05}_{-1.65}^{+1.90}$	${0.75}_{-1.82}^{+2.06}$	<0.48	${0.20}_{-0.19}^{+0.24}$	$-{0.05}_{-1.66}^{+1.91}$	${0.75}_{-1.82}^{+2.07}$	<0.58
M23-10013704-2	$-{0.02}_{-0.15}^{+0.22}$	$-{0.38}_{-1.62}^{+1.92}$	$-{0.34}_{-1.73}^{+2.03}$	<0.41	$-{0.02}_{-0.15}^{+0.22}$	$-{0.39}_{-1.62}^{+1.92}$	$-{0.34}_{-1.74}^{+2.03}$	<0.42	$-{0.02}_{-0.14}^{+0.21}$	$-{0.39}_{-1.62}^{+1.92}$	$-{0.34}_{-1.74}^{+2.04}$	<0.50
M23-20621	$-{1.41}_{-0.59}^{+0.79}$	${7.02}_{-8.97}^{+9.94}$	${1.12}_{-9.51}^{+10.48}$	<0.48	$-{1.40}_{-0.59}^{+0.79}$	${7.02}_{-8.98}^{+9.95}$	${1.12}_{-9.52}^{+10.48}$	<0.49	$-{1.35}_{-0.57}^{+0.76}$	${7.05}_{-9.01}^{+9.98}$	${1.13}_{-9.55}^{+10.52}$	<0.66
M23-3608	${1.20}_{-0.89}^{+1.20}$	${4.44}_{-6.85}^{+8.26}$	${10.54}_{-8.27}^{+9.69}$	<2.09	${1.20}_{-0.88}^{+1.19}$	${4.44}_{-6.85}^{+8.27}$	${10.55}_{-8.28}^{+9.69}$	<2.15	${1.16}_{-0.85}^{+1.15}$	${4.46}_{-6.88}^{+8.30}$	${10.59}_{-8.31}^{+9.73}$	<2.72
M23-53757-2	${2.37}_{-1.06}^{+1.29}$	${18.12}_{-8.30}^{+9.30}$	${29.25}_{-9.81}^{+10.81}$	<1.71	${2.36}_{-1.06}^{+1.28}$	${18.13}_{-8.31}^{+9.30}$	${29.26}_{-9.81}^{+10.81}$	<1.77	${2.27}_{-1.02}^{+1.24}$	${18.20}_{-8.34}^{+9.34}$	${29.37}_{-9.85}^{+10.85}$	<2.45
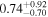
M23-73488-2	${0.74}_{-0.70}^{+0.92}$	${4.87}_{-6.10}^{+7.08}$	${8.70}_{-7.08}^{+8.06}$	<0.88	${0.74}_{-0.69}^{+0.91}$	${4.87}_{-6.11}^{+7.08}$	${8.70}_{-7.09}^{+8.07}$	<0.93	${0.71}_{-0.67}^{+0.88}$	${4.89}_{-6.13}^{+7.11}$	${8.74}_{-7.11}^{+8.10}$	<1.33
M23-77652	${0.03}_{-0.70}^{+0.89}$	$-{1.37}_{-6.34}^{+7.20}$	$-{0.79}_{-7.26}^{+8.12}$	<1.18	${0.03}_{-0.69}^{+0.88}$	$-{1.37}_{-6.35}^{+7.20}$	$-{0.79}_{-7.27}^{+8.12}$	<1.21	${0.03}_{-0.67}^{+0.85}$	$-{1.38}_{-6.37}^{+7.23}$	$-{0.80}_{-7.29}^{+8.15}$	<1.53
M23-8083	$-{0.04}_{-0.15}^{+0.22}$	$-{0.36}_{-1.62}^{+1.91}$	$-{0.37}_{-1.74}^{+2.03}$	<0.24	$-{0.04}_{-0.15}^{+0.22}$	$-{0.36}_{-1.62}^{+1.92}$	$-{0.37}_{-1.74}^{+2.03}$	<0.25	$-{0.04}_{-0.14}^{+0.21}$	$-{0.36}_{-1.63}^{+1.92}$	$-{0.38}_{-1.75}^{+2.04}$	<0.33

Notes. For fluxes, the values reflect the 16th, 50th, and 84th percentiles of the distributions. The upper limits of luminosities correspond to a cumulative probability of 0.9987, which is equivalent to 3σ limits of Gaussian distributions.

^aThe flux in 0.5–2 keV derived from Rate_soft in Table 2, in 10⁻¹⁷ erg s⁻¹ cm⁻².^bThe flux in 2–8 keV derived from Rate_hard in Table 2, in 10⁻¹⁷ erg s⁻¹ cm⁻².^cThe flux in 0.5−8 keV derived from Rate_full in Table 2, in 10⁻¹⁷ erg s⁻¹ cm⁻².^dThe upper limit of the X-ray luminosity in rest frame 2–10 keV, which is the minimum of the upper limits derived from Rate_soft, Rate_hard, and Rate_full in Table 2, in 10⁴³ erg s⁻¹.

Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.

Download table as: Machine-readable (MRT)Typeset image

All the data and code used in this work, including more detailed information about individual observations used in the stacking analysis and the posterior distribution of the photon count rates, are available at https://github.com/cosmicdawn-mit/xray_lrd.

3. Results

We now consider the implication of the stacking results. The tentative X-ray detections for the whole sample stack indicate that AGN activity is likely present in LRDs; however, it is still unclear whether these objects have properties similar to other broad-line AGNs.

One of the key arguments in support of the hypothesis that AGN are present in LRDs is the observation of broad Balmer, e.g., Hα, emission lines. However, type I AGN activity is not the only plausible source of broad Hα lines. Outflows driven by star formation (e.g., S. Arribas et al. 2014; R. L. Davies et al. 2019; N. M. Förster Schreiber & S. Wuyts 2020) and supernovae (e.g., V. F. Baldassare et al. 2016) can also produce broad Hα emission lines. To test whether the broad Hα lines are indeed linked to AGN activity, we consider the relation between the X-ray luminosity and the Hα luminosity that has been found in low-redshift AGNs (e.g., L. C. Ho et al. 2001; Y. Shi et al. 2010). Specifically, we adopt the relation measured by C. Jin et al. (2012a), i.e.,

$\begin{eqnarray}&&\mathrm{log}{L}_{{\rm{X}}}[\mathrm{erg}\ {{\rm{s}}}^{-1}]=0.83\times \mathrm{log}{L}_{{\rm{H}}\alpha }[\mathrm{erg}\ {{\rm{s}}}^{-1}]+8.35.\end{eqnarray} \tag{ 5 }$

The scatter of this relation is about 0.3 dex. Note that the Hα luminosity in this relation corresponds to the broad Hα component. C. Jin et al. (2012a) showed that narrow Hα lines in AGNs have weaker correlation with X-ray luminosities compared to broad Hα lines. Assuming that the X-ray emissions and the broad Hα lines of LRDs are produced in the same way as the emission in low-redshift type I AGNs, we expect that these objects should follow the observed L_X–L_Hα relation.⁹

Figure 1 shows the L_X–L_Hα relation for low-redshift AGNs and for the LRDs. Most LRDs lie below the L_X–L_Hα relation. In particular, several LRDs with L_Hα ≳ 10⁴³ erg s⁻¹ have X-ray upper limits that are ∼1–2 dex weaker than expected from the L_X−L_Hα relation. We notice that the three panels (corresponding to N_H = 10²¹, 10²², and 10²³ cm⁻²) show very little difference, indicating that the impact of column density in our analysis is negligible at N_H ≲ 10²³ cm⁻². These results indicate that, at least for LRDs with the strongest Hα emissions, the X-ray emission is exceptionally weak. A recent study by B. Wang et al. (2024) also found similar results, who investigated a luminous LRD at z = 3.1 and concluded that its X-ray emission must be about 100 times fainter than the expected value given its optical luminosity.

Figure 1. Refer to the following caption and surrounding text. — **Figure 1.** The L_X−L_Hα relation. The gray crosses represent low-redshift type I AGNs from C. Jin et al. (2012c). The dashed line marks the relation as given by Equation (5). The open circles are the upper limits derived using the soft band flux limits for individual LRDs. Most of the upper limits are below the L_X–L_Hα relation; in particular, the two LRDs with the largest Hα luminosities have X-ray upper limits ∼1–2 dex lower than the relation. Column density has very little impact on our results for N_H ≲ 10²³ cm⁻².
Download figure:
Standard image High-resolution image

Stacking the whole sample allows us to put a more stringent constraint on the X-ray fluxes of the entire LRD population. Since the LRDs have different redshifts, it is not clear how to convert the stacked photon rates to physical fluxes and rest-frame luminosities. Instead, we convert the Hα luminosities to the expected photon rates for individual LRDs and average these expected rates using the same weight when stacking (i.e., the exposure time; see Equation (2)) to evaluate the expected stacked photon rates.

In Figure 2, we present the results for N_H = 10²² cm⁻². We note that column densities have negligible impacts on the results at N_H ≲ 10²³ cm⁻², as demonstrated by Figure 1 and Table 3. In the soft band, the upper limit of the whole sample stack is ∼1 dex lower than the expected value derived from the Hα luminosity. The differences between the expected stacked rates and the observed upper limits are ∼0.3 and ∼0.8 dex in the hard and full bands for the whole sample. Stacking the color-selected subset and the 2′ subset leads to similar conclusions. These results indicate again that the X-ray emission of LRDs is significantly weaker than typical type I AGNs.

Figure 2. Refer to the following caption and surrounding text. — **Figure 2.** Comparing the observed upper limit of the observed count rates and the expected values from Hα luminosities. The dashed lines mark the x = y relation in the plots. The three columns from left to right reflect the soft, the hard, and the full band. The upper limit of the stacked rate in the soft band is ∼1 dex below the expected value; this difference is about 0.3 dex for the hard band and 0.8 dex for the full band. The conclusions are very similar for the color-selected subset and the 2′ subset, suggesting that the observed X-ray weakness is not a result of selection effects or large off-axis angle observations. This figure shows the case for N_H = 10²² cm⁻², and the results are very similar for N_H = 10²¹ cm⁻² and N_H = 10²³ cm⁻². Note that the whole sample stack has tentative detections (see Table 2), but we still plot the upper limits to be consistent with the subsets that only have nondetections.
Download figure:
Standard image High-resolution image

Lastly, we note that recent studies (T. T. Ananna et al. 2024; R. Maiolino et al. 2024) also performed X-ray stacking analysis for LRDs using different samples, which confirmed that LRDs have weak X-ray emission compared to their bolometric luminosities. The weak X-ray emissions of LRDs is also consistent with H. Padmanabhan & A. Loeb (2023), who found that the measured UV emissivity of LRDs would imply an X-ray background ∼10 times higher than constrained by previous observations, assuming LRDs have SEDs similar to typical type I AGNs.

4. Discussion

The tentative X-ray detections after stacking the whole sample indicate that LRDs likely exhibit AGN activity. However, Section 3 shows that the X-ray emissions from LRDs are weak, suggesting that there are some key differences between LRDs and low-redshift type I AGNs. It is unlikely that the weak X-ray emissions are a result of selection effects or large off-axis angle observations since the color-selected subset and the 2′ subset have X-ray upper limits much lower than the expected levels. In this section, we discuss possible explanations for the observed X-ray weakness of LRDs.

4.1. Strong X-Ray Absorption

We first consider the possibility that the faint X-ray emission is a result of absorption. Our analysis shows that the soft band upper limit is about 1 dex lower than the expected value even when assuming N_H = 10²³ cm⁻². To move the stacked soft band upper limit to the mean L_X–L_Hα relation, we need to adopt a column density of 10^24.2 cm⁻², putting these AGNs into the Compton thick regime. We also note that column densities have little impact on the stacked hard band rate, which is ∼0.3 dex lower than the L_X–L_Hα relation.

Most type I AGNs have N_H ∼ 10²⁰–10²³ cm⁻² (e.g., M. Koss et al. 2017; C. Panagiotou & R. Walter 2019; T. T. Ananna et al. 2022b). Since the LRDs in our sample exhibit broad Hα lines, it is highly unlikely that these objects have such high column densities of ≳10²⁴ cm⁻². Some broad absorption line (BAL) quasars have high column densities (N_H ≳ 10²⁴ cm⁻²; e.g., A. J. Blustin et al. 2008; J. A. Rogerson et al. 2011) though LRDs with rest-frame UV spectra do not show strong BAL features (e.g., J. E. Greene et al. 2024; R. Maiolino et al. 2023).¹⁰ We also notice that some low-redshift type I AGNs have N_H > 10²⁴ cm⁻² (e.g., T. T. Ananna et al. 2022a); however, these AGNs are very rare, which only occupy a small fraction (≲5%) of the entire type I AGN population. In comparison, LRDs are numerous, the number density of which is ∼1 dex higher than the quasar luminosity function and is only ∼2 dex lower than the galaxy luminosity function at similar redshifts (J. E. Greene et al. 2024; D. D. Kocevski et al. 2024). We thus consider it unlikely that absorption is the only reason for the low X-ray fluxes of LRDs.

4.2. Intrinsically Faint X-Ray Emission

Alternatively, we suggest that LRDs might be a population of AGNs with intrinsically faint X-ray emission, implying a low L_X/L_Hα ratio. Specifically, the inner accretion disk and the corona of LRDs might be different from other type I AGNs. It is also possible that LRDs have unique broad-line region properties, such that their Hα line fluxes are higher than other type I AGNs.

Previous studies have pointed out that the ratio between optical and X-ray fluxes for AGNs (i.e., α_OX) increases with Eddington ratio (e.g., R. V. Vasudevan & A. C. Fabian 2007; C. Jin et al. 2012b). The Eddington ratios of LRDs have been estimated to be λ_Edd ∼ 0.05–2 (e.g., Y. Harikane et al. 2023; R. Maiolino et al. 2023), which is comparable to the AGN sample used to derive the L_X−L_Hα relation in C. Jin et al. (2012a). However, we note that the intrinsic Eddington ratio of LRDs might be higher than the reported values due to dust attenuation (e.g., J. Matthee et al. 2024). Therefore, high Eddington ratios might contribute to the low observed L_X/L_Hα ratios of LRDs. Recent theoretical models have shown that super-Eddington accretion could indeed be a possible solution to explain the X-ray weakness of LRDs (e.g., F. Pacucci & R. Narayan 2024; M. Volonteri et al. 2024). Since the estimated Eddington ratios of LRDs, however, still have large uncertainties, we leave a more quantitative investigation to future studies.

We note that the intrinsic L_X/L_Hα ratios of LRDs might be even lower than indicated in Figure 1. Most current modes of LRDs suggest large dust attenuations (A_V ≳ 2; e.g., D. D. Kocevski et al. 2024; P. G. Pérez-González et al. 2024). Furthermore, some models have suggested that the broad emission lines of LRDs are produced by scattered light from the central type I AGN, which is only a small fraction of the intrinsic emissions (e.g., J. E. Greene et al. 2024). Consequently, the intrinsic Hα luminosities of LRDs might be larger than the observed values, leading to lower intrinsic L_X/L_Hα ratios.

4.3. Broad Balmer Emission Lines due to Outflows

Another scenario previously proposed is that AGN activity only has partial contribution to the observed broad Hα lines of LRDs. Some other mechanisms can also produce Hα emission lines with FWHM ≳ 1000 km s⁻¹, including strong outflows driven by star formation or supernovae (e.g., V. F. Baldassare et al. 2016; R. L. Davies et al. 2019; N. M. Förster Schreiber & S. Wuyts 2020). This hypothesis agrees with the result from recent MIRI observations (P. G. Pérez-González et al. 2024), who found that starburst galaxies might have a major contribution to the near-to-mid-infrared SED of LRDs. However, recent NIRSpec observations have shown that LRDs have narrow [O iii] emission lines (e.g., R. Maiolino et al. 2024), which are hard to explain by the outflow scenario. Therefore, we consider it unlikely that outflows have major contributions to the broad Hα emission lines in LRDs.

Future JWST/NIRSpec observations will characterize the fluxes, kinematics, and spatial extents of the UV and optical emission lines for larger LRD samples, which will provide more clues about the contribution of outflows to the broad Hα lines.

In any case, our results indicate that we need to be cautious when applying previous knowledge about type I AGNs to these LRDs. In particular, the bolometric luminosities and the SMBH masses of LRDs estimated from the scaling relations for type I AGNs might have significant systematic uncertainties.

5. Conclusions

We investigate the X-ray properties of 34 LRDs using a stacking analysis. The LRD sample is compiled from the literature and is selected to show broad Hα emission lines with FWHM > 1000 km s⁻¹, indicating possible type I AGN activity. None of the individual LRDs are detected in soft or hard bands. After stacking the whole sample, the soft, hard, and full bands exhibit tentative detections with 2.9σ, 3.2σ, and 4.1σ significance, respectively. These tentative detections indicate that AGN activity likely presents in LRDs.

We further compared the X-ray flux upper limits of LRDs to their Hα luminosities. The upper limit on the soft (hard) band flux is ∼1 dex (∼0.3 dex) lower than the expected level from the L_X–L_Hα relation of low-redshift type I AGN, suggesting that LRDs are weak in X-ray emissions. This conclusion holds for the subset with uniform color cuts and the subset with small off-axis angle observations.

Our result suggests that LRDs might be a population of AGNs with distinct properties compared to previously identified type I AGNs, i.e., LRDs might have intrinsically weak X-ray emissions. We find it difficult to explain the observed weak X-ray fluxes of LRDs solely by absorption, and it is also unlikely that fast outflows have a major contribution to the broad Hα lines. In any case, caution should be taken when applying the empirical relations derived from other type I AGNs to the LRD population.

The sample of LRDs is rapidly increasing thanks to the ongoing imaging and spectroscopic surveys with JWST. With a larger LRD sample in the near future, we expect that a stacking analysis will put even stronger constraints on the X-ray properties of LRDs. Furthermore, upcoming JWST/NIRSpec observations will greatly increase the sample of spectroscopically confirmed LRDs and will reveal the fluxes, kinematics, and spatial extents of the other optical and UV emission lines of these objects. Future X-ray missions, such as the Advanced X-Ray Imaging Satellite (C. S. Reynolds et al. 2023), will offer much deeper images than Chandra and will likely solve the puzzles about the X-ray properties of LRDs.

Acknowledgments

We thank the anonymous referee for valuable comments. We thank Thomas Connor for valuable comments. T.T.A. acknowledges support from ADAP grant 80NSSC23K0557. T.M. and the development of the CSTACK tool are supported by the UNAM-DGAPA PAPIIT IN114423. The scientific results reported in this Letter are based on observations made by the Chandra X-ray Observatory. This work made use of software provided by the Chandra X-ray Center (CXC) in the CIAO application package.

Facility: CXO - Chandra X-ray Observatory satellite.

Software: CSTACK, CIAO, sherpa (P. Freeman et al. 2001; D. Burke & O. Laurino 2020), xspec (K. A. Arnaud 1996).