Speeding up polynomial GCD, a crucial operation in Maple

Abstract

Given two multivariate polynomials A and B with integer coefficients
we present a new GCD algorithm which computes G = gcd(A,B).
Our algorithm is based on the Hu/Monagan GCD algorithm.
If A = G A̅ and B = G B̅  we have modified the Hu/Monagan
so that it can interpolate the smaller of G and A̅.

We have implemented the new GCD algorithm in Maple with
several subroutines coded in C for efficiency.
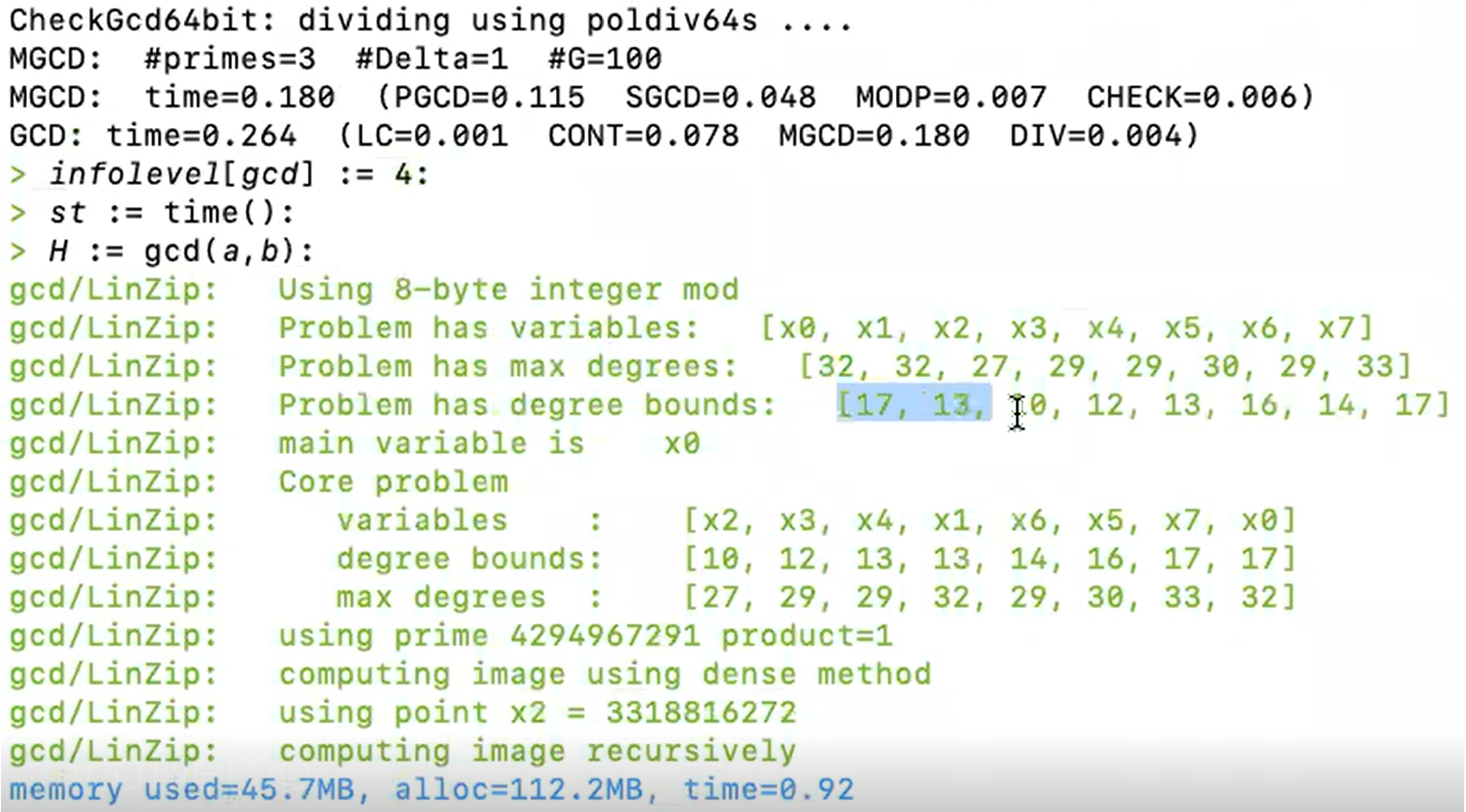
Maple currently uses Zippel's sparse modular GCD algorithm.
We present timing results comparing Maple's implementation of Zippel's algorithm