Les algorithmes d’approximation

Les algorithmes d’approximationElaboré Par: Ismail Wael Cours pour 3SI

IntroductionEn générale les fonctions mathématiques donne un résultat exacte.Exemple:f(x)=2x-2Pour f(x)=0 x=1Dans certains cas la valeur de x est impossible (ou presque) à déterminer.Exemple:f(x)=x3+x2+1Ci-dessous la courbe de la fonction f(x).X=1 donc la valeur de x pour la quelle f(x) s’annule est connue et est déterminé 2

Introductionf(x)= x3+x2+1xValeur de x pourLa quelle f(x)=0La valeur est illisible sur le repère,Elle est aussi indéterminée Mathématiquement.La solution est de dégager une valeurApprochée de x ou approximative.3

Les problèmes d’optimisation Le plus court chemin:Une personne veut se déplacer du point A vers la point B sachant que le déplacement à la nage se fait à la vitesse de 3 m/s tandis que la marche se fait à la vitesse de 5 m/s.Quel chemin cette personne doit elle parcourir pour pouvoir arriver en un minimum de temps?36mBrivière12mA4

Considérons le problème comme suit:De A à D est la distance nagé et de D à B est le chemin parcouru au sol, il reste à savoir la distance CD donc (x)Calculer la distance AD en fonction de x:AD2=AC2+X2AD=D= Ds+De avec Dsdistance au sol et De  distance dans l’eau36mDCxB12mA5

Les problèmes d’optimisation 36mDCxB12mADe= AD=Ds=36-xD= +36-x V=D/TT=D/VT=6

Les problèmes d’optimisationf(x)f(x) optimale7

Algorithme de la fonction valeur_opt0)fonction valeur_opt(pas:réel):réel1)t02)x53)xmin04)tmin5)Répeter t xx+pas si (tmin>t)alorstmintxminxfinsiJusqu’à (x>10)6)valeur_optxmin7)Fin valeur_opt8

ApplicationUne compagnie loue, à des groupes de 15 personnes ou plus, des bus d'excursion dont la capacité est de 80 personnes. Si un groupe compte exactement 15 personnes, chacune d'elles doit payer 90 dinars. Pour les groupes plus nombreux, le tarif par personne est réduit de n dinars lorsque n personnes s'ajoutent aux premières.On se propose de déterminer l'effectif d'un groupe pour que la location d'un bus rapporte un revenu maximal.En déduire le réel x0 de l'intervalle [0..65] en le quel la fonction f atteint son maximum local.9

Réponsele bus contient au maximum 80 personnesChaque personne supérieur au groupe de 15 entraine une réduction de 1 D par personne.Si le groupe est constitué de 20 personne:Montant_loc=20*85=1700 D20=15+5 85=90-5L’inconnu est le nombre de personne à rajouter au groupe (x) pour avoir un montant de location maximal:En fonction de x la formule devient:Monatant_max=(15+x)*(90-x)10

Montant de la location(f(x))Nombre de personne (x)11

Les algorithmes d’approximationACB Diviser l’espace en surfaces Calculables.La surface totale hachurée (ST) est la somme des surfaces A,B et C.ST=A+B+COn sait que ST=25 alors25=A+B+C A+B+C-25=012

Les algorithmes d’approximationA=((2.5)2 *3,14)/2=9.812B=25-5xC=((5-2x)/2)2 *3,14)/2 =9.812-1.57x2 A+B+C-25=09.812+25-5x+ 9.812-1.57x2 -25=0 -1.57x2 -5x+19.624=013

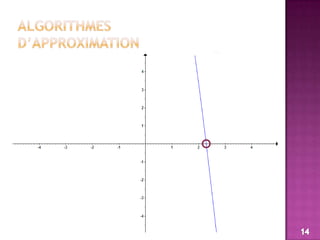
Algorithmes d’approximation14

algorithmes d’approximationOn veut écrire un programme qui permet de chercher et d'afficher le zéro de cette fonction (f(x) = 0) avec une précision epsilon donnée.On utilise la méthode de recherche par dichotomie:• On divise l'intervalle [a, b] par 2• Soit m le milieu de cet intervalle. Si f(m) et f(a) sont de même signe, le zéro recherché estdans [m, b], sinon il est dans [a, m].• Répéter les étapes précédentes jusqu'à (b-a) devient inférieure ou égale à epsilon, dans ce cas, la valeur de m correspond à la valeur approchée de la solution de l'équation f(x)=0.15

principef(x) = -1.57x2 -5x+19.624, avec x ∈[0,5/2]On a f(0) = 19.624, f(5/2) = -2.6885 d’où : f(a).f(b) = f(0).f(5/2) <0Donc on peut appliquer la méthode dichotomique sur [0,5/2]Pour ce la :• Diviser [0,2.5] par 2 m = (0+2.5)/2 = 1.25• f(1.25) = 11.412• f(m).f(0) = 11.412* 19,624 >0 (sont de même signe)Le zéro est dans [m, b]= [1.25, 2.5]…16

ANALYSERésultat = Afficher le zéro de fDonnées = a, b, epsTraitement =Saisie (a,b,eps)Écrire ("Le zéro de f est = ", zéro (a, b, eps))Analyse de la fonction zéroRésultat = mTraitement =Zéro mm  (a+b)/2Tant Que (b-a) >eps et f(m) <>0 FaireSi f(a)*f(m)>0 Alorsa  mSinon b  mFin Sim(a+b)/2Fin Tant Que17

Algorithme de la fonction zéro0) Fonction zéro (a, b, eps : réel) : réel1) m  (a+b)/22) Tant Que (b-a) >eps et f(m) <>0 FaireSi f(a)*f(m)>0 Alorsa  mSinon b m, Fin Sim(a+b)/2Fin Tant Que3) Zérom4) Fin zéro18

Algorithme de la fonction f0) Fonction f (x : réel) : réel1) f  -1.57x2 -5x+19.6242) Fin fEn pascal19

Les algorithmes d’approximation

Contenu connexe

Tendances (20)

Similaire à Les algorithmes d’approximation (20)

Plus de Wael Ismail (20)

Les algorithmes d’approximation