Acute Angled Triangle

Acute angled triangle is a triangle in which all the angles of the triangles are acute angles. A triangle can have only one angle as either a right angle or an obtuse angle because of the angle sum property of the triangle. And hence, the triangle having all three angles as acute angles i.e. angles having a value less than 90 degrees is called an acute-angled triangle.

Based on the types of interior angles of the triangle, a triangle can be classified into three categories, Acute-Angled Triangles, Obtuse-Angled Triangles, and Right-Angled Triangles. Now let's learn more about acute-angled triangles, their types, properties, and others in detail in this article.

What is an Acute-Angled Triangle?

An acute-angled triangle is defined as a triangle whose all three interior angles are acute, i.e., their value is between 0° and 90°. Based on the type of triangle, the side lengths of an acute-angled triangle can be equal or unequal. An acute-angled triangle also follows the angle sum property of the triangle.

The figure given below is an acute-angled triangle whose interior angles are 45°, 35°, and 80°. Since the three interior angles are less than 90°, the given triangle is an acute-angled triangle.

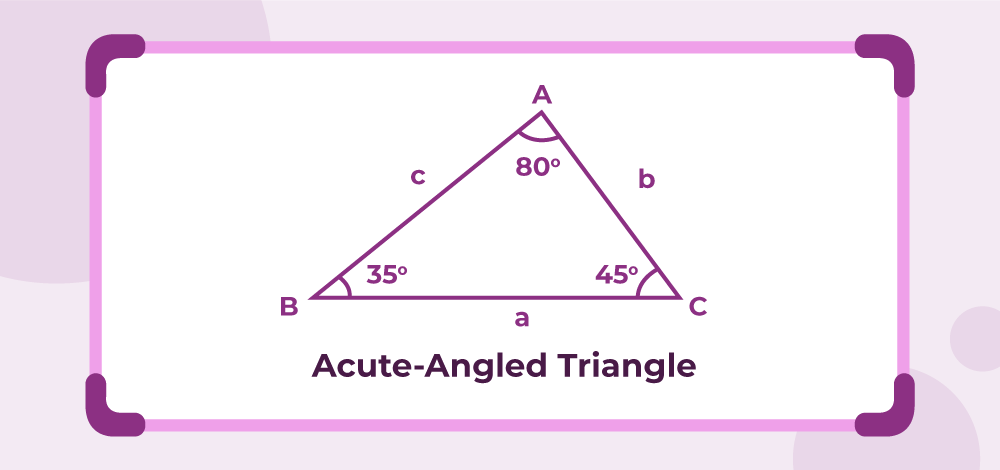
Acute-Angled Triangle Definition

Acute-angled triangles are defined as the name suggests as triangles in which all three angles of the triangle are acute angles. The side in acute-angled triangles can be equal or unequal and based on that they are further divided into three parts that are discussed in the article below,

Types of Acute-Angled Triangles

Acute-angled triangles are classified into three types depending on the side lengths of the triangles, 

• Equilateral Acute Triangle
• Isosceles Acute Triangle
• Scalene Acute Triangle

Now let's learn more about them in detail.

Equilateral Acute Triangle

An equilateral acute triangle also called an equilateral triangle is a triangle in which all the angles are acute angles and all the angles are equal also the side of the equilateral acute triangles are also equal. Each angle of an equilateral acute triangle always measures 60°.

Isosceles Acute Triangle

An isosceles acute triangle is a triangle in which all the angles are acute angles and any two angles of the triangle and the side corresponding to these angles are equal. That is in the isosceles acute triangle we have two sides and their corresponding angles equal.

Scalene Acute Triangle

A scalene acute triangle is a triangle in which all the angles are acute angles and no two angles and no two sides are equal. That is in the scalene acute triangle we have no sides and no angles equal.

Properties of Acute-Angled Triangle

The following are some important properties of an acute-angled triangle,

• Interior angles of the acute-angled triangle are acute angles i.e. the angles are greater than 0° but less than 90°.
• Interior angles of the acute-angled triangles follow the angle sum property, i.e. the sum of the angles of the acute-angled triangle is 180°.
• An equilateral triangle is always an acute-angled triangle since each interior angle of an equilateral triangle measures 60°.
• A triangle cannot simultaneously be a right-angled triangle and an acute-angled triangle.
• A triangle cannot simultaneously be an acute-angled triangle and an obtuse-angled triangle.
• In the acute angle triangle, the side opposite the smallest angle is the smallest and its converse is also true.
• Similarly, the side opposite the largest angle is the largest and its converse is also true.

Acute-Angled Triangle Formulas

The area and perimeter are the two basic formulas of an acute-angled triangle which are discussed below.

Perimeter of Acute-Angled Triangle

The perimeter of an acute-angled triangle is equal to the sum of its three side lengths. If a, b, and c are the side lengths of an acute-angled triangle, then its perimeter is given as (a + b + c) units.

Perimeter of Acute-Angled Triangle = (a + b + c) units

Where a, b, and c are the side lengths of the triangle.

Read More, Perimeter of a Triangle

Area of Acute-Angled Triangle

The area of a triangle is defined as the total space enclosed by the three sides of any triangle in a two-dimensional plane.

Area of Acute-Angled Triangle = ½ × b × h

Where,

• "b" is the base length, and
• "h" is the height of the triangle.

Read More, Area of a Triangle

Acute Triangle Area by Heron's Formula

If the three side lengths of an acute-angled triangle are given, then its area can be calculated using Heron's formula.

Area of Acute-Angled Triangle = \sqrt{s(s-a)(s-b)(s-c)} 

Where,

• "s" is the semi-perimeter and s = (a + b + c)/2, and
• a, b, and c are the side lengths of the triangle.

Read More, Heron’s Formula

Important Terminologies of Triangle

The various terminologies related to the acute-angled triangle are,

Circumcenter

The centre of the circle that passes the three vertices of the triangle is called the circumcenter of the triangle. It is calculated by taking the intersection point of the perpendicular bisector. For an acute-angled triangle, the circumcenter always lies inside the triangle.

Incenter

The centre of the circle that touches the three sides of the triangle is called the incenter of the triangle. It is calculated by taking the intersection point of the angular bisector. For an acute-angled triangle, the incenter always lies inside the triangle.

Centroid

The intersection of the medians of a triangle is called the centroid of the triangle. For an acute-angled triangle, the centroid of the triangle always lies inside the triangle.

Orthocenter

The intersection point of the altitude of the triangle is called the orthocentre of the triangle. For an acute-angled triangle, the orthocentre of the triangle always lies inside the triangle.

Solved Examples on Acute Angled Triangle

Example 1: Which of the following angles can form an Acute-Angled Triangle?

• a) 65°, 75°, 50°
• b) 95°, 40°, 45°
• c) 70°, 40°, 70°
• d) 90°, 45°, 45°

Solution:

We know that all the angles in the acute-angled triangle are acute angles that is their measure is less than, 90 degrees.

They also follow the angle sum property of a triangle, i.e. all their angles sum up to 180 degrees.

a) 65°, 75°, 50°

Here, all the angles are acute angles but it does not follow the angle sum property hence the triangle is not possible.

65°+ 75°+ 50° = 190° (Triangle not possible)

b) 95°, 40°, 45°

Here the triangle is possible, as it follows the angle sum propety of triangle, i.e.

95°+ 40°+ 45° = 180

But while observing the angles of the triangle we found an obtuse angle 95°. Hence the triangle is not an acute angle triangle.

c) 70°,40°,70°

Here the triangle is possible, as it follows the angle sum propety of triangle, i.e.

70°+ 40°+ 70° = 180

And while observing the angles of the triangle we found that all the angles are acute angles. Hence the triangle is an acute angle triangle.

d) 90°, 45°, 45°

Here the triangle is possible, as it follows the angle sum propety of triangle, i.e.

90°+ 45°+ 45° = 180

But while observing the angles of the triangle we found a right angle 90°. Hence the triangle is not an acute angle triangle.

Example 2: Find the perimeter of an acute triangle XYZ whose sides are XY = 8 units, YZ = 5 units, and XZ = 9 units.

Solution:

Given,

Sides of Acute- Angled Triangle,

• XY(x) = 8 units
• YZ(y) = 5 units
• XZ(z) = 9 units

We know that,

Perimeter of Acute-Angled Triangle (P) = x + y + z

⇒ P = (8 + 5 + 9) units

⇒ P = 22 units

Hence, the perimeter of the acute-angled triangle is 22 units.

Example 3: Find the area of an acute triangle whose height is 12 units and base is 15 units.

Solution:

Given,

• Height of triangle (h) = 12 units
• Length of base of triangle (b) = 15 units

We know that,

Area of the triangle (A) = ½ × b × h

⇒ A = ½ × 12 × 15 

⇒ A = ½ × 180 

⇒ A = 90 square units.

Hence, the area of the given acute triangle is 90 square units.

Example 4: Find the area of an acute triangle whose sides are AB = 5 cm, BC = 7 cm, and AC = 8 cm.

Solution:

Given,

Sides of Acute- Angled Triangle,

• AB = c = 5 units
• BC = a = 7 units
• AC = b = 8 units

We know that,

Area of Triangle =  \sqrt{s(s-a)(s-b)(s-c)} 

⇒ A = \sqrt{10(10-7)(10-8)(10-5)} 

⇒ A = \sqrt{10(3)(2)(5)} 

⇒ A = √(300) sq. cm

⇒ A = 10√3 sq. cm

Hence, the area of the given acute triangle is 10√3 sq. cm.