Adjacent Angles are the angles that have a common vertex, a common arm, and the rest two arms lie on either side of the common arm. Angles are particularly important in geometry as they help define and understand different geometric figures and their characteristics. Geometry is a branch of mathematics that focuses on shapes, sizes, and angles. A key concept within geometry is adjacent angles. Understanding adjacent angles helps us grasp the geometry of lines, polygons, and other shapes.
In this particular article, we are going to learn about adjacent angles, their definitions, their properties, and some examples and we will also practice some questions on it.

What is an Adjacent angle?
Adjacent angles are a pair of angles that share a common vertex and a common side but do not overlap. In simpler terms, they are angles that are side by side, touching at a single point, and not overlapping or intersecting.
The shared side is typically a ray, and the shared vertex is the endpoint of that ray. When two angles are adjacent and they form a straight line, also known as a straight angle.
Adjacent Angle Definition
The angles having a common vertex and a common side are known as adjacent angles. They are directly next to each other and do not overlap.
Examples of Adjacent Angles
Some of the Examples of Adjacent angles are mentioned below:
- Let's consider a door with hinges placed at its edge. The angles formed by the door and the frame at each hinge are called adjacent angles. These adjacent angles have a shared vertex (the hinge) and a shared side (the edge of the door).
- When you open a book and lay it flat, the pages form a straight line. The angles formed by the pages on the left and right sides of the crease are called adjacent angles. These angles share the crease as a common side and vertex.
- When two roads intersect, the angles formed where they meet are called adjacent angles. Each road serves as a shared side for two adjacent angles.
Properties of Adjacent Angle
The properties of Adjacent Angle in geometry are mentioned below:
- Common Vertex - The most critical property of adjacent angles is that they share a common vertex. The common endpoint is the point of intersection where the two rays meet.
- Common Side - Adjacent angles also share a common side. This means that one side of each angle is the same, and they form a straight line together.
- No Overlapping - Adjacent angles do not overlap; they are always next to each other. They have no interior points in common.
How to Identify Adjacent Angles?
We can identify adjacent angles, by using following steps [in no specific order]:
- Look for angles that share a common vertex and a common side.
- Check if the angles are formed by intersecting lines or rays.
- Ensure that the angles do not overlap.
- Confirm that the angles are next to each other, without any gaps between them.
Adjacent Angles in Parallelogram
In a parallelogram, two pairs of opposite angles are formed. Adjacent angles are those angles that share a common vertex and a common side, but they are not opposite angles.
Specifically, in a parallelogram:
- Opposite angles are congruent (they have the same measure).
- Adjacent angles are supplementary (the sum of their measures is 180°).
For example, in the diagram below, angles A and B are adjacent angles, as are angles C and D. Angle A and angle C are opposite angles, as are angle B and angle D.

So, if you know the measure of one angle in a parallelogram, you can find the measure of its adjacent angle by subtracting it from 180°.
Supplementary Adjacent Angles
Supplementary adjacent angles are pairs of adjacent angles whose measures add up to 180°. In other words, when two angles are supplementary, they form a straight line. However, in case of quadrilaterals such as parallelogramThis property is commonly observed in various geometric figures, including parallelograms, straight lines, and sometimes in triangles.
If you have a straight line, the angles on either side of the line are supplementary adjacent angles. For example, if angle A and angle B are adjacent angles on a straight line, then A + B = 180°.

In a parallelogram, opposite angles are congruent (have the same measure), and adjacent angles are supplementary. If angle A and angle B are adjacent angles in a parallelogram, then A + B = 180°.

Linear Pair Adjacent Angles
When adjacent angles form a straight line together, they are known as a linear pair. A linear pair of angles always adds up to 180°.

Complementary and Adjacent Angles
Complementary angles and adjacent angles are two different concepts in geometry.
Complementary angles are two angles that add up to 90°. In other words, if you have two angles, angle A and angle B, and they are complementary, then A + B = 90°. Complementary angles can be part of the same or different geometric figures; they don't have to share a common side or vertex.
Adjacent angles are two angles that share a common vertex and a common side. They are next to each other and have a common side but don't necessarily have to add up to any specific angle measure like complementary angles. Adjacent angles can be part of various geometric shapes, such as lines, polygons, or other figures.

However two angles can be complementary and adjacent as well. For Example if two adjacent angles sum up to 90° then we call that adjacent angles to be complementary as well.
Non-Adjacent Angles
Non-adjacent angles are angles that are not next to each other and do not share a common side or vertex. They are also referred to as "non-adjacent supplementary angles" when their measures add up to 180°. Non-adjacent angles can be found in various geometric shapes and configurations.
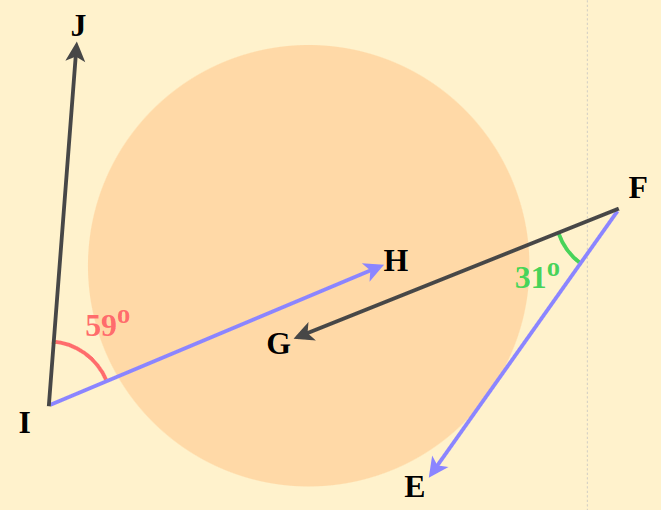
For Example, in a parallelogram, the angles that are opposite to each other are called Non-Adjacent Angles. Here, in the given parallelogram, A and C are Non-Adjacent Angles. Similarly, B and D are non-adjacent angles. In the figure attached below, angle I and angle F are also Non Adjacent Angles.
Conclusion
In conclusion, understanding adjacent angles is key in geometry. Recognizing angles that share a corner and a side helps solve geometric puzzles. Mastering this idea helps in both math and real life. So, keep spotting adjacent angles for better geometry skills and problem-solving!
Also, Check
Solved Examples on Adjacent Angle
Example 1: Find the measures of two complementary adjacent angles if one angle measures 45°.
Solution:
If two angles are complementary, their measures add up to 90°. In this case, we know one angle measures 45°. To find the other angle, we subtract 45 from 90:
90° - 45° = 45°
So, the other angle also measures 45°. Therefore, the two complementary adjacent angles are both 45°.
Example 2: In a right triangle, one of the acute angles measures 30°. Find the measure of the other acute angle.
Solution:
In a right triangle, one of the acute angles is always 90°. The other two angles are the acute angles. If one acute angle measures 30°, we can find the measure of the other acute angle by subtracting 30 from 90:
90° - 30° = 60°
The other acute angle measures 60°.
Example 3: In a right triangle, one of the acute angles measures 40°. Find the measure of the other acute angle.
Solution:
In a right triangle, one of the acute angles is always 90°, and the sum of the measures of the acute angles is 90°. So, to find the measure of the other acute angle when one angle is 40°, subtract 40° from 90°:
Other acute angle = 90° - 40° = 50°
The measure of the other acute angle is 50°.
Example 4: If two vertical angles are formed by intersecting lines, and one of them measures 75°, what is the measure of the other vertical angle?
Solution:
Vertical angles are always congruent, which implies they measure the same. Given that one vertical angle measures 75°, the other vertical angle will also measure 75°.
Example 5: Two adjacent angles are complementary. If one angle measures 35°, find the measure of the other angle.
Solution:
If two angles are complementary, their measures add up to 90°. Given that one angle measures 35°, we can find the other angle by subtracting 35° from 90°:
Other angle = 90° - 35° = 55°
So, the other angle measures 55°, and the two adjacent angles are 35° and 55°.
Practice Questions on Adjacent Angles
Q1. In a straight line, if one angle measures 40°, what is the measure of the adjacent angle?
Q2. In a parallelogram, if one of the adjacent angles measures 60°, what is the measure of the other adjacent angle?
Q3. In a triangle, if one of the adjacent angles measures 45°, what is the measure of the adjacent angle?
Q4. Two angles are adjacent, and their measures are in the ratio of 3:4. If the larger angle measures 120°, find the measure of the smaller angle.
Q5. In a quadrilateral, the measures of two adjacent angles are 65° and 115°. Find the measures of the other two adjacent angles.
Similar Reads
Examples of Adjacent Angles in Real Life Adjacent angles are one of the many types of angles defined in geometry. They can be observed frequently in our day-to-day lives, from the opening of doors to the arrangement of book pages to the folding of paper. In this article, we explore the presence of adjacent angles in real-life scenarios.Wha
4 min read
What is a common angle? Geometry is one of the most historic parts of Mathematics. It's an indispensable part of Ancient Mathematics. Geometry relates to the study of figures/line/points including different dimensions of figures/line/point such as measurement, position, size, surfaces, and shape. The different dimensions o
4 min read
GRE Geometry | Lines and Angles Lines: A Line is a one-dimensional geometrical figure having negligible breadth extending infinitely in both directions. A line may be straight or curved. A straight line has same direction throughout its whole length from point to point. A curved line changes it's direction continuously from point
4 min read
Lines in Geometry- Definition, Types and Examples A line in geometry is a straight path that goes on forever in both directions. It has no thickness and is usually drawn between two points, but it keeps going without stopping. Lines are important for making shapes, measuring distances, and understanding angles. For example, the edge of a ruler can
9 min read
What is an Acute Angle? An acute angle is an angle that measures less than 90 degrees but more than 0 degrees. These angles are smaller than a right angle and are often found in triangles and various geometric shapes. Imagine the angle formed when you bend your elbow, creating a sharp but not wide opening; this is an examp
9 min read
What is a Zero degree angle? An angle that does not form a vertex or measure 0 degrees is called a zero angle. It is also called zero radians. A zero angle is formed when both the rays or arms of the angle are pointing toward the same direction and the vertex as just a point without any space.When we observe an angle it consist
5 min read