The Binary Number System, also known as the base-2 system, uses only two digits, '0' and '1', to represent numbers. It forms the fundamental basis for how computers process and store data. This base-2 system is the backbone of how computers process and store information, representing everything from text to images as sequences of 0s and 1s.
The binary number (11001)₂ corresponds to the decimal number 25.
The word binary is derived from the word "bi," which is Latin for "two". But what makes it so essential, and how does it work? This article will dive deep into binary numbers, binary decimal number conversion and vice versa, 1's and 2's complements, and how they are used in computer systems.
Binary Number Table
Given below is the decimal number and the binary equivalent of that number.
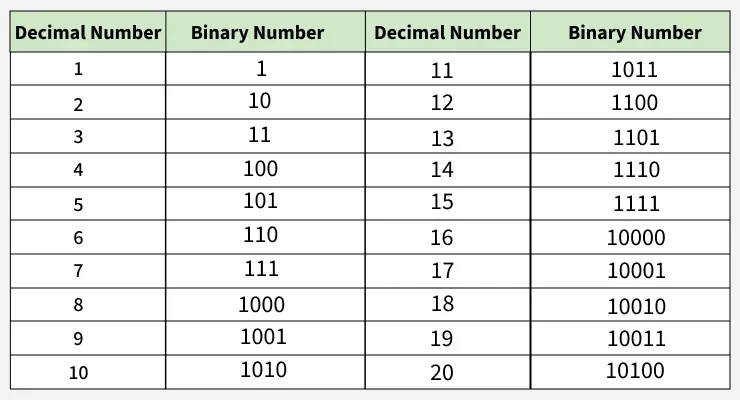Binary-Decimal Conversion TableConversion from Binary to Other Number Systems
Binary numbers use digits 0 and 1 and have a base of 2. Converting a binary number to another number system involves changing its base. The following outlines the conversion of binary numbers to other number systems:
Binary to Decimal Conversion
A binary number is converted into a decimal number by multiplying each digit of the binary numbers 1 or 0 to the corresponding to the power of 2 according to the place value.
Let us consider that a binary number has n digits, B = an-1...a3a2a1a0. Now, the corresponding decimal number is given as:
D = (an-1 × 2n-1) +...+(a3 × 23) + (a2 × 22) + (a1 × 21) + (a0 × 20)
Let us go through an example to understand the concept better.
Example: To convert (11101011)2 into a decimal number.
Steps:
- Step 1: Multiply each digit of the Binary number with the place value of that digit, starting from right to left i.e. from LSB to MSB.
- Step 2: Add the result of this multiplication and the decimal number will be formed.
Binary to Octal Conversion
Binary numbers have a base of 2, while octal numbers have a base of 8. To convert a binary number to an octal number, the base is changed from 2 to 8.
Example: To convert (11101011)2 into an octal number.
Steps:
- Step 1: Divide the binary number into groups of three digits starting from right to left i.e. from LSB to MSB.
- Step 2: Convert these groups into equivalent octal digits.
Binary to Hexadecimal Conversion
Binary numbers have a base of 2, while hexadecimal numbers have a base of 16. To convert a binary number to a hexadecimal number, group the digits appropriately and convert to the corresponding hexadecimal value.
Example: To convert (1110101101101)2 into a hex number.
Steps:
- Step 1: Divide the binary number into groups of four digits starting from right to left i.e. from LSB to MSB.
- Step 2: Convert these groups into equivalent hex digits.
Arithmetic Operations on Binary Numbers
We can easily perform various operations on Binary Numbers. Various arithmetic operations on the Binary number include,
Now, let's learn about the same in detail.
Binary Addition
The result of the addition of two binary numbers is also a binary number. To obtain the result of the addition of two binary numbers, we have to add the digits of the binary numbers digit by digit. The table below shows the rules of binary addition.
Binary Number (1) | Binary Number (2) | Addition | Carry |
|---|
0 | 0 | 0 | 0 |
0 | 1 | 1 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 1 |
Example: Find (1101)2 + (1011)2 = ?
\begin{array}{cccccc} & & 1 & 1 & 0 & 1 \quad (\text{13 in decimal}) \\+ & & 1 & 0 & 1 & 1 \quad (\text{11 in decimal}) \\\hline & 1 & 1 & 0 & 0 & 0 \quad (\text{24 in decimal})\end{array}
Binary Subtraction
The result of the subtraction of two binary numbers is also a binary number. To obtain the result of the subtraction of two binary numbers, we have to subtract the digits of the binary numbers digit by digit. The table below shows the rule of binary subtraction.
Binary Number (1) | Binary Number (2) | Subtraction | Borrow |
|---|
0 | 0 | 0 | 0 |
0 | 1 | 1 | 1 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 0 |
Example: Find (1011)2 - (1110)2 = ?
\begin{array}{cccccc} & 1 & 1 & 1 & 0 \quad (\text{14 in decimal}) \\- & 1 & 0 & 1 & 1 \quad (\text{11 in decimal}) \\\hline & 0 & 0 & 1 & 1 \quad (\text{3 in decimal})\end{array}
Binary Multiplication
The multiplication process of binary numbers is similar to the multiplication of decimal numbers. The rules for multiplying any two binary numbers are given in the table.
Binary Number (1) | Binary Number (2) | Multiplication |
|---|
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Example: Find (101)2 ⨉ (11)2 = ?
Solution:
\begin{array}{cccccc} & & 1 & 0 & 1 \\ \times & & & 1 & 1 \\\hline & & 1 & 0 & 1 \\+ & 1 & 0 & 1 & \times \\\hline & 1 & 1 & 1 & 1 \end{array}
Binary Division
The division method for binary numbers is similar to that of the decimal number division method. Let us go through an example to understand the concept better.
Example: Find (11011)2 ÷ (11)2 = ?
1's and 2's Complement of a Binary Number
- 1's Complement of a Binary Number is obtained by inverting the digits of the binary number.
Example: Find the 1's complement of (10011)2.
Solution:
Given Binary Number is (10011)2
Now, to find its 1's complement, we have to invert the digits of the given number.
To find the 1's complement of a binary number, you simply flip all the bits:
Thus, 1's complement of (10011)2 is (01100)2
- 2's Complement of a Binary Number is obtained by inverting the digits of the binary number and then adding 1 to the least significant bit.
Example: Find the 2's complement of (1011)2.
Solution:
Given Binary Number is (1011)2
To find the 2's complement, first find its 1's complement, i.e., (0100)2
Now, by adding 1 to the least significant bit, we get (0101)2
Hence, the 2's complement of (1011)2 is (0101)2
Uses of the Binary Number System
Binary Number Systems are used for various purposes, and the most important use of the binary number system is,
- Binary Number System is used in all Digital Electronics for performing various operations.
- Programming Languages use the Binary Number System for encoding and decoding data.
- Binary Number System is used in Data Sciences for various purposes, etc.
Solved Example of the Binary Number System
Example 1: Convert the Decimal Number (98)10 into Binary.
Solution:
Thus, Binary Number for (98)10 is equal to (1100010)2
Example 2: Convert the Binary Number (1010101)2 to a decimal Number.
Solution:
Given Binary Number, (1010101)2
= (1 × 20) + (0 × 21) + (1 × 22) + (0 × 23) + (1 × 24) + (0 × 25) + (1 ×26)
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85)10
Thus, Binary Number (1010101)2 is equal to (85)10 in decimal system.
Example 3: Divide (11110)2 by (101)2.
Solution:
Example 4: Add (11011)2 and (10100)2.
Solution:
Hence, (11011)2 + (10100)2 = (101111)2
Example 5: Subtract (11010)2 and (10110)2.
Solution:
Hence, (11010)2 - (10110)2 = (00100)2
Example 6: Multiply (1110)2 and (1001)2.
Solution:
Thus, (1110)2 × (1001)2 = (1111110)2
Example 7: Convert (28)10 into a binary number.
Solution:
Hence, (28)10 is expressed as (11100)2.
Example 8: Convert (10011)2 to a decimal number.
Solution:
The given binary number is (10011)2.
(10011)2 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (1 × 20)
= 16 + 0 + 0 + 2 + 1 = (19)10
Hence, the binary number (10011)2 is expressed as (19)10.
Practice Problem Based on Binary Number
Question 1. Convert the decimal number (98)₁₀ into binary.
Question 2. Divide the binary number (11110)₂ by (101)₂
Question 3. Find the 2's complement of the binary number (1011)₂.
Question 4. Multiply the binary numbers (1110)₂ and (1001)₂.
Question 5. Subtract the binary numbers (11010)₂ and (10110)₂.
Question 6. Add the binary numbers (11011)₂ and (10100)₂.
Answer:-
1. (1100010)2, 2. (110)2, 3. (0101)2, 4. (1111110)2, 5. (00100)2, 6. (101111)2
Suggested Quiz
4 Questions
What is the decimal equivalent of the binary number 101101?
Explanation:
101101 = (1×25) + (0×24) + (1×23) + (1×22) + (0×21) + (1×20) = 32 + 0 + 8 + 4 + 0 + 1 = 45.
Which of the following is a correct binary addition?
Explanation:
1011
+ 1101
11000
- 1 + 1 = 0 carry 1
- 1 + 0 + 1 = 0 carry 1
- 0 + 1 + 1 = 0 carry 1
- 1 + 1 + 1 = 1 carry 1
- Carry over: 1
Thus, the sum is 11000.
For other options:
B)
1010
+ 1000
10010
C)
1001
+ 0011
1100
D) This is same as first option.
Thus, only option A is correct.
What is the result of binary multiplication 101 × 11?
Explanation:
101
× 11
101 (As 101 × 1)
+ 1010 (As 101 × 10)
10011
Thus, the product is 10011.
Simplify (1011 ⋅ 100) + (101 ⋅ 110).
Explanation:
For 1011 ⋅ 100
1011
× 110
0000 (this is 1011×0)
+ 00000 (this is 1011×0, shifted one position left)
+ 101100 (this is 1011×1, shifted two positions left)
101100
For 101 ⋅ 110
101
× 110
000 (this is 101×0)
+ 1010 (this is 101×1, shifted one position left)
+ 10100 (this is 101×1, shifted two positions left)
11110
Now, 101100 + 11110 = 1001010
Quiz Completed Successfully
Your Score : 2/4
Accuracy : 0%
Login to View Explanation
1/4
1/4
< Previous
Next >
Similar Reads
Number System in Maths Number System is a method of representing numbers with the help of a set of symbols and rules; it is a mathematical notation used to represent quantities or values in various forms. The number system allows us to perform arithmetic operations and represent numbers consistently and understandably.A n
6 min read
What is a Number System? A number system is a way of writing numbers using specific symbols or digits. It helps us represent numbers mathematically. There are different types of number systems, such as the decimal system, binary system, octal system, and hexadecimal system.Here, we will discuss the types of number systems i
4 min read
Octal Number System The octal number system is a base-8 system using digits (0–7): 0, 1, 2, 3, 4, 5, 6, and 7. For example: 228, 138, 178, etc, are octal numbers. It is widely used in computer programming as a compact representation of binary numbers, where each octal digit corresponds to three binary digits.In this ar
6 min read
Number System Conversion in C Number system conversion is a fundamental concept in computer science and programming. It involves changing the representation of a number from one base to another, such as converting a decimal number to binary or a hexadecimal number to binary.In this article, we will create a console program in th
8 min read
Number System and Base Conversions Electronic and digital systems use various number systems such as Decimal, Binary, Hexadecimal and Octal, which are essential in computing. Binary (base-2) is the foundation of digital systems.Hexadecimal (base-16) and Octal (base-8) are commonly used to simplify the representation of binary data. T
9 min read
Binary Subtraction Binary Subtraction is a mathematical operation and is one of the four fundamental operations of binary numbers. Binary subtraction is similar to decimal subtraction but the rules used as somewhat different.Binary subtraction is a fundamental idea in binary operations. There are two components in bin
8 min read