Triangular Matrix | Types, Properties and Examples

Matrix is defined as a rectangular array of numbers that are arranged in rows and columns. The size of a matrix can be determined by the number of rows and columns in it. An "m by n" matrix has "m" rows and "n" columns and is written as an "m × n" matrix. For example, a matrix of order "5 × 6" has five rows and six columns. We have different types of matrices, such as rectangular, square, triangular, symmetric, singular, etc.

What is a Triangular Matrix?

Triangular matrix is a special case of a square matrix, where all elements above or below the principal diagonal are zeros. An upper triangular matrix is a square matrix, whose all elements below the principal diagonal are zeros. A lower triangular matrix is a square matrix, whose all elements above the principal diagonal are zeros. The matrices in the image given below are upper triangular and lower triangular matrices of order "4 × 4."

Types of Triangular Matrices

There are different types of matrices which are discussed below in this article:

• Upper Triangular Matrix: An upper triangular matrix is a square matrix, whose all elements below the principal diagonal are zeros.

U = \left[\begin{array}{ccc} a & b & c\\ 0 & d & e\\ 0 & 0 & f \end{array}\right]

• Lower Triangular Matrix:  A lower triangular matrix is a square matrix, whose all elements above the principal diagonal are zeros.

L = \left[\begin{array}{ccc} 1 & 0 & 0\\ 2 & 3 & 0\\ 4 & 5 & 6 \end{array}\right]

• Strictly Triangular Matrix: A triangular matrix is referred to as a strictly triangular matrix if all the elements of the principal diagonal are zero.
• Strictly Lower Triangular Matrix: A lower triangular matrix is referred to as a strictly lower triangular matrix if all the elements of the principal diagonal are zero.

A = \left[\begin{array}{ccc} 0 & 0 & 0\\ p & 0 & 0\\ q & r & 0 \end{array}\right]

• Strictly Upper Triangular Matrix: An upper triangular matrix is referred to as a strictly upper triangular matrix if all the elements of the principal diagonal are zero.

B = \left[\begin{array}{ccc} 0 & 12 & -7\\ 0 & 0 & 9\\ 0 & 0 & 0 \end{array}\right]

• Unit Triangular Matrix: A triangular matrix is referred to as a unit triangular matrix if all the elements of the principal diagonal are one.
• Unit Lower Triangular Matrix: A lower triangular matrix is referred to as a unit lower triangular matrix if all the elements of the principal diagonal are one.

P = \left[\begin{array}{ccc} 1 & 0 & 0\\ 2 & 1 & 0\\ 5 & 6 & 1 \end{array}\right]

• Unit Upper Triangular Matrix: An upper triangular matrix is referred to as a unit upper triangular matrix if all the elements of the principal diagonal are one.

Q = \left[\begin{array}{ccc} 1 & 21 & 19\\ 0 & 1 & 17\\ 0 & 0 & 1 \end{array}\right]

Upper Triangular Matrix

An upper triangular matrix is a square matrix, whose all elements below the principal diagonal are zeros. A square matrix "A = [a_ij]" is said to be an upper triangular matrix when a_ij = 0 for all i > j.

If U_n,n is a square matrix of order "n × n" and u_ij represents an element in the i^th row and j^th column of the given matrix, then

U_{n,n} = \left\{ \begin{array}{c} u_{ij},fori\leq j\\ 0,fori>j \end{array}\right\} 

Examples of Upper Triangular Matrix

The matrix given below is an upper triangular matrix of order "2 × 2." We can see that the elements below the principal diagonal are zeros.

U_{2,2} = \left[\begin{array}{cc} 13 & 9\\ 0 & 7 \end{array}\right]

The matrix given below is an upper triangular matrix of order "3 × 3."

U_{3,3} = \left[\begin{array}{ccc} 3 & -8 & 6\\ 0 & 5 & 11\\ 0 & 0 & 4 \end{array}\right]

Lower Triangular Matrix

A lower triangular matrix is a square matrix whose all elements above the principal diagonal are zeros. A square matrix "A = [a_ij]" is said to be a lower triangular matrix when a_ij = 0 for all i < j.

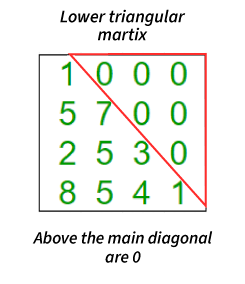
If L is a square matrix of order "n × n" and l_ij represents an element in the i^th row and j^th column of the given matrix, then the condition for the given matrix to be a lower triangular matrix is given as follows:

If L is a square matrix of order "n × n" and lij represents an element in the ith row and jth column of the given matrix, then the condition for the given matrix to be a lower triangular matrix is given as follows:

 L = \left\{ \begin{array}{c} l_{ij},fori\geq j\\ 0,fori<j \end{array}\right\} 

Examples of Lower Triangular Matrix

The matrix given below is a lower triangular matrix of order "2 × 2."

L = \left[\begin{array}{cc} 1 & 0\\ 3 & 5 \end{array}\right]

The matrix given below is a lower triangular matrix of order "3 × 3." We can see that the elements above the principal diagonal are zeros.

L_{3,3} = \left[\begin{array}{ccc} 4 & 0 & 0\\ 7 & 9 & 0\\ -5 & 3 & 11 \end{array}\right]

Properties of a Triangular Matrix

Various properties of the Triangular Matrix are discussed below in this article:

• The transpose of an upper triangular matrix is a lower triangular matrix, i.e., U^T = L, and the transpose of a lower triangular matrix is an upper triangular matrix, i.e., L^T = U.
• The determinant of a triangular matrix of any order is equal to the product of the principal diagonal elements.
• The inverse of a triangular matrix will also be a triangular matrix.
• A triangular matrix is invertible if and only if all elements of the principal diagonal are non-zero.
• When two triangular matrices are multiplied, the resultant matrix is also triangular.
• When two upper (lower) triangular matrices are multiplied, the resultant matrix is also an upper (lower) triangular matrix.
• When two upper (lower) triangular matrices are added, the resultant matrix is also an upper (lower) triangular matrix.

Also, Check

• Minors and Cofactors of Determinants
• Determinant of the Square Matrix
• Adjoint of the Square Matrix

Solved Examples on Triangular Matrix

Example 1: Calculate the determinant of the matrix given below.

A = \left[\begin{array}{ccc} 1 & 3 & -4\\ 0 & 7 & 0\\ 0 & 0 & 8 \end{array}\right]

Solution:

We can notice that the given matrix is an upper triangular matrix.

We know that the determinant of an upper triangular matrix of any order is equal to the product of the principal diagonal elements.

So, |A| = 1 × 7 × 8 = 56

Hence, the determinant of the given matrix is 56.

Example 2: Prove the inverse of the inverse of a lower triangular matrix will also be a lower triangular matrix.

Solution:

Let us consider a lower triangular matrix of order "2 × 2," to prove the inverse of the inverse of a lower triangular matrix will also be a lower triangular matrix.

L = \left[\begin{array}{cc} 5 & 0\\ -7 & 8 \end{array}\right]

L^-1 = Adj L/ |L|

|L| = 5 × 8 
    = 40

Adj L = \left[\begin{array}{cc} 8 & 0\\ 7 & 5 \end{array}\right]

L^{-1} = \frac{1}{40} \left[\begin{array}{cc} 8 & 0\\ 7 & 5 \end{array}\right]

We can see the inverse matrix is also a lower triangular matrix.

Hence, proved.

Example 3: Prove that the transpose of an upper triangular matrix is a lower triangular matrix.

Solution:

To prove that the transpose of an upper triangular matrix is a lower triangular matrix, let us consider an upper triangular matrix.

U = \left[\begin{array}{ccc} a & b & c\\ 0 & d & e\\ 0 & 0 & f \end{array}\right]

Now, U^{T} = \left[\begin{array}{ccc} a & 0 & 0\\ b & d & 0\\ c & e & f \end{array}\right]

We can notice that the resultant matrix is a lower triangular matrix.

Hence proved.

Example 4: Find the values of "a" and "b" in the given matrix P, if P is a unit lower triangular matrix.

P = \left[\begin{array}{cc} 2a+5 & 0\\ 5 & 3b-2 \end{array}\right]

Solution:

We know that a lower triangular matrix is referred to as a unit lower triangular matrix if all the elements of the principal diagonal are one.

So, 2a + 5 = 1 

2a = 1 − 5 = −4

a = −4/2 = −2

3b − 2 = 1

3b = 1 + 2 = 3

b = 3/3 
   = 1

Hence, the values of "a" and "b" are −2 and 1 respectively.

Conclusion

Triangular matrices are a specialized class of square matrices where all elements either above or below the principal diagonal are zeros, depending on whether the matrix is upper triangular matrix or lower triangular matrix. These matrices exhibit several important properties, such as their transposes converting between upper and lower triangular forms, the determinant being the product of the diagonal elements, and their inverse maintaining the triangular form if all diagonal elements are non-zero. Moreover, operations like multiplication and addition between triangular matrices result in matrices that retain the triangular structure.