A matrix is a rectangular array of numbers arranged in rows and columns. Each element in the matrix is identified by its position, which is denoted as "aij"​, where "i" is the row number and "j" is the column number of the element.
A matrix is typically represented as [A]m×n​, where m is the number of rows and n is the number of columns. Thus, the element of the matrix at the i-th row and j-th column can be represented as aij​.
In linear algebra, matrices can be classified into various types based on their properties, such as the values of their elements, as well as their order (dimensions).
Below is a visual representation of the different types of matrices, which will be explored in greater detail in this article.
The different types of matrices are mentioned below, let's learn about the types of matrices in detail.
Singleton Matrix
A matrix that has only one element is called a singleton matrix. In this type of matrix number of columns and the number of rows is equal to 1. A singleton matrix is represented as [a]1⨯1.
Example of a Singleton Matrix
Singleton MatrixIn the above example of the Singleton Matrix, there is only one element, 5. Hence, there is only one column and only one row.
Null Matrix
A matrix whose all elements are zero is called a Null Matrix. A null matrix is also called a Zero Matrix because all its elements are zero. An example of a null matrix is mentioned below:
Example of a Zero Matrix
Null matrixIn the above example of a null or zero matrix, all the elements are zero. Hence, the given example is a matrix of order 3 ⨯ 3 whose all elements are zero.
Row Matrix
A matrix that contains only one row and any number of columns is known as a row matrix. A row matrix is represented as [a]1⨯n, where 1 is the number of rows and n is the number of columns present in a row matrix. An example of a row matrix is given below.
Example of Row Matrix
Row matrixIn the above example of a row matrix, the number of rows is 1, and the number of columns is 3. Hence, the order of the matrix is 1 ⨯ 3.
Column Matrix
A matrix that contains only one column and any number of rows is called a Column Matrix. A Column Matrix is represented as [a]n⨯1 where n is the number of rows and 1 is the number of columns. An example of a column matrix is given below:
Example of Column Matrix
Column MatrixIn the above example of a column matrix, the number of rows is 4 and the number of columns is 1, thus making it a matrix of order 4 ⨯ 1.
Horizontal Matrix
A matrix in which the number of rows is lower than the number of columns is called a Horizontal Matrix.
Example of Horizontal Matrix
Horizontal MatrixIn the above matrix, the number of rows is 2 while the number of columns is 4, thus making it a horizontal matrix.
Vertical Matrix
The matrix in which the number of rows exceeds the number of columns is called a Vertical Matrix. A Vertical matrix is represented as [a]i⨯j where i > j. An example of a Vertical Matrix is mentioned below:
Example of Vertical Matrix
Vertical MatrixIn the above matrix, the number of rows is 4 while the number of columns is 2 thus making it a Vertical matrix.
Rectangular Matrix
A matrix that does not have an equal number of rows and columns is known as a Rectangular Matrix. A rectangular matrix can be represented as [A]m×n where m ≠n. An example of a rectangular matrix is mentioned below:
Example of Rectangular Matrix
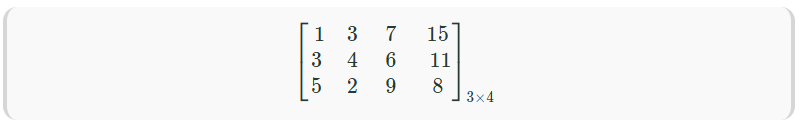Rectangular MatrixIn the above example, we see that the number of rows is 3 while the number of columns is 4, i.e. both are unequal, thus making it a rectangular matrix. We can say that both horizontal and vertical matrices are examples of rectangular matrices.
Square Matrix
A matrix that has an equal number of rows and an equal number of columns is called a Square Matrix. Generally, the representation used for the square matrix is [A]n×n. An example of a Square Matrix is mentioned below:
Example of aSquare Matrix
Square MatrixIn the above example of a Square Matrix, both the number of rows and columns are 3, thus making them seem like a square structure.
Diagonal Matrix
A matrix that has all elements as 0 except diagonal elements is known as a diagonal matrix. A Diagonal Matrix is only possible in the case of a Square Matrix. An example of a Diagonal Matrix is mentioned below:
Example of Diagonal Matrix
Diagonal MatrixIn the above example, the diagonal elements are 8, 4, and 9 and the rest elements are zero.
Scalar Matrix
A diagonal matrix whose all diagonal elements are non-zero and the same is called a Scalar Matrix. Scalar Matrix is a kind of diagonal matrix where all diagonal elements are the same. Identity Matrix is a special case of Scalar Matrix.
Example of Scalar Matrix
Scalar MatrixIn the above example, the given matrix is a diagonal matrix whose all diagonal elements are 4, and hence, this is an example of a Scalar Matrix.
Identity Matrix
A diagonal matrix where all the diagonal elements are 1 and all non-diagonal elements are 0 is called an Identity Matrix. The Identity Matrix is called the Unit Matrix. The identity matrix or unit matrix always has an equal number of rows and columns.
Example of Identity Matrix
Identity MatrixIn the above diagonal matrix of order 3 ⨯ 3, all the diagonal elements are 1, and non-diagonal elements are zero. Hence this diagonal matrix is an Identity Matrix.
Triangular Matrix
A square matrix in which the non-zero elements form a triangular below and above the diagonal is called a Triangular Matrix. Based on the triangle formed below or above the diagonal, the triangular matrix is classified as:
- Upper Triangular Matrix
- Lower Triangular Matrix
Upper Triangular Matrix
A square matrix in which all the elements below the diagonal are zero and the elements from the diagonal and above are non-zero elements is called an Upper Triangular Matrix. In an Upper Triangular Matrix, the non-zero elements form a triangular-like shape.
Example of Upper Triangular Matrix
Triangular Matrix
In the above example of the Upper Triangular Matrix, all the elements below the diagonal are zero.
Lower Triangular Matrix
A square matrix in which all the elements above the diagonal are zero and the elements from the diagonal and below are non-zero elements is called a Lower Triangular Matrix. In a Lower Triangular Matrix, the non-zero elements form a triangular-like shape from the diagonal and below.
Example of Lower Triangular Matrix
Triangular MatrixIn the above example of the lower triangular matrix, all the elements above the diagonal are zero.
Singular Matrix
A singular matrix is referred to as a square matrix whose determinant is zero and is not invertible.
If det A = 0, a square matrix "A" is said to be singular; otherwise, it is said to be non-singular.
Example of Singular Matrix
Singular Matrix
⇒ |A| = 3(12 × 6 - 18 × 4) - 6(6 × 6 - 18 × 2) + 9(6 × 4 - 12 × 2)
⇒ |A| = 3(72 - 72) - 6(36 - 36) + 9(24 - 24)
⇒ |A| = 3 × 0 - 6 × 0 + 9 × 0 = 0
Non Singular Matrix
A Non-Singular matrix is defined as a square matrix whose determinant is not equal to zero and is invertible.
Example of a Non-Singular Matrix
Non-Singular Matrix
⇒ |A| = 8 × 1 - 9 × 5 = 8 - 45 = -37
Symmetric Matrix
A square matrix "A" of any order is defined as a symmetric matrix if the transpose of the matrix is equal to the original matrix itself, i.e., AT = A.
Example of Symmetric Matrix
Symmetric Matrix
Skew Symmetric Matrix
A square matrix "A" of any order is defined as a skew-symmetric matrix if the transpose of the matrix is equal to the negative of the original matrix itself, i.e., AT = -A.
Example of Skew Symmetric Matrix
Symmetric MatrixOrthogonal Matrix
A square matrix whose transpose is equal to its inverse is called Orthogonal Matrix. In an Orthogonal Matrix if AT = A-1 then AAT = I where I is the Identity Matrix.
Example of Orthogonal Matrix
Orthogonal MatrixIdempotent Matrix
An idempotent matrix is a special type of square matrix that remains unchanged when multiplied by itself, i.e., A2 = A.
Example of Idempotent Matrix
Idempotent MatrixNilpotent Matrix
A Nilpotent is a square matrix that when raised to some positive power results in a zero matrix. The least power let's say 'p' for which the matrix yields zero matrices, then it is called the Nilpotent Matrix of power 'p'.
Example of Nilpotent Matrix
Nilpotent MatrixHence, A is a Nilpotent Matrix of index 3.
Periodic Matrix
A periodic matrix is a square matrix that exhibits periodicity, meaning there exists a positive integer p such that when the matrix is raised to the power p+1, it equals the original matrix (Ap+1 = A). If p = 1 then A2 = A it means A is an Idempotent Matrix. Thus we can say that the Idempotent Matrix is a case of the Periodic Matrix.
Example of Periodic Matrix
Periodic MatrixThe above square matrix is a Periodic Matrix of Period 2, where p = 1.
Involuntary Matrix
An involuntary matrix is a special type of square matrix whose inverse is the original matrix itself, i.e., P = P-1, or, in other words, its square is equal to an identity matrix i.e. P2 = I.
Example of Involuntary Matrix
Involuntary MatrixHermitian Matrix
A complex square matrix is called a Hermitian Matrix if the conjugate transpose of the matrix is equal to the original matrix. In this type of matrix, the diagonal elements must be a real number.
Example of Hermitian Matrix
Hermitian MatrixSkew Hermitian Matrix
A complex square matrix is called a Skew Hermitian Matrix if the conjugate transpose of the matrix is equal to the negative of the original matrix. In this type of matrix, the diagonal elements can be either 0 or a complex number but can not be real numbers other than 0.
Example of Skew Hermitian Matrix
Hermitian MatrixBoolean Matrix
The matrix which represents the binary relationship and takes 0 and 1 as its element is called a Boolean Matrix.
Example of Boolean Matrix
Boolean MatrixStochastic Matrix
A square matrix represents probability data, meaning that each element is non-negative, and the sum of the elements in each row is equal to 1. Such a matrix is called a stochastic matrix.
Example of Stochastic Matrix
Stochastic MatrixSummary
Different types of matrices in linear algebra along with their representation is given below.
| Matrix Type | Example |
|---|
| Singleton Matrix | \begin{bmatrix} 1 \end{bmatrix} |
| Null Matrix | \mathbf{O} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} |
| Row Matrix | {R} = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} |
| Column Matrix | \mathbf{C} = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} |
| Horizontal Matrix | \mathbf{H} = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} |
| Vertical Matrix | \mathbf{V} = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} |
| Rectangular Matrix | \mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} |
| Square Matrix | \mathbf{S} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} |
| Diagonal Matrix | {D} = \begin{bmatrix} 1 & 0 \\ 0 & 2 \end{bmatrix} |
| Scalar Matrix | {M} = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} |
| Identity Matrix | \mathbf{I} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} |
| Triangular Matrix | \mathbf{T} = \begin{bmatrix} 1 & 2 \\ 0 & 3 \end{bmatrix} |
| Singular Matrix | |A| = 0; determinant is zero |
| Non-Singular Matrix | |A| ≠0; determinant is not equal to zero |
| Symmetric Matrix | AT = A; square matrix that remains same when its transpose is taken |
| Skew-Symmetric Matrix | AT = -A; square matrix with transpose equal to negative |
| Orthogonal Matrix | Q QT = ln = QT Q |
| Idempotent Matrix | A*A = A |
| Nilpotent Matrix | Ak = 0; where, k ≤ n |
| Periodic Matrix | A(k+1) = A |
| Involutory Matrix | A*A = I |
| Hermitian Matrix | A = \overline{A^{\mathsf{T}}} |
| Skew Hermitian Matrix | If A is a skew-hermitian matrix, then A* = -A |
| Boolean Matrix | \mathbf{B} = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}; element is either 0 or 1. |
| Stochastic Matrix | \mathbf{B} = \begin{bmatrix} 1 & 2.2 \\ 0 & 14 \end{bmatrix}; all elements are non-negative. |
Practice Problem Based on Types of Matrix
Question 1. Given the following matrix, is it a Singular or Non-Singular matrix? B = \begin{pmatrix} 5 & 2 \\1 & 2 \end{pmatrix} .
Question 2. Given the matrix A = \begin{pmatrix} 1 & 3 & 0 \\2 & 4 & 1 \\1 & 1 & 2 \end{pmatrix} Is matrix A symmetric or skew-symmetric?
Question 3. Given the matrix A = \begin{pmatrix} 1 & 3 & 0 \\2 & 4 & 1 \\1 & 1 & 2 \end{pmatrix} Find the determinant of matrix A.
Question 4. What type of matrix has its transpose equal to its inverse?
Question 5. What type of matrix has all its elements as zero?
Question 6. Which matrix has the same elements along the diagonal and zero elsewhere?
Answer :-
- non-singular.
- neither symmetric nor skew-symmetric.
- -2.
- Orthogonal Matrix.
- Null Matrix.
- Scalar Matrix.
Similar Reads
Algebra in Math - Definition, Branches, Basics and Examples Algebra is the branch of mathematics with the following properties.Deals with symbols (or variables) and rules for manipulating these symbols. Elementary (Taught in Schools) Algebra mainly deals with variables and operations like sum, power, subtraction, etc. For example, x + 10 = 100, x2 - 2x + 1 =
4 min read
Basics of Algebra
Algebraic Expression
Algebra Practice Questions Easy LevelAlgebra questions basically involve modeling word problems into equations and then solving them. Some of the very basic formulae that come in handy while solving algebra questions are : (a + b) 2 = a 2 + b 2 + 2 a b(a - b) 2 = a 2 + b 2 - 2 a b(a + b) 2 - (a - b) 2 = 4 a b(a + b) 2 + (a - b) 2 = 2 (
3 min read
Algebraic IdentitiesAlgebraic Identities are fundamental equations in algebra where the left-hand side of the equation is always equal to the right-hand side, regardless of the values of the variables involved. These identities play a crucial role in simplifying algebraic computations and are essential for solving vari
14 min read
Factorization of PolynomialFactorization in mathematics refers to the process of expressing a number or an algebraic expression as a product of simpler factors. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, and we can express 12 as 12 = 1 × 12, 2 × 6, or 4 × 3.Similarly, factorization of polynomials involves expre
10 min read
Division of Algebraic ExpressionsDivision of algebraic expressions is a key operation in algebra. It is essential for simplifying expressions and solving equations. It is used to perform polynomial long division or synthetic division. Division of algebraic expressions is performed as as division on two whole numbers or fractions. I
6 min read
Polynomials
Polynomials| Degree | Types | Properties and ExamplesPolynomials are mathematical expressions made up of variables (often represented by letters like x, y, etc.), constants (like numbers), and exponents (which are non-negative integers). These expressions are combined using addition, subtraction, and multiplication operations.A polynomial can have one
9 min read
Types of Polynomials (Based on Terms and Degrees)Types of Polynomials: In mathematics, an algebraic expression is an expression built up from integer constants, variables, and algebraic operations. There are mainly four types of polynomials based on degree-constant polynomial (zero degree), linear polynomial ( 1st degree), quadratic polynomial (2n
9 min read
Zeros of PolynomialZeros of a Polynomial are those real, imaginary, or complex values when put in the polynomial instead of a variable, the result becomes zero (as the name suggests zero as well). Polynomials are used to model some physical phenomena happening in real life, they are very useful in describing situation
13 min read
Geometrical meaning of the Zeroes of a PolynomialAn algebraic identity is an equality that holds for any value of its variables. They are generally used in the factorization of polynomials or simplification of algebraic calculations. A polynomial is just a bunch of algebraic terms added together, for example, p(x) = 4x + 1 is a degree-1 polynomial
8 min read
Multiplying Polynomials WorksheetA polynomial is an algebraic expression consisting of variables and coefficients. We can perform various operations on polynomials, including addition, subtraction, multiplication, and division. This worksheet focuses on multiplying polynomials using different methods.Read More: Multiplying Polynomi
4 min read
Dividing Polynomials | Long Division | Synthetic Division | Factorization MethodsDividing Polynomials in maths is an arithmetic operation in which one polynomial is divided by another polynomial, where the divisor polynomial must have a degree less than or equal to the Dividend Polynomial otherwise division of polynomial can't take place. The most general form of a polynomial is
13 min read
Division Algorithm for PolynomialsPolynomials are those algebraic expressions that contain variables, coefficients, and constants. For Instance, in the polynomial 8x2 + 3z - 7, in this polynomial, 8,3 are the coefficients, x and z are the variables, and 7 is the constant. Just as simple Mathematical operations are applied on numbers
5 min read
Division Algorithm Problems and SolutionsPolynomials are made up of algebraic expressions with different degrees. Degree-one polynomials are called linear polynomials, degree-two are called quadratic and degree-three are called cubic polynomials. Zeros of these polynomials are the points where these polynomials become zero. Sometimes it ha
6 min read
Remainder TheoremThe Remainder Theorem is a simple yet powerful tool in algebra that helps you quickly find the remainder when dividing a polynomial by a linear polynomial, such as (x - a). Instead of performing long or synthetic division, you can use this theorem to substitute the polynomial and get the remainder d
8 min read
Factor TheoremFactor theorem is used for finding the roots of the given polynomial. This theorem is very helpful in finding the factors of the polynomial equation without actually solving them.According to the factor theorem, for any polynomial f(x) of degree n ≥ 1 a linear polynomial (x - a) is the factor of the
10 min read
Algebraic Identities of PolynomialsAlgebraic identities are equations that hold true for all values of the variables involved. In the context of polynomials, these identities are particularly useful for simplifying expressions and solving equations.Algebraic Identities of PolynomialsWhat are Algebraic Identities?Algebraic Identities
9 min read
Factoring PolynomialsFactoring Polynomials: A basic algebraic concept called factoring polynomials involves breaking down a polynomial equation into simpler parts. Factoring can be used to solve equations, simplify complicated expressions, and locate the roots or zeros of polynomial functions. In several fields of math
9 min read
Relationship between Zeroes and Coefficients of a PolynomialPolynomials are algebraic expressions with constants and variables that can be linear i.e. the highest power o the variable is one, quadratic and others. The zeros of the polynomials are the values of the variable (say x) that on substituting in the polynomial give the answer as zero. While the coef
9 min read
Linear Equations
Linear Equations in One VariableLinear equation in one variable is the equation that is used for representing the conditions that are dependent on one variable. It is a linear equation i.e. the equation in which the degree of the equation is one, and it only has one variable.A linear equation in one variable is a mathematical stat
7 min read
Solving Linear Equations with Variable on both SidesEquations consist of two main components: variables and numbers. Understanding the relationship between these components and how to manipulate them is essential for solving equations.Variable: A variable is a symbol (often a letter like x, y, or z) that represents an unknown or changing quantity.Num
6 min read
Graphical Methods of Solving Pair of Linear Equations in Two VariablesA system of linear equations is just a pair of two lines that may or may not intersect. The graph of a linear equation is a line. There are various methods that can be used to solve two linear equations, for example, Substitution Method, Elimination Method, etc. An easy-to-understand and beginner-fr
8 min read
Reducing Equations to Simpler Form | Class 8 MathsReducing equations is a method used to simplify complex equations into a more manageable form. This technique is particularly useful when dealing with non-linear equations, which cannot always be solved directly. By applying specific mathematical operations, such as cross-multiplication, these equat
6 min read
Linear Equation in Two VariablesLinear Equation in Two Variables: A Linear equation is defined as an equation with the maximum degree of one only, for example, ax = b can be referred to as a linear equation, and when a Linear equation in two variables comes into the picture, it means that the entire equation has 2 variables presen
9 min read
Graph of Linear Equations in Two VariablesLinear equations are the first-order equations, i.e. the equations of degree 1. The equations which are used to define any straight line are linear, they are represented as, x + k = 0; These equations have a unique solution and can be represented on number lines very easily. Let's look at linear e
5 min read
Equations of Lines Parallel to the x-axis and y-axisLinear Equations allow us to explain a lot of physical phenomena happening around us. For example, A train running between two stations at a constant speed, the speed of a falling object. Even the straight lines we draw on paper can be represented in form of linear equations mathematically. A linear
6 min read
Pair of Linear Equations in Two VariablesLinear Equation in two variables are equations with only two variables and the exponent of the variable is 1. This system of equations can have a unique solution, no solution, or an infinite solution according to the given initial condition. Linear equations are used to describe a relationship betwe
11 min read
Number of Solutions to a System of Equations AlgebraicallyA statement that two mathematical expressions of one or more variables are identical is called an equation. Linear equations are those in which the powers of all the variables concerned are equal. A linear equation's degree is always one. A solution of the simultaneous pair of linear equations is a
7 min read
Solve the Linear Equation using Substitution MethodA linear equation is an equation where the highest power of the variable is always 1. Its graph is always a straight line. A linear equation in one variable has only one unknown with a degree of 1, such as:3x + 4 = 02y = 8m + n = 54a – 3b + c = 7x/2 = 8There are mainly two methods for solving simult
10 min read
Cross Multiplication MethodCross multiplication method is one of the basic methods in mathematics that is used to solve the linear equations in two variables. It is one of the easiest to solve a pair of linear equations in two variables. Suppose we have a pair of linear equations in two variables, i.e. a1x + b1y = -c1 and a2
9 min read
Equations Reducible to Linear FormEquations Reducible to Linear Form" refers to equations that can be transformed or rewritten into a linear equation. These equations typically involve variables raised to powers other than 1, such as squared terms, cubed terms, or higher. By applying suitable substitutions or transformations, these
9 min read
Quadratic Equations
Quadratic EquationsA Quadratic equation is a second-degree polynomial equation that can be represented as ax2 + bx + c = 0. In this equation, x is an unknown variable, a, b, and c are constants, and a is not equal to 0. The solutions of a quadratic equation are known as its roots. These roots can be found using method
12 min read
Solving Quadratic EquationsA quadratic equation, typically in the form ax² + bx + c = 0, can be solved using different methods including factoring, completing the square, quadratic formula, and the graph method. While Solving Quadratic Equations we try to find a solution that represent the points where this the condition Q(x)
8 min read
Roots of Quadratic EquationThe roots of a quadratic equation are the values of x that satisfy the equation. The roots of a quadratic equation are also called zeros of a quadratic equation. A quadratic equation is generally in the form: ax2 + bx + c = 0Where:a, b, and c are constants (with a ≠0).x represents the variable.Root
13 min read
Cubic Equations
Sequence and Series
Arithmetic Progression in MathsArithmetic Progression (AP) or Arithmetic Sequence is simply a sequence of numbers such that the difference between any two consecutive terms is constant.Some Real World Examples of APNatural Numbers: 1, 2, 3, 4, 5, . . . with a common difference 1Even Numbers: 2, 4, 6, 8, 10, . . . with a common di
3 min read
Arithmetic SeriesAn arithmetic series is the sum of the terms of an arithmetic sequence, where an arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant. Or we can say that an arithmetic progression can be defined as a sequence of numbers in which for every pair of
5 min read
Arithmetic SequenceAn arithmetic sequence or progression is defined as a sequence of numbers in which the difference between one term and the next term remains constant.For example: the given below sequence has a common difference of 1.1 2 3 4 5 . . . n ⇑ ⇑ ⇑ ⇑ ⇑ . . . 1st 2nd 3rd 4th 5th . . . nth TermsThe Arithmetic
8 min read
Program to Check Geometric ProgressionA sequence of numbers is called a Geometric progression if the ratio of any two consecutive terms is always the same.In simple terms, A geometric series is a list of numbers where each number, or term, is found by multiplying the previous term by a common ratio r. The general form of Geometric Progr
6 min read
Geometric SeriesIn a Geometric Series, every next term is the multiplication of its Previous term by a certain constant, and depending upon the value of the constant, the Series may increase or decrease.Geometric Sequence is given as: a, ar, ar2, ar3, ar4,..... {Infinite Sequence}a, ar, ar2, ar3, ar4, ....... arn {
3 min read
Set Theory
Representation of a SetSets are defined as collections of well-defined data. In Math, a Set is a tool that helps to classify and collect data belonging to the same category. Even though the elements used in sets are all different from each other, they are all similar as they belong to one group. For instance, a set of dif
8 min read
Types Of SetsIn mathematics, a set is defined as a well-defined collection of distinct elements that share a common property. These elements— like numbers, letters, or even other sets are listed in curly brackets "{ }" and represented by capital letters. For example, a set can include days of the week. The diffe
13 min read
Universal SetsUniversal Set is a set that has all the elements associated with a given set, without any repetition. Suppose we have two sets P = {1, 3, 5} and Q = {2, 4, 6} then the universal set of P and Q is U = {1, 2, 3, 4, 5, 6}. We generally use U to denote universal sets. Universal Set is a type of set that
6 min read
Venn DiagramVenn diagrams are visual tools used to show relationships between different sets. They use overlapping circles to represent how sets intersect, share elements, or stay separate. These diagrams help categorize items, making it easier to understand similarities and differences. In mathematics, Venn di
14 min read
Operations on SetsSets are fundamental in mathematics and are collections of distinct objects, considered as a whole. In this article, we will explore the basic operations you can perform on sets, such as union, intersection, difference, and complement. These operations help us understand how sets interact with each
15+ min read
Union of SetsUnion of two sets means finding a set containing all the values in both sets. It is denoted using the symbol '∪' and is read as the union. Example 1:If A = {1, 3. 5. 7} and B = {1, 2, 3} then A∪B is read as A union B and its value is,A∪B = {1, 2, 3, 5, 7}Example 2:If A = {1, 3. 5.7} and B = {2, 4} t
12 min read
Cartesian Product of SetsThe term 'product' mathematically refers to the result obtained when two or more values are multiplied together. For example, 45 is the product of 9 and 5.To understand the Cartesian product of sets, one must first be familiar with basic set operations such as union and intersection, which are appli
7 min read
Relations and Functions
Relations and FunctionsIn mathematics, we often deal with sets of numbers or objects and the ways they are connected. Two important concepts that help us describe these connections are relations and functions.A relation is simply a connection between two sets of objects. Think of it as a rule that pairs elements from one
3 min read
Intoduction to Functions | Representation | Types | ExamplesA function is a special relation or method connecting each member of set A to a unique member of set B via a defined relation. Set A is called the domain and set B is called the co-domain of the function. A function in mathematics from set A to set B is defined as,f = {(a,b)| ∀ a ∈ A, b ∈ B}A functi
14 min read
Types of FunctionsFunctions are defined as the relations which give a particular output for a particular input value. A function has a domain and codomain (range). f(x) usually denotes a function where x is the input of the function. In general, a function is written as y = f(x).A function is a relation between two s
15 min read
Composite functions - Relations and functionsLet f : A->B and g : B->C be two functions. Then the composition of f and g, denoted by g o f, is defined as the function g o f : A->C given by g o f (x) = g{f(x)}, ∀ x ∈ A. Clearly, dom(g o f) = dom(f). Also, g o f is defined only when range(f) is a subset of dom(g). Evaluating composite f
5 min read
Invertible FunctionsAs the name suggests Invertible means "inverse", and Invertible function means the inverse of the function. Invertible functions, in the most general sense, are functions that "reverse" each other. For example, if f takes a to b, then the inverse, f-1, must take b to a. Table of ContentInvertible Fu
15 min read
Composition of FunctionsThe composition of functions is a process where you combine two functions into a new function. Specifically, it involves applying one function to the result of another function. In simpler terms, the output of one function becomes the input for the other function.Mathematically, the composition of t
11 min read
Inverse Functions | Definition, Condition for Inverse and ExamplesInverse Functions are an important concept in mathematics. An inverse function basically reverses the effect of the original function. If you apply a function to a number and then apply its inverse, you get back the original number. For example, if a function turns 2 into 5, the inverse function wil
7 min read
Verifying Inverse Functions by CompositionA function can be seen as a mathematical formula or a machine that throws output when an input is given. The output is usually some processed version of the input. Function's inverses can be seen as the operations which give us the input back on giving them the output. In other words, inverse functi
5 min read
Domain and Range of a FunctionIn mathematics, a function represents a relationship between a set of inputs and their corresponding outputs. Functions are fundamental in various fields, from algebra to calculus and beyond, as they help model relationships and solve real-world problems.A function represents a relationship between
15 min read
Piecewise FunctionPiecewise Function is a function that behaves differently for different types of input. As we know a function is a mathematical object which associates each input with exactly one output. For example: If a function takes on any input and gives the output as 3. It can be represented mathematically as
11 min read