A Ternary Tree is a special type of tree data structure. Unlike a regular binary tree where each node can have up to two child nodes. The article explains the basic structure and properties of ternary trees, such as the number of possible children per node, tree height, and node depth. It also discusses why ternary trees can be useful, highlighting applications in areas like string searching and database indexing. It also introduces some common problems and algorithms related to ternary trees.
What is a Ternary Tree?
A Ternary Tree is a type of tree data structure where each node can have up to three child nodes. This is different from a binary tree, where each node can have at most two child nodes. In a ternary tree, the first child node is called the "left" child, the second child node is called the "middle" child, and the third child node is called the "right" child.
Basic Structure of a Ternary Tree
In a ternary tree:
- Each node has three possible children: a left child, a middle child, and a right child.
- The nodes are connected by edges that represent the parent-child relationships.
Here's a simple visualization of a ternary tree:
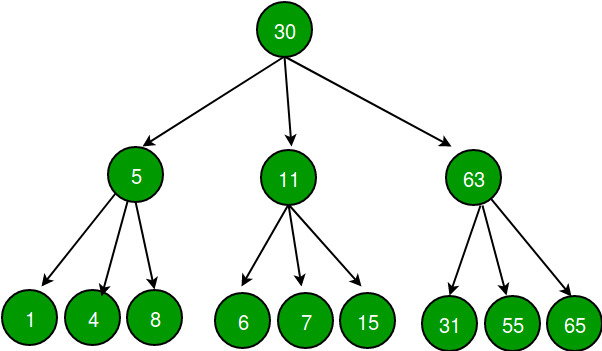 Ternary Tree
Ternary TreeProperties of Ternary Trees
- Children Count: Each node in a ternary tree can have zero, one, two, or three children.
- Height: The height of a ternary tree is the length of the longest path from the root to a leaf. A leaf is a node with no children.
- Depth: The depth of a node is the number of edges from the root to the node.
Why Use a Ternary Tree?
Ternary trees are useful in specific scenarios where more than two children per node are beneficial. Here are some common applications:
- Ternary Search Trees: These are specialized ternary trees used for storing and searching strings. They combine the advantages of binary search trees and digital search tries, making them efficient for certain types of string search operations.
- Multi-way Trees: In databases and file systems, multi-way trees (like B-trees) generalize ternary trees to have more than three children, but the concept starts with understanding ternary trees.
Basic Operations on a Ternary Tree
- Insertion: Adding a new node to the tree.
- Deletion: Removing a node from the tree.
- Traversal: Visiting all the nodes in the tree in a specific order. Common traversal methods include:
- Pre-order Traversal: Visit the root, then recursively visit the left, middle, and right subtrees.
- In-order Traversal: Recursively visit the left subtree, visit the root, then the middle subtree, and finally the right subtree.
- Post-order Traversal: Recursively visit the left, middle, and right subtrees, then visit the root.
Applications of Ternary Trees
Here are a few key applications of ternary trees:
- Ternary Search Trees: Ternary search trees are specialized ternary trees used for efficient storage and searching of strings. They combine the advantages of binary search trees and digital search tries, making them effective for certain string-based operations.
- Multi-way Trees: In databases and file systems, multi-way trees like B-trees generalize the concept of ternary trees to have more than three children per node. Understanding the structure and properties of ternary trees is a foundational step for these more complex multi-way tree data structures.
- Text Auto-completion: Ternary search trees can be leveraged to implement text auto-completion features, where suggestions are provided as the user types. The tree structure allows for efficient prefix-based lookups and string traversal.
- Prefix-based Indexing: Similar to auto-completion, ternary search trees can be used to build prefix-based indexes for quickly finding words or phrases that match a given prefix, which is useful in search engines and natural language processing applications.
Problems on Ternary Tree:
- Create a Doubly Linked List from a Ternary Tree
- Ternary Search Tree
- Ternary Search Tree (Deletion)
- Longest word in ternary search tree
- How to implement text Auto-complete feature using Ternary Search Tree
Similar Reads
What is Binary Tree? A binary tree is a type of tree data structure in which each node can have at most two child nodes, known as the left child and the right child. Each node of the tree consists of - data and pointers to the left and the right child. Example of Binary TreeProperties of a Binary Tree: The following are
3 min read
Ternary Search Tree A ternary search tree is a special trie data structure where the child nodes of a standard trie are ordered as a binary search tree. Representation of ternary search trees: Unlike trie(standard) data structure where each node contains 26 pointers for its children, each node in a ternary search tree
13 min read
What is Binary Search Tree A binary search tree (BST) is a binary tree in which the left subtree of a node contains only nodes with less value and the right subtree of a node contains only nodes with values greater than it. Binary Search TreeCharacteristics of Binary Search Tree: The properties of a binary search tree are as
3 min read
What is Full Binary Tree? A full binary tree is a type of binary tree in which every node has either zero or two children. Full Binary Tree exampleProperties of Full Binary Tree: Let i be the number of internal nodes, n be the total number of nodes, l be the number of leaf nodes and h be the total number of levels The number
2 min read
Why use Ternary search tree (TST)? Ternary search tree (TST) is a very popular data structure used in the problem solving becaus of following reasons: First, they offer efficient search operations, particularly for strings, with lookup times typically on the order of O(log n), where n is the length of the search key. This makes them
2 min read
Longest word in ternary search tree Given a set of words represented in a ternary search tree, find the length of largest word among them. Examples: Input : {"Prakriti", "Raghav", "Rashi", "Sunidhi"} Output : Length of largest word in ternary search tree is: 8 Input : {"Boats", "Boat", "But", "Best"} Output : Length of largest word in
11 min read