Complexity of algorithms
Download as PPTX, PDF1 like49 views
Quicksort is described including its Java source code, time complexity analysis, and optimizations. It works by partitioning an array around pivots and recursively sorting the subarrays. The basic algorithm runs in O(n log n) time on average but can degrade to O(n^2). Optimizations like insertion sort for small subproblems and dual pivots are tested, with dual pivots performing best in testing.
![STABILITY OF QUICKSORT
Because of the way elements within the partitioning are
divided into subsections, elements with the same key
can change their original order.
Here is a simple example:
The array [7, 8, 7, 2, 6] should be partitioned with the
pivot strategy "right element". (We marked the second 7
as 7' to distinguish it from the first one).](https://image.slidesharecdn.com/complexityofalgorithms-210517121201/85/Complexity-of-algorithms-28-320.jpg)
Complexity of algorithms
- 1. This Presentation: • Describes the Quicksort algorithm, • Shows its Java source code, • Explains how to derive its time complexity, • Tests whether the performance of the Java implementation matches the expected runtime behavior, • Introduces various algorithm optimizations (combination with Insertion Sort and Dual-Pivot Quicksort) • Measures and compares their speed. • Quicksort-Algorithm • Source Code • Time Complexity
- 2. ANIMATED VISUALIZATION OF THE QUICKSORT ALGORITHM. THE HORIZONTAL LINES ARE PIVOT VALUES. Class Sorting algorithm Worst-case performance O(n 2 ) Best-case performance O(n log n) (simple partition) or O(n) (three-way partition and equal keys) Average performance O(n log n) Worst-case space complexity O(n) auxiliary (naive) O(log n) auxiliary (Hoare 1962)
- 3. Quicksort Algorithm Quicksort works according to the "divide and conquer" principle: The subarrays to the left and right of the pivot element are still unsorted after partitioning
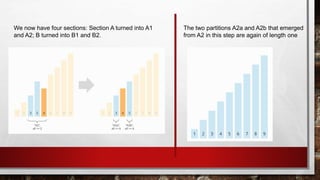
- 4. We now have four sections: Section A turned into A1 and A2; B turned into B1 and B2. The two partitions A2a and A2b that emerged from A2 in this step are again of length one
- 5. QUICKSORT PARTITIONING • In the example from above this works as follows: • The first element from the left, which is larger than pivot element 6, is 7. • The first element from the right, which is smaller than the 6, is the 4. • The 7 and the 4 are swapped. We continue searching and find the 8 from the left (the 1 is already on the correct side) and the 5 from the right (the 9 is also already on the correct side). We swap 8 and 5:
- 6. Now the left and right search positions meet at 2. The swapping ends here To put the pivot element at the beginning of the right partition, we swap the 8 with the 6:
- 7. THE PIVOT ELEMENT • Advantage of the "last element" pivot strategy • Disadvantage of the "last element" pivot strategy • Alternative pivot strategies The partitioning is complete: The 6 is in the correct position, the numbers to the left are smaller, and the numbers to the right are larger. So, we have reached the state that was shown in the previous section after the first partitioning:
- 8. QUICKSORT JAVA SOURCE CODE
- 9. QUICKSORT TIME COMPLEXITY Best-Case Time Complexity
- 10. The best-case time complexity of Quicksort is O(n log n)
- 11. AVERAGE-CASE TIME COMPLEXITY Worst-case Time Complexity The worst-case time complexity of Quicksort is O(n²)
- 12. JAVA QUICKSORT RUNTIME • It sorts arrays of sizes 1,024, 2,048, 4,096, etc. Up to a maximum of 536,870,912 (= 229), but aborts if a single sorting process takes 20 seconds or longer. • It applies the sorting algorithm to unsorted input data and input data sorted in ascending and descending order. • It first runs two warmup phases to allow the hotspot to optimize the code. • The process is repeated until the process is killed.
- 13. RUNTIME MEASUREMENT OF THE QUICKSORT ALGORITHM VARIANTS • The simple algorithm is the fastest. • For all algorithm variants, the pivot strategy right is fastest, closely followed by middle, then median with a slightly larger distance (the overhead is higher than the gain here). RANDOM is slowest (generating random numbers is expensive). • For all pivot strategies, variant 1 is the fastest, variant 3 the second fastest, and variant 2 is the slowest.
- 14. RUNTIME MEASUREMENTS FOR DIFFERENT PIVOT STRATEGIES AND ARRAY SIZES
- 15. The data shows: For both unsorted and sorted input data, doubling the array size requires slightly more than twice the time. This corresponds to the expected quasilinear runtime – O(n log n).
- 17. OVERVIEW OF ALL MEASUREMENT RESULTS Here you can find the measurement results again as a diagram (We have omitted input data sorted in descending order for clarity):
- 18. QUICKSORT OPTIMIZED: COMBINATION WITH INSERTION SORT The source code changes compared to the standard quicksort are very straightforward and are limited to the quicksort() method. Here is the method from the standard algorithm once again:
- 19. And here is the optimized version. The variables insertionSort and quicksort are instances of the respective sorting algorithm. Only the code block commented with "Threshold for insertion sort reached?" has been added in the middle of the method:
- 20. QUICKSORT/INSERTION SORT PERFORMANCE The CompareImprovedQuickSort program measures the time needed to sort about 5.5 million elements at different thresholds for switching to Insertion Sort.
- 21. HERE ARE THE MEASUREMENTS IN GRAPHICAL REPRESENTATION:
- 22. DUAL-PIVOT QUICKSORT The following diagram shows an example of partitioning with two pivot elements at the "thirds" positions: Dual- Pivot Quicksort (with additional optimizations) is used in the JDK by the method Arrays.sort())
- 23. DUAL-PIVOT QUICKSORT SOURCE CODE Compared to the regular algorithm, the quicksort() method calls itself recursively not for two but three partitions:
- 24. Then again, two search pointers run over the array from left and right and compare and swap the elements to be eventually divided into three partitions. How exactly they do this can be read reasonably well from the source code.
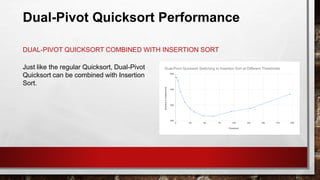
- 26. DUAL-PIVOT QUICKSORT COMBINED WITH INSERTION SORT Just like the regular Quicksort, Dual-Pivot Quicksort can be combined with Insertion Sort. Dual-Pivot Quicksort Performance
- 27. COMPARING ALL QUICKSORT OPTIMIZATIONS
- 28. STABILITY OF QUICKSORT Because of the way elements within the partitioning are divided into subsections, elements with the same key can change their original order. Here is a simple example: The array [7, 8, 7, 2, 6] should be partitioned with the pivot strategy "right element". (We marked the second 7 as 7' to distinguish it from the first one).
- 29. The first element from the left that is greater than 6 is the first 7. The first 7 is no longer ahead, but behind the second 7
- 30. OPTIMIZATION Two other important optimizations, also widely used in practice, are: 1. Make sure at most O(log n) space is used. 2. When the number of elements is less than the threshold k, simply stop; then after the whole array has been processed, perform insertion sort on it
- 31. CONCLUSION Quicksort is an efficient, unstable sorting algorithm with time complexity of o(n log n) in the best and average case and o(n²) in the worst case.
- 32. THANKS FOR YOUR ATTENTION ! Prepared by: Jasur Ahmadov