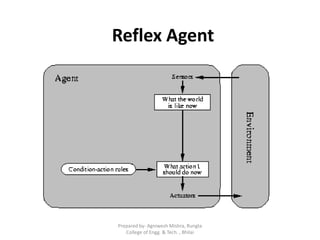
The document provides an overview of knowledge representation techniques. It discusses propositional logic, including syntax, semantics, and inference rules. Propositional logic uses atomic statements that can be true or false, connected with operators like AND and OR. Well-formed formulas and normal forms are explained. Forward and backward chaining for rule-based reasoning are summarized. Examples are provided to illustrate various concepts.























































![Solution
6. Everyone is loyal to someone.
x: y: LoyalTo(x,y)
7. People only try to assassinate rulers they aren't loyal to.
x: y: Person(x) ^ Ruler(y) ^ TryAssassinate(x,y) ¬LoyalTo(x,y)]
8. Marcus tried to assassinate Caesar.
TryAssassinate(Marcus, Caesar)
9. All men are people.
x: Men(x) People(x)
Prepared by- Agniwesh Mishra, Rungta
College of Engg. & Tech. , Bhilai](https://image.slidesharecdn.com/aiunit2-180129180409/85/Artificial-Intelligence-Notes-Unit-2-56-320.jpg)







![Example 1
Everybody loves somebody.
x: y: (Person(x) ^ Person(y)) Loves(x,y)]
Converted to
x: (Person(x) ^ Person f(x)) Loves(x,f(x))]
Where f(x) specifies the person that x loves.
Prepared by- Agniwesh Mishra, Rungta
College of Engg. & Tech. , Bhilai](https://image.slidesharecdn.com/aiunit2-180129180409/85/Artificial-Intelligence-Notes-Unit-2-64-320.jpg)
![Clausal Form
• A formula is said to be in clausal form if it is of the form:
∀x1 ∀x2 … ∀xn [C1 ∧ C2 ∧ … ∧ Ck]. „
• All first-order logic formulas can be converted to clausal
form.
Prepared by- Agniwesh Mishra, Rungta
College of Engg. & Tech. , Bhilai](https://image.slidesharecdn.com/aiunit2-180129180409/85/Artificial-Intelligence-Notes-Unit-2-65-320.jpg)
![Equivalent Logical Expressions
i. ~(~F) = F (Double Negation)
ii. F & G = G & F, F V G = G V F (Commutativity)
iii. (F & G) & H = F & (G & H), (F V G) V H = F V (G V H) (Associativity)
iv. F V (G & H) = (F V G) & (F V H), F & (G V H) = (F & G) V (F & H)
(Distributivity)
v. ~(F & G) = ~F V ~G, ~(F V G) = ~F & ~G (De Morgan)
vi. F G = ~F V G
vii. F G = (~F V G) & (~G V F)
viii. x F[x] V G = x (F[x] V G )
ix. x F[x] V G = x (F[x] V G )
x. x F[x] & G = x (F[x] & G )
xi. x F[x] & G = x (F[x] & G )
Prepared by- Agniwesh Mishra, Rungta
College of Engg. & Tech. , Bhilai](https://image.slidesharecdn.com/aiunit2-180129180409/85/Artificial-Intelligence-Notes-Unit-2-66-320.jpg)
![Equivalent Logical Expressions...
xii. ~(x) F[x] = x (~F[x])
xiii. ~(x) F[x] = x (~F[x])
xiv. x F[x] & x G[x] = x (F[x] & G[x])
xv. x F[x] & x G[x] = x (F[x] & G[x])
Prepared by- Agniwesh Mishra, Rungta
College of Engg. & Tech. , Bhilai](https://image.slidesharecdn.com/aiunit2-180129180409/85/Artificial-Intelligence-Notes-Unit-2-67-320.jpg)






![Convert it into FOPL
i. All lectures are determined.
x: Lecturer(x) Determined(x)
ii. Any one who is determined and intelligent will give good
service.
x: Determined(x) ^ Intelligent(x)Givegoodservice(x)]
iii. Mary is an intelligent lecturer.
Lecturer(mary)
Intelligent(mary)
Prepared by- Agniwesh Mishra, Rungta
College of Engg. & Tech. , Bhilai](https://image.slidesharecdn.com/aiunit2-180129180409/85/Artificial-Intelligence-Notes-Unit-2-74-320.jpg)




![Example of FOPL
6. Everyone is loyal to someone.
x: y: LoyalTo(x,y)
7. People only try to assassinate rulers they aren't loyal to.
x: y: Person(x) ^ Ruler(y) ^ TryAssassinate(x,y) ¬LoyalTo(x,y)]
8. Marcus tried to assassinate Caesar.
TryAssassinate(Marcus, Caesar)
9. All men are people.
x: Men(x) People(x)
Prepared by- Agniwesh Mishra, Rungta
College of Engg. & Tech. , Bhilai](https://image.slidesharecdn.com/aiunit2-180129180409/85/Artificial-Intelligence-Notes-Unit-2-79-320.jpg)