Multi Objective Optimization
- 1. CE 588 Structural Optimization Multi-Objective Optimization Instructor: Y.Doç.Dr. NİLDEM TAYŞİ 3/12/2013 Samadar Salim Majeed
- 2. Introduction Is an area of multiple criteria decision making, that is concerned with mathmatical optimization problem involving more than one objective function to be optimized simultaneously. Most real-world engineering optimization problems are multi-Objective in nature Objectives are often conflicting Performance vs. Silicon area Quality vs. Cost Efficiency vs. Portability The notion of ”optimum” has to be redefined
- 3. Multiobjective optimization (multicriteria, multiperformance, vector optimization or Pareto optimization ) Find a vector of decision variables which satisfies constraints and optimizes a vector function whose elements represent the objective functions Objectives are usually in conflict with each other Optimize: finding solutions which would give the values of all the objective functions acceptable to the designer
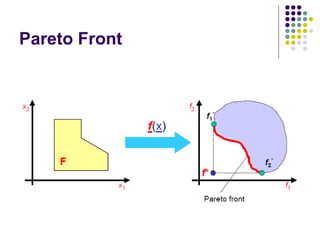
- 10. Pareto Front
- 12. Multi-Objective Optimization Classic Methods : 1- Weighted Sum Method 2- Constraint method 3- Weighted Metric Methods 4- Rotated Weighted Metric Method 5- Benson’s Method 5- Value Function Method Currently an Evolutionary Algorithm Methods are Used For MOOP
- 13. Multi-Objective Optimization All the problems that we have considered in this class have been comprised of a single objective function with perhaps multiple constraints and design variables. Minimize Subject To: F (x) g ( x) ≤ 0 ....
- 14. Multi-Objective Optimization In such a case, the problem has a 1 dimensional performance space and the optimum point is the one that is the furthest toward the desired extreme. Optimum 0 - + F
- 15. Multi-Objective Optimization What happens when it is necessary (or at least desirable) to optimize with respect to more than one criteria? Now we have additional dimensions in our performance space and we are seeking the best we can get for all dimensions simultaneously. What does that mean “best in all dimensions”?
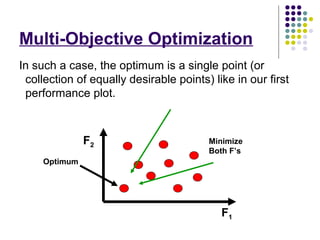
- 16. Multi-Objective Optimization Consider the following 2D performance space: F2 Minimize Both F’s Optimum F1
- 17. Multi-Objective Optimization But what happens in a case like this: F2 Minimize Both F’s Optimum? Optimum? F1
- 18. Multi-Objective Optimization The one on the left is better with respect to F1 but worse with respect to F2. And the one on the right is better with respect to F2 and worse with respect to F1. How does one wind up in such peril?
- 19. Multi-Objective Optimization That depends on the relationships that exist between the various objectives. There are 3 possible interactions that may exist between objectives in a multi-objective optimization problem: 1. Cooperation 2. Competition 3. No Relationship
- 20. Multi-Objective Optimization What defines a relationship between objectives? How can I recognize that two objectives have any relationship at all? The relationship between two objectives is defined by the variables that they have in common. Two objectives will fight for control of common design variables throughout a multi-objective design optimization process.
- 21. Multi-Objective Optimization Just how vicious the fight is depends on what type of interaction exists (of the 3 we mentioned). Let’s consider the 1st case of cooperation. Two objectives are said to “cooperate” if they both wish to drive all their common variables in the same direction (pretty much all the time). In such a case, betterment of one objective typically accompanies betterment of the other.
- 22. Multi-Objective Optimization In such a case, the optimum is a single point (or collection of equally desirable points) like in our first performance plot. F2 Minimize Both F’s Optimum F1
- 23. Multi-Objective Optimization Now let’s consider the 2nd case of competition. Two objectives are said to “compete” if they wish to drive at least some of their common variables in different directions. In such a case, betterment of one objective typically comes at the expense of the other. This is the most interesting case.
- 24. Multi-Objective Optimization In such a case, the optimum is no longer a single point but a collection of points called the Pareto Set. Optimality criterion for optimization problems with multiple objectives. A state (set of parameters) is said to be Pareto optimal if there is no other state dominating the state with respect to a set of objective functions. State A dominates state B if A is better than B in at least one objective function and not worse with respect to all other objective functions.
- 25. Multi-Objective Optimization So let’s take a look at this: F2 Minimize Both F’s F1
- 26. Multi-Objective Optimization For completeness, we will now consider the case in which there is no relationship between two objectives. When do you think such a thing might occur? Clearly this only occurs when the two objectives have no design variables in common (each is a function of a different subset of the design variables and the 2 subsets have a null intersection).
- 27. Multi-Objective Optimization In such a case, we are free to optimize each function individually to determine our optimal design configuration. That is why this case is desirable but uninteresting. So back to competing objectives.
- 28. Multi-Objective Optimization Now that we know what we are looking for, that is, the set of non-dominated designs, how are we going to go about generating it? The most common way to generate points along a Pareto frontier is to use a weighted sum approach. Consider the following example:
- 29. Multi-Objective Optimization Suppose I wish to minimize both of the following functions simultaneously: F1 = 750x1+60(25-x1) x2+45(25- x1)(25- x2) F2 = (25- x1) x2 For the typical weighted sum approach, I would assign a weight to each function such that: w1 + w2 = 1 and w1 , w2 ≥ 0
- 30. Multi-Objective Optimization I would then combine the two functions into a single function as follows and solve: FT = ∑ wi Fi i = w1 F1 + w2 F2
- 31. Multi-Objective Optimization The net effect of our weighted sum approach is to convert a multiple objective problem into a single objective problem. But this will only provide us with a single Pareto point. How will be go about finding other Pareto points? By altering the weights and solving again.
- 32. Multi-Objective Optimization As mentioned, such schemes are very common in multi-objective optimization. In fact, in an ASME paper published in 1997, Dennis and Das made the claim that all common methods of generating Pareto points involved repeated conversion of a multi-objective problem into a single objective problem and solving.
- 33. Multi-Objective Optimization Ok, so I march up and down my weights generating Pareto points and then I’ve got a good representation of my set. Unfortunately not. As it turns out it is seldom this easy. There are a number of pitfalls associated with using weighted sums to generate Pareto points.
- 34. Multi-Objective Optimization Some of those pitfalls are: Inability to generate points in non-convex portions of the frontier Inability to generate a uniform sampling of the frontier A non-intuitive relationship between combinatorial parameters (weights, etc.) and performances Poor efficiency (can require an excessive number of function evaluations).
- 35. Multi-Objective Optimization Let’s consider the 1st pitfall: What is a non-convex portion of the frontier? I assume you are all familiar with the concept of convexity so let’s move on to a pictorial.
- 36. Multi-Objective Optimization F2 Minimize Both F’s This is a non-convex region of the frontier F1
- 37. Multi-Objective Optimization Ok so why do weighted sum approaches have difficulty finding these points? As discussed in reference 1, choosing the weights in the manner that we have can be shown to be equivalent to rotating the performance axes by an angle that can be determined from the weights and then translating those rotated axes until they hit the frontier. The effect of this on a convex frontier can be visualized as follows.
- 39. Multi-Objective Optimization So I think that you can see already what is going to happen when the frontier is not convex. Consider the following animation.
- 41. Multi-Objective Optimization So we missed all the points in the non-convex region. This also demonstrates one reason why we may not get a uniform sampling of the Pareto frontier. As it turns out, a uniform sampling is only possible in this way for a Pareto set having a very specific shape. So not even all convex Pareto sets can be sampled uniformly in this fashion. You can read more about this in reference 1.
- 42. Multi-Objective Optimization Clearly, if we cannot generate a uniform sampling and we cannot find non-convex regions, then the relationship between changes in weights and motion along the frontier is non-intuitive. Finally, since with each combination of weights, we are completing an entire optimization of our system, You can see how this may result in a great deal of system evaluations.