#3 formal methods – propositional logic

Preparedby:SharifOmarSalem–ssalemg@gmail.com
Prepared by: Sharif Omar Salem – ssalemg@gmail.com
0

Prepositional logic is a formal system of representing
knowledge
Prepositional logic has:
 Syntax – what the allowable expressions are. Structure of the
sentence.
 Semantics – what the expressions mean. Meaning
 Proof theory – how conclusions are drawn from a set of
statements. Reasoning.
1

 Symbols represent facts
 E.g. “Penguins need a cold environment” is a fact
 That could be represented by the symbol P
 Each fact is called an atomic formulas or atoms
 Atomic propositions can be combined using logical connectives –
 Order of precedence: ￢ ∧ ∨ → ↔
2

These symbols P, Q,………. etc
used to represent propositions, are called
atomic formulas, or simply atoms.
To express more complex propositions such as the
following compound proposition, we use logical
connectives such as → (if-then or imply):
 “if car brake pedal is pressed, then car stops within five
seconds.”
This compound proposition is expressed in propositional
logic as:
 P → Q
3

 We can combine propositions and logical connectives to form
complicated formulas.
 Well-Formed Formulas: Well-formed formulas in propositional logic
are defined recursively as follows:
 1. An atom is a formula.
 2. If F is a formula, then (¬F) is a formula, where ¬ is the not operator.
 3. If F and G are formulas, then (F ∧ G), (F ∨ G), (F → G),and (F ↔G) are
formulas. (∧ is the and operator, ∨ is the or operator , ↔ stands for if and
only if or iff.)
 4. All formulas are generated using the above rules.
4

 Logic is made up sentences
 P might be a sentence
 P ∧ Q is also a sentence
 If we know the truth values of P and Q, we can work out the truth
value of the sentence.
 If P and Q are both true then P ∧ Q is true, otherwise it is false
 Can use truth tables to ascertain the truth of a sentence
5

 An interpretation of a propositional formula G is an assignment of
truth values to the atoms A1,... , An in G in which every Ai is
assigned either T or F, but not both.
 The Figure shows the truth table for several simple formulas.
6

 A literal is an atomic formula or the negation of an atomic formula.
 A clause is a wff express a fact (premises or conclusion).
 A clause set is a group of clause express an argument.
 A formula is in conjunctive normal form (CNF) if it is a conjunction
of disjunction of literals.
 A formula is in disjunctive normal form (DNF) if it is a disjunction of
conjunction of literals.
7

P - represents the fact “Penguins eat fish”
Q - represents the fact “Penguins like fish”
 P ∧ Q – Penguins eat fish and penguins like fish
 P ∨ Q – Penguins eat fish or penguins like fish
 ￢ Q – Penguins do not like fish
 P → Q
 Penguins eat fish therefore penguins like fish.
 If penguins eat fish then penguins like fish.
 P ↔ Q
 Penguins eat fish therefore penguins like fish
and penguins like fish therefore penguins eat fish.
8

 If the train arrives late and there is no taxi at the station, then john is
late for this meeting. John is not late for his meeting. The train did
arrive late. Therefore, there were taxis at the station.
9

10

11

12

Definition of Argument:
 An argument is a sequence of statements in which the conjunctionof
theinitialstatements(calledthepremises/hypotheses) is said to imply the
final statement (called the conclusion).
 An argument can be presented symbolically as
(P1 Λ P2 Λ ... Λ Pn)  Q
where P1, P2, ..., Pn represent the hypotheses and Q represents the
conclusion.
 Deriving a logical conclusion by combining many propositions and
using formal logic: hence, determiningthetruthofarguments.
 This formula representing the whole argument as hypothesis and
conclusion is known as NATURAL DEDUCTION
13

 What is a valid argument?
 An argument is valid if Q (conclusion) logically follow from P1, P2, ...,
Pn (hypotheses)
 Informal answer: Whenever the truth of hypotheses leads to the
conclusion
 A formula is valid iff it is true under all its interpretations. (Called
Tautology)
 A formula is invalid iff it is not valid.
 A valid argument is intrinsically true, i.e.
(P1 Λ P2 Λ ... Λ Pn)  Q is a tautology.
 Note: We need to focus on the relationship of the conclusion to the
hypotheses and not just any knowledge we might have about the
conclusion Q.
14

 Example:
 P1: Neil Armstrong was the first human to step on the moon.
 P2 : Mars is a red planet
And the conclusion
 Q: No human has ever been to Mars.
 This wff P1 Λ P2  Q is not a tautology ( Not True)
 Truth of Hypothesis doesn’t lead to the conclusion. Mean the
argument is not valid.
15

 Example:
 P1: Tokyo is located in Japan.
 P2 : Japan is not located in Europe.
And the conclusion
 Q: Tokyo is not located in Europe
 This wff P1 Λ P2  Q is a tautology ( Always True)
Truth of Hypothesis leads to the conclusion. Mean the argument
is valid.
16

 Russia was a superior power, and either France was not
strong or Napoleon made an error. Napoleon did not make
an error, but if the army did not fail, then France was strong.
Hence the army failed and Russia was a superior power.
 Converting it to a propositional form using letters A, B, C and D
A: Russia was a superior power
B: France was strong B: France was not strong
C: Napoleon made an error C: Napoleon did not make an
error
D: The army failed D: The army did not fail
17

A: Russia was a superior power
B: France was strong B: France was not strong
C: Napoleon made an error C: Napoleon did not make an error
D: The army failed D: The army did not fail
 Combining, the statements using logic
(A Λ (B V C)) hypothesis
C hypothesis
(D  B) hypothesis
(D Λ A) conclusion
 Combining them, the propositional form is
(A Λ (B V C)) Λ C Λ (D  B)  (D Λ A)
18

Example:
Real Madrid is a superior power team, and either FC Barcelona is not
strong or Juardiola make an error. Juardiola does not make an error, but
if FC Barcelona wins the game, then FC Barcelona is strong. Hence FC
Barcelona loses the game and Real Madrid is a superior power team.
 Converting atomic prepositions to propositional symbols
Converting it to a propositional form using letters W, X, Y and Z
W: Real Madrid is a superior power team.
X: FC Barcelona is strong X: FC Barcelona is not strong
Y: Juardiola make an error Y: Juardiola do not make an error
Z: FC Barcelona loses the game Z: FC Barcelona wins the game
19

W: Real Madrid is a superior power team.
X: FC Barcelona is strong X: FC Barcelona is not strong
Y: Juardiola make an error Y: Juardiola do not make an error
Z: FC Barcelona loses the game Z: FC Barcelona wins the game
 Convert verbal argument to propositional logic (hypothesis, conclusion
and form)
(W Λ (X V Y)) hypothesis
Y hypothesis
(Z  X) hypothesis
(Z Λ W) conclusion
Argument form is
(W Λ (X V Y)) Λ Y Λ (Z  X)  (Z Λ W)
20

Example:
 If the program is efficient, it executes quickly. Either the program is
efficient, or it has a bug. However, the program does not execute
quickly. Therefore it has a bug.
 Converting Key statements to propositional symbols
E: The program is efficient.
Q: The program executes quickly Q: The program does not
execute quickly
B: The program has a bug
21

 Convert verbal argument to propositional logic (hypothesis,
conclusion and form)
E  Q hypothesis
E ˅ B hypothesis
Q’ hypothesis
B conclusion
Argument form is
(E  Q) ˄ (E ˅ B) ˄ Q’  B
22

If the room temperature is hot, then the air conditioner is on. If
the room temperature is cold, then the heater is on. If the
room temperature is neither hot nor cold, then the room
temperature is comfortable. Therefore, If neither the air
conditioner nor the heater is on, then the room temperature
is comfortable.
Translate the argument using propositional Logic.
23

How to prove Validity of an argument?
 Truth Table proof
 Equivalency Laws deduction proof
 Resolution Theorem proof
24

If the room temperature is hot, then the air conditioner is on. If the room
temperature is cold, then the heater is on. If the room temperature is
neither hot nor cold, then the room temperature is comfortable. Therefore,
If neither the air conditioner nor the heater is on, then the room
temperature is comfortable.
 Converting Key statements to propositional symbols
 H = the room temperature is hot
 C = the room temperature is cold
 M = the room temperature is comfortable
 A = the air conditioner is on
 G = the heater is on.
 Convert propositional logic (hypothesis/conclusion/form)
 Hypothesis1: F1= H  A
 Hypothesis2: F2= C  G
 Hypothesis3: F3= ¬(H ˅ C)  M
 Conclusion: F4= ¬(A ˅ G)  M
Truth Table proof
25

 Argument Formula:
 F1 ˄ F2 ˄ F3  F4
 (H  A) ˄ (C  G) ˄ [¬(H ˅ C)  M]  [¬(A ˅ G)  M]
Truth Table proof
26

 To prove this proposition with the truth-table technique. You have to
exhaustively checks every interpretation of the formula F4 to
determine if it evaluates to T. The truth table shows that every
interpretation of F4 evaluates to T, thus F4 is valid.
27

Definition of Proof Sequence:
 It is a sequence of wffs in which each wff is either a hypothesis or
the result of applying one of the formal system’s derivation rules to
earlier wffs in the sequence.
 Derivation rules for propositional logic are
 Equivalence Rules.
 Inference Rules.
 Deduction Method.
Equivalency Laws-
Deduction proof
28

 Tautological proposition
 a tautology is a statement that can never be false
 all of the lines of the truth table have the result "true"
 Contradictory proposition
 a contradiction is a statement that can never be true
 all of the lines of the truth table have the result "false"
 Logical equivalence of two propositions
 two statements are logically equivalent if they will be true in exactly the
same cases and false in exactly the same cases
 all of the lines of one column of the truth table have all of the same
truth values as the corresponding lines from another column of the
truth table
 it's indicated using  or ↔
29

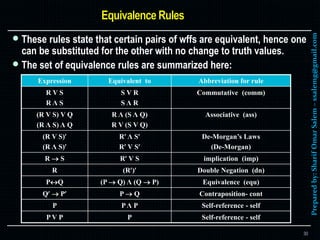
 These rules state that certain pairs of wffs are equivalent, hence one
can be substituted for the other with no change to truth values.
 The set of equivalence rules are summarized here:
30
Expression Equivalent to Abbreviation for rule
R V S
R Λ S
S V R
S Λ R
Commutative (comm)
(R V S) V Q
(R Λ S) Λ Q
R Λ (S Λ Q)
R V (S V Q)
Associative (ass)
(R V S)
(R Λ S)
R Λ S
R V S
De-Morgan’s Laws
(De-Morgan)
R  S R V S implication (imp)
R (R) Double Negation (dn)
PQ (P  Q) Λ (Q  P) Equivalence (equ)
Q  P P  Q Contraposition- cont
P PΛ P Self-reference - self
P V P P Self-reference - self

 Example for using Equivalence rule in a proof sequence:
 Simplify (A V B) V C to an argument.
The result must be an argument in the form of
P1 ^ P2^………..Pn  Q
31

 Example for using Equivalence rule in a proof sequence:
 Simplify (A V B) V C to an argument.
The result must be an argument in the form of
P1 ^ P2^………..Pn  Q
32

 Inference rules allow us to add a wff to the last part of the proof sequence,
if one or more wffs that match the first part already exist in the proof
sequence. ( Works in one direction , unlike equivalence rules)
33
From Can Derive Abbreviation for rule
R, R  S S Modus Ponens- mp
R  S, S R Modus Tollens- mt
R, S R Λ S Conjunction-con
R Λ S R, S Simplification- sim
R R V S Addition- add
P  Q, Q  R P  R Hypothetical syllogism- hs
P V Q, P Q Disjunctive syllogism- ds
(PΛ Q)  R P  (Q R) Exportation - exp
P, P Q Inconsistency - inc
PΛ (Q V R) (PΛ Q) V (PΛ R) Distributive - dist
P V (Q Λ R) (P V Q) Λ (P V R) Distributive - dist

 To prove an argument of the form
P1 Λ P2 Λ ... Λ Pn  R  Q
 Deduction method allows for the use of R as an
additional hypothesis and thus prove
P1 Λ P2 Λ ... Λ Pn Λ R  Q
34

Example :
 Prove (A  B) Λ (B  C)  (A  C)
35

 Prove that (P  Q)  (Q P) is a valid argument (called
Contraposition – con).
36

 Prove the argument
A Λ (B  C) Λ [(A Λ B)  (D V C)] Λ B  D
37

A Λ (B  C) Λ [(A Λ B)  (D V C)] Λ B  D
First, write down all the hypotheses.
1. A
2. B  C
3. (A Λ B)  (D V C)
4. B
38

A Λ (B  C) Λ [(A Λ B)  (D V C)] Λ B  D
First, write down all the hypotheses.
1. A
2. B  C
3. (A Λ B)  (D V C)
4. B
Use the inference and equivalence rules to get at the conclusion D.
5. C 2,4, mp
6. A Λ B 1,4, con
7. D V C 3,6, mp
8. C V D 7, comm
9. C  D 8, imp
and finally
10. D 5,9 imp
The idea is to keep focused on the result and sometimes it is very easy to go
down a longer path than necessary.
39

 Russia was a superior power, and either France was not strong or
Napoleon made an error. Napoleon did not make an error, but if the
army did not fail, then France was strong. Hence the army failed
and Russia was a superior power.
Q: Prove the upper argument ?
 From previous slides we translate this argument to the following
argument formula
 (A Λ (B V C)) Λ C Λ (D  B)  (D Λ A)
 Now we have to proof this propositional formula using proof
sequence.
40

Prove (A Λ (B V C)) Λ C Λ (D  B)  (D Λ A)
 Proof sequence
1. A Λ (B V C) hyp
2. C hyp
3. D  B hyp
4. A 1, sim
5. B V C 1, sim
6. C V B 5, comm
7. B 2, 6, ds
8. B  (D) 3, cont
9. (D) 7, 8, mp
10. D 9, dn
11. D Λ A 4, 10 , con
41

Example:
Real Madrid is a superior power team, and either FC Barcelona is not strong
or Juardiola make an error. Juardiola does not make an error, but if FC
Barcelona wins the game, then FC Barcelona is strong. Hence FC
Barcelona loses the game and Real Madrid is a superior power team.
argument formula
 (W Λ (X V Y)) Λ Y Λ (Z  X)  (Z Λ W)
 Now we have to proof this propositional formula using proof sequence.
42

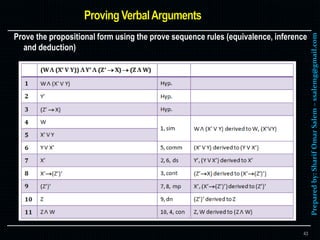
Prove the propositional form using the prove sequence rules (equivalence, inference
and deduction)
43

Example:
 If the program is efficient, it executes quickly. Either the program is
efficient, or it has a bug. However, the program does not execute
quickly. Therefore it has a bug.
argument formula
 (E  Q) ˄ (E ˅ B) ˄ Q’  B
 Now we have to proof this propositional formula using proof
sequence.
44

(E  Q) ˄ (E ˅ B) ˄ Q’  B
Prove the propositional form using the prove sequence
rules (equivalence, inference and deduction)
45

For Proving Verbal Arguments, you need to pass three steps
 Step 1: Converting atomic prepositions to propositional
symbols
 Step 2: Convert verbal argument to propositional logic
(hypothesis, conclusion and form)
 Step 3: Prove the propositional form using the prove sequence
rules (equivalence, inference and deduction)
46

47
End of Lecture

48

#3 formal methods – propositional logic

More Related Content

What's hot (20)

Similar to #3 formal methods – propositional logic (20)

More from Sharif Omar Salem (6)

Recently uploaded (20)

#3 formal methods – propositional logic