Lecture12_16717_Lecture1.ppt

CSE322
Finite Automata
Lecture #1

Terminologies
• Symbols:
– Symbols are an entity or individual objects, which can be any letter,
alphabet or any picture.
– Example: 1, a, b, #
• Alphabets:
– Alphabets are a finite set of symbols. It is denoted by ∑.
– Examples: ∑ = {a, b} , ∑ = {A, B, C, D} , ∑ = {0, 1, 2}, ∑ = {#, β, Δ}
• String:
• It is a finite collection of symbols from the alphabet. The string is
denoted by w.
• Example 1:
• If ∑ = {a, b}, various string that can be generated from ∑ are {ab,
aa, aaa, bb, bbb, ba, aba.....}.
• A string with zero occurrences of symbols is known as an empty
string. It is represented by ε.
• The number of symbols in a string w is called the length of a
string. It is denoted by |w|.

Definition
An automaton is defined as a system where energy, materials and
information are transformed, transmitted and used for
performing some functions without direct participation of man.

Definition
• An automaton is an abstract model of a digital computer.
• Every automaton includes some essential features.
• It has a mechanism for reading input.
– This input mechanism can read the input from left to right
– One symbol at a time
– Can also detect the end of the input string
• An automaton can produce output of some sort.
• It may have a temporary storage device.
• An automaton has a control unit which can be in any one of
finite number of internal states and which can change state in
some defined manner.

Finite Automaton
Input
“Accept”
or
“Reject”
String
Finite
Automaton
Output

Formal Definition
• Finite Automaton (FA)
 
F
q
Q
M ,
,
,
, 0



• Finite Automaton (FA)
 
F
q
Q
M ,
,
,
, 0



Q


0
q
F
: set of states
: input alphabet
: transition function
: initial state
: set of accepting states

DESCRIPTION: DETERMINISTIC FINITE AUTOMATON

Topics
 Acceptability of a String by a Finite Automaton
 Transition Graph and Properties of Transition Functions

• The transition function which maps
Q x ∑* into Q
(i.e. maps a state and a string of input symbols
including the empty string into a state) is called the
indirect transition function.

Transition Graph
initial
state
accepting
state
state
transition
0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,

0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
 
b
a,


b
a,
Input alphabet

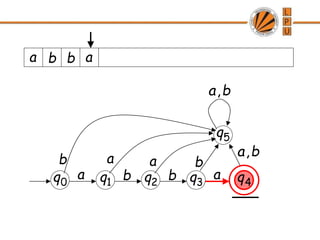
Initial Configuration
1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
Input String
a b b a
b
a,
0
q

Reading the Input
0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
a b b a
b
a,

0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
a b b a
b
a,

0
q 1
q 2
q 3
q 4
q
a b b a
accept
5
q
a a b
b
b
a,
a b b a
b
a,
Input finished

Rejection (other than abba)
1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
a b a
b
a,
0
q

0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
a b a
b
a,

0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
reject
a b a
b
a,
Input finished

Another Rejection on empty string
1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,
0
q


1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,
0
q
reject


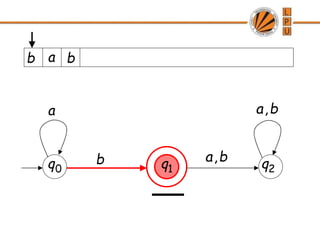
Another Example for accepting
a
b b
a,
b
a,
0
q 1
q 2
q
a b
a

a
b b
a,
b
a,
0
q 1
q 2
q
a b
a

a
b b
a,
b
a,
0
q 1
q 2
q
a b
a
accept
Input finished

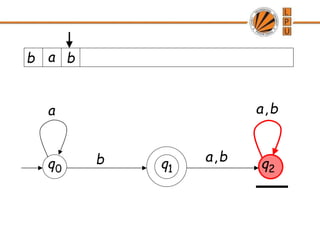
Rejection Example
a
b b
a,
b
a,
0
q 1
q 2
q
a
b b

a
b b
a,
b
a,
0
q 1
q 2
q
a
b b

a
b b
a,
b
a,
0
q 1
q 2
q
a
b b
reject
Input finished

Languages Accepted by FAs
FA
Definition:
The language contains
all input strings accepted by
= { strings that bring
to an accepting state}
M
 
M
L
M
M
 
M
L

0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,
   
abba
M
L  M
accept

Example ( being null string)
0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,
   
abba
ab
M
L ,
,

 M
accept
accept
accept

Example
a
b b
a,
b
a,
0
q 1
q 2
q
  }
0
:
{ 
 n
b
a
M
L n
accept trap state

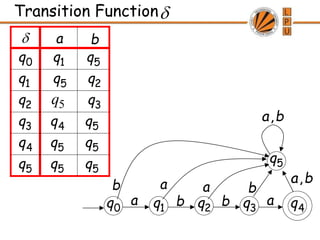
Transition Function 
0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
Q
Q 


:

b
a,

  1
0, q
a
q 

2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,
0
q 1
q

  5
0, q
b
q 

1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,
0
q

0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,
  3
2, q
b
q 


Transition Function
0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
 a b
0
q
1
q
2
q
3
q
4
q
5
q
1
q 5
q
5
q 2
q
5
q 3
q
4
q 5
q
b
a,
5
q
5
q
5
q
5
q

Extended Transition Function *

Q
Q 

 *
:
*

0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,

  2
0,
* q
ab
q 

3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,
0
q 1
q 2
q

  4
0,
* q
abba
q 

0
q 1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,

  5
0,
* q
abbbaa
q 

1
q 2
q 3
q 4
q
a b b a
5
q
a a b
b
b
a,
b
a,
0
q

Deterministic Final Automata
• DFA refers to deterministic finite automata.
– Deterministic refers to the uniqueness of the computation. The finite
automata are called deterministic finite automata if the machine reads
an input string one symbol at a time.
• In DFA, given the current state we know what the next step
will be.
• In DFA, there is only one path for specific input from the
current state to the next state.
• DFA does not accept the null move, i.e., the DFA cannot
change state without any input character.
• DFA accepts zero length string i.e. {}
• DFA can contain multiple final states. It is used in Lexical
Analysis in Compiler.

QUESTIONS
1. Draw a DFA which accept 00 and 11 at the end
of a string containing 0, 1 in it, e.g., 01010100
but not 000111010.
2. Construct a DFA which accepts set of all
strings over Σ={a,b} of length ≤2
3. Create a DFA which accepts strings of even
length.
4. Design a DFA in which start and end symbol
must be different
Given: Input alphabet, Σ={a, b}

QUESTIONS
5. Design a DFA in which every 'a' should be
followed by 'b'
Given: Input alphabet, Σ={a, b}
6. Design a DFA such that:
L = {anbm | n,m ≥ 1} Given: Input alphabet, Σ={a,
b}
Language L = {ab, aab, aaab, abbb, aabb,
aaaabbbb, ...}

Lecture12_16717_Lecture1.ppt

More Related Content

Similar to Lecture12_16717_Lecture1.ppt (20)

More from Venneladonthireddy1 (10)

Recently uploaded (20)

Lecture12_16717_Lecture1.ppt

Editor's Notes