Mergesort

Presentacion tomada del Depto. De Si stemas de la Universidad Nacional de Colombia se de Bogota Analysis of Algorithms

Merge-Sort INPUT: A sequence of numbers <a 1 ,a 2 ,a 3 ,...,a n > DIVIDE AND CONQUER PARADIGM Divide: the problem into a number of sub-problems Conquer: the sub-problems by solving them recursively Combine: the solutions to the sub-problems into the solution for the original problem

MERGE-SORT DIVIDE: Divide the n-element sequence to be sorted into two subsequences of n/2 elements each CONQUER: sort the two subsequences recursively using merge sort COMBINE: merge the two sorted subsequences to produce the sorted answer

STEPS: on a problem of size 1 do nothing on a problem of size at least 2 Split the sequence into two halves Sort one half of the numbers Sort the second half of the numbers Merge the two sorted lists MERGE-SORT

Given two lists to merge size n and m Maintain pointer to head of each list Move smaller element to output and advance pointer n m n+m ( First we study merge ) MERGE

auxiliary array smallest smallest A MERGE Keep track of smallest element in each sorted half. Insert smallest of two elements into auxiliary array. Repeat until done. This animation is taken form http://www.cs.princeton.edu/courses/cs226/lectures.html A G L O R H I M S T

auxiliary array smallest smallest MERGE A G A G L O R H I M S T

auxiliary array MERGE A G H smallest smallest A G L O R H I M S T

auxiliary array smallest MERGE A G H I smallest A G L O R H I M S T

auxiliary array smallest MERGE A G H I L smallest A G L O R H I M S T

auxiliary array smallest MERGE A G H I L M smallest A G L O R H I M S T

auxiliary array smallest MERGE A G H I L M O smallest A G L O R H I M S T

auxiliary array smallest MERGE A G H I L M O R smallest A G L O R H I M S T

auxiliary array smallest MERGE A G H I L M O R S first half exhausted A G L O R H I M S T

auxiliary array MERGE A G H I L M O R first half exhausted S T smallest A G L O R H I M S T

auxiliary array MERGE A G H I L M O R first half exhausted S T second half exhausted A G L O R H I M S T

MERGE ( A, p,q, r ) n 1  q-p+1 n 2  r-q create arrays L[1..n 1 +1] and R[1.. n 2 +1] for i  1 to n 1 do L[i]  A[p+i-1] for j  1 to n 2 do R[j]  A[q+j] L[n 1 +1]   R[n 2 +1]   i  1 j  1 for k  p to r do if L[i]  R[j] then A[k]  L[i] i  i+1 else A[k]  R[j] j  j+1 end_if end_for end. MERGE

... 2 7 MERGE ( A, 5,8,11 ) 9 A 5 1 7 9  k 2 6 4 7 8 ... 9 10 11 12 3 5 8 1 8 5 3  L R i j

... 2 7 9 A 5 7 9  2 6 4 7 8 ... 9 10 11 12 3 5 8 1 8 5 3  L R 1 k i j

... 3 9 A 5 7 9  2 6 4 7 8 ... 9 10 11 12 3 5 8 1 8 5 3  L R 1 2 k i j

... 5 A 5 7 9  2 6 4 7 8 ... 9 10 11 12 3 5 8 1 8 5 3  L R 1 2 3 k i j

... A 5 7 9  2 6 4 7 8 ... 9 10 11 12 7 5 8 1 8 5 3  L R 1 2 3 5 k i j

... A 5 7 9  2 6 4 7 8 ... 9 10 11 12 8 8 1 8 5 3  L R 1 2 3 5 7 k i j

... A 5 7 9  2 6 4 7 8 ... 9 10 11 12 8 1 8 5 3  L R 1 2 3 5 7 8 k i j

... A 5 7 9  2 6 4 7 8 ... 9 10 11 12 1 8 5 3  L R 1 2 3 5 7 8 9 k i j

MERGE- Correctness Loop Invariant At the start of each iteration of the for loop for k, the sub-array A[p,..,k-1] consist of the k-p smallest elements of L[1,.., n 1 +1] and R[1,.., n 2 +1] in sorted order. Moreover L[i] and R[j] are the smallest of their arrays that have not been copied back into A.

Before the beginning of the loop k=p, then the sub-array A[p,..,k-1] is empty and consist of the k-p = 0 smallest elements of L[1,.., n 1 +1] and R[1,.., n 2 +1]. Since i=j=1 then L[1] and R[1] are the smallest of their arrays that have not been copied back into A. INITILIZATION

MAINTENANCE Before the beginning of the l-th iteration of the loop k=p+l, then the sub-array A[p,..,k-1] consist of the (k-p = l) smallest elements of L[1,.., n 1 +1] and R[1,..,n 2 +1] in sorted order and L[i] and R[j] are the smallest elements of their arrays that have not been copied back into A.

Let us first assume that L[i]  R[j] then following the loop L[i] is copied to A[k =p+l] therefore before the beginning of the (l+1)th k=p+l+1 and A[p,..,k-1] = A[p,..,p+l] consist of the (l+1) smallest elements of L[1,.., n 1 +1] and R[1,..,n 2 +1] and L[i] and R[j] are the smallest elements of their arrays that have not been copied back into A.

Now suppose that R[j] < L[i] then following the loop R[j] is copied to A[k =p+l] therefore before the beginning of the (l+1)th k=p+l+1 and A[p,..,k-1] = A[p,..,p+l] consist of the (l+1) smallest elements of L[1,..,n 1 +1] and R[1,..,n 2 +1] and L[i] and R[j] are the smallest elements of their arrays that have not been copied back into A.

At termination k=r+1, then the sub-array A[p,..,k-1]= A[p,..,r] consist of the r smallest elements of L[1,..,n 1 +1] and R[1,..,n 2 +1] in sorted order. Since i= n 1 +1 and j= n 2 +1 then L[i] and R[j] are  . TERMINATION

MERGE-SORT MERGE(A, p, r): procedure that takes time  (n), where n=r-p+1 To sort call MERGE(A, 1, length[A]) with A = [ a 1 ,a 2 ,a 3 ,...,a n ] procedure MERGE-SORT( A, p, r ) if p<r then q   (p+r)/2  MERGE-SORT( A, p, q ) MERGE-SORT( A, q+1, r ) MERGE ( A, p, q, r )

Initial Sequence Sorted Sequence divide divide divide merge merge merge 5 2 4 6 1 3 2 6 5 2 4 6 1 3 2 6 5 2 4 6 5 2 2 5 4 6 4 6 2 4 5 6 1 3 2 6 1 3 1 3 2 6 2 6 1 2 3 6 1 2 2 3 4 5 6 6

Time complexity Analyzing divide and conquer algorithms The time can often be described by recurrence equation of the form  (1), if n  c, T(n) = aT(n/b)+D(n)+C(n) if n>c With a,b and c be nonnegative constants. If the problem is the small enough, say n  c , then the solution takes constant time  (1). If not the problem is divided in a subproblems with (1/b) size of the original. The division takes time D(n) and the combinations of sub-solutions takes time C(n) .

Analyzing MERGE-SORT In this case a=2, b=2, c=1, D(n)=  (1) and C(n)=  (n) then  (1), if n  1 , T(n) = 2T(n/2)+  (1)+  (n) if n>1 c if n  1 , T(n) = 2T(n/2)+ cn if n>1

Initial Sequence Sorted Sequence merge merge merge 1 2 2 3 4 5 6 6 2 4 5 6 1 2 3 6 2 5 2 6 1 3 4 6 5 2 4 6 1 3 2 6

Proof by Picture of Recursion Tree T( n ) T( n /2) T( n /2) T( n /4) T( n /4) T( n /4) T( n /4) T(1) T(1) T(1) T(1) T(1) T(1) T(1) T(1) cn T( n / 2 i ) c2( n /2) c4( n /4) c2 i ( n / 2 i ) cn . . . . . . lg n+1 cn(1+ lg n)

Lets suppose n power of two n=2 k The construction of the recursion tree T( n ) cn T( n /2) T( n /2)

cn c(n/2) c(n/2) T( n /4) T( n /4) T( n /4) T( n /4)

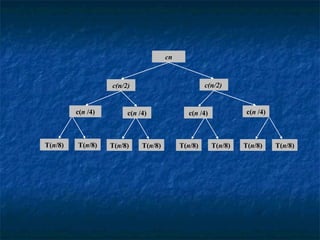
cn c(n/2) c(n/2) c( n /4) c( n /4) c( n /4) c( n /4) T( n /8) T( n /8) T( n /8) T( n /8) T( n /8) T( n /8) T( n /8) T( n /8)

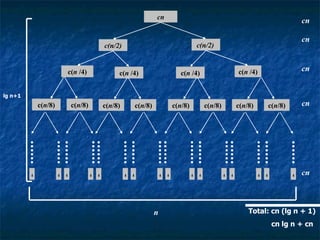
cn c(n/2) c(n/2) c( n /4) c( n /4) c( n /4) c( n /4) c( n /8) c( n /8) c( n /8) c( n /8) c( n /8) c( n /8) c( n /8) c( n /8) c c c c c c c c c c c c c c c c lg n+1 n Total: cn (lg n + 1) cn lg n + cn cn cn cn cn cn

k times Lets assume that n is power of two, i.e., n=2 k , k = lg n T(n) = 2T(n/2)+ cn = 2[2T(n/4)+ cn/2]+ cn = 4T(n/4)+ cn+ cn = 4[2T(n/8)+cn/4]+ cn+ cn= 8T(n/8)+cn+ cn+ cn . . = 2 k T(n/2 k )+cn+ . . . +cn . . = 2 k T(1)+k(cn) = cn+cn lg n Recursive substitution

In total including other operations let’s say each merge costs 3 per element output T(n)=T (  n/2  ) +T (  n/2  ) +3n for n  2 T(1)=1 Can use this to figure out T for any value of n T(5) =T(3)+T(2)+3x5 = (T(2)+T(1)+3x3)+(T(1)+T(1)+3x2)+15 = ((T(1)+T(1)+6)+1+9)+(1+1+6)+15 = 8+10+8+15 = 41 “ ceiling” round up “ floor” round down Exact recursive recurrence

Mergesort

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to Mergesort (20)

More from luzenith_g (20)

Recently uploaded (20)

Mergesort