08 numerical integration
Download as PPT, PDF•2 likes•2,373 views
This document discusses numerical integration techniques. It introduces the need for numerical integration when exact integrals cannot be calculated. The trapezoidal rule is derived using linear interpolation between points and applied to approximate integrals. Simpson's rule is then derived using quadratic interpolation and shown to be a more accurate method for numerical integration compared to the trapezoidal rule. Examples are provided to demonstrate applying these rules to calculate integrals numerically.
![ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
After substitutions and
manipulation!
( ) [ ]210 4
3
2
0
yyy
h
dxxf
x
x
++≈∫](https://image.slidesharecdn.com/08numericalintegration-101108031235-phpapp02/85/08-numerical-integration-16-320.jpg)
![ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
For 4-Intervals
( ) [ ]23210 424
3
4
0
yyyyy
h
dxxf
x
x
++++≈∫](https://image.slidesharecdn.com/08numericalintegration-101108031235-phpapp02/85/08-numerical-integration-17-320.jpg)
08 numerical integration
- 1. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Numerical Integration
- 2. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Objectives • The student should be able to – Understand the need for numerical integration – Derive the trapezoidal rule using linear interpolation – Apply the trapezoidal rule – Derive Simpson’s rule using parabolic interpolation – Apply Simpson’s rule
- 3. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Need for Numerical Integration! ( ) 6 11 01 2 1 3 1 23 1 1 0 231 0 2 =− ++= ++=++= ∫ x xx dxxxI ( ) 11 0 1 0 1 −−− −=−== ∫ eedxeI xx ∫ − = 1 0 2 dxeI x
- 4. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Interpolation! • If we have a function that needs to be integrated between two points • We may use an approximate form of the function to integrate! • Polynomials are always integrable • Why don’t we use a polynomial to approximate the function, then evaluate the integral
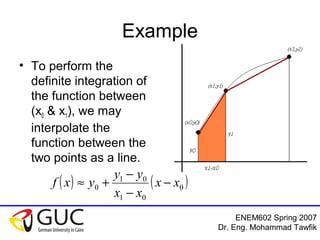
- 5. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Example • To perform the definite integration of the function between (x0 & x1), we may interpolate the function between the two points as a line. ( ) ( )0 01 01 0 xx xx yy yxf − − − +≈
- 6. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Example • Performing the integration on the approximate function: ( ) ( )∫∫ − − − +≈= 1 0 1 0 0 01 01 0 x x x x dxxx xx yy ydxxfI 1 0 0 2 01 01 0 2 x x xx x xx yy xyI − − − +≈
- 7. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Example • Performing the integration on the approximate function: − − − +− − − − +≈ 00 2 0 01 01 0010 2 1 01 01 10 22 xx x xx yy xyxx x xx yy xyI ( ) ( ) 2 01 01 yy xxI + −≈ • Which is equivalent to the area of the trapezium!
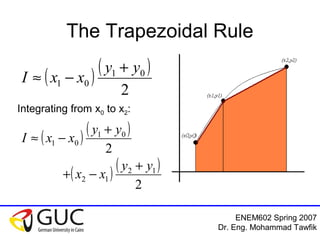
- 8. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik The Trapezoidal Rule ( ) ( ) 2 01 01 yy xxI + −≈ ( ) ( ) ( ) ( ) 2 2 12 12 01 01 yy xx yy xxI + −+ + −≈ Integrating from x0 to x2:
- 9. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik General Trapezoidal Rule • For all the points equally separated (xi+1-xi=h) • We may write the equation of the previous slide: ( ) ( ) ( ) ( ) ( )321 23 23 12 12 2 2 22 yyy h yy xx yy xxI ++= + −+ + −≈
- 10. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik In general ++≈ ∑ − = n n i i yyy h I 1 1 0 2 2 Where n is the number if intervals and h=total interval/n
- 11. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Example • Integrate • Using the trapezoidal rule • Use 2 points and compare with the result using 3 points ∫= 1 0 2 dxxI
- 12. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Solution • Using 2 points (n=1), h=(1-0)/(1)=1 • Substituting: ( )21 2 1 yyI +≈ ( ) 5.010 2 1 =+≈I
- 13. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Solution • Using 3 points (n=2), h=(1-0)/(2)=0.5 • Substituting: ( )321 2 2 5.0 yyyI ++≈ ( ) 375.0125.0*20 2 5.0 =++≈I
- 14. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Quadratic Interpolation • If we get to interpolate a quadratic equation between every neighboring 3 points, we may use Newton’s interpolation formula: ( ) ( ) ( )( )103021 xxxxbxxbbxf −−+−+≈ ( ) ( ) ( )( )1010 2 3021 xxxxxxbxxbbxf ++−+−+≈
- 15. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Integrating ( ) ( ) ( )( )1010 2 3021 xxxxxxbxxbbxf ++−+−+≈ ( ) ( ) ( )( )∫∫ ++−+−+≈ 2 0 2 0 1010 2 3021 x x x x dxxxxxxxbxxbbdxxf ( ) ( ) 2 0 2 0 10 2 10 3 30 2 21 232 x x x x xxx x xx x bxx x bxbdxxf ++−+ −+≈∫
- 16. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik After substitutions and manipulation! ( ) [ ]210 4 3 2 0 yyy h dxxf x x ++≈∫
- 17. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik For 4-Intervals ( ) [ ]23210 424 3 4 0 yyyyy h dxxf x x ++++≈∫
- 18. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik In General: Simpson’s Rule ( ) +++≈ ∑∑∫ − = − = n n i i n i i x x yyyy h dxxf n 2 ,..4,2 1 ,..3,1 0 24 30 NOTE: the number of intervals HAS TO BE even
- 19. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Example • Integrate • Using the Simpson rule • Use 3 points ∫= 1 0 2 dxxI
- 20. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Solution • Using 3 points (n=2), h=(1-0)/(2)=0.5 • Substituting: • Which is the exact solution! ( )210 4 3 5.0 yyyI ++≈ ( ) 3 1 125.0*40 3 5.0 =++≈I
- 21. ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Homework #7 • Chapter 21, pp. 610-612, numbers: 21.1, 21.3, 21.5, 21.25, 21.28. • Due date: Week 8-12 May 2005