10. Search Tree - Data Structures using C++ by Varsha Patil
- 1. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 1
- 2. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 2 Search trees are of great importance in an algorithm design It is always desirable to keep the search time of each node in the tree minimal
- 3. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 3 Variations in binary search trees: static and dynamic Ways of building trees of each type to guarantee that the trees remain balanced
- 4. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 4 BSTs are widely used for retrieving data from databases, look-up tables, and storage dictionaries It is the most efficient search technique having time complexity that is logarithmic in the size of the set
- 5. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 5 These two cases lead to the following two kinds of search trees: Static BST Dynamic BST
- 6. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 6 Static BST is the one that is not allowed to update its structure once it is constructed In other words, the static BST is an offline algorithm, which is presumably aware of the access sequence beforehand Static BST
- 7. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 7 A dynamic BST is the one that changes during the access sequence We assume that the dynamic BST is an online algorithm, which does not have prior information about the sequence Dynamic BST
- 8. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 8 While compilers and assemblers are scanning a program, each identifier must be examined to determine if it is a keyword This information concerning the keywords in a programming language is stored in a symbol table Symbol table is a kind of ‘keyed table’ The keyed table stores <key, information> pairs with no additional logical structure
- 9. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 9 The operations performed on symbol tables are the following: Insert the pairs <key, information> into the collection Remove the pairs <key, information> by specifying the key Search for a particular key Retrieve the information associated with a key
- 10. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 10 There are two different techniques for implementing a keyed table: symbol table and tree table Static Tree Tables Dynamic Tree Tables
- 11. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 11 Static Tree Tables When symbols are known in advance and no insertion and deletion is allowed, it is called a static tree table An example of this type of table is a reserved word table in a compiler
- 12. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 12 To optimize a table knowing what keys are in the table and what the probable distribution is of those that are not in the table, we build an optimal binary search tree (OBST) Optimal binary search tree is a binary search tree having an average search time of all keys optimal An OBST is a BST with the minimum cost
- 13. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 13 A dynamic tree table is used when symbols are not known in advance but are inserted as they come and deleted if not required Dynamic keyed tables are those that are built on-the- fly The keys have no history associated with their use
- 14. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 14 An AVL tree is a BST where the heights of the left and right subtrees of the root differ by utmost 1 and the left and right subtrees are again AVL trees The formal definition is as follows: An empty tree is height-balanced if T is a non- empty binary tree with TL and TR as its left and right subtrees, respectively
- 15. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 15 The balance factor of a node T, BF(T), in a binary tree is hL − hR, where hL and hR are the heights of the left and right subtrees of T, respectively For any node T in an AVL tree, the BF(T) is equal to −1, 0, or 1
- 16. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 16 For example, consider the BST as shown in Fig BF(Fri) = 0 BF(Mon) = +1 BF(Sun) = +2 Because BF(Sun) = +2, the tree is no longer height- balanced, and it should be restructured Unbalanced BST
- 17. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 17 In an AVL tree, after insertion of each node, it is checked whether the tree is balanced or not If unbalanced, it is rebalanced immediately A node is inserted or deleted from a balanced tree, then it may become unbalanced
- 18. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 18 So to rebalance it, the position of some nodes can be changed in proper sequence This can be achieved by performing rotations of nodes Rebalancing of AVL tree is performed using one of the four rotations: LL,RR,LR,RL
- 19. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 19 Balancing a tree by rotating towards right (a) Unbalanced Balanced tree
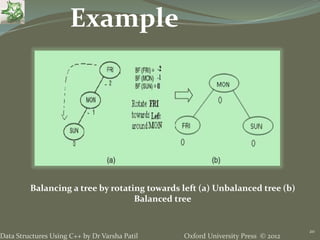
- 20. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 20 Balancing a tree by rotating towards left (a) Unbalanced tree (b) Balanced tree Example
- 21. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 21 Repetition Construct Case 1: LL (Left of Left) Consider the BST in Fig :
- 22. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 22 Case 2: RR (Right of Right)
- 23. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 23 Case 3: RL (Right of Left) Case LR for unbalanced tree due to insertion in right of left of a node (a)
- 24. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 24 Case 3: RL (Left to right) Case LR for unbalanced tree due to insertion in right of left of a node (a) Scenario 1 (b)
- 25. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 25 Case 3: RL (Right of Left) Case LR for unbalanced tree due to insertion in right of left of a node (a) Scenario 1 (b) Scenario 2 (c) Scenario 3
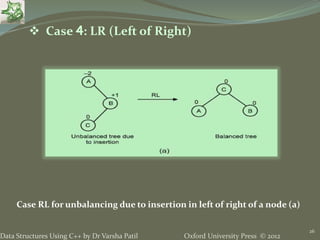
- 26. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 26 Case 4: LR (Left of Right) Case RL for unbalancing due to insertion in left of right of a node (a)
- 27. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 27 Case RL for unbalancing due to insertion in left of right of a node (a) Scenario 1 (b) Case 4: LR (Left of Right)
- 28. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 28 Case RL for unbalancing due to insertion in left of right of a node (a) Scenario 1 (b) Scenario 2 (c) Scenario 3 Case 4: LR (Left of Right)
- 29. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 29 Insertions and deletions in AVL tree are performed as in BSTs and followed by rotations to correct the imbalances in the outcome trees Unbalancing of an AVL tree due to insertion is removed in a single rotation However, imbalancing due to the deletion may require multiple steps for balancing
- 30. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 30 Figure demonstrates the deletion of a node in a given AVL tree (a) Original tree
- 31. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 31 (b) Delete 4
- 32. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 32 (c)Note the imbalance at node 3 implies an LL rotation around node 2
- 33. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 33 (d) Imbalance at node 5 implies a RR rotation around node 8
- 34. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 34 Search trees are of great importance in an algorithm design. It is always desirable to keep the search time of each node in the tree minimal. OBST maintains the average search time of all the nodes optimal. In an AVL tree, after insertion of each node, it is checked whether the tree is balanced or not. If unbalanced, it is rebalanced immediately. Rebalancing of AVL tree is performed using one of the four rotations: LL, RR, LR, RL. AVL trees work by insisting that all nodes of the left and right subtrees differ in height by utmost 1, which ensures that a tree cannot get too deep. Compilers use hash tables to keep track of the declared variables in a source code called as a symbol table. Imbalancing of an AVL tree due to insertion is removed in a single rotation. However, Imbalancing due to the deletion may require multiple steps for balancing.
- 35. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 35