![Table 9.1
Terminology Related to Asymmetric Encryption
Source: Glossary of Key Information Security Terms, NIST IR 7298 [KISS06]](https://image.slidesharecdn.com/12-public-keycryptographyandrsa-240721150458-23113bf7/85/12-Public-key-Cryptography-and-RSA-the-lecture-on-cryptography-2-320.jpg)
![Exponentiation in Modular
Arithmetic
• Both encryption and decryption in RSA involve
raising an integer to an integer power, mod n
• Can make use of a property of modular
arithmetic:
[(a mod n) x (b mod n)] mod n =(a x b) mod n
• With RSA you are dealing with potentially large
exponents so efficiency of exponentiation is a
consideration](https://image.slidesharecdn.com/12-public-keycryptographyandrsa-240721150458-23113bf7/85/12-Public-key-Cryptography-and-RSA-the-lecture-on-cryptography-21-320.jpg)
12- Public-key Cryptography and RSA the lecture on cryptography
- 1. Lecture 10 Dr Syed Muhammad Sajjad Department of Cyber-Security and Data Science Riphah Institute of Systems Engineering (RISE), Riphah International University, Islamabad, Pakistan. Cryptography Public-key Cryptography and RSA
- 2. Table 9.1 Terminology Related to Asymmetric Encryption Source: Glossary of Key Information Security Terms, NIST IR 7298 [KISS06]
- 3. Misconceptions Concerning Public‐Key Encryption • Public‐key encryption is more secure from cryptanalysis than symmetric encryption • Public‐key encryption is a general‐purpose technique that has made symmetric encryption obsolete • There is a feeling that key distribution is trivial when using public‐key encryption, compared to the cumbersome handshaking involved with key distribution centers for symmetric encryption
- 4. • The concept of public‐key cryptography evolved from an attempt to attack two of the most difficult problems associated with symmetric encryption: • Whitfield Diffie and Martin Hellman from Stanford University achieved a breakthrough in 1976 by coming up with a method that addressed both problems and was radically different from all previous approaches to cryptography Principles of Public‐Key Cryptosystems • How to have secure communications in general without having to trust a KDC with your key Key distribution Key distribution • How to verify that a message comes intact from the claimed sender Digital signatures Digital signatures
- 5. Public‐Key Cryptosystems • A public‐key encryption scheme has six ingredients: Plaintext The readable message or data that is fed into the algorithm as input Encryption algorithm Performs various transforma‐ tions on the plaintext Public key Used for encryption or decryption Private key Used for encryption or decryption Ciphertext The scrambled message produced as output Decryption algorithm Accepts the ciphertex t and the matching key and produces the original plaintext
- 7. Table 9.2 Conventional and Public‐Key Encryption
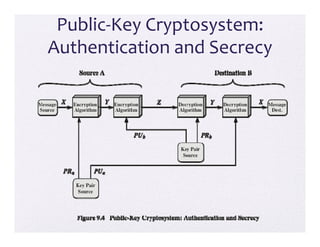
- 10. Public‐Key Cryptosystem: Authentication and Secrecy
- 11. Applications for Public‐Key Cryptosystems • Public‐key cryptosystems can be classified into three categories: • Some algorithms are suitable for all three applications, whereas others can be used only for one or two •The sender encrypts a message with the recipient’s public key Encryption/decryption Encryption/decryption •The sender “signs” a message with its private key Digital signature Digital signature •Two sides cooperate to exchange a session key Key exchange Key exchange
- 12. Table 9.3 Applications for Public‐Key Cryptosystems Table 9.3 Applications for Public-Key Cryptosystems
- 13. Public‐Key Requirements • Conditions that these algorithms must fulfill: • It is computationally easy for a party B to generate a pair (public‐key PUb, private key PRb) • It is computationally easy for a sender A, knowing the public key and the message to be encrypted, to generate the corresponding ciphertext • It is computationally easy for the receiver B to decrypt the resulting ciphertext using the private key to recover the original message • It is computationally infeasible for an adversary, knowing the public key, to determine the private key • It is computationally infeasible for an adversary, knowing the public key and a ciphertext, to recover the original message
- 14. Public‐Key Requirements • Need a trap‐door one‐way function • A one‐way function is one that maps a domain into a range such that every function value has a unique inverse, with the condition that the calculation of the function is easy, whereas the calculation of the inverse is infeasible • Y = f(X) easy • X = f–1(Y) infeasible • A trap‐door one‐way function is a family of invertible functions fk, such that • Y = fk(X) easy, if k and X are known • X = fk –1(Y) easy, if k and Y are known • X = fk –1(Y) infeasible, if Y known but k not known • A practical public‐key scheme depends on a suitable trap‐ door one‐way function
- 15. Rivest‐Shamir‐Adleman (RSA) Algorithm • Developed in 1977 at MIT by Ron Rivest, Adi Shamir & Len Adleman • Most widely used general‐purpose approach to public‐key encryption • Is a cipher in which the plaintext and ciphertext are integers between 0 and n – 1 for some n • A typical size for n is 1024 bits, or 309 decimal digits
- 16. RSA Algorithm • RSA makes use of an expression with exponentials • Plaintext is encrypted in blocks with each block having a binary value less than some number n • Encryption and decryption are of the following form, for some plaintext block M and ciphertext block C C = Me mod n M = Cd mod n = (Me)d mod n = Med mod n • Both sender and receiver must know the value of n • The sender knows the value of e, and only the receiver knows the value of d • This is a public‐key encryption algorithm with a public key of PU={e,n} and a private key of PR={d,n}
- 17. Algorithm Requirements • For this algorithm to be satisfactory for public‐ key encryption, the following requirements must be met: 1. It is possible to find values of e, d, n such that Med mod n = M for all M < n 2. It is relatively easy to calculate Me mod n and Cd mod n for all values of M < n 3. It is infeasible to determine d given e and n
- 19. Example of RSA Algorithm
- 21. Exponentiation in Modular Arithmetic • Both encryption and decryption in RSA involve raising an integer to an integer power, mod n • Can make use of a property of modular arithmetic: [(a mod n) x (b mod n)] mod n =(a x b) mod n • With RSA you are dealing with potentially large exponents so efficiency of exponentiation is a consideration
- 22. Summary • Public‐key cryptosystems • Applications for public‐ key cryptosystems • Requirements for public‐key cryptography • Public‐key cryptanalysis • The RSA algorithm • Description of the algorithm • Computational aspects