2. Linear Data Structure Using Arrays - Data Structures using C++ by Varsha Patil
- 1. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 1
- 2. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil To understand the well-defined, clear, and simple approach of program design To understand sequential organization of data To learn about arrays as sequential data organization; a valuable part of almost every programming language To understand the linear data structure and its implementation using sequential representation- Arrays To highlight the features of arrays To know about ordered list and its representation To use arrays efficiently for representing and manipulating polynomials, strings, and sparse matrices 2
- 3. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 3 Sequential organization allows storing data at a fixed distance apart. If the ith element is stored at location X, then the next sequential (i+1)th element is stored at location X+C, where C is constant.
- 4. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil If we intend to store a group of data together in a sequential manner in computer’s memory, then arrays can be one of the possible data structures. 4
- 5. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil An array is a finite ordered collection of homogeneous data elements which provides direct access (or random access) to any of its elements. An array as a data structure is defined as a set of pairs (index, value) such that with each index a value is associated. index — indicates the location of an element in an array. value - indicates the actual value of that data element. Declaration of an array in ‘C++’: int Array_A[20]; 5
- 6. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 6 Fig 2.1 Memory Representation A0 A1 . . . Ai . An-1 a i ai+1 ai+2 : : an-1 X(Base) X+1 X+2 X+(n-1) Array A
- 7. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 7 The address of the ith element is calculated by the following formula (Base address) + (offset of the ith element from base address) Here, base address is the address of the first element where array storage starts.
- 8. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil Generic Data type is a data type where the operations are defined but the types of the items being manipulated are not 8
- 9. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil Formally ADT is a collection of domain, operations, and axioms (or rules) For defining an array as an ADT, we have to define its very basic operations or functions that can be performed on it The basic operations of arrays are creation of an array, storing an element, accessing an element, and traversing the array 9
- 10. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 10 Let us specify ADT Array in which we provide specifications with operations to be performed. ADT ARRAY(Index, Value) declare CREATE( ) array ACCESS (array, index) value STORE (array, index, value) array for all Array_A ε array, x Î value, and i, j ε index let ACCESS (CREATE, i) = error. ACCESS (STORE (Array_A, i, x), j) = x if EQUAL (i, j) else ACCESS (Array_A, j) end end ARRAY.
- 11. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 11 Arrays support various operations such as traversal, sorting, searching, insertion, deletion, merging, block movement, etc. Insertion of an element into an array Deleting an element Memory Representation of Two-Dimensional Arrays Row-major Representation Column-major Representation
- 12. 12 Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil Columns Col1 col2 .... coln A11 A12 .... A1n A11 A12 .... A1n Am1 Am2 .... Amn : : : m*n Rows R1 R2 Rm 1 2 3 4 5 6 7 8 9 10 11 12 Matrix M =
- 13. 13 Row-major representation In row-major representation, the elements of Matrix are stored row-wise, i.e., elements of 1st row, 2nd row, 3rd row, and so on till mth row (0,0) (0,1) (0,2) (0,3) (1,0) (1,1) (1,2) (1,3) (2,0) (2,1) (2,2) (2,3) Row1 Row2 Row3 1 2 3 4 5 6 7 8 9 10 11 12 Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 14. 14 Row major arrangement Row 0 Row 1 Row m-1 Row 0 Row 1 Row m-1 Memory Location Row-major arrangement in memory , in row major representation Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 15. 15 The address of the element of the ith row and the jth column for matrix of size m x n can be calculated as: Addr(A[i][j]) = Base Address+ Offset = Base Address + (number of rows placed before ith row * size of row) * (Size of Element) + (number of elements placed before in jth element in ith row)* size of element As row indexing starts from 0, i indicate number of rows before the ith row here and similarly for j. For Element Size = 1 the address is Address of A[i][j]= Base + (i * n ) + j Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 16. 16 In general, Addr[i][j] = ((i–LB1) * (UB2 – LB2 + 1) * size) + ((j– LB2) * size) where number of rows placed before ith row = (i – LB1) where LB1 is the lower bound of the first dimension. Size of row = (number of elements in row) * (size of element)Memory Locations The number of elements in a row = (UB2 – LB2 + 1) where UB2 and LB2 are upper and lower bounds of the second dimension. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 17. 17 Column-major representation In column-major representation m × n elements of two- dimensional array A are stored as one single row of columns. The elements are stored in the memory as a sequence as first the elements of column 1, then elements of column 2 and so on till elements of column n Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 18. 18 Column-major arrangement col1 col2 Col n-1 Col 0 Col 1 Col 2 Memory Location … Column-major arrangement in memory , in column major representation Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 19. 19 The address of A[i][j] is computed as Addr(A[i][j]) = Base Address+ Offset= Base Address + (number of columns placed before jth column * size of column) * (Size of Element) + (number of elements placed before in ith element in ith row)* size of element For Element_Size = 1 the address is Address of A[i][j] for column major arrangement = Base + (j * m ) + I In general, for column-major arrangement; address of the element of the jth row and the jth column therefore is Addr (A[i][j] = ((j – LB2) * (UB1 – LB1 + 1) * size) + ((i –LB1) * size) Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 20. 20 Example 2.1: Consider an integer array, int A[3][4] in C++. If the base address is 1050, find the address of the element A[2] [3] with row-major and column-major representation of the array. For C++, lower bound of index is 0 and we have m=3, n=4, and Base= 1050. Let us compute address of element A [2][3] using the address computation formula 1. Row-Major Representation: Address of A [2][3] = Base + (i * n ) + j = 1050 + (2 * 4) + 3 = 1061 Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 21. 21 (0,0) (0,1) (0,2) (0,3) (1,0) (1,1) (1,2) (1,3) (2,0) (2,1) (2,2) (2,3) Row1 Row2 Row3 1 2 3 4 5 6 7 8 9 10 11 12 Row-Major Representation of 2-D array Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 22. 22 2. Column-Major Representation: Address of A [2][3] = Base + (j * m ) + i = 1050 + (3 * 3) + 2 = 1050 + 11 = 1061 Here the address of the element is same because it is the last member of last row and last column. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 23. 23 (0,0) (1,0) (2,0) (0,1) (1,1) (2,1) (0,2) (1,2) (2,2) (0,3) (1,3) (2,3) Col 1 Col 2 Col 3 Col 4 1 2 3 4 5 6 7 8 9 10 11 12 Column-Major Representation of 2-D array Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 24. 24 N -dimensional Arrays Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 25. 25 Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 26. 26 Row-Major representation of 2D array Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 27. 27 Three dimensions row-major arrangement (i*m2*m3) elements A[0][m2][m3] A[1][m2][m3] A[i][m2][m3] A[m1-1][m2] Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 28. 28 The address of A[i][j][k] is computed as Addr of A[i][j][k] = X + i * m2 * m3 + j * m3 + k By generalizing this we get the address of A[i1][i2][i3] … [ in] in n- dimensional array A[m1][m2][m3]. ….[ mn ] Consider the address of A [0][0][0]…..[0] is X then the address of A [i][0][0]….[0] = X + (i1 * m2 * m3 * - - -- - * mn ) and Address of A [i1][i2] …. [0] = X + (i1 * m2 * m3 * - -- - *mn ) + (i2 * m3 * m4 *--- * mn) Continuing in a similar way, address of A[i1][i2][i3]- - - -[ in] will be Address of A[i1][i2][i3]----[ in] = X + (i1 * m2 * m3 * - - -- - * mn) + (i2 * m3 * m4 *--- - - * mn )+(i3 * m4 * m5--- * mn + (i4 * m5 * m6-- - - - * mn +…….+ in = Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 29. 29 ARRAYS USING TEMPLATE The function is defined in similar way replacing int by T as datatype of member of array In all member functions header, Array is replaced by Array <T> :: now Following statements instantiate the template class Array to int and float respectively. So P is array of ints and Q in array of floats. Array <int> P; Array <float> Q; In similar we can also have array of any user defined data type Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 30. 30 CONCEPT OF ORDERED LIST Ordered list is the most common and frequently used data object Linear elements of an ordered list are related with each other in a particular order or sequence Following are some examples of the ordered list. 1, 3,5,7,9,11,13,15 January, February, March, April, May, June, July, August, September, October, November, December Red, Blue, Green, Black, Yellow Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 31. 31 There are many basic operations that can be performed on the ordered list as follows: Finding the length of the list Traverse the list from left to right or from right to left Access the ith element in the list Update (Overwrite) the value of the ith position Insert an element at the ith location Delete an element at the ith position Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 32. 32 SINGLE VARIABLE POLYNOMIAL Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 33. 33 Single Variable Polynomial Representation Using Arrays Array of Structures Polynomial Evaluation Polynomial Addition Multiplication of Two Polynomials Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 34. 34 Polynomial as an ADT, the basic operations are as follows: Creation of a polynomial Addition of two polynomials Subtraction of two polynomials Multiplication of two polynomials Polynomial evaluation Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
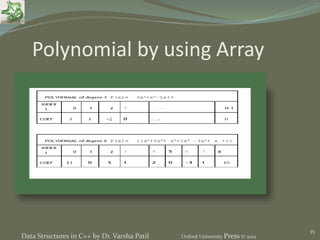
- 35. 35 Polynomial by using Array Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 36. 36 Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012 Polynomial by using Array
- 37. 37 Structure is better than array for Polynomial: Such representation by an array is both time and space efficient when polynomial is not a sparse one such as polynomial P(x) of degree 3 where P(x)= 3x3+x2–2x+5. But when polynomial is sparse such as in worst case a polynomial as A(x)= x99 + 78 for degree of n =100, then only two locations out of 101 would be used. In such cases it is better to store polynomial as pairs of coefficient and exponent. We may go for two different arrays for each or a structure having two members as two arrays for each of coeff. and Exp or an array of structure that consists of two data members coefficient and exponent. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 38. 38 Polynomial by using structure Let us go for structure having two data members coefficient and exponent and its array. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 39. 39 AN ARRAY FOR FREQUENCY COUNT We can use array to store the number of times a particular element occurs in any sequence. Such occurrence of particular element is known as frequency count. void Frequency_Count ( int Freq[10 ], int A [ 100]) { int i; for ( i=0;i<10;i++) Freq[i]=0; for ( i=0;i<100;i++) Freq[A[i] ++; } Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 40. 40 Frequency count of numbers ranging between 0 to 9 Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 41. 41 SPARSE MATRIX In many situations, matrix size is very large but out of it, most of the elements are zeros (not necessarily always zeros). And only a small fraction of the matrix is actually used. A matrix of such type is called a sparse matrix, Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 42. 42 Sparse Logical Matrix Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 43. 43 Sparse matrix and its representation Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 44. 44 Transpose Of Sparse Matrix Simple Transpose Fast Transpose Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 45. 45 Time complexity of manual technique is O (mn). Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 46. 46 Sparse matrix transpose Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 47. 47 Time complexity will be O (n . T) = O (n . mn) = O (mn2) which is worst than the conventional transpose with time complexity O (mn) Simple Sparse matrix transpose Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 48. 48 Fast Sparse matrix transpose In worst case, i.e. T= m × n (non-zero elements) the magnitude becomes O (n +mn) = O (mn) which is the same as 2-D transpose However the constant factor associated with fast transpose is quite high When T is sufficiently small, compared to its maximum of m . n, fast transpose will work faster Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 49. 49 It is usually formed from the character set of the programming language The value n is the length of the character string S where n ³ 0 If n = 0 then S is called a null string or empty string String Manipulation Using Array Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 50. 50 Basically a string is stored as a sequence of characters in one- dimensional character array say A. char A[10] ="STRING" ; Each string is terminated by a special character that is null character ‘0’. This null character indicates the end or termination of each string. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 51. 51 There are various operations that can be performed on the string: To find the length of a string To concatenate two strings To copy a string To reverse a string String compare Palindrome check To recognize a sub string. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 52. 52 Characteristics of array An array is a finite ordered collection of homogeneous data elements. In array, successive elements of list are stored at a fixed distance apart. Array is defined as set of pairs-( index and value). Array allows random access to any element In array, insertion and deletion of elements in between positions requires data movement. Array provides static allocation, which means space allocation done once during compile time, can not be changed run time. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 53. 53 Advantage of Array Data Structure Arrays permit efficient random access in constant time 0(1). Arrays are most appropriate for storing a fixed amount of data and also for high frequency of data retrievals as data can be accessed directly. Wherever there is a direct mapping between the elements and there positions, arrays are the most suitable data structures. Ordered lists such as polynomials are most efficiently handled using arrays. Arrays are useful to form the basis for several more complex data structures, such as heaps, and hash tables and can be used to represent strings, stacks and queues. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 54. 54 Disadvantage of Array Data Structure Arrays provide static memory management. Hence during execution the size can neither be grown nor shrunk. Array is inefficient when often data is to inserted or deleted as inserting and deleting an element in array needs a lot of data movement. Hence array is inefficient for the applications, which very often need insert and delete operations in between. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 55. 55 Applications of Arrays Although useful in their own right, arrays also form the basis for several more complex data structures, such as heaps, hash tables and can be used to represent strings, stacks and queues. All these applications benefit from the compactness and direct access benefits of arrays. Two-dimensional data when represented as Matrix and matrix operations. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012
- 56. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 56




![Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil
An array is a finite ordered collection of homogeneous data
elements which provides direct access (or random access) to
any of its elements.
An array as a data structure is defined as a set of pairs (index,
value) such that with each index a value is associated.
index — indicates the location of an element in an array.
value - indicates the actual value of that data element.
Declaration of an array in ‘C++’:
int Array_A[20];
5](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/85/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-5-320.jpg)









![15
The address of the element of the ith row and the jth column for matrix
of size m x n can be calculated as:
Addr(A[i][j]) = Base Address+ Offset = Base Address + (number
of rows placed before ith row * size of row) * (Size of Element) +
(number of elements placed before in jth element in ith row)*
size of element
As row indexing starts from 0, i indicate number of rows before the
ith row here and similarly for j.
For Element Size = 1 the address is
Address of A[i][j]= Base + (i * n ) + j
Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/85/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-15-320.jpg)
![16
In general,
Addr[i][j] = ((i–LB1) * (UB2 – LB2 + 1) * size) + ((j– LB2) * size)
where number of rows placed before ith row = (i – LB1)
where LB1 is the lower bound of the first dimension.
Size of row = (number of elements in row) * (size of
element)Memory Locations
The number of elements in a row = (UB2 – LB2 + 1)
where UB2 and LB2 are upper and lower bounds of the
second dimension.
Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/85/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-16-320.jpg)


![19
The address of A[i][j] is computed as
Addr(A[i][j]) = Base Address+ Offset= Base Address + (number of
columns placed before jth column * size of column) * (Size of
Element) + (number of elements placed before in ith element in ith
row)* size of element
For Element_Size = 1 the address is
Address of A[i][j] for column major arrangement = Base + (j *
m ) + I
In general, for column-major arrangement; address of the
element of the jth row and the jth column therefore is
Addr (A[i][j] = ((j – LB2) * (UB1 – LB1 + 1) * size) + ((i –LB1) * size)
Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/85/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-19-320.jpg)
![20
Example 2.1: Consider an integer array, int A[3][4] in C++. If
the base address is 1050, find the address of the element A[2]
[3] with row-major and column-major representation of the
array.
For C++, lower bound of index is 0 and we have m=3, n=4,
and Base= 1050. Let us compute address of element A [2][3]
using the address computation formula
1. Row-Major Representation:
Address of A [2][3] = Base + (i * n ) + j
= 1050 + (2 * 4) + 3
= 1061
Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/85/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-20-320.jpg)

![22
2. Column-Major Representation:
Address of A [2][3] = Base + (j * m ) + i
= 1050 + (3 * 3) + 2
= 1050 + 11
= 1061
Here the address of the element is same because it is the
last member of last row and last column.
Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/85/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-22-320.jpg)




![27
Three dimensions row-major arrangement
(i*m2*m3) elements
A[0][m2][m3] A[1][m2][m3] A[i][m2][m3] A[m1-1][m2]
Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/85/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-27-320.jpg)
![28
The address of A[i][j][k] is computed as
Addr of A[i][j][k] = X + i * m2 * m3 + j * m3 + k
By generalizing this we get the address of A[i1][i2][i3] … [ in] in n-
dimensional array A[m1][m2][m3]. ….[ mn ]
Consider the address of A [0][0][0]…..[0] is X then the address of A
[i][0][0]….[0] = X + (i1 * m2 * m3 * - - -- - * mn ) and
Address of A [i1][i2] …. [0] = X + (i1 * m2 * m3 * - -- - *mn ) + (i2 *
m3 * m4 *--- * mn)
Continuing in a similar way, address of A[i1][i2][i3]- - - -[ in] will be
Address of A[i1][i2][i3]----[ in] = X + (i1 * m2 * m3 * - - -- - * mn) +
(i2 * m3 * m4 *--- - - * mn )+(i3 * m4 * m5--- * mn + (i4 * m5 * m6--
- - - * mn +…….+ in =
Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/85/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-28-320.jpg)









![39
AN ARRAY FOR FREQUENCY COUNT
We can use array to store the number of times a particular
element occurs in any sequence. Such occurrence of
particular element is known as frequency count.
void Frequency_Count ( int Freq[10 ], int A [ 100])
{
int i;
for ( i=0;i<10;i++)
Freq[i]=0;
for ( i=0;i<100;i++)
Freq[A[i] ++;
}
Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/85/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-39-320.jpg)










![50
Basically a string is stored as a sequence of characters in one-
dimensional character array say A.
char A[10] ="STRING" ;
Each string is terminated by a special character that is null character
‘0’.
This null character indicates the end or termination of each string.
Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/85/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-50-320.jpg)





