48734407 cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser
- 1. CFD ANALYSIS OF FLUID FLOW THROUGH EQUIANGULAR ANNULAR DIFFUSER A major thesis submitted In partial fulfillment of the requirements for the award of the degree of Master of Engineering In Thermal Engineering By Mukesh Kumar Marothia Roll No. 3206 Under the Guidance of Prof. B. B. Arora Department of Mechanical Engineering, Delhi College of Engineering, University of Delhi Session 2003-05
- 2. Candidate’s Declaration I hereby declare that the work which is being present in the thesis entitled “ CFD Analysis of Fluid Flow Through Equiangular Annular Diffuser ” in partial fulfillment for the award of degree of Master of Engineering with specialization in “Thermal Engineering” submitted to Delhi College of Engineering, University of Delhi, is authentic record of my own work carried out under the supervision of Prof. B. B. Arora, Department of Mechanical Engineering, Delhi College of Engineering, University of Delhi. I have not submitted the matter in this dissertation for the award of any other Degree or Diploma or any other purpose whatever. (Mukesh Kumar Marothia) Univ. Roll No. – 3206 Date – July 27, 2005. College Roll No. – 16/ME(Th)/03 Certificate This is to certify that above statement made by the candidate is true to the best of my knowledge and belief. (B. B. Arora) Asstt. Professor Department of Mechanical Engg., Delhi College of Engg., Delhi.
- 3. Acknowledgement It is distinct pleasure to express my deep sense of gratitude and indebtedness to my learned supervisor Mr. B B. Arora, Asstt. Professor in the Department of Mechanical Engineering, Delhi College of Engineering, for his invaluable guidance, encouragement and patient review. His continuous inspiration only has made me complete this major dissertation. It is a great pleasure to have the opportunity to extent my heartiest felt gratitude to everybody who helped me throughout the course of this dissertation. I would also like to take this opportunity to present my sincere regards to my teachers for their kind support and encouragement. I am thankful to my friends and classmates for their unconditional support and motivation during this project. (Mukesh Kumar Marothia)
- 4. iii Abstract Diffuser is the important feature of turbomachinery, which is used for the efficient conversion of kinetic energy into pressure energy. Among the various types of diffusers, least attention has been given to annular diffusers because of the number of geometric parameters that needed to be considered. The geometric limitations in aircraft applications where the diffusers need to be specially designed so as to achieve maximum pressure recovery within the shortest possible length led to the development of annular diffusers. In the present study, the performance of a series of equiangular annular diffusers of various area ratio (2, 3, 4, and 5), lengths and divergence angle (10º, 15º, 20º and 25º) are determined with the help of FLOTRAN. The flow conditions at entrance are varied to evaluate how they affect the flow development in the passage. The value of Reynolds No at inlet is varied from 2.58×105 to 7.73×105. The result are present in the form of velocity diagram; pressure diagram; vector plot of velocity; static pressure distributaries and static pressure recovery coefficient along hub and casing wall; variation of Mach No at exit section of diffuser. The result indicates that pressure recovery increases with increases in area ratio. But pressure recovery is almost independent of Reynolds No. There was no separation on casing wall upto angle of 25º. The variation of Mach No is 0.15 to 0.46. In this range of Mach No, there is small change in pressure recovery upto cone angle of 15º. With further increases in angle, it reduces at somewhat higher rate.
- 5. iv Contents Certificate i Acknowledgement ii Abstract iii Contents iv List of figures vii List of tables ix Abbreviations x 1 Introduction 1-6 1.1 Type of Diffuser 1.1.1 Axial Diffusers 1.1.2 Radial Diffusers 1.1.3 Curved Wall Diffusers 1.2 Annular Diffusers 1.3 Performance parameters 1.3.1 Static Pressure Recovery Coefficient 1.3.2 Diffuser Effectiveness 1.3.3 Total Pressure loss coefficient 2 2 3 3 3 4 4 5 5 2 Literature Review 2.1 Effect of Geometric Parameters 2.1.1 Passage Divergence and Length 2.1.2 Wall Contouring 2.2 Effects of Flow Parameters 2.2.1 Aerodynamic Blockage 2.2.2 Inlet Swirl 2.2.3 Inlet Turbulence 2.2.4 Mach Number Influence 2.2.5 Reynolds Number Influence 2.3 Boundary Layer Parameter 7-15 9 9 11 12 12 12 13 14 14 14
- 6. v 2.3.1 Boundary Layer Suction 2.3.2 Blowing and Injection 15 15 3 CFD Analysis in FLOTRAN 3.1 FLOTRAN Features 3.2 FLOTRAN Capabilities 3.3 Getting Started Using FLOTRAN 3.3.1 FLOTRAN Processes 3.3.2 FLOTRAN Modeling 3.3.2.1 Modeling Constraints 3.3.2.2 Modeling Guidelines 3.3.2.3Boundary Condition Types 3.3.2.4 Optimum Order for Setting Boundary conditions 3.3.3 FLOTRAN Solution 3.3.3.1 Results Evaluation 3.3.4 FLOTRAN Post processing 3.3.4.1 Read Results File3.4 Error and Trouble Shooting 3.5 Errors and Trouble Shooting 3.5.1 Common Causes of Divergence 3.5.2 Trouble Shooting Guide 3.6 FLOTRAN Applications 16-26 18 18 19 19 19 20 20 20 20 21 21 22 22 24 24 25 25 4 FLOTRAN Mathematical Model 4.1 Fluid Flow Fundamentals 4.1.1. Continuity Equation 4.1.2. Momentum Equation 4.1.3. Compressible Energy Equation 4.1.4. Incompressible Energy Equation 4.1.5. Turbulence 4.1.5.1. Standard k-ε Model 4.1.5.2. RNG Turbulence Model 27-40 28 28 29 31 32 32 36 37
- 7. vi 4.1.5.3. NKE Turbulence Model 4.1.5.4. GIR Turbulence Model 4.1.5.5. SZL Turbulence Model 4.1.5.6. Standard k-ω Model 4.1.5.7. SST Turbulence Model 4.1.5.8. Near-Wall Treatment 4.1.6. Pressure 38 38 40 40 41 41 44 5 Results and Discussion 46-49 6 Conclusion and Future Scope 6.1 Conclusion 6.2 Future Scope 50-52 51 52 References Appendix 53-55 56-115
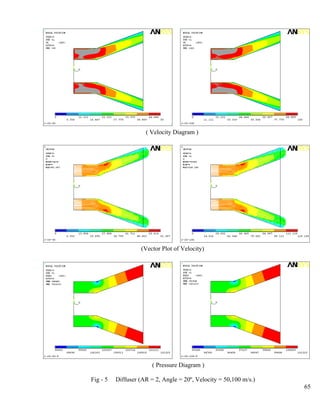
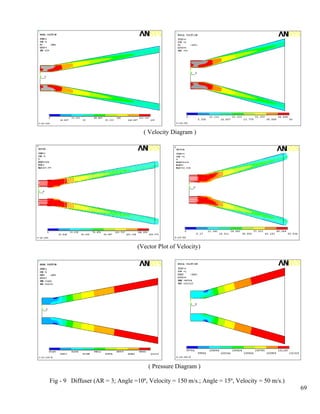
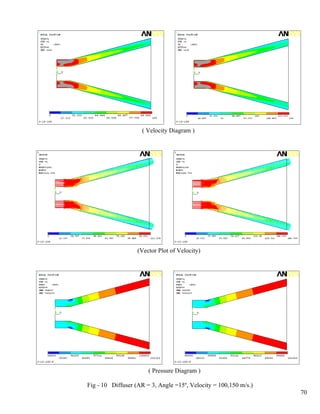
- 8. List of Figures 1 Annular Diffuser Performance Chart, B1≅.02, Sovaran and Klomp…………..………...61 Colour Figures of Pressure and Velocity 2 Diffuser (AR = 2, Angle =10º, Velocity = 50,100 m/s.)…………………………………62 3 Diffuser (AR = 2; Angle =10º, V = 150 m/s.; Angle = 15º, V = 50 m/s.)………………..63 4 Diffuser (AR = 2, Angle =15º, Velocity = 100,150 m/s.)………………………………..64 5 Diffuser (AR = 2, Angle = 20º, Velocity = 50,100 m/s.)………………………………...65 6 Diffuser (AR = 2; Angle = 20º, V = 150 m/s.; Angle = 25º, V = 50 m/s.)……………….66 7 Diffuser (AR = 2, Angle = 25º, Velocity = 100,150 m/s.)……………………………….67 8 Diffuser (AR = 3, Angle =10º, Velocity = 50,100 m/s.)………………………………... 68 9 Diffuser (AR = 3; Angle =10º, V= 150 m/s.; Angle = 15º, V= 50 m/s.)…………………69 10 Diffuser (AR = 3, Angle =15º, Velocity = 100,150 m/s.)………………………………..70 11 Diffuser (AR = 3, Angle =20º, Velocity = 50,100 m/s.)…………………………………71 12 Diffuser (AR = 3; Angle = 20º, V = 150 m/s.; Angle = 25º, V= 50 m/s.)………………..72 13 Diffuser (AR = 3, Angle =25º, Velocity = 100,150 m/s.)………………………………..73 14 Diffuser (AR = 4, Angle =10º, Velocity = 50,100 m/s.)…………………………………74 15 Diffuser (AR = 4; Angle =10º, V = 150 m/s.; Angle = 15º, V = 50 m/s.)………………..75 16 Diffuser (AR = 4, Angle =15º, Velocity = 100,150 m/s.)………………………………..76 17 Diffuser (AR = 4, Angle = 20º, Velocity = 50,100 m/s.)………………………………...77 18 Diffuser (AR = 4; Angle =20º, V = 150 m/s.; Angle = 25º, V = 50 m/s.)………………..78 19 Diffuser (AR = 4, Angle = 25º, Velocity = 100,150 m/s.)……………………………….79 20 Diffuser (AR = 5, Angle =15º, Velocity = 50,100 m/s.)…………………………………80 21 Diffuser (AR = 5; Angle =15º, V = 150 m/s.; Angle = 20º, V = 50 m/s.)………………..81 22 Diffuser (AR = 5, Angle = 20º, Velocity = 100,150 m/s.)……………………………….82 Static Pressure at Hub and Casing-wall 23 Static Pressure at Hub & Casing-wall (AR = 2, Angle = 10º)…………….……………..83 24 Static Pressure at Hub & Casing-wall (AR = 2, Angle = 15º)……………….…………..84 25 Static Pressure at Hub & Casing-wall (AR = 3, Angle = 10º)………………….………..85 26 Static Pressure at Hub & Casing-wall (AR = 3, Angle = 15º)…………………….……..86 27 Static Pressure at Hub & Casing-wall (AR = 3, Angle = 20º)…………………………...87 vii
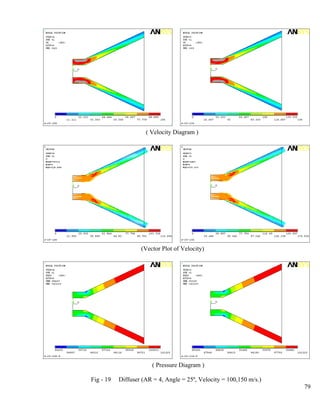
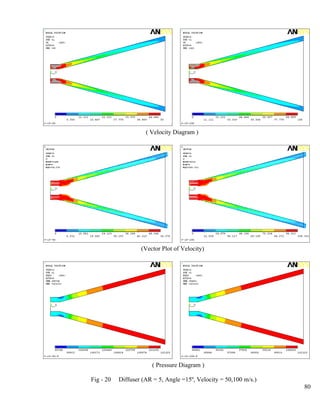
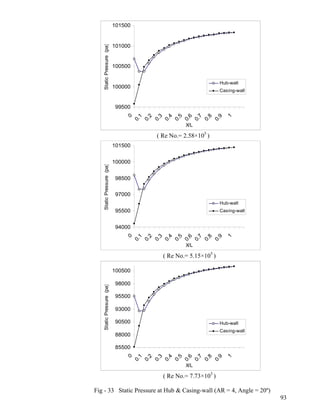
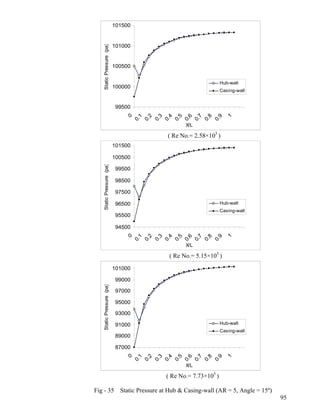
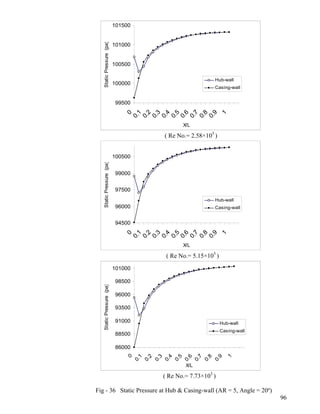
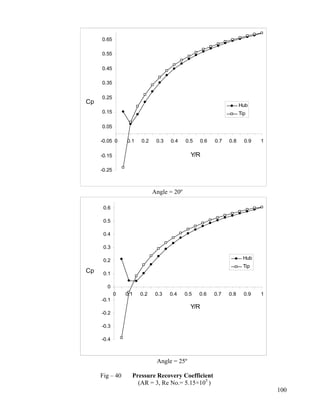
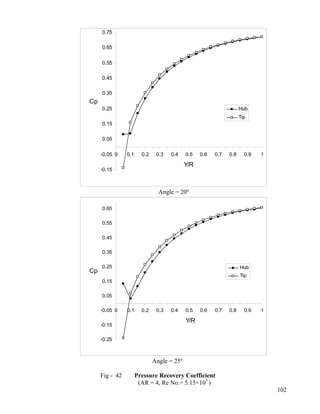
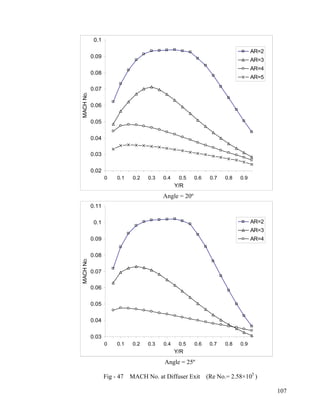
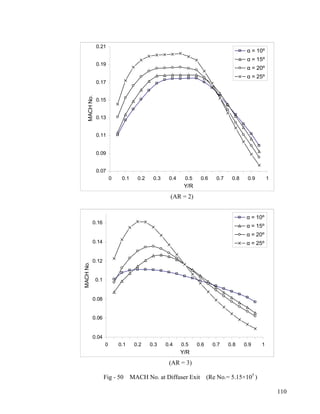
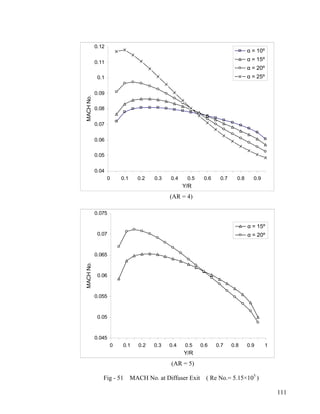
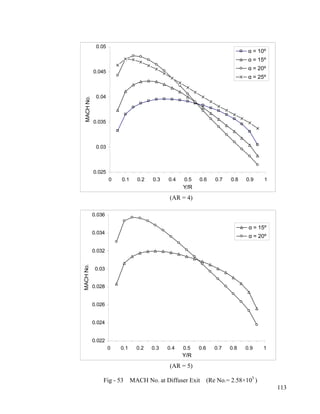
- 9. 28 Static Pressure at Hub & Casing-wall (AR = 3, Angle = 25º)…………………………...88 29 Static Pressure at Hub & Casing-wall (AR = 2, Angle = 20º)…………………………...89 30 Static Pressure at Hub & Casing-wall (AR = 2, Angle = 25º)…………………………...90 31 Static Pressure at Hub & Casing-wall (AR = 4, Angle = 10º)…………………………...91 32 Static Pressure at Hub & Casing-wall (AR = 4, Angle = 15º)…………………………...92 33 Static Pressure at Hub & Casing-wall (AR = 4, Angle = 20º)…………………………...93 34 Static Pressure at Hub & Casing-wall (AR = 4, Angle = 25º)…………………………...94 35 Static Pressure at Hub & Casing-wall (AR = 5, Angle = 15º)…………………………...95 36 Static Pressure at Hub & Casing-wall (AR = 5, Angle = 20º)…………………………...96 Pressure Recovery Coefficient at Hub and Casing-wall 37 AR = 2; Angle = 10º, 15º ; Re No.= 5.15×105...................................................................97 38 AR = 2; Angle = 20º, 25º ;Re No.= 5.15×105………………………...………………….98 39 AR = 3; Angle = 10º, 15º ;Re No.= 5.15×105………………… ……………………….99 40 AR = 3; Angle = 20º, 25º ;Re No.= 5.15×105………………… ………………...100 41 AR = 4; Angle = 10º, 15º ;Re No.= 5.15×105…………………… ……………...101 42 AR = 4; Angle = 20º, 25º ;Re No.= 5.15×105…………………… ………………...102 43 AR = 5; Angle = 15º, 20º ;Re No.= 5.15×105……………………… ………………...103 MACH No. at Diffuser Exit 44 Angle = 10º, 15º; Re No.= 5.15×105…………………………………………………..104 45 Angle = 20º, 25º; Re No.= 5.15×105…………………………………………………..105 46 Angle = 10º, 15º; Re No.= 2.58×105…………………………………………………..106 47 Angle = 20º, 25º; Re No.= 2.58×105…………………………………………………..107 48 Angle = 10º, 15º; Re No.= 7.73×105…………………………………………………..108 49 Angle = 20º, 25º; Re No.= 7.73×105…………………………………………………..109 50 AR = 2,3; Re No.= 5.15×105…………………………………………………………..110 51 AR = 4,5; Re No.= 5.15×105…………………………………………………………..111 52 AR = 2,3; Re No.= 2.58×105…………………………………………………………..112 53 AR = 4,5; Re No.= 2.58×105…………………………………………………………..113 54 AR = 2,3; Re No.= 7.73×105…………………………………………………………..114 55 AR = 2,3; Re No.= 7.73×105…………………………………………………………..115 viii
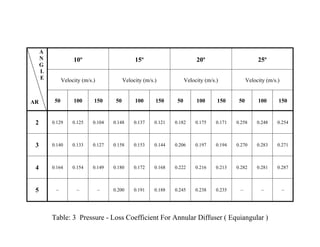
- 10. List of Tables 1 Table 1Geometric Parameters For Tested Annular Diffuser……………………..…57 2 Table 2 Static Pressure Recovery Coefficients for Annular Diffuser (Equiangular)...58 3 Table 3 Pressure Loss Coefficients for Annular Diffuser (Equiangular)…………….59 ix
- 11. Abbreviations A Area AR Area Ratio AS Aspect Ratio B Blockage b Dimension Cd Disc Arch Coefficient Cf Friction Coefficient Cp Static Pressure Recovery Coefficient Cp* Line of Maximum Cp for Minimum L/R Cp** Line of Maximum Cp for Minimum Ar Cpo Total Pressure Loss Coefficient Cpt Total Pressure Loss Coefficient Cpi Ideal Pressure Coefficient G Gravitational Acceleration H Passage Height, Shape Factor K Total Pressure Loss Coefficient M Mach Number L Length M Mass Flow, Momentum Ratio P Pressure Pt Total Pressure Pr Pressure Ratio P Static Pressure Q Volume Flow Rate Re Reynolds Number R Radius Tu Turbulence Intensity T Thickness U, V, W Velocity Components x
- 12. X, Y, Z Cartesian Coordinates Vx, Vy, Vz Components of the Velocity Vector in the x, y and z Directions ρ Density T Time R Gas Constant T Temperature Β Bulk Modulus Τij Stress Tensor Ui Orthogonal Velocities (U1 = Vx, U2 = Vy, U3 = Vz) Μ Dynamic Viscosity Λ Second Coefficient Of Viscosity Gx, Gy, Gz Components of Acceleration Due To Gravity Rx, Ry, Rz Distributed Resistances Tx, Ty, Tz Viscous Loss Terms Cp Specific Heat To Total (Or Stagnation) Temperature K Thermal Conductivity Wv Viscous Work Term Qv Volumetric Heat Source Φ Viscous Heat Generation Term Ek Kinetic Energy V Magnitude of the Fluid Velocity Vector xV Mean Component of Velocity In X-Direction Fluctuating Component of Velocity In X-Direction ΣrxVr Reynolds Stress Terms Μt Turbulent Viscosity Φ Viscous Dissipation Lx Length Scale Ln Shortest Distance from the Node to the Closest Wall Lc Characteristic Length Scale Cμ Turbulence Constant xi
- 13. k Turbulent kinetic energy ( ENKE ) ε Turbulent kinetic energy dissipation rate ( ENDS ) ω Specific dissipation rate Cr Constant depending on turbulence model used Ωm Angular velocity of the coordinate system εmji Alternating tensor operator vtan Velocity parallel to the wall τ Shear stress ν Kinematic viscosity κ Slope parameter of law of the wall E Law of the wall constant δ Distance from the wall εen Near wall dissipation rate knw Near wall kinetic energy ρo Reference density Pref Reference pressure {g} Acceleration vector due to gravity Pabs Absolute pressure Prel Relative pressure {r} Position vector of the fluid particle w. r. to rotating {ω} Constant angular velocity vector of the coordinate system {V} Vector velocity in the rotating coordinate system Pr Prandtl number μe Effective viscosity Ke Effective conductivity σt Turbulent Prandtl (Schmidt) Number xii
- 15. Introduction Chapter 1 A diffuser is a device that increases the pressure of a fluid at the expense of its kinetic energy. The cross-section area of diffuser increases in the direction of flow, therefore fluid is decelerated as it flows through it causing a rise in static pressure along the stream. Such a process is known as diffusion. The flow process near the diffuser walls is subjected to greater retardation due to the formation and development of the boundary layer. A study of the parameters governing the development of the boundary layer and their relationship with diffuser performance is, therefore vital in optimizing the design of a diffuser. Diffusers are extensively used in centrifugal compressors, axial flow compressors, ram jets, combustion chambers, inlet portions of jet engines etc. The energy transfer in these turbomachineries involves the exchange of significant levels of kinetic energy in order to accomplish the intended purpose. As a consequence, very large levels of residual kinetic energy frequently accompany the work input and work extraction processes, sometime as much as 50% of the total energy transferred. A small change in pressure recovery can increases the efficiency significantly. Therefore diffusers are absolutely essential for good turbomachinery performance. 1.1 TYPE OF DIFFUSERS 1.1.1 Axial Diffuser – In axial diffusers, fluid flows along the axis of diffusers and there is continuous retardation of the flow. Axial diffuser is divided in to the following categories- • Conical diffuser • Channel diffuser • Annular diffuser The basic geometric parameters for these type of diffusers are as follows: For conical diffuser- Nondimensional length, L/W1 Aspect ratio, AS = b/W1 Area ratio, AR = A2/A1 ()θtan211WLAR+= For channel diffuser- Nondimensional length, L/D1 Area ratio, AR = A2/A1 ()[]21tan21θDLAR+= 2
- 16. Introduction Chapter 1 For annular diffuser- Nondimensional length, L/Δr or L/h Area ratio, AR = A2/A1 ()θsin211hLAR+= (for equiangular case) 1.1.2 Radial Diffuser – In radial diffusers fluid flows in radially outward direction in confined space between the two boundaries. Diffuser used in radial turbo machinery fall under this category. They may be vane less and vaned types. unlike the axial diffuser, this type of diffuser may convert kinetic energy into static pressure rise by one or two principles – an increases in flow passage area in order to bring about a reduction in the average velocity; – a change in the mean flow path radius to bring about a recovery in angular velocity according to the conservation of angular momentum. 1.1.3 Curved Wall Diffuser – In recent time most of the aircrafts use curved wall diffuser. In aircraft engines several modifications may introduce nonuniformities and higher level of turbulence in flow field entering the diffuser. In addition mechanical and structural requirement place limits on the length of the passage. Curved wall diffuser is useful in this case and compatible with down stream requirement of flow besides it, these diffuser are also of fundamental and practical interest for various other applications like gas turbine system. Curved diffusers are broadly classified as – • 90 or part turn diffuser or half diffuser. • 180 or U- diffuser. • S- Diffuser. • Y-Diffuser. 1.2 ANNULAR DIFFUSER For decades researchers have paid more attention to conical diffuser and channel diffuser than to annular diffusers. But, the annular diffusers have a very strong industrial significance and have received attention in recent years. These types of diffuser are very much used in aircraft applications. With the help of annular diffuser the maximum presser recovery is achieved within the shortest possible length. With annular diffuser, good performance is possible with large wall angles since an inner surface is present to guide the flow radially outward. The annular diffuser affords the possibility of 3
- 17. Introduction Chapter 1 introducing many different geometric combinations since there is now an inner surface that can be varied independently of the outer surface. It is more difficult to define the essential geometric parameters for annular diffusers since the numbers of independent variables are large. The essential variables to define the geometry of annular diffuser are two wall angles, area ratio, nondimentional length and inlet radius ratio. As the number of variables increases, geometry becomes more complex. By suitable combination of these variables we can find out number of geometry. The present study investigates the equiangular type of annular diffuser. In these types of annular diffusers both hub and casing are diverging outward with same angle of divergence. The geometry for different equiangle of divergence of 10º, 15º, 20º and 25º and for different area ratios of 2, 3, 4 and 5 are presented in table 1. 1.3 PERFORMANCE PARAMETERS Performance parameters are very helpful in designing and predicting the performance of diffusers. These parameters reveal that diffuser geometry will give the desire output or not. The following parameters are important to find out diffuser performance. 1.3.1 Static Pressure Recovery Coefficient – The pressure recovery coefficient of a diffuser is most frequently defined as the static pressure rise through the diffuser divided by the inlet dynamic head. 121221avpvppC ρ − = where subscripts 1 and 2 refers to diffuser inlet and outlet conditions respectively. vav1 represents the average velocity at the inlet. An ideal pressure recovery can be defined if the flow is assumed to be isentropic. Then, by employing the conservation of mass, this relation can be converted to an area ratio for incompressible flow. 211ARCpi−= 4
- 18. Introduction Chapter 1 1.3.2 Diffuser Effectiveness – The diffuser effectiveness is simply the relation between the actual recovery and the ideal pressure recovery. pipCC/=η This is an excellent parameter for judging the probable level of performance when it is necessary to estimate the expected performance under unknown conditions, relative to available data. 1.3.3 Total Pressure Loss Coefficient – The total pressure loss coefficient reflects the efficiency of diffusion and drag of the system. The most common definition of loss coefficient is as the ratio of total pressure rise to the diffuser inlet dynamic head. 12020121avvppK ρ − = ppiCARCUuuK−−=−−=)/(/)(22122221αα where is the total pressure in the core region at the exit, the over bar indicate the mass averaged quantity, and oip1α and 2α are the kinetic energy parameters at the inlet and exit of the diffuser . For the case where the velocity profile at the inlet of diffuser is flat with a thin wall boundary layer, 11≈α. However, due to the thickening of boundary layer through the diffuser, 2αis generally greater than unity. Nonetheless, it is often assumed that kinetic energy coefficient are equal to unity, than ppiCCK−= Since flow in diffusers are subjected to an adverse pressure gradient there is a potential danger for flow separation to occur which could lead to loss in performance as well as damage of downstream equipment. The aim of design is to keep the adverse pressure gradient as high as possible, but below a critical limit, by controlling the length versus area-ratio of the diffuser. 5
- 19. Introduction Chapter 1 The design requirements for a good diffuser are as following- 1. Convey the flow efficiently transferring a portion of the kinetic energy into a static pressure rise. 2. It must accept a variety of inlet conditions including extreme swirl, blockage and Mach number. 3. Deliver the fluid with reasonable velocity and angle profiles without separated regions. 4. Wall curvature must not have a deleterious effect upon passage performance. 5. Pressure recovery achieved over a short axial length. While obtaining the best possible design, some limitations are imposed on a diffuser. 1. Limited length 2. Specified area ratio 3. Specified cross- sectional shape 4. Maximum static pressure recovery 5. Minimum stagnation pressure loss It is not hard to appreciate that the performance of the diffuser directly and often strongly influences the overall efficiency of the turbomachine. Thus the detailed processes which occur in diffusing elements must be carefully understood and thoroughly optimized if good turbomachinery performance is to be obtained. 6
- 20. Chapter 2 Literature Review
- 21. Literature Review Chapter2 Diffusers are one of the standard challenges in fluid mechanics. The task of a diffuser is to decelerate the flow and to regain total pressure. It is more difficult to arrange for an efficient deceleration of flow than it is to obtain an efficient acceleration. There is a natural tendency in a diffusing process for the flow to break away from the walls of the diverging passage, reverse its direction, and flow back in direction of the pressure gradient. If the divergence is too rapid, this may result in the formation of eddies with consequent transfer of some kinetic energy into internal energy and a reduction in useful pressure rise. A small angle of divergence, however, implies a long diffuser and a high value of skin friction loss. Usually, flow separation in a diffuser is sought to be avoided due to the invoked additional pressure loss. Other than in many strongly separated flows, such as the flow over a backward facing step, the point of flow separation, in diffuser, is not defined by the geometry but entirely by the pressure gradient. Hence, diffuser flows are very sensitive and are difficult to predict with numerical means. Diffusers have been studied extensively in the past, since this is a very common flow configuration. Apart from the characterization of diffusers, these flows are used to study fundamental physics of pressure-driven flow separations. Historically, annular diffusers have ranked after channel and conical diffusers in terms of interest for research and hence fewer works is available upon which to establish the technology base for design and performance evaluation. Although annular diffusers are used in gas turbines and turbomachinery installations, it is only in the last decade that there have been any systematic investigations of there performance characteristics. The most notable contribution is that due to Sovran and Klomp [27] who tested over one hundred different geometries, nearly all of which had conically diverging center bodies with an inlet radius ratio (Ri/Ro) of 0.55 to 0.70. The tests were carried out with a thin inlet boundary layer and the diffusers have free discharge. The tests were present as contours of pressure recovery plotted against area ratio and non-dimensional length. Howard et al [12] also tested symmetrical annular diffusers with center bodies of uniform diameter, using fully developed flow at inlet. The limits of the various flow regimes and the optimum performance lines were established. Besides it, some other researchers also contributed in the field of annular diffuser and concluded various important results. Much of the extent data covering the annular diffusers was done in the experimental laboratory to uncover some of the unusual performance characteristics of annular diffusers. But there are still some important unresolved questions. The reason for it is that the numbers of 8
- 22. Literature Review Chapter2 independent varibals are large for annular diffusers. In the annular diffuser the flow take place between two boundary surfaces which can varies independently. This chapter involves a systematic study of different geometric and flow parameters which influence the overall and internal performance of annular diffusers. In this regard the available literature has been examined with a view to make comments on the state of the art and to recognize the scope of further research on the subject. 2.1 Effect of Geometric Parameters In an annular diffuser, a number of different geometric variables can influence the variation of pressure recovery and inlet condition of flow. The basic equations of motion reveal the importance of both geometric and aerodynamic parameters on the ultimate performance of annular diffuser. The specification of a wide variety of geometric parameters is essential before the performance of diffuser is given. In this section, the various geometric parameters and there influence on diffuser performance is reviewed. 2.1.1 Passage Divergence and Length Area ratio and non-dimension length prescribes the overall diffusion and pressure– gradient respectively, which is the principle factor in boundary layer development. The study by Henry and Wood (1958) [36] is useful to understand the subsonic annular diffuser. Two diffusers with area ratio 2.1 and divergence of 5º and 10º were tested at various Mach number. It found by this study that most of data clusters around a line of constant effectiveness. It is also observed that the inner wall is being starved of fluid. If a higher divergence had been used, then one might anticipate stall on the inner surface. An extensive study is carried out by Kmonicek and Hibs (1974) [21] in which, the pressure loss coefficient is found out on the basis of the work of compression required to meet the static pressure rise, the results are very interesting but difficult to understand due to use of unconventional terminology. Sovran and Klomp (1967) [27] and Howard et al. (1967) [12] produced the first widely used annular diffuser maps for channel diffusers. Sovran and Klomp [27] conducted a large number of performance measurements which spanned a broad selection of geometric types of diffusers. The map is only a broad representation of the bulk of 9
- 23. Literature Review Chapter2 configurations tested in the vicinity of their best performance areas. The poorer diffusers are not well defined by the map. These maps also show optimal diffuser geometrics under different conditions and two optimum lines are established. The line of Cp* shows the best area ratio for a given length/passage height ratio, and the line of Cp** shows the best length/ passage height ratio for a given area ratio. The same results were find out by Howard et al [12]. The important difference between this and the Sovran and Klomp [27] map was that the latter was made for very low inlet aerodynamic blockage whereas the former study was carried out for fully developed inlet profiles, implying high aerodynamic blockage. Along the line of peak recovery there is fairly good agreement between the two maps but in the region of heavy transitory stall the maps disagree substantially. Johnston (1959) [19] and Johnston (1953) [18] reported a study of four different annular diffusers. Three of the four agree tolerably well with the basics Sovran and Klomp [27] map, one of them disagree substantially; the case a strong disagreement is probably in stall. Srinath (1968) [28] studied four equiangular annular diffuser with 2θ = 7º, 10º, 15º and 20º respectively. Tests were reported with a variety of L/Δr values. The line of best pressure recovery shown as CP* by Sovran and Klomp [27] was again confirmed, and Srinath’s map is quite similar to that of Howard et al. [12]. Srinath [28] also observed that the existence of a down stream pipe improved the pressure recovery of the diffuser itself. An extensive study of diffusers which, although annular, begin with a circular cross section was reported by Ishikawa and Nakamura (1989) [13]. The author found that the performance of the diffuser differed significantly depending on whether it is parallel or diverging for L/r1 greater than about 2. When both types have the same non dimensional length and area ratio, the parallel diffuser has the higher CP. The lines of optimum performance are also drawn. The line of CP* shows the best area ratio for a given non dimensional length, and the line of CP** shows the best non dimensional length for a given area ratio. In the case of the latter line, there is no difference between the parallel and diverging diffuser. Ishikawa and Nakamura (1989)[13] also attempted to compare their results with those of Sovran and Klomp[27] for a conventional annular diffuser for the same wall length and area ratio, their diffuser was superior, but since the inlet conditions were different in the 10
- 24. Literature Review Chapter2 two studies, this conclusion is only tentative. It was also found that the addition of a conical center body improves the performance of simple conical diffusers with appreciable or large stall. The study carried out by Moller (1965) [23], [24], who designed an axial to radial band with the intention of eliminating diffusion in the inlet region, found that the peak pressure recovery for the entire band and radial diffuser sections was 0.88 and 0.82 for the low blockage and high blockage cases, respectively. Cockrell and Markland [5] reported that a variation in the area ratio from 2.5 to 8.0 has a small effect on the loss coefficients of conical diffusers. 2.1.2 Wall Contouring Several annular diffuser studies have been published in which contoured walls were an essential part of the design problem. Thayer (1971) [35] reported that curved wall diffusers had pressure recovery as high as 0.61 to 0.65 for an area ratio of 2.15. An extensive study by Stevens and Williams [31], [32], reported that for curved wall diffuser, good pressure recovery was found for a loss significantly below the level which would be expected from pressure recovery loss correlation , but pressure recovery values were lower then those which would be expected from the Sovran and Klomp[27] map. Upon careful examination, it was determined that the boundary layers in this diffuser are different from those which would be expected in most diffuser studies. Takehira et al (1977) [34] presented extensive data for a large set of both straight annular diffusers and curved wall diffusers, and determined that the use of strong curvature at the exit of diffuser was not debilitating but did produce a penalty compared to noncurved diffusers or diffusers with curvature at the inlet. An additional study by Japikse [14], [17], shows that wall contouring is an important parameter regarding pressure recovery. Adkins et al (1983) [2], [3], tested an annular diffuser of constant outer radius and a conical center body with cones of different angles. In general the pressure recovery increases with decreasing cone angle for various area ratios, but the 132º and sometimes the 45º cone angle produced lower pressure recoveries than an equivalent sudden expansion. This was attributed to a large and rapid separation at the base of the cone where the diffuser starts. Adding a radius to the base of the cone so that it smoothly blended into the upstream hub, was found to improve the performance. 11
- 25. Literature Review Chapter2 2.2 Effects of Flow Parameters 2.2.1 Aerodynamic Blockage The aerodynamic blockage on annular diffusers is much less well understood than it is in channel and conical diffusers. Coladipietro et al (1974) [6] reported that for short diffusers, the variation of pressure recovery with blockage was similar to the channel and conical diffusers; that is the pressure recovery decreased with increasing blockage. However, for the long diffusers, higher performance was observed at the higher blockage levels. Stevens and Williams (1980) [31] determined that pressure recovery initially decreases with increased blockage but then for very long inlet lengths where the flow is able to achieve a fully developed form, the pressure recovery again rises. From a careful study of these data it is evident that not only the inlet boundary layer displacement thickness but also other higher order effects such as turbulence intensity and boundary layer mixing phenomena can greatly alter the measured result. In another study by Geobel and Japikse (1981) [8] found that the pressure recovery reduces as aerodynamic blockage increases. In concluding this section several notes can be made. First, the influence of inlet conditions on annular diffuser performance is more complicated than for channel and conical diffuser. In this case, both the hub and casing surfaces can develop boundary layers with significantly different histories. The two differing boundary layers will experience different growth processes as they pass through the diffuser. Furthermore, blockage on one wall has the effect of modifying the effective flow area and hence the core flow velocity, thereby influencing the growth of the boundary layer on the opposite wall. Hence complex interactions can develop within the diffuser. 2.2.2 Inlet Swirl The method of swirl generation can itself influence the performance of an annular diffuser and, therefore, consideration must be given first to this question. Most investigators have chosen to generate swirled in a radial inflow plane in order to take advantage of the simple cascade design geometry. Others have preferred to use axial cascade which have the advantage that they more closely simulate specific turbomachinery flow condition and permit control of the spacing between the diffuser and 12
- 26. Literature Review Chapter2 the vanes in form that may be more typical of an actual turbo machine. On the other hand axial cascade invariably introduces tip and hub leakage since the cascades are of a variable geometry type, an effective sealing is impossible. In addition to inlet swirl, there may be changes in inlet turbulence intensity, velocity or total pressure gradients, vorticity or wake shading, and inlet aerodynamic blockage may change indirectly as a function of the swirl angle as it is varied. In order for firm conclusion to be drawn, the effect of swirl variation must be deciphered from the performance data. Srinath (1968) [28] considered an axial flow equiangular diffuser with swirl between 0º and 15º. Peak pressure recovery was found at approximately 10º and then decreased rapidly. Hoadley and Hughes (1969) [11] tested an annular diffuser with a cylindrical inner body and reported that best recovery was achieved at approximately 10º of swirl. Dovzhik and Kartavenko (1975) [7] also reported by the same type of study that the best performance can be achieved between the range of 10º to 20º of inlet swirl angle. A study is presented by Japikse and Pamprreen (1979) [15]of an exhaust diffuser and hood found that substantial recovery has been achieved even up to swirl angle in excess of 40º. 2.2.3 Inlet Turbulence With long approach pipes diffuser performance rises as approach length increases. This was first noted in the Cockrell and Markland [5] and attributed this to changes in turbulence which enhances mixing transverse to flow directions, thus reducing the distortions. Indeed, the core turbulence intensity of developing pipe flow rises significantly from La /D is equal to 20 to 45 and than remains nearly constant. Two studies have been published which considered variation in inlet turbulence intensity or structure for there impact on annular diffuser performance. The data of Coladieiepro et al (1974) [6] have included both low and high inlet turbulence intensity levels, and this may be explanation for the unusual measurements observed at different blockage. The second study is the work of Williams and Stevens (1969) [32] and Stevens and Fry (1973) [33] , which showed that substantial improvements in radial momentum transport were achieved by turbulence producing grids and wall spoilers. Additional results by Hestermann et al (1995) [9], and Klein (1995) [22] also show that increasing the level of turbulence to 6 – 8.5 % is beneficial in increasing the pressure recovery and, in one case of removing the separation of stalled diffuser. The conclusion of above study is that the effect of increasing inlet turbulence intensity is to increase pressure recovery. 13
- 27. Literature Review Chapter2 2.2.4 Mach Number Influence Most annular diffuser research has been carried out at low inlet mach numbers. However, several studies have shown measurement at different Mach number. The study by Thayer (1971) [35], Wood and Henry (1958) [36] and Japikse and Pampreen (1979) [15] illustrate virtual independence of recovery with Mach number up to some critical level of approximately 0.80 to 1.1. The actual level depends on method of measurement and the type of inlet. Wood and Henry [36] show that a shock structure must be presented before the performance begins to deteriorate, but the reference Mach number may have little to do with the actual shock location and shock structure. In most cases, the reduction of performance with Mach number is very slight but in a few cases there can be a degradation of five or ten point of performance recovery. 2.2.5 Reynolds Number Influence Viscosity is an important parameter in any fluid dynamic process and normally appears in the form of a Reynolds number. Typically, diffusers are characterized by a Reynolds number based on an inlet hydraulic diameter. All studies reported that the Reynolds number is a comparatively weak parameter as long as the flow is in the fully turbulent regime. Crockrell and Markland (1963)[5] state that a variation of the inlet Reynolds number has no significant effect on the diffuser performance if this variation is uncoupled from its effects on the inlet boundary layer parameters. For Reynolds number variation within the range of 2×104–7×105, they also pointed out that the diffuser performance would be practically independent of Reynolds number provided the inlet boundary parameters remain constant. Sharan (1972) [26] reported that for thick boundary layers, there is no change in pressure recovery as the Reynolds number increases. 2.3 Boundary Layer Parameter The flow in diffuser is governed by the behavior of the boundary layers at the diffuser walls. The deceleration of the flow through the diffuser produces a pressure rise in the stream wise direction. The wall shear layers are therefore subjected to a positive or adverse pressure gradient. As is well known, an adverse pressure gradients cause the wall boundary layers to thicken and possibly separate from the diffuser walls, forming areas of backflow in the diffuser. The net result of thinking of the wall boundary layers or the formation of regions of backflow, is the blockage of flow area which reduces the effective 14
- 28. Literature Review Chapter2 area available to the flow. Reduction in effective flow area in turn results in a reduced pressure rise through the diffuser. 2.3.1 Boundary Layer Suction The effect of suction consists in the removal of decelerated fluid particles from the boundary layer before they are given a chance to cause separation. Wilbur and Higginbotham (1957) [30], investigated the suction phenomenon and found that a suction flow rate of 2.3% increased the static pressure rise by 25 – 60% and decreased the measured total pressure loss by 63%. In another study by Wilbur and Higginbotham (1955) [29], it is shown that suction control is not efficient when applied in an extensive backflow region such as exists immediately downstream of an abruptly turned body. Experiments by Juhasz (1974) [20], on short annular diffuser showed that the diffuser exit profiles could be shifted either towards the hub or towards the casing of annulus by bleeding off a small fraction of the flow through the inner and outer wall respectively. Boundary Layer Suction is also adopted by Ackert (1967) [1], for both channel and conical diffuser with large divergence angle. 2.3.2 Blowing and Injection Wilbur and Higginbotham (1955) [29], found that at an injection rate of 3.4%, a 33% increases in the measured static pressure rise and a 50% decrease in the measured total pressure loss can be obtained. Juhasz (1974) [20], have reported results of their investigations on the effect of injecting secondary fluid into wild angle conical diffusers through annular slot at inlet. Injection was found to result in considerable improvement in the uniformity of exit flow as well as in the magnitude of pressure recovery. 15
- 29. Chapter 3 CFD Analysis in FLOTRAN
- 30. CFD Analysis FLOTRAN Chapter 3 FLOTRAN is a finite element analysis program for solving fluid flow and conjugate heat transfer problems. The fluid flow problem is defined by the laws of conservation of mass, momentum, and energy. These laws are expressed in terms of partial differential euations which are discretized with a finite element based technique. Assumptions about the fluid and the analysis are as follows: 1 There is only one phase. 2 The user must determine: (a) If the problem is laminar (default) or turbulent (b) If the incompressible (default) or the compressible algorithm must be invoked. The governing equations solved by FLOTRAN are the Navier-Stokes equations combined with the continuity equation, the thermal transport equation, and constitutive property relationships. Navier-Stokes Equation yxpyVVxUU∂ ∂ + ∂ ∂ −= ∂ ∂ + ∂ ∂τρρ 11 Continuity Equation ()()()0= ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ zVzyVxVtyxρρρρ This equation represents a number of fluid flow equations: φ Equation D S 1 mass conserve. 0 u x-momentum μ xgxPρ+ ∂ ∂ − v y-momentum μ xgxPρ+ ∂ ∂ − w z-momentum μ xgxPρ+ ∂ ∂ − T temp.(energy) k q k turb.k.e. ttσμ ρεμ−Gt ε t. k.e. diss. rate ttσμ kCGkCt221 ερεμ− jiijjixuxuxuG∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = 17 ________________________________________________________________________
- 31. CFD Analysis FLOTRAN Chapter 3 3.1FLOTRAN Features • Steady-State or Transient Solution Algorithm • Equal Order Approximation for Velocity and Pressure 1. No staggered grids 2. No mixed order interpolation • Monotone Streamline Upwind Approximation for Advection Terms 1. Increased accuracy over conventional upwind 2. Stable at high Reynolds numbers • Minimal Execution Time Requirements 1. Segregated sequential solution 2. Iterative solution methods • Minimal Storage Requirements 1. Bandwidth independent 2. In-core solution method 3.2 FLOTRAN Capabilities • 2-D or 3-D Geometries • Ax symmetric Geometries • Laminar or Turbulent Flow and/or Heat Transfer • Forced, Free, or Mixed Convection • Conduction • Conjugate Heat Transfer • Distributed Flow Resistances • Porous Media • Incompressible or Compressible Flow • Steady State or Transient • Total Energy Equation • Global Convergence Status • Boundary Conditions: 1. Prescribed Nodal Values - Velocity, Pressure, Temperature, Turbulent Kinetic Energy, Turbulent Energy Dissipation. 2. Prescribed Heat Flux 3. Prescribed Heat Source 18 ________________________________________________________________________
- 32. CFD Analysis FLOTRAN Chapter 3 4. Prescribed Film Coefficient 5. Adiabatic 6. Symmetry 7. Periodic Boundaries 3.3 Getting Started Using FLOTRAN FLOTRAN has been integrated with ANSYS. This integration allows users to build the finite element models using ANSYS PREP7 and to pass the model data to flotran for the various analyses. Once the FLOTRAN analyses are done, the data can then be transferred to the ANSYS postprocessor, POST1. IDEAS and PATRAN can also be used to pre- and postprocess finite element models for FLOTRAN analyses. In this course, we will use only ANSYS for pre- and postprocesses. 3.3.1 FLOTRAN Processes • Preprocessing (or model generation and B.C./I.C.) - ANSYS, • Solution - FLOTRAN, • Postprocessing (or results evaluation) - ANSYS. 3.3.2 FLOTRAN Modeling Only two element types are valid for FLOTRAN analyses. FLOTRAN uses the MAT element attribute to distinguish fluid elements from solid elements. Fluid elements must have MAT = 1, and solid elements are identified by MAT > 1. The REAL ATTRIBUTE is to flag elements with distributed resistance. 3.3.2.1 Modeling Constraints • Element Types 1. Quad and triangles (2D) - PLANE55 2. Hex and tet (3D) - SOLID70 • Element Material Number 1. MAT = 1 - Fluid Elements 2. MAT > 1 - Solid Elements • Cartesian Coordinates • Rotating Coordinates 19 ________________________________________________________________________
- 33. CFD Analysis FLOTRAN Chapter 3 • Cylindrical Coordinates 3.3.2.2 Modeling Guidelines • Examine the solution domain for possible symmetries • Sketch the geometry for planning the geometry model and the finite element model • Anticipate the analysis requirements 1. Regions of high gradients in the solution variables. These regions usually require finer meshes. 2. Important Boundaries such as flow inlets, flow exits, heated areas, and constant temperature boundaries. 3. Mesh size requirements to be considered with maximum limit of nodes and CPU and storage requirements. • Sketch the proposed mesh. • Construct the geometry and elements with top-down or bottom-up technique. 3.3.2.3Boundary Condition Types • Symmetry boundaries o Geometry half symmetry or Mirror image o Align with a coordinate axis o Zero normal velocity on the boundaries • Inflow boundaries - specify either inlet velocity or pressure • Outflow boundaries - specify pressure only • Wall boundaries - zero flow velocity on the wall • Periodic Boundaries - corresponding boundaries with identical flows • Thermal boundary conditions - do not affect flow boundary conditions • Initial conditions - specified with separate boundary condition in each LOAD STEP(ANSYS) 3.3.2.4 Optimum Order for Setting Boundary conditions • Symmetry boundaries • Inflow boundaries • Outflow boundaries 20 ________________________________________________________________________
- 34. CFD Analysis FLOTRAN Chapter 3 • Wall boundaries When a boundary condition is repeatedly specified, the latter overwrite the former one. Unspecified flow boundaries are treated as natural boundary conditions where mass can enter or leave the boundaries. 3.3.3 FLOTRAN Solution A complete pass through all the equations is called a global iteration consisting of 1. Approximate solution of each momentum equation in sequential fasion. 2. Solution of the pressure equation. 3. Calculation of velocities to conserve mass. 4. Solution of the energy equation. 5. Update of the laminar properties. 6. Solution of the turbulence equations. 7. Update of the turbulent properties. The progress of the solution is monitored by observing the rate of change of the solution from one global iteration to the next. The analyst can restart the analysis until satisfied that the rate of change of the solution is small enough. The approximate solution of the momentum equation is obtained through the use of a tri-diagonal matrix algorithm. The momentum equations are relaxed to provide a stable solution. The pressure equation is solved with a pre-conditioned conjugate gradient routine. An incomplete Choleski decomposition provides the preconditioning. The approach is particularly well suited for practical applications because the solver requires very little storage other than those associated with the non-zero matrix terms in the nonsymmetric momentum equation. The performance of the method is bandwidth independent and it is ideally suited towards use with irregular and unstructured finite element grids. 3.3.3.1 Results Evaluation • Field Variable Information 1. Velocity 2. Pressure 3. Temperature 21 ________________________________________________________________________
- 35. CFD Analysis FLOTRAN Chapter 3 4. Total Temperature 5. Turbulent Kinetic Energy 6. Turbulent Dissipation Rate 7. Density 8. Molecular Viscosity 9. Effective Viscosity 10. Thermal Conductivity • Calculated Field Quantities 1. Stream Function (2D) 2. Velocity Magnitude (3D) 3. Wall Film Coefficients 4. Wall Heat Fluxes 5. Pressure Coefficient 6. Mach Number 7. Total Pressure 8. Nodal Heat Fluxes 9. Nodal Film Coefficients • Solution Reliability Statistics 1. Nodal Residuals 2. Nodal Error Indicators • Graphic Output: 1. All of the imaging capabilities (e.g., contour plots, vector plots, etc.) All FLOTRAN variables can be used for postprocessing. 2. Mass less Particle Tracking is available in the ANSYS and IDEAS programs. 3.3.4 FLOTRAN Postprocessing The FLOTRAN results file, <jobname&.res> is a unformatted binary file that can be read by the FLREAD command in ANSYS postprocessing. 3.3.4.1 Read Results File: FLREAD, jobname, ext where ext is the extension of FLOTRAN filename. 22 ________________________________________________________________________
- 36. CFD Analysis FLOTRAN Chapter 3 res Nodal results file for all degrees of freedom as well as properties nqh Heat flux and film coefficients eid Error indicator file Plot Results: PLNSOL, variable (Velocity, Temperature, Pressure, etc.) Plot velocity vectors: PLVECT, V Plot graphs along a line path: Define Path: LPTATH, node1, node2 ...node10 Define Name of Graph: PDEF, User-define-name, Variable Produce Graph: PLPATH, User-define-name Integrate Pressures: INTSRF, PRES Particles Tracing: Define up to 50 points in problem domain TRPOIN,x,y,z TRPOIN,PICK List existing points with TRPLIS Delete points with TRPDEL Execute particle tracing of any post processing variable PLTRAC, FLUID, item, compon 3D Contour Plots: /CTYPE,1 /EDGE,off 23 ________________________________________________________________________
- 37. CFD Analysis FLOTRAN Chapter 3 ASEL,S,EXT NSLA,S,ALL,1 NSEL,INVE PLNSOL,V,SUM 3D Cross Section Contour Plots /TYPE,3,SECT /FOCUS,3,RI,0,D4+RI /VIEW,3,1,0,0 NSEL,s,loc,x,RI ESLN,,0 PLNSOL,V,SUM PLNSOL,PRESS Transient results files use ANSYS POST26. 3.5 Error and Trouble Shooting FLOTRAN error message indicates a fatal error. FLOTRAN performs a number of data checks to ensure that the problem posted is valid. There are, of course, many inputs that cannot be verified; users must verify them. Diverging solution and unexpected results are often caused by invalid input. 3.5.1 Common Causes of Divergence • Incorrect problem setup o Highly skewed or tapered finite elements o Missing or duplicate nodes o Incorrect or missing boundary conditions o Unreferenced nodes o Poorly defined problem domain • Incorrect problem setup in FLOTRAN o Inconsistent property information o Invalid control parameters • Tough fluids problem 24 ________________________________________________________________________
- 38. CFD Analysis FLOTRAN Chapter 3 3.5.2 Trouble Shooting Guide • Users may check the boundary conditions by setting both Flow and Thermal in Screen 1S to F(false) and Iteration to 0. The FLOTRAN will generate a jobname.prt that tabulates the mass flows at all inlets and outlets. If unexpected inlets/outlets are listed, eliminate them. • Make sure information on Screen 2S and Screen 2P is realistic and consistent. For example, a temperature data given in when it should be given in may give an unrealistic density and cause divergence. • If the divergence occurs on the first little iteration, it is usually either a modeling error or an incorrect FLOTRAN data specification. If a FLOTRAN analysis runs for a short time (5-10 iterations) where it appears to converge and then diverges, it may be caused by improper run parameters. For example, a laminar flow analysis on a high Reynolds number situation may first converge then diverge. • Reducing the relaxation parameters on Screen 4S may help the convergence. These parameters are set at 0.5 and may be reduced to 0.2-0.3 to better control the convergence. Another alternative is to lower the inertia number on Screen 4S. If these methods still fail to converge, it may be possible to pre-condition the problem. This is done by raising the viscosity an appropriate order of magnitude to obtain a laminar solution and then introducing the turbulence. 3.6 FLOTRAN Applications FLOTRAN has been applied to a variety of applications from a wide range of industries. • AUTOMOTIVE 1. Study of air flow over vehicles 2. Passenger compartment flow 3. Fluid flow, conjugate heat transfer analysis of engine exhaust manifolds and water jackets - Flow through radiator passages 4. Flow analysis through various valve configurations • AEROSPACE 1. External flow over various wing configurations 2. Internal flow analyses of nozzles and ducts 3. Fluid flow, heat transfer analysis of aircraft passenger compartments 4. Compressible flow analysis with shock/boundary layer interaction 25 ________________________________________________________________________
- 39. CFD Analysis FLOTRAN Chapter 3 5. Thermal analyses • ELECTRONICS 1. Electronic cooling in a computer terminal 2. Conjugate heat transfer analysis of IC package 3. Heat transfer analysis of electronic fin array 4. Heat transfer analysis of a simulated card cage 5. Disk flow • POWER 1. Thermally stratified turbulent pipe flow 2. Pressurized thermal shock 3. Natural convection cooling 4. Fluid bed reactor analysis 5. Valve analysis • HVAC 1. Flow inside buildings 2. Flow in ducts 3. Flow in pipes 4. Flow through coolant passages 5. Heat exchanger analysis • TURBO MACHINERY 1. Torque converter flow analysis 2. Flow through vaned and vaneless diffusers 3. Labyrinth seal flow 4. Blade cooling analysis 5. Flow in pump, compressor, turbine, impeller passages 26 ________________________________________________________________________
- 40. Chapter 4 FLOTRAN Mathematical Model
- 41. FLOTRAN Mathematical Model Chapter 4 4.1 Fluid Flow Fundamentals This chapter discusses the FLOTRAN solution method used with elements fluid141 and fluid142. These elements are used for the calculation of 2-D and 3-D velocity and pressure distributions in a single phase, Newtonian fluid. Thermal effects, if present, can be modeled as well. The fluid flow problem is defined by the laws of conservation of mass, momentum, and energy. These laws are expressed in terms of partial differential equations which are discretized with a finite element based technique. Assumptions about the fluid and the analysis are as follows: 1. There is only one phase. 2. The user must determine: (a) if the problem is laminar (default) or turbulent; (b) if the incompressible (default) or the compressible algorithm must be invoked. 4.1.1. Continuity Equation From the law of conservation of mass law comes the continuity equation: yxpyVVxUU∂ ∂ + ∂ ∂ −= ∂ ∂ + ∂ ∂τρρ 11 ()()()0= ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ zVzyVxVtyxρρρρ (4–1) where: Vx, Vy and Vz = components of the velocity vector in the x, y and z directions, respectively ρ = density x, y, z = global Cartesian coordinates t = time The rate of change of density can be replaced by the rate of change of pressure and the rate at which density changes with pressure: tPPt∂ ∂ ∂ ∂ = ∂ ∂ρρ (4–2) where: P = pressure 28
- 42. FLOTRAN Mathematical Model Chapter 4 The evaluation of the derivative of the density with respect to pressure comes from the equation of state. If the compressible algorithm is used, an ideal gas is assumed: RTtRTP1= ∂ ∂ ⇒= ρρ (4–3) where: R = gas constant T = temperature If the incompressible solution algorithm is used (the default), the user can control the specification of the value with: βρ1= ∂ ∂ P (4–4) where: β = bulk modulus The default value of 1015 for β implies that for a perfectly incompressible fluid, pressure waves will travel infinitely fast throughout the entire problem domain, e.g. a change in mass flow will be seen downstream immediately. 4.1.2. Momentum Equation In a Newtonian fluid, the relationship between the stress and rate of deformation of the fluid (in index notation) is: iiijijjiIJijxuxuxuP∂ ∂ +⎟⎟ ⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ +−=λδμδτ (4–5) where: τij = stress tensor ui = orthogonal velocities (u1 = vx, u2 = vy, u3 = vz) μ = dynamic viscosity λ = second coefficient of viscosity The final term, the product of the second coefficient of viscosity and the divergence of the velocity, is zero for a constant density fluid and is considered small enough to neglect in a compressible fluid. Equation 4.5 transforms the momentum equations to the Navier- 29
- 43. FLOTRAN Mathematical Model Chapter 4 Stokes equations; however, these will still be referred to as the momentum equations elsewhere in this chapter. The momentum equations, without further assumptions regarding the properties, are as follows: ()()()() xxexexexxxzxyxxxTzVzyVyxVxRxPgzVVyVVxVVtV+⎟⎠ ⎞ ⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎠ ⎞ ⎜⎝ ⎛ ∂ ∂ ∂ ∂ ++ ∂ ∂ −= ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ μμμρρρρρ (4–6) ()()()() yyeyeyeyyyzyyyxyTzVzyVyxVxRyPgzVVyVVxVVtV+⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ ++ ∂ ∂ −= ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ μμμρρρρρ (4–7) ()()()() zzezezezzzzzyzxzTzVzyVyxVxRzPgzVVyVVxVVtV+⎟⎠ ⎞ ⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎠ ⎞ ⎜⎝ ⎛ ∂ ∂ ∂ ∂ ++ ∂ ∂ −= ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ μμμρρρρρ (4–8) where: gx, gy, gz = components of acceleration due to gravity ρ = density μe = effective viscosity Rx, Ry, Rz = distributed resistances Tx, Ty, Tz = viscous loss terms For a laminar case, the effective viscosity is merely the dynamic viscosity, a fluid property. The effective viscosity for the turbulence model is described later in this section. The terms Rx, Ry Rz represent any source terms the user may wish to add. An example is distributed resistance, used to model the effect of some geometric feature without modeling its geometry. Examples of this include flow through screens and porous media. The terms Tx, Ty Tz are viscous loss terms which are eliminated in the incompressible, constant property case. The order of the differentiation is reversed in each term, reducing the term to a derivative of the continuity equation, which is zero. xzyxTxVzxVyxVx=⎟⎠ ⎞ ⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎠ ⎞ ⎜⎝ ⎛ ∂ ∂ ∂ ∂ μμμ (4–9) 30
- 44. FLOTRAN Mathematical Model Chapter 4 yzyxTyVzyVyyVx=⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ μμμ (4–10) zzyxTzVzzVyzVx=⎟⎠ ⎞ ⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎠ ⎞ ⎜⎝ ⎛ ∂ ∂ ∂ ∂ μμμ (4–11) The conservation of energy can be expressed in terms of the stagnation (total) temperature, often useful in highly compressible flows, or the static temperature, appropriate for low speed incompressible analyses. 4.1.3. Compressible Energy Equation The complete energy equation is solved in the compressible case with heat transfer In terms of the total (or stagnation) temperature, the energy equation is: ()()()() tPQEWzTKzyTKyxTKxTCVzTCVyTCVxTCtVKVoooopzopyopxoP∂ ∂ +Φ++++⎟⎠ ⎞ ⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎠ ⎞ ⎜⎝ ⎛ ∂ ∂ ∂ ∂ = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ ρρρρ (4–12) where: Cp = specific heat To = total (or stagnation) temperature K = thermal conductivity Wv = viscous work term Qv = volumetric heat source Φ = viscous heat generation term Ek = kinetic energy The static temperature is calculated from the total temperature from the kinetic energy: pocvTT22−= (4–13) where: T = static temperature v = magnitude of the fluid velocity vector The static and total temperatures for the non-fluid nodes will be the same. 31
- 45. FLOTRAN Mathematical Model Chapter 4 The Wv, Ek and Φ terms are described next. The viscous work term using tensor notation is: ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ = xuWiVμ (4–14) where the repetition of a subscript implies a summation over the three orthogonal directions. The kinetic energy term is ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ = jkkijiiVxuxxuxuWμ (4–15) Finally, the viscous dissipation term in tensor notation is kiikkixuxuxu∂ ∂ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ =μφ (4–16) In the absence of heat transfer (i.e., the adiabatic compressible case), equation 4–13 is used to calculate the static temperature from the total temperature specified. 4.1.4. Incompressible Energy Equation The energy equation for the incompressible case may be derived from the one for the compressible case by neglecting the viscous work (Wv), the pressure work, viscous dissipation (f), and the kinetic energy (Ek). As the kinetic energy is neglected, the static temperature (T) and the total temperature (To) are the same. The energy equation now takes the form of a thermal transport equation for the static temperature: ()()()() VpzpypxpQzTKzyTKyxTKxTCVzTCVyTCVxTCt+⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ ρρρρ (4–17) 4.1.5. Turbulence If inertial effects are great enough with respect to viscous effects, the flow may be turbulent. The user is responsible for deciding whether or not the flow is turbulent. Turbulence means that the instantaneous velocity is fluctuating at every point in the flow 32
- 46. FLOTRAN Mathematical Model Chapter 4 field. The velocity is thus expressed in terms of a mean value and a fluctuating component: rxxxVVV+= − (4–18) where: xV= mean component of velocity in x-direction rxV= fluctuating component of velocity in x-direction If an expression such as this is used for the instantaneous velocity in the Navier-Stokes equations, the equations may then be time averaged, noting that the time average of the fluctuating component is zero, and the time average of the instantaneous value is the average value. The time interval for the integration is arbitrarily chosen as long enough for this to be true and short enough so that “real time” transient effects do not affect this integration. ∫= tdtVtrx δδ001; −∫=xxVdtVttδ δ01 (4–19) After the substitution of Equation 4–18 into the momentum equations, the time averaging leads to additional terms. The velocities in the momentum equations are the averaged ones, and we drop the bar in the subsequent expression of the momentum equations, so that the absence of a bar now means the mean value. The extra terms are: ()()()rzrxryrxrxrxRxVVzVVyVVx ρρρσ ∂ ∂ − ∂ ∂ − ∂ ∂ −= (4–20) ()()()rzryryryrxryRyVVzVVyVVx ρρρσ ∂ ∂ − ∂ ∂ − ∂ ∂ −= (4–21) ()()()rzrzryrzrxrzRzVVzVVyVVx ρρρσ ∂ ∂ − ∂ ∂ − ∂ ∂ −= (4–22) where: σR = Reynolds stress terms In the eddy viscosity approach to turbulence modeling one puts these terms into the form of a viscous stress term with an unknown coefficient, the turbulent viscosity. For example: 33
- 47. FLOTRAN Mathematical Model Chapter 4 yVVVxtyx∂ ∂ =−μρ (4–23) The main advantage of this strategy comes from the observation that the representation of σR is of exactly the same form as that of the diffusion terms in the original equations. The two terms can be combined if an effective viscosity is defined as the sum of the laminar viscosity and the turbulent viscosity: teμμμ+= (4–24) The solution to the turbulence problem then revolves around the solution of the turbulent viscosity. Note that neither the Reynolds stress nor turbulent heat flux terms contain a fluctuating density because of the application of Favre (37) averaging to equation 4–20 to equation 4–22. Bilger(37) gives an excellent description of Favre averaging. Basically this technique weights each term by the mean density to create a Favre averaged value for variable φ which does not contain a fluctuating density: ρρφφ=~ (4–25) The tilde indicates the Favre averaged variable. For brevity, reference is made to Bilger(37) for further details. There are eight turbulence models available in FLOTRAN . The model acronyms and names are as follows: • Standard k-ε Model • Zero Equation Model • RNG - (Re-normalized Group Model) • NKE - (New k-ε Model due to Shih) • GIR - (Model due to Girimaji) • SZL - (Shi, Zhu, Lumley Model) • Standard k-ω Model • SST - (Shear Stress Transport Model) The simplest model is the Zero Equation Model, and the other five models are the two equation standard k-ε model and four extensions of it. The final two models are the 34
- 48. FLOTRAN Mathematical Model Chapter 4 Standard k-ω Model and SST model. In the Zero Equation Model, the turbulent viscosity is calculated as: Φ=2sLcρ (4–26) where: μt = turbulent viscosity Φ = viscous dissipation (Equation 4–16) ⎪⎩ ⎪⎨ ⎧ ≤ ⎭⎬⎫ ⎩⎨⎧ > = 0.009.04.0min0.0xcnxxsLifLLLifLL Lx = length scale Ln = shortest distance from the node to the closest wall Lc = characteristic length scale In the k-ε model and its extensions, the turbulent viscosity is calculated as a function of the turbulence parameters kinetic energy k and its dissipation rate ε using Equation 4–27. In the RNG and standard models, Cμ is constant, while it varies in the other models. ερμμ 2kCt= (4–27) where: Cμ = turbulence constant k = turbulent kinetic energy (input/output as ENKE) ε = turbulent kinetic energy dissipation rate (input/output as ENDS) In the k-ω model and SST model, the turbulent viscosity is calculated as: ωρμkt= (4.28) Here ω is defined as: kCμεω= (4.29) where: ω = specific dissipation rate The k-ε model and its extensions entail solving partial differential equations for turbulent kinetic energy and its dissipation rate whereas the k-ω and SST models entail solving 35
- 49. FLOTRAN Mathematical Model Chapter 4 partial differential equations for the turbulent kinetic energy and the specific dissipation rate. The equations below are for the standard k-ε model. The different calculations for the other k-ε models will be discussed in turn. The basic equations are as follows: 4.1.5.1. Standard k-ε Model The reader is referred to Spalding and Launder (37) for details. The Turbulent Kinetic Energy equation is: ()()() ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ +−Φ+ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ zTgyTgxTgCzkzykyxkxzkpVykpVxkpVtpkzyxtttktktktzyx σβμρεμσμσμσμ 4 (4.30) The Dissipation Rate equation is: ()()() () ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂− +−Φ+ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ ∂ ∂ = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ zTgyTgxTgkCCkCkCzzyyxxzpVypVxpVtpzyxttktktktzyx σβρερεεμεσμεσμεσμεεεεμ32211 (4.31) The final term in each equation are terms used to model the effect of buoyancy and are described by Viollet (37). Default values for the various constants in the standard model are provided by Lauder and Spaldingand (37) are given in "Standard Model Coefficients". The solution to the turbulence equations is used to calculate the effective viscosity and the effective thermal conductivity: ερμμα 2kCe+= (4–32) tpteCkk σμ += (4–33) where: μe = effective viscosity 36
- 50. FLOTRAN Mathematical Model Chapter 4 Ke = effective conductivity σt = Turbulent Prandtl (Schmidt) Number The four extensions to the standard k-ε model have changes in either the Cμ term or in the source term of the dissipation equation. The new functions utilize two invariants constructed from the symmetric deformation tensor Sij, and the antisymmetric rotation tensor Wij. These are based on the velocity components vk in the flow field. ()ijjiijVVS1121+= (4–34) ()mijmrijjiijCVVWεΩ+−= 1121 (4–35) where: Cr = constant depending on turbulence model used Ωm = angular velocity of the coordinate system εmij = alternating tensor operator The invariants are: ijijSSk2 εη= (4–36) and ijijWWk2 εξ= (4–37) 4.1.5.2. RNG Turbulence Model In the RNG model, the constant C1ε in the dissipation Equation 4–31, is replaced by a function of one of the invariants. 311142.1 βηηηηαε+ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ − −=C (4–38) In the RNG model a constant Cμ is used. The value is specified with a separate command than the one used to specify the Cμ in the standard model. The same is true of the constant C2. As shown in the above table, the diffusion multipliers have different values than the 37
- 51. FLOTRAN Mathematical Model Chapter 4 default model, and these parameters also have their own commands for the RNG model. The value of the rotational constant Cr in the RNG model is 0.0. Quantities in Equation 4–31 not specified in Table 4.2: "RNG Model Coefficients" are covered by Table 4.1: "Standard Model Coefficients". 4.1.5.3. NKE Turbulence Model The NKE Turbulence model uses both a variable Cμ term and a new dissipation source term. The Cμ function used by the NKE model is a function of the invariants. (4–39) The production term for dissipation takes on a different form. From equation 4.31, the production term for the standard model is: ΦkCt εμε1 (4–40) The NKE model replaces this with: ερεijijSSC21 (4–41) The constant in the dissipation rate Equation 4–31 is modified in the NKE model to be: ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ + = 5max11ηηεMCC (4–42) The constant C2 in the dissipation Equation 4–31 of the NKE model has a different value than that for the corresponding term in the standard model. Also, the values for the diffusion multipliers are different. Commands are provided for these variables to distinguish them from the standard model parameters. So for the NKE model, the input parameters are as follows: The value of the rotational constant Cr in the NKE model is 3.0. All parameters in Equation 4–30 and Equation4–31 not covered by this table are covered in Table 4.1: "Standard Model Coefficients" 4.1.5.4. GIR Turbulence Model The Girimaji model relies on a complex function for the calculation of the Cμ coefficient. The coefficients in Table 4.4: "GIR Turbulence Model Coefficients" are used. 38
- 52. FLOTRAN Mathematical Model Chapter 4 These input values are used in a series of calculations as follows First of all, the coefficients to L01L4 have to be determined from the input coefficients. Note, these coefficients are also needed for the coefficients of the nonlinear terms of this model, which will be discussed later. 322;1:12221111 0101−=+=−=CLCLCL 12;124433−=−=CLCL (4–43) Secondly, the following coefficients have to be calculated: ()()() () 274;2792271; 33121211272cos21; 21232321242232211 2201211 23211 220111 201abDrpqpbpqCLLLLLLqabarcLLLrLLp+=+−=−= ⎥⎦ ⎤ ⎢⎣ ⎡+−+ ⎟⎠ ⎞ ⎜⎝ ⎛ = − − =Θ⎟⎠ ⎞ ⎜⎝ ⎛ = − = ζηηηηη (4–44) With these coefficients we can now determine the coefficient Cμ from the following set of equations: ()()() ⎪⎪⎪⎪⎪ ⎩ ⎪⎪⎪⎪⎪ ⎨ ⎧ <<⎟⎠ ⎞ ⎜⎝ ⎛+ − +− <<⎟⎠⎞ ⎜⎝ ⎛− +− >⎟⎠ ⎞ ⎜⎝ ⎛+−+⎟⎠ ⎞ ⎜⎝ ⎛+−+− ==⎥⎦⎤ ⎢⎣ ⎡+−− = 0,0323cos3230,03cos32302230031313111 242232201201bDifapbDifapDifDbDbporLifLLLLLC πθθηζημ (4–45) and for the GIR model, the rotational term constant Cr is 2444− − = CCCr (4–46) 39
- 53. FLOTRAN Mathematical Model Chapter 4 4.1.5.5. SZL Turbulence Model The Shi-Zhu-Lemley turbulence model uses a simple expression for the Cμ coefficient and uses the standard dissipation source terms. The user controls three constants in the calculation of the coefficients: ζημ 321sssAAAC++ = (4–47) The constants and their defaults are as follows: The value of the rotational constant Cr for the SZL model is 4.0. 4.1.5.6. Standard k-ω Model The k-ω model solves for the turbulent kinetic energy k and the specific dissipation rate ω (Wilcox(37)). As in the k-ε based turbulence models, the quantity k represents the exact kinetic energy of turbulence. The other quantity ω represents the ratio of the turbulent dissipation rate ε to the turbulent kinetic energy k, i.e., is the rate of dissipation of turbulence per unit energy. The turbulent kinetic energy equation is: ()()() ⎟⎟⎠ ⎞ ⎜⎜⎝⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ +−Φ+ ⎥⎦ ⎤ ⎢⎣ ⎡ ∂ ∂ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ + ∂ ∂ +⎥⎦⎤ ⎢⎣ ⎡ ∂ ∂ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ + ∂ ∂ +⎥⎦ ⎤ ⎢⎣ ⎡ ∂ ∂ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ + ∂ ∂ = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ zTgyTgxTgCkCzkzykyxkxzkpVykpVxkpVtpkzyxkttktktktzyx σβμωρμσμμσμμσμμμ 42 (4–48) The specific dissipation rate equation is: () ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂− +′−Φ+ ⎥⎦ ⎤ ⎢⎣ ⎡ ∂ ∂ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ + ∂ ∂ +⎥⎦ ⎤ ⎢⎣ ⎡ ∂ ∂ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ + ∂ ∂ +⎥⎦ ⎤ ⎢⎣ ⎡ ∂ ∂ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ + ∂ ∂ = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ zTgyTgxTgCzzyyxxzVyVxVtpzyxttttzyx σβρρωβγρωσμμωσμμωσμμωωωωωωω 321 (4–49) The final term in Equation 4–48 and Equation 4–49 is derived from the standard k-ε model to model the effect of buoyancy. Default values for the model constants in the k-ω model are provided by Wilcox(37). Some values are the same with the standard k-ε model and are thus given in Table 4.1: "Standard Model Coefficients", whereas the other values are given in Table 46: "The k-ω Model Coefficients". The k-ω model has the advantage near the walls to predict the turbulence length scale accurately in the presence of adverse pressure gradient, but it suffers from strong 40
- 54. FLOTRAN Mathematical Model Chapter 4 sensitivity to the free-stream turbulence levels. Its deficiency away from the walls can be overcome by switching to the k-ε model away from the walls with the use of the SST model. 4.1.5.7. SST Turbulence Model The SST turbulence model combines advantages of both the standard k-ε model and the k-ω model. As compared to the turbulence equations in the k-ω model, the SST model first modifies the turbulence production term in the turbulent kinetic energy equation. From Equation 4.48, the production term from the k-ω model is: Φ=ttPμ (4–50) The SST model replaces it with: ()εμmtttCP1,minΦ= (4–51) By default, the limiting value of Clmt is set to 1015, so Equation 4–51 is essentially the same with Equation 4–50. However, Equation 4–51 allows the SST model to eliminate the excessive build-up of turbulence in stagnation regions for some flow problems with the use of a moderate value of Clmt. Further, the SST model adds a new dissipation source term in the specific dissipation rate equation: () ⎥⎦ ⎤ ⎢⎣ ⎡ ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂− zzkyykxxkFzωωωωρσω211 (4–52) Here, F1 is a blending function that is one near the wall surface and zero far away from the wall. The expression of the bending function F1 is given by Menter(37), and with the help of F1, the SST model automatically switches to the k-ω model in the near region and the k-ε model away from the walls. The model coefficients are all calculated as functions of F1: ()21111ϕϕϕFF−+= (7–53) Here, φ stands for the model coefficient (σk, σω, β΄, γ) of the SST model, and φ1 and φ2 stand for the model coefficient of the k-ω model and the k-ε model respectively. Default values for the various constants in the SST model are provided by Menter(37), and are given in Table 4.7: "The SST Model Coefficients". 4.1.5.8. Near-Wall Treatment All of the above turbulence models except the Zero Equation Model use the near-wall 41
- 55. FLOTRAN Mathematical Model Chapter 4 treatment discussed here. The near-wall treatment for the k-ω model and SST model are slightly different from the following discussions. The k-ε models are not valid immediately adjacent to the walls. A wall turbulence model is used for the wall elements. Given the current value of the velocity parallel to the wall at a certain distance from the wall, an approximate iterative solution is obtained for the wall shear stress. The equation is known as the “Log-Law of the Wall” ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ρτνδκρτ EVln1tan (4–54) where: vtan = velocity parallel to the wall τ = shear stress ν = kinematic viscosity (m/r) κ = slope parameter of law of the wall E = law of the wall constant δ = distance from the wall The default values of κ and E are 0.4 and 9.0 respectively, the latter corresponding to a smooth wall condition.From the shear stress comes the calculation of a viscosity: tanV τδμϖ= (4–55) The wall element viscosity value is the larger of the laminar viscosity and that calculated from Equation 4–55. Near wall values of the turbulent kinetic energy are obtained from the k-ε model. The near wall value of the dissipation rate is dominated by the length scale and is given by Equation 4–56. ()() κδεμ 5.175.0nWnWkC= (4–56) where: εnw = near wall dissipation rate knw = near wall kinetic energy 42
- 56. FLOTRAN Mathematical Model Chapter 4 The user may elect to use an alternative wall formulation (accessed with the FLDATA24,TURB,WALL,EQLB command) directly based on the equality of turbulence production and dissipation. This condition leads to the following expression for the wall parameter y+ μδκρμ 2141nWCy=+ (4–57) The wall element effective viscosity and thermal conductivity are then based directly on the value of y+. The laminar sub layer extends to (input on the + tyFLDATA24,TURB,TRAN command) with the default being 11.5. For y+ < + ty kkeffeff= =μμ (4–58) For y+ ≥ : + ty ()+ + = yEyeffln1 κμμ (4–59) ⎟⎠⎞ ⎜⎝ ⎛+ = + + fntpeffPyEyCkln1 κμσ (4–60) where: n = natural logarithm () () 4121Pr/1Pr4sin4⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ −⎟⎠ ⎞ ⎜⎝ ⎛= ttfnAP σσκππ Pr = Prandtl number Although the wall treatment should not affect the laminar solution, the shear stress calculation is part of the wall algorithm. Thus, shear stresses from the equilibrium model will differ slightly from those obtained from the default treatment, as described in Equation 4–54 thru equation 4.56. 43
- 57. FLOTRAN Mathematical Model Chapter 4 4.1.6. Pressure For numerical accuracy reasons, the algorithm solves for a relative pressure rather than an absolute pressure. Considering the possibility that the equations are solved in a rotating coordinate system, the defining expression for the relative pressure is: {}{}{}{}{}(rrrgPPPrelrefabs⋅××+⋅−+=ωωρρ0021 ) { } (4–61) where: ρo = reference density (calculated from the equation of state defined by the property type using the nominal temperature (input using FLDATA14 command)) Pref = reference pressure (input using FLDATA15 command) {g} = acceleration vector due to gravity (input using ACEL command) Pabs = absolute pressure Prel = relative pressure {r} = position vector of the fluid particle with respect to the rotating coordinate system {ω} = constant angular velocity vector of the coordinate system (input using CGOMGAcommand) Combining the momentum equations (equation 4.6 through equation 4.8) into vector form and again considering a rotating coordinate system, the result is: {}{}{}{}{}{}{}{}VPgrVDtVDabs22∇+∇−=××+×+μρωωρωρρ (4–62) where: {V} = vector velocity in the rotating coordinate system μ = fluid viscosity (assumed constant for simplicity) ρ = fluid density In the absence of rotation, {V} is simply the velocity vector in the global coordinate system. The negative of the gradient of the absolute pressure is: {}{}{}{}{}rrgPPrelabs××+⋅−−∇=∇−ωωρρ00 (4–63) Inserting this expression into the vector form of the momentum equation puts it in terms of the relative pressure and the density differences. 44
- 58. FLOTRAN Mathematical Model Chapter 4 {}{}{}(){}{}{}(){}{}VPgrVDtVDrel2002∇+∇−−=××−+×+μρρωωρρωρρ (4–64) This form has the desirable feature (from a numerical precision standpoint) of expressing the forcing function due to gravity and the centrifugal acceleration in terms of density differences. For convenience, the relative pressure output is that measured in the stationary global coordinate system. That is, the rotational terms are subtracted from the pressure calculated by the algorithm. Conversely, the total pressure is output in terms of the rotating coordinate system frame. This is done for the convenience of those working in turbomachinery applications. 45
- 59. Chapter 5 Results and Discussions
- 60. Results & Discussion Chapter 5 In order to obtain the performance characteristics of equiangular annular diffuser, the geometric parameters of equiangular annular diffuser is calculated at different area ratios- 2, 3, 4 and 5 and for different angles – 10º, 15º, 20º and 25º. The data are obtained with respect to three sets of velocity 50, 100 and 150 m/s. It is assumed that the flow is exhausted to atmosphere, so pressure at exit of diffuser is assumed to be atmospheric. All the performance parameters are carried out for the non swirl condition. Fig 2 -22 show the results generated by FLOTRAN. In these figure the fluid characteristics like velocity, pressure are shown by different color. A particular color does not give single value of these characteristics, but show the range of these values. If the value of a characteristic at a particular point falls in this range, there will be color of that range. The upper figures show the velocity variation of the fluid at different points in diffuser. The velocity at these points is shown by different colors. In the early part of diffuser section, the velocity at a particular cross section is almost uniform but as flow proceeds, the boundary layers at hub and casing wall grow in size, so at the exit cross section of the diffuser there is large change in velocity. At the mid of section, velocity is large than the velocity at end regions. In the velocity diagram there is a region, which is shown by gray colour. It is the region where velocity is grater than the velocity applied at the inlet section. This increase in velocity is due to convergent effect at the inlet portion of the diffuser which is explained in following paragraph of pressure distribution. It is also observed that for a particular geometry, the velocity variation at different point of diffuser follows the same pattern. In the vector plot of velocity, the direction and magnitude of velocity of fluid particles is shown at different points. It is observed that there is no negative value of fluid velocity at any point, which indicates that there is no reverse flow or the separation at casing wall or recirculation zone near the hub wall, even at divergence angle of 25º. The third figure shows the pressure distribution within the diffuser at different location with the help of different colour, the second figure shows the vector plot of velocity of fluid particle at different point in diffuser. Due to the change of kinetic energy into pressure energy there is continuous reduction in the magnitude of velocity from inlet to ________________________________________________________________________ 47
- 61. Results & Discussion Chapter 5 outlet. It is observed that there is continuous increase in pressure as fluid flow through the diffuser except at the inlet section of diffuser. At the inlet section of diffuser, the substantial change in the pressure across the section is observed; this is because of sudden rise in pressure near the hub and sudden decrease in pressure near casing wall. Because of this the pressure is decreasing instead of increasing along the hub wall upto some distance from inlet. The reason for this entrance loss is that when the flow reaches at the inlet of diffuser, it is turned along the diffuser hub wall, as a result convergence effect is obtained, because of this effect the velocity increases and pressure decreases upto some distance opposite to diffusion process. After the stabilization of flow regime, there is continuous increase in pressure due to diffusion process. The static pressure distribution along the hub and casing wall are shown in figure 23 - 36 at different values of Reynolds No. (at different velocity). Except at the entrance region, there is continuous growth of pressure along the hub and casing wall, this indicates that there is no separation nearby the casing wall or recirculation zone nearby the hub wall. It is observed that for particular geometry i.e. a particular area ratio and divergence angle, the hub and casing wall static pressure distribution follow the same pattern whether the inlet velocity is changing or not. From the figures, it is observed that pressure at hub wall is less than the casing wall. As the flow passes through the diffuser it glides along the casing wall therefore the casing wall behaves as pressure side and hub wall behaves as suction side, so pressure at casing side is more. As the value of Reynolds No. increases, the difference in the pressure at hub and casing wall, at the inlet section, increases; therefore value of entrance losses increases. But the value of overall losses reduces with increase in Reynolds number which can be also shown in the table 3 of pressure loss coefficient. In the present study, the pressure loss coefficient is given by the difference in ideal pressure recovery and the actual static pressure recovery. For a particular area ratio, the value of ideal pressure recovery remains constant, since it depends only on the area ratio. But the actual static pressure recovery continuously increases with increase in the inlet velocity due to higher diffusion. From table 2, it found that for a given geometry there is an increase in Cp with increase in velocity but the increase in the Cp is almost negligible. The reason is that when velocity ________________________________________________________________________ 48
- 62. Results & Discussion Chapter 5 increases, the entrance loss also increases, which surpasses the pressure rise due to increase in velocity. In fig 36 – 43, the graphs are plotted for the values of Cp along the hub and casing wall. These graphs follow the same trend as the static pressure distribution graphs. Near the entrance region, the value of Cp is negative for the casing wall due to entrance static pressure disturbance. As the value of divergence angle increases, this negative value of Cp at hub wall also increases. In fig 44 – 55, the variation of Mach No at the exit section of is plotted. In present study the value of Mach No varies from 0.15 to 0.46. The graphs 44 - 49 are plotted for constant value of divergence angle and Reynolds No. There is large change in Mach No, at section for the lower area ratio. For higher value of AR, curve is flat. With increases in Reynolds No, the curve also becomes flat. At a constant value of Reynolds No, the maximum value of Mach No remains almost constant for a particular AR, whether cone angle changes or not. It is also absorbed that as the value of AR increases, the point of maximum Mach No moves toward the y- axis i.e. toward the hub side. It is found that in this range of Mach No., there is small change in press recovery upto cone angle of 15º. With further increases in angle, it reduces due to high divergence of passage. For the large area ratio and large angle of divergence, FLOTRAN doesn’t give solution, since in there is large disturbance in flow regime. To find out solution in this case a large pipe of constant diameter should be attached to exit portion of diffuser to stabilize the flow regime. But in this situation, the flow condition may be different from the actual condition, so solution are not find out at these conditions. ________________________________________________________________________ 49
- 63. Chapter 6 Conclusions and Future Scope of Work
- 64. Conclusions and Future scope of work Chapter6 6.1 Conclusions Subsonic turbulent flows inside the various diffusers of different geometric are analyzed using the FLOTRAN. On the basis of these studies the following conclusions can be made. 1. The pressure recovery with in the diffuser increases as the flow proceeds; the rate of increase reduces with an increases in the distance from the inlet. 2. For no swirl condition, there is no separation observed at the casing wall even at the cone angle of 25º. 3. With increases in inlet velocity, there is a marginal increase in pressure recovery, since the entrance losses increases with velocity. 4. For the small value of Mach No., there is small change in press recovery upto cone angle of 15º. With further increases in angle, it reduces at high rate due to high divergence of passage. 5. The static pressure distribution increases uniformly along the length of diffuser for both hub and casing walls, since there is no separation or recirculation on the walls. 6. With increase in area ratio pressure recovery increases due to higher rate of diffusion but pressure recovery loss also increases. ___________________________________________________________________________ 51
- 65. Conclusions and Future scope of work Chapter6 6.2 Future scope of work 1. Systematic tests are required with a Varity of diffusers to determine which parameters influence the flow behavior in the annular diffusers. Additional tests with more geometric parameters will give more precise results about flow behavior. 2. As the area ratio and angle of divergence are the important parameters, which indicate the overall diffusion and hence further studies can be extended by varying these parameters. 3. Uniform inlet velocity profile is considered at the inlet of the diffuser. But in many practical situations the flow is nonuniform. Hence the inlet velocity profiles constitute the area of great interest for further studies. 4. Effects of inlet aerodynamic blockage should be included for future study. 5. Inlet swirl parameter also influence the performance of diffuser, hence the swirl conditions must be included for further investigation. 6. Boundary layer phenomenon adversely affects the diffusion process. Suction, blowing and injection of boundary layer can reduce the flow separation at diffuser walls. These effects can be included for further studies. 7. At the inlet section of flow, there is substantial change of pressure across the section. So different inlet parameters like wall curvature, struts etc. should be included for investigation. ___________________________________________________________________________ 52
- 66. REFERENCES 1. Ackert J., 1967. “Aspect of Internal Flow”. Fluid Mechanics of Internal Flow, Ed. Sovran G., Elsevier Amsterdum, pp1. 2. Adkins R.C., Jacobsen O.H., Chevalier P., 1983. “A Premilary Study of Annular Diffuser with Constant Diameter Outer Wall”. ASME Paper No. 83-GT-218. 3. Adkins R.C., 1983. “A simple Method for Design Optimum Annular Diffusers”. ASME Paper No. 83-GT-42. 4. Awai T., Nakagawa T., Sakai T., 1986. “Study of Axially Curved Mixed Flow Vane less Diffuser”. Bull JSME 29, 1759-1764. 5. Cockrell D.J., Markland E., 1963. “A Review of Incompressible Diffuser Flow”. Aircraft Engg. Volume 35, pp 286. 6. Coladipietro R., Schneider J. M., Sridhar K., 1974. “Effects of Inlet Flow Conditions on the Performance of Equiangular Annular Diffusers”. Trans. CSME 3 (2), pp 75-82. 7. Dovzhik S. A., Kartavenko V. M., 1975. “Measurement of the Effect of Flow Swirl on the Efficiency of Annular Ducts and exhaust Nozzles of Axial Turbomachines”. Fluid Mechanics/Soviet Research 4(4), 156-172. 8. Goebel J. H., Japikse D., 1981. “The Performance of an Annular Diffuser Subject to Various Inlet Blockage and Rotor Discharge Effects”. Consortium Final Report, Creare TN-325. 9. Hesterman R., Kim S., Ban Khalid A., Witting S., 1995. “Flow Field and Performances Characteristics of Combustor Diffusers: A Basic Study”. Trans. ASME Journal Engineering for Gas Turbine and Power 117, pp 686-694. 10. Hoadley D., 1970. “Three Dimensional Turbulent Boundary Layers in an Annular Diffuser”. Ph.D. Thesis University of Cambridge. 11. Hoadley D., Hughes D.W., 1969. “Swirling Flow in an Annular Diffuser”. University of Cambridge, Department of Engineering, Report CUED/A- Turbo/TR5. ________________________________________________________________________ 53
- 67. 12. Howard J. H. G., Thornton –Trump A. B., Henseler H. J., 1967. “Performance and Flow Regime for Annular Diffusers”. ASME Paper No. 67-WA/FE-21. 13. Ishkawa K., Nakamura I., 1989. “An Experimental Study on the Performance of Mixed Flow Type Conical Wall Annular Diffuser”. ASME FED-69. 14. Japikse D., 1986. “A New Diffuser Mapping Technique – Studies in Component Performance: Part 1”. ASME Paper No. 84-GT-237, Amsterdam. June 1984; also, Journal of Fluids Engineering, Vol. 108, No. 2, pp 148-156. 15. Japikse D., Pampreen R., 1978. “Annular Diffuser Performance for an Automotive Gas Turbine”. ASME Publication 78-GT-147. 16. Japikse D., 1980. “The Influence of Inlet Turbulence on Diffuser Performance”. Concepts ETI, Inc., Design Data Sheet No. 1. 17. Japikse D., 2000. “Performance of Annular Diffusers Subject to Inlet Flow Field Variations and Exit Distortion”. presented at the ISROMAC conference in Honolulu, Hawaii, March 26-30. 18. Johnston I.H., 1953. “Effect of Inlet Conditions on the Flow in Annular Diffusers”. National Gas Turbine Establishment Memo No.167,Cp No.178 19. Johnston J. P., 1959. “Summary of Results of Test on Short Conical Diffuser with Flow Control Inserts”: as of June 1, 1959.Ingersoll – Rand TN No. 71. 20. Juhasz A.J., 1974. “Performance of an Asymmetric Annular Diffuser with Non Diverging Inner Wall Using Suction”. NASA TN -7575. 21. Kamonicek V., Hibs M., 1974. “Results of Experimental and Theoretical Investigation of Annular Diffuser”. CSIRO, Division of Mechanical Egg. 22. Klein A., 1995. “Characteristics of Combustor Diffusers”. Prog .Aerospace Sci. 31: 171-271. 23. Moller E.S, 1965. “Radial Diffuser Using Incompressible Flow between Disks”. ASME Paper No. 65-FE-12. 24. Moller E.S., 1965. “Radial Flow without Swirl between Parallel Disks Having both Supersonic and Subsonic Regions”. ASME Paper No. 65-FE-11. 25. Shaalan M. R. A., Shabaka I. M. M., 1975. “An Experimental Investigation of the Swirling Flow Performance of an Annular Diffuser at Low Speed”. ASME Paper No. 75-WA/FE-17. ________________________________________________________________________ 54
- 68. 26. Sharan V. K., 1972. “Diffuser Performance Co-Relations”. JASI, Volume 24, pp 415. 27. Sovran G., Klomp E.D., 1967. “Experimentally Determined Optimum Geometries for Rectilinear Diffusers with Rectangular, Conical or Annular Cross-Section”. Fluid Dynamics of Internal Flow, Elsevier Publishing Company. 28. Srinath T., 1968. “An Investigation of the Effects of Swirl on the Flow Regimes and Performance of Annular Diffuser with Equal Inner and Outer Cone Angles”. M.A. Science Thesis , University of Waterloo Canada 29. Stafford, W. Wilbur, James T. Higginbotham, 1955. “Investigation of Two Short Annular Diffuser Configurations Utilizing Suction and Injection as Means of Boundary Layer Control”. NACA RM L54K18. 30. Stafford W. Wilbur, James T.H.1957. “Investigation of Short Annular Diffuser Configuration Utilizing Suction as a Means of Boundary Layer Control”. NACA TN-3996 31. Stevens S. J., Williams G. J., 1980. “The Influence of Inlet Conditions on the Performance of Annular Diffuser”. Trans. ASME Journal Fluids Egg. 102,357- 363. 32. Stevens S. J., Williams G. J., 1969. “Performance of Annular Diffusers”. Gas Turbine Collaboration Committee Report No. 299. 33. Stevens S. J., Fry P., 1973. “Measurements of The Boundary Layer Growth in Annular Diffusers”. Journal Aircraft Feb., pp 73-89. 34. Takehira A., et. al., 1977. “An Experimental Study of the Annular Diffusers in Axial-Flow Compressors and Turbines”. Japan Society of Mechanical Engineers, Paper No.39, 1977. 35. Thayer E. B., 1971. “Evaluation of Curved Wall Annular Diffuser”. ASME Paper No.71-WA/FE-35 36. Wood C.C., Henry J. R., 1958. “Effects of Shock Boundary Layer Interaction on the Long and Short Subsonic Annular Diffuser” .NACA RM L58A31. 37. ANSYS 9.0 FLOTRAN user guide. ________________________________________________________________________ 55
- 69. Appendix
- 70. 57 AR DO L10 L15 L20 L25 2 262.5 319.01 209.93 154.55 120.63 3 375.0 638.02 419.86 309.09 241.26 4 487.5 957.03 629.78 463.64 361.89 5 600.0 – 839.71 618.18 – Table: 1 Geometric Parameters of Annular Diffuser (Equiangular)
- 71. 10º 15º 20º 25º Velocity (m/s.) Velocity (m/s.) Velocity (m/s.) Velocity (m/s.) A N G L E AR 50 100 150 50 100 150 50 100 150 50 100 150 2 0.621 0.625 .646 0.602 0.613 0.629 0.568 0.575 0.579 0.492 0.502 0.496 3 0.748 0.756 0.762 0.731 0.736 0.745 0.682 0.692 0.695 0.619 0.606 0.618 4 0.774 0.784 0.789 0.758 0.766 0.770 0.716 0.772 0.725 0.656 0.657 0.651 5 – – – 0.760 0.769 0.772 0.715 0.722 0.725 – – – Table: 2 Static Pressure Recovery Coefficient For Annular Diffuser ( Equiangular )
- 72. 10º 15º 20º 25º Velocity (m/s.) Velocity (m/s.) Velocity (m/s.) Velocity (m/s.) A N G L E AR 50 100 150 50 100 150 50 100 150 50 100 150 2 0.129 0.125 0.104 0.148 0.137 0.121 0.182 0.175 0.171 0.258 0.248 0.254 3 0.140 0.133 0.127 0.158 0.153 0.144 0.206 0.197 0.194 0.270 0.283 0.271 4 0.164 0.154 0.149 0.180 0.172 0.168 0.222 0.216 0.213 0.282 0.281 0.287 5 – – – 0.200 0.191 0.188 0.245 0.238 0.235 – – – Table: 3 Pressure - Loss Coefficient For Annular Diffuser ( Equiangular )
- 73. Fig -1 Annular Diffuser Performance Chart, B1≅.02 (Sovran and Klomp,1967) 61
- 74. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 2 Diffuser (AR = 2, Angle =10º, Velocity = 50,100 m/s.) 62
- 75. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 3 Diffuser (AR = 2; Angle =10º, Velocity = 150 m/s.; Angle = 15º, Velocity = 50 m/s.) 63
- 76. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 4 Diffuser (AR = 2, Angle =15º, Velocity = 100,150 m/s.) 64
- 77. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 5 Diffuser (AR = 2, Angle = 20º, Velocity = 50,100 m/s.) 65
- 78. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 6 Diffuser (AR = 2; Angle = 20º, Velocity = 150 m/s.; Angle = 25º, Velocity = 50 m/s.) 66
- 79. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 7 Diffuser (AR = 2, Angle = 25º, Velocity = 100,150 m/s.) 67
- 80. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 14 Diffuser (AR = 4, Angle =10º, Velocity = 50,100 m/s.) 74
- 81. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 15 Diffuser (AR = 4; Angle =10º, Velocity = 150 m/s.; Angle = 15º, Velocity = 50 m/s.) 75
- 82. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 16 Diffuser (AR = 4, Angle =15º, Velocity = 100,150 m/s.) 76
- 83. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig -17 Diffuser (AR = 4, Angle = 20º, Velocity = 50,100 m/s.) 77
- 84. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 18 Diffuser (AR = 4; Angle =20º, Velocity = 150 m/s.; Angle = 25º, Velocity = 50 m/s.) 78
- 85. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 19 Diffuser (AR = 4, Angle = 25º, Velocity = 100,150 m/s.) 79
- 86. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 20 Diffuser (AR = 5, Angle =15º, Velocity = 50,100 m/s.) 80
- 87. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 21 Diffuser (AR = 5; Angle =15º, Velocity = 150 m/s.; Angle = 20º, Velocity = 50 m/s.) 81
- 88. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 22 Diffuser (AR = 5, Angle = 20º, Velocity = 100,150 m/s.) 82
- 89. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 8 Diffuser (AR = 3, Angle =10º, Velocity = 50,100 m/s.) 68
- 90. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 9 Diffuser (AR = 3; Angle =10º, Velocity = 150 m/s.; Angle = 15º, Velocity = 50 m/s.) 69
- 91. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 10 Diffuser (AR = 3, Angle =15º, Velocity = 100,150 m/s.) 70
- 92. ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 11 Diffuser (AR = 3, Angle =20º, Velocity = 50,100 m/s.)
- 93. 71 ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig - 12 Diffuser (AR = 3; Angle = 20º, Velocity = 150 m/s.; Angle = 25º, Velocity = 50 m/s.)
- 94. 72 ( Velocity Diagram ) (Vector Plot of Velocity) ( Pressure Diagram ) Fig -13 Diffuser (AR = 3, Angle =25º, Velocity = 100,150 m/s.) 73
- 95. 100000100250100500100750101000101250101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 96000970009800099000100000101000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 890009100093000950009700099000101000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 23 Static Pressure at Hub & Casing-wall (AR = 2, Angle = 10º) 83
- 96. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 9500096000970009800099000100000101000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 99700100200100700101200 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 24 Static Pressure at Hub & Casing-wall (AR = 2, Angle = 15º) 84
- 97. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 96000970009800099000100000101000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 880009000092000940009600098000100000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 25 Static Pressure at Hub & Casing-wall (AR = 3, Angle = 10º) 85
- 98. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 945009550096500975009850099500100500101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 86500885009050092500945009650098500100500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 26 Static Pressure at Hub & Casing-wall (AR = 3, Angle = 15º) 86
- 99. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 940009500096000970009800099000100000101000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 8500087000890009100093000950009700099000101000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 27 Static Pressure at Hub & Casing-wall (AR = 3, Angle = 20º) 87
- 100. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 94000955009700098500100000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 84000865008900091500940009650099000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 28 Static Pressure at Hub & Casing-wall (AR = 3, Angle = 25º) 88
- 101. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 940009500096000970009800099000100000101000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 85500870008850090000915009300094500960009750099000100500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 29 Static Pressure at Hub & Casing-wall (AR = 2, Angle = 20º) 89
- 102. 9900099500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 9300094500960009750099000100500102000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 84000865008900091500940009650099000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 30 Static Pressure at Hub & Casing-wall (AR = 2, Angle = 25º) 90
- 103. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 95000965009800099500101000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 8800090500930009550098000100500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 31 Static Pressure at Hub & Casing-wall (AR = 4, Angle = 10º) 91
- 104. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 945009550096500975009850099500100500101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 865008900091500940009650099000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 32 Static Pressure at Hub & Casing-wall (AR = 4, Angle = 15º) 92
- 105. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 94000955009700098500100000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 855008800090500930009550098000100500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 33 Static Pressure at Hub & Casing-wall (AR = 4, Angle = 20º) 93
- 106. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 94000955009700098500100000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 850008750090000925009500097500100000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 34 Static Pressure at Hub & Casing-wall (AR = 4, Angle = 25º) 94
- 107. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 945009550096500975009850099500100500101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 87000890009100093000950009700099000101000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 35 Static Pressure at Hub & Casing-wall (AR = 5, Angle = 15º) 95
- 108. 99500100000100500101000101500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 2.58×105 ) 94500960009750099000100500 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 5.15×105 ) 860008850091000935009600098500101000 00.10.20.30.40.50.60.70.80.91 X/L Static Pressure (pa) Hub-wallCasing-wall ( Re No.= 7.73×105 ) Fig - 36 Static Pressure at Hub & Casing-wall (AR = 5, Angle = 20º) 96
- 109. -0.100.10.20.30.40.50.600.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 10º -0.25-0.15-0.050.050.150.250.350.450.550.6500.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 15º Fig - 37 Pressure Recovery Coefficient (AR = 2, Re No.= 5.15 ×105 ) 97
- 110. -0.45-0.35-0.25-0.15-0.050.050.150.250.350.450.5500.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 20º -0.65-0.55-0.45-0.35-0.25-0.15-0.050.050.150.250.350.450.5500.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 25º Fig - 38 Pressure Recovery Coefficient (AR = 2, Re No.= 5.15×105 ) 98
- 111. 00.10.20.30.40.50.60.70.800.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 10º -0.100.10.20.30.40.50.60.70.800.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 15º Fig - 39 Pressure Recovery Coefficient (AR = 3, Re No.= 5.15×105 ) 99
- 112. -0.25-0.15-0.050.050.150.250.350.450.550.6500.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 20º -0.4-0.3-0.2-0.100.10.20.30.40.50.600.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 25º Fig – 40 Pressure Recovery Coefficient (AR = 3, Re No.= 5.15×105 ) 100
- 113. 00.10.20.30.40.50.60.70.800.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 10º -0.100.10.20.30.40.50.60.70.800.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 15º Fig - 41 Pressure Recovery Coefficient (AR = 4, Re No.= 5.15×105 ) 101
- 114. -0.15-0.050.050.150.250.350.450.550.650.7500.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 20º -0.25-0.15-0.050.050.150.250.350.450.550.6500.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 25º Fig - 42 Pressure Recovery Coefficient (AR = 4, Re No.= 5.15×105 ) 102
- 115. 00.10.20.30.40.50.60.70.800.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 15º -0.100.10.20.30.40.50.60.700.10.20.30.40.50.60.70.80.91Y/RCpHubTip Angle = 20º Fig - 43 Pressure Recovery Coefficient (AR = 5, Re No.= 5.15×105 ) 103
- 116. 0.050.070.090.110.130.150.1700.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4 Angle = 10º 0.050.070.090.110.130.150.1700.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4AR=5 Angle = 15º Fig - 44 MACH No. at Diffuser Exit (Re No.= 5.15×105 ) 104
- 117. 0.040.060.080.10.120.140.160.1800.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4AR=5 Angle = 20º 0.040.060.080.10.120.140.160.180.20.2200.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4 Angle = 25º Fig - 45 MACH No. at Diffuser Exit (Re No.= 5.15×105 ) 105
- 118. 0.030.040.050.060.070.080.0900.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4 Angle = 10º 0.020.030.040.050.060.070.080.090.100.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4AR=5 Angle = 15º Fig - 46 MACH No. at Diffuser Exit (Re No.= 2.58×105 ) 106
- 119. 0.020.030.040.050.060.070.080.090.100.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4AR=5 Angle = 20º 0.030.040.050.060.070.080.090.10.1100.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4 Angle = 25º Fig - 47 MACH No. at Diffuser Exit (Re No.= 2.58×105 ) 107
- 120. 0.080.10.120.140.160.180.20.220.2400.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4 Angle = 10 0.060.080.10.120.140.160.180.20.220.2400.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4AR=5 Angle = 15 Fig - 48 MACH No. at Diffuser Exit (Re No.= 7.73×105 ) 108
- 121. 0.070.090.110.130.150.170.190.210.230.250.2700.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4AR=5 Angle = 20 0.070.0950.120.1450.170.1950.220.2450.270.29500.10.20.30.40.50.60.70.80.9Y/R MACH No. AR=2AR=3AR=4 Angle = 25 Fig - 49 MACH No. at Diffuser Exit (Re No.= 7.73×105 ) 109
- 122. 0.070.090.110.130.150.170.190.2100.10.20.30.40.50.60.70.80.91Y/R MACH No. α = 10º α = 15º α = 20º α = 25º (AR = 2) 0.040.060.080.10.120.140.1600.10.20.30.40.50.60.70.80.91Y/R MACH No. α = 10º α = 15º α = 20º α = 25º (AR = 3) Fig - 50 MACH No. at Diffuser Exit (Re No.= 5.15×105 ) 110
- 123. 0.040.050.060.070.080.090.10.110.1200.10.20.30.40.50.60.70.80.9Y/R MACH No. α = 10º α = 15º α = 20º α = 25º (AR = 4) 0.0450.050.0550.060.0650.070.07500.10.20.30.40.50.60.70.80.91Y/R MACH No. α = 15º α = 20º (AR = 5) Fig - 51 MACH No. at Diffuser Exit ( Re No.= 5.15×105 ) 111
- 124. 0.030.040.050.060.070.080.090.10.1100.10.20.30.40.50.60.70.80.91Y/R MACH No. α = 10º α = 15º α = 20º α = 25º (AR = 2) 0.0250.0350.0450.0550.0650.07500.10.20.30.40.50.60.70.80.91Y/R MACH No. α = 10º α = 15º α = 20º α = 25º (AR = 3) Fig - 52 MACH No. at Diffuser Exit (Re No.= 2.58×105 ) 112
- 125. 0.0250.030.0350.040.0450.0500.10.20.30.40.50.60.70.80.91Y/R MACH No. α = 10º α = 15º α = 20º α = 25º (AR = 4) 0.0220.0240.0260.0280.030.0320.0340.03600.10.20.30.40.50.60.70.80.91Y/R MACH No. α = 15º α = 20º (AR = 5) Fig - 53 MACH No. at Diffuser Exit (Re No.= 2.58×105 ) 113
- 126. 0.10.150.20.250.30.3500.10.20.30.40.50.60.70.80.91Y/R MACH No. α = 10º α = 15º α = 20º α = 25º (AR = 2) 0.080.120.160.20.2400.10.20.30.40.50.60.70.80.91Y/R MACH No. α = 10º α = 15º α = 20º α = 25º (AR = 3) Fig - 54 MACH No. at Diffuser Exit (Re No.= 7.73×105 ) 114
- 127. 0.070.090.110.130.150.1700.10.20.30.40.50.60.70.80.91Y/R MACH No. α = 10º α = 15º α = 20º α = 25º (AR = 4) 0.060.070.080.090.10.1100.10.20.30.40.50.60.70.80.91Y/R MACH No. α = 15º α = 20º (AR = 5) Fig - 55 MACH No. at Diffuser Exit ( Re No.= 7.73×105 ) 115














![Introduction Chapter 1
A diffuser is a device that increases the pressure of a fluid at the expense of its kinetic energy. The cross-section area of diffuser increases in the direction of flow, therefore fluid is decelerated as it flows through it causing a rise in static pressure along the stream. Such a process is known as diffusion. The flow process near the diffuser walls is subjected to greater retardation due to the formation and development of the boundary layer. A study of the parameters governing the development of the boundary layer and their relationship with diffuser performance is, therefore vital in optimizing the design of a diffuser.
Diffusers are extensively used in centrifugal compressors, axial flow compressors, ram jets, combustion chambers, inlet portions of jet engines etc. The energy transfer in these turbomachineries involves the exchange of significant levels of kinetic energy in order to accomplish the intended purpose. As a consequence, very large levels of residual kinetic energy frequently accompany the work input and work extraction processes, sometime as much as 50% of the total energy transferred. A small change in pressure recovery can increases the efficiency significantly. Therefore diffusers are absolutely essential for good turbomachinery performance.
1.1 TYPE OF DIFFUSERS
1.1.1 Axial Diffuser –
In axial diffusers, fluid flows along the axis of diffusers and there is continuous retardation of the flow. Axial diffuser is divided in to the following categories-
• Conical diffuser
• Channel diffuser
• Annular diffuser
The basic geometric parameters for these type of diffusers are as follows:
For conical diffuser-
Nondimensional length, L/W1
Aspect ratio, AS = b/W1
Area ratio, AR = A2/A1 ()θtan211WLAR+=
For channel diffuser- Nondimensional length, L/D1
Area ratio, AR = A2/A1
()[]21tan21θDLAR+= 2](https://image.slidesharecdn.com/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-141118080335-conversion-gate02/85/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-15-320.jpg)





![Literature Review Chapter2
Diffusers are one of the standard challenges in fluid mechanics. The task of a diffuser is to decelerate the flow and to regain total pressure. It is more difficult to arrange for an efficient deceleration of flow than it is to obtain an efficient acceleration. There is a natural tendency in a diffusing process for the flow to break away from the walls of the diverging passage, reverse its direction, and flow back in direction of the pressure gradient. If the divergence is too rapid, this may result in the formation of eddies with consequent transfer of some kinetic energy into internal energy and a reduction in useful pressure rise. A small angle of divergence, however, implies a long diffuser and a high value of skin friction loss. Usually, flow separation in a diffuser is sought to be avoided due to the invoked additional pressure loss. Other than in many strongly separated flows, such as the flow over a backward facing step, the point of flow separation, in diffuser, is not defined by the geometry but entirely by the pressure gradient. Hence, diffuser flows are very sensitive and are difficult to predict with numerical means. Diffusers have been studied extensively in the past, since this is a very common flow configuration. Apart from the characterization of diffusers, these flows are used to study fundamental physics of pressure-driven flow separations.
Historically, annular diffusers have ranked after channel and conical diffusers in terms of interest for research and hence fewer works is available upon which to establish the technology base for design and performance evaluation. Although annular diffusers are used in gas turbines and turbomachinery installations, it is only in the last decade that there have been any systematic investigations of there performance characteristics. The most notable contribution is that due to Sovran and Klomp [27] who tested over one hundred different geometries, nearly all of which had conically diverging center bodies with an inlet radius ratio (Ri/Ro) of 0.55 to 0.70. The tests were carried out with a thin inlet boundary layer and the diffusers have free discharge. The tests were present as contours of pressure recovery plotted against area ratio and non-dimensional length. Howard et al [12] also tested symmetrical annular diffusers with center bodies of uniform diameter, using fully developed flow at inlet. The limits of the various flow regimes and the optimum performance lines were established. Besides it, some other researchers also contributed in the field of annular diffuser and concluded various important results. Much of the extent data covering the annular diffusers was done in the experimental laboratory to uncover some of the unusual performance characteristics of annular diffusers. But there are still some important unresolved questions. The reason for it is that the numbers of 8](https://image.slidesharecdn.com/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-141118080335-conversion-gate02/85/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-21-320.jpg)
![Literature Review Chapter2
independent varibals are large for annular diffusers. In the annular diffuser the flow take place between two boundary surfaces which can varies independently.
This chapter involves a systematic study of different geometric and flow parameters which influence the overall and internal performance of annular diffusers. In this regard the available literature has been examined with a view to make comments on the state of the art and to recognize the scope of further research on the subject.
2.1 Effect of Geometric Parameters
In an annular diffuser, a number of different geometric variables can influence the variation of pressure recovery and inlet condition of flow. The basic equations of motion reveal the importance of both geometric and aerodynamic parameters on the ultimate performance of annular diffuser. The specification of a wide variety of geometric parameters is essential before the performance of diffuser is given. In this section, the various geometric parameters and there influence on diffuser performance is reviewed.
2.1.1 Passage Divergence and Length
Area ratio and non-dimension length prescribes the overall diffusion and pressure– gradient respectively, which is the principle factor in boundary layer development. The study by Henry and Wood (1958) [36] is useful to understand the subsonic annular diffuser. Two diffusers with area ratio 2.1 and divergence of 5º and 10º were tested at various Mach number. It found by this study that most of data clusters around a line of constant effectiveness. It is also observed that the inner wall is being starved of fluid. If a higher divergence had been used, then one might anticipate stall on the inner surface. An extensive study is carried out by Kmonicek and Hibs (1974) [21] in which, the pressure loss coefficient is found out on the basis of the work of compression required to meet the static pressure rise, the results are very interesting but difficult to understand due to use of unconventional terminology.
Sovran and Klomp (1967) [27] and Howard et al. (1967) [12] produced the first widely used annular diffuser maps for channel diffusers. Sovran and Klomp [27] conducted a large number of performance measurements which spanned a broad selection of geometric types of diffusers. The map is only a broad representation of the bulk of
9](https://image.slidesharecdn.com/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-141118080335-conversion-gate02/85/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-22-320.jpg)
![Literature Review Chapter2
configurations tested in the vicinity of their best performance areas. The poorer diffusers are not well defined by the map. These maps also show optimal diffuser geometrics under different conditions and two optimum lines are established. The line of Cp* shows the best area ratio for a given length/passage height ratio, and the line of Cp** shows the best length/ passage height ratio for a given area ratio. The same results were find out by Howard et al [12]. The important difference between this and the Sovran and Klomp [27] map was that the latter was made for very low inlet aerodynamic blockage whereas the former study was carried out for fully developed inlet profiles, implying high aerodynamic blockage. Along the line of peak recovery there is fairly good agreement between the two maps but in the region of heavy transitory stall the maps disagree substantially.
Johnston (1959) [19] and Johnston (1953) [18] reported a study of four different annular diffusers. Three of the four agree tolerably well with the basics Sovran and Klomp [27] map, one of them disagree substantially; the case a strong disagreement is probably in stall. Srinath (1968) [28] studied four equiangular annular diffuser with 2θ = 7º, 10º, 15º and 20º respectively. Tests were reported with a variety of L/Δr values. The line of best pressure recovery shown as CP* by Sovran and Klomp [27] was again confirmed, and Srinath’s map is quite similar to that of Howard et al. [12]. Srinath [28] also observed that the existence of a down stream pipe improved the pressure recovery of the diffuser itself.
An extensive study of diffusers which, although annular, begin with a circular cross section was reported by Ishikawa and Nakamura (1989) [13]. The author found that the performance of the diffuser differed significantly depending on whether it is parallel or diverging for L/r1 greater than about 2. When both types have the same non dimensional length and area ratio, the parallel diffuser has the higher CP. The lines of optimum performance are also drawn. The line of CP* shows the best area ratio for a given non dimensional length, and the line of CP** shows the best non dimensional length for a given area ratio. In the case of the latter line, there is no difference between the parallel and diverging diffuser.
Ishikawa and Nakamura (1989)[13] also attempted to compare their results with those of Sovran and Klomp[27] for a conventional annular diffuser for the same wall length and area ratio, their diffuser was superior, but since the inlet conditions were different in the
10](https://image.slidesharecdn.com/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-141118080335-conversion-gate02/85/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-23-320.jpg)
![Literature Review Chapter2
two studies, this conclusion is only tentative. It was also found that the addition of a conical center body improves the performance of simple conical diffusers with appreciable or large stall. The study carried out by Moller (1965) [23], [24], who designed an axial to radial band with the intention of eliminating diffusion in the inlet region, found that the peak pressure recovery for the entire band and radial diffuser sections was 0.88 and 0.82 for the low blockage and high blockage cases, respectively. Cockrell and Markland [5] reported that a variation in the area ratio from 2.5 to 8.0 has a small effect on the loss coefficients of conical diffusers.
2.1.2 Wall Contouring
Several annular diffuser studies have been published in which contoured walls were an essential part of the design problem. Thayer (1971) [35] reported that curved wall diffusers had pressure recovery as high as 0.61 to 0.65 for an area ratio of 2.15. An extensive study by Stevens and Williams [31], [32], reported that for curved wall diffuser, good pressure recovery was found for a loss significantly below the level which would be expected from pressure recovery loss correlation , but pressure recovery values were lower then those which would be expected from the Sovran and Klomp[27] map. Upon careful examination, it was determined that the boundary layers in this diffuser are different from those which would be expected in most diffuser studies. Takehira et al (1977) [34] presented extensive data for a large set of both straight annular diffusers and curved wall diffusers, and determined that the use of strong curvature at the exit of diffuser was not debilitating but did produce a penalty compared to noncurved diffusers or diffusers with curvature at the inlet.
An additional study by Japikse [14], [17], shows that wall contouring is an important parameter regarding pressure recovery. Adkins et al (1983) [2], [3], tested an annular diffuser of constant outer radius and a conical center body with cones of different angles. In general the pressure recovery increases with decreasing cone angle for various area ratios, but the 132º and sometimes the 45º cone angle produced lower pressure recoveries than an equivalent sudden expansion. This was attributed to a large and rapid separation at the base of the cone where the diffuser starts. Adding a radius to the base of the cone so that it smoothly blended into the upstream hub, was found to improve the performance.
11](https://image.slidesharecdn.com/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-141118080335-conversion-gate02/85/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-24-320.jpg)
![Literature Review Chapter2
2.2 Effects of Flow Parameters
2.2.1 Aerodynamic Blockage
The aerodynamic blockage on annular diffusers is much less well understood than it is in channel and conical diffusers. Coladipietro et al (1974) [6] reported that for short diffusers, the variation of pressure recovery with blockage was similar to the channel and conical diffusers; that is the pressure recovery decreased with increasing blockage. However, for the long diffusers, higher performance was observed at the higher blockage levels.
Stevens and Williams (1980) [31] determined that pressure recovery initially decreases with increased blockage but then for very long inlet lengths where the flow is able to achieve a fully developed form, the pressure recovery again rises. From a careful study of these data it is evident that not only the inlet boundary layer displacement thickness but also other higher order effects such as turbulence intensity and boundary layer mixing phenomena can greatly alter the measured result. In another study by Geobel and Japikse (1981) [8] found that the pressure recovery reduces as aerodynamic blockage increases. In concluding this section several notes can be made. First, the influence of inlet conditions on annular diffuser performance is more complicated than for channel and conical diffuser. In this case, both the hub and casing surfaces can develop boundary layers with significantly different histories. The two differing boundary layers will experience different growth processes as they pass through the diffuser. Furthermore, blockage on one wall has the effect of modifying the effective flow area and hence the core flow velocity, thereby influencing the growth of the boundary layer on the opposite wall. Hence complex interactions can develop within the diffuser.
2.2.2 Inlet Swirl
The method of swirl generation can itself influence the performance of an annular diffuser and, therefore, consideration must be given first to this question. Most investigators have chosen to generate swirled in a radial inflow plane in order to take advantage of the simple cascade design geometry. Others have preferred to use axial cascade which have the advantage that they more closely simulate specific turbomachinery flow condition and permit control of the spacing between the diffuser and
12](https://image.slidesharecdn.com/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-141118080335-conversion-gate02/85/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-25-320.jpg)
![Literature Review Chapter2
the vanes in form that may be more typical of an actual turbo machine. On the other hand axial cascade invariably introduces tip and hub leakage since the cascades are of a variable geometry type, an effective sealing is impossible. In addition to inlet swirl, there may be changes in inlet turbulence intensity, velocity or total pressure gradients, vorticity or wake shading, and inlet aerodynamic blockage may change indirectly as a function of the swirl angle as it is varied. In order for firm conclusion to be drawn, the effect of swirl variation must be deciphered from the performance data.
Srinath (1968) [28] considered an axial flow equiangular diffuser with swirl between 0º and 15º. Peak pressure recovery was found at approximately 10º and then decreased rapidly. Hoadley and Hughes (1969) [11] tested an annular diffuser with a cylindrical inner body and reported that best recovery was achieved at approximately 10º of swirl. Dovzhik and Kartavenko (1975) [7] also reported by the same type of study that the best performance can be achieved between the range of 10º to 20º of inlet swirl angle. A study is presented by Japikse and Pamprreen (1979) [15]of an exhaust diffuser and hood found that substantial recovery has been achieved even up to swirl angle in excess of 40º.
2.2.3 Inlet Turbulence
With long approach pipes diffuser performance rises as approach length increases. This was first noted in the Cockrell and Markland [5] and attributed this to changes in turbulence which enhances mixing transverse to flow directions, thus reducing the distortions. Indeed, the core turbulence intensity of developing pipe flow rises significantly from La /D is equal to 20 to 45 and than remains nearly constant. Two studies have been published which considered variation in inlet turbulence intensity or structure for there impact on annular diffuser performance. The data of Coladieiepro et al (1974) [6] have included both low and high inlet turbulence intensity levels, and this may be explanation for the unusual measurements observed at different blockage. The second study is the work of Williams and Stevens (1969) [32] and Stevens and Fry (1973) [33] , which showed that substantial improvements in radial momentum transport were achieved by turbulence producing grids and wall spoilers. Additional results by Hestermann et al (1995) [9], and Klein (1995) [22] also show that increasing the level of turbulence to 6 – 8.5 % is beneficial in increasing the pressure recovery and, in one case of removing the separation of stalled diffuser. The conclusion of above study is that the effect of increasing inlet turbulence intensity is to increase pressure recovery.
13](https://image.slidesharecdn.com/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-141118080335-conversion-gate02/85/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-26-320.jpg)
![Literature Review Chapter2
2.2.4 Mach Number Influence
Most annular diffuser research has been carried out at low inlet mach numbers. However, several studies have shown measurement at different Mach number. The study by Thayer (1971) [35], Wood and Henry (1958) [36] and Japikse and Pampreen (1979) [15] illustrate virtual independence of recovery with Mach number up to some critical level of approximately 0.80 to 1.1. The actual level depends on method of measurement and the type of inlet. Wood and Henry [36] show that a shock structure must be presented before the performance begins to deteriorate, but the reference Mach number may have little to do with the actual shock location and shock structure. In most cases, the reduction of performance with Mach number is very slight but in a few cases there can be a degradation of five or ten point of performance recovery.
2.2.5 Reynolds Number Influence
Viscosity is an important parameter in any fluid dynamic process and normally appears in the form of a Reynolds number. Typically, diffusers are characterized by a Reynolds number based on an inlet hydraulic diameter. All studies reported that the Reynolds number is a comparatively weak parameter as long as the flow is in the fully turbulent regime. Crockrell and Markland (1963)[5] state that a variation of the inlet Reynolds number has no significant effect on the diffuser performance if this variation is uncoupled from its effects on the inlet boundary layer parameters. For Reynolds number variation within the range of 2×104–7×105, they also pointed out that the diffuser performance would be practically independent of Reynolds number provided the inlet boundary parameters remain constant. Sharan (1972) [26] reported that for thick boundary layers, there is no change in pressure recovery as the Reynolds number increases.
2.3 Boundary Layer Parameter
The flow in diffuser is governed by the behavior of the boundary layers at the diffuser walls. The deceleration of the flow through the diffuser produces a pressure rise in the stream wise direction. The wall shear layers are therefore subjected to a positive or adverse pressure gradient. As is well known, an adverse pressure gradients cause the wall boundary layers to thicken and possibly separate from the diffuser walls, forming areas of backflow in the diffuser. The net result of thinking of the wall boundary layers or the formation of regions of backflow, is the blockage of flow area which reduces the effective
14](https://image.slidesharecdn.com/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-141118080335-conversion-gate02/85/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-27-320.jpg)
![Literature Review Chapter2
area available to the flow. Reduction in effective flow area in turn results in a reduced pressure rise through the diffuser.
2.3.1 Boundary Layer Suction
The effect of suction consists in the removal of decelerated fluid particles from the boundary layer before they are given a chance to cause separation. Wilbur and Higginbotham (1957) [30], investigated the suction phenomenon and found that a suction flow rate of 2.3% increased the static pressure rise by 25 – 60% and decreased the measured total pressure loss by 63%. In another study by Wilbur and Higginbotham (1955) [29], it is shown that suction control is not efficient when applied in an extensive backflow region such as exists immediately downstream of an abruptly turned body. Experiments by Juhasz (1974) [20], on short annular diffuser showed that the diffuser exit profiles could be shifted either towards the hub or towards the casing of annulus by bleeding off a small fraction of the flow through the inner and outer wall respectively. Boundary Layer Suction is also adopted by Ackert (1967) [1], for both channel and conical diffuser with large divergence angle.
2.3.2 Blowing and Injection
Wilbur and Higginbotham (1955) [29], found that at an injection rate of 3.4%, a 33% increases in the measured static pressure rise and a 50% decrease in the measured total pressure loss can be obtained. Juhasz (1974) [20], have reported results of their investigations on the effect of injecting secondary fluid into wild angle conical diffusers through annular slot at inlet. Injection was found to result in considerable improvement in the uniformity of exit flow as well as in the magnitude of pressure recovery.
15](https://image.slidesharecdn.com/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-141118080335-conversion-gate02/85/48734407-cfd-analysis-of-fluid-flow-through-equiangular-annular-diffuser-28-320.jpg)