4.Sampling and Hilbert Transform
1 like1,904 views
The document discusses sampling and the Hilbert transform. It begins by defining sampling as the reduction of a continuous-time (CT) signal to a discrete-time (DT) signal using a sampler. It describes the Nyquist sampling theorem which specifies the minimum sampling rate to reconstruct the original signal. It then discusses different types of sampling including impulse, natural, and flat top sampling. The document also covers aliasing, the Hilbert transform, and properties and examples of using the Hilbert transform including on bandpass signals and for system representation.
![16
Sampling a CT Signal
Clearly for a finite sample period T, it is not possible to represent every
uncountable, infinite-dimensional continuous-time signal with a
countable, infinite-dimensional discrete-time signal.
In general, an infinite number of CT signals can generate a DT signal.
However, if the signal is band (frequency) limited, and the samples are
sufficiently close, it is possible to uniquely reconstruct the original CT
signal from the sampled signal.
x1(t),
x2(t),
x3(t),
x[n]
t=nT](https://image.slidesharecdn.com/4-190923084231/85/4-Sampling-and-Hilbert-Transform-16-320.jpg)
![The FT of the 1/πt term is –jsgn(ω)
This can be verified by the reciprocity theorem:
if f(t) and F(jω) are transform pairs, then f(jω)
and F(t) are also transform pairs
30
)t(x*
t
1
)t(X)]t(x[H
Hilbert transform
These are
FT
transform
pairs](https://image.slidesharecdn.com/4-190923084231/85/4-Sampling-and-Hilbert-Transform-30-320.jpg)
4.Sampling and Hilbert Transform
- 1. Sampling and Hilbert Transform Prof. Satheesh Monikandan.B INDIAN NAVAL ACADEMY (INDIAN NAVY) EZHIMALA [email protected] 101 INAC-AT19
- 2. Syllabus Contents • Introduction to Signals and Systems • Time-domain Analysis of LTI Systems • Frequency-domain Representations of Signals and Systems • Sampling and Hilbert Transform • Laplace Transform
- 3. Sampling Sampling is the reduction of a CT signal to a DT signal. A sampler is a subsystem or operation that extracts samples from a continuous signal. Sampling theorem specifies the minimum-sampling rate at which a CT signal needs to be uniformly sampled so that the original signal can be completely recovered or reconstructed by these samples alone. Sampling rate must be at least 2fmax, or twice the highest analog frequency component.
- 4. Sampling Nyquist rate is defined as the minimum sampling rate required to represent complete information about continuous signal f(t) in its sampled form, f*(t). Sampling Rate is the number of samples per unit time. Higher the sample frequency obtains a signal which is similar to original analog signal for good audio quality. Statement: A continuous time signal can be represented in its samples and can be recovered back when sampling frequency fs is greater than or equal to the twice the highest frequency component of message signal.
- 5. Sampling
- 6. Sampling
- 7. Types of Sampling Impulse Sampling – Performed by multiplying input signal x(t) with impulse train of period 'T'. – Amplitude of impulse changes with respect to amplitude of input signal x(t). Natural Sampling Flat Top Sampling
- 8. 8 Impulse Train Sampling We need to have a convenient way in which to represent the sampling of a CT signal at regular intervals A common/useful way to do this is through the use of a periodic impulse train signal, p(t), multiplied by the CT signal T is the sampling period s=2 /T is the sampling frequency This is known as impulse train sampling. Note xp(t) is still a continuous time signal n p nTttp tptxtx )()( )()()( T
- 9. Types of Sampling Natural Sampling – Similar to impulse sampling, except the impulse train is replaced by pulse train of period T. – Multiplying input signal x(t) to pulse train.
- 10. Types of Sampling Flat Top / Practical Sampling – During transmission, noise is introduced at top of the transmission pulse which can be easily removed if the pulse is in the form of flat top. – Here, the top of the samples are flat i.e. they have constant amplitude.
- 11. Sampling Theorem ● Processing a signal in digital domain gives several advantages like immunity to temperature drift, accuracy, predictability, ease of design, ease of implementation etc. over analog domain processing. ● Sampling operation samples the incoming signal at regular interval called “Sampling Rate” (Ts ). ● Sampling Rate is determined by Sampling Frequency (Fs ). ● ��=1/�� ● Categories: 1. Baseband Sampling 2. Bandpass Sampling
- 12. Baseband Sampling ● Applicable for LP signals in the baseband (useful frequency components extending from 0Hz to some Fm Hz). ● Theorem: For a faithful reproduction and reconstruction of an analog signal that is confined to a maximum frequency Fm , the signal should be sampled at a Sampling frequency Fs that is greater than or equal to twice the maximum frequency of the signal. ● ≥�� 2�� ● Higher the sampling frequency, higher is the accuracy of representation of the signal. ● Higher sampling frequency implies more samples, which implies more storage space or more memory requirements.
- 13. Baseband Sampling ● In time domain, the process of sampling can be viewed as multiplying the signal with a series of pulses (“pulse train) at regular interval, Ts. ● In frequency domain, the output of the sampling process gives the components of Fm (original frequency content of the signal), Fs±Fm,2Fs±Fm,3Fs±Fm,4Fs±Fm and so on.
- 14. CT Signals by its Samples
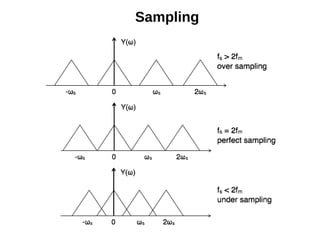
- 16. 16 Sampling a CT Signal Clearly for a finite sample period T, it is not possible to represent every uncountable, infinite-dimensional continuous-time signal with a countable, infinite-dimensional discrete-time signal. In general, an infinite number of CT signals can generate a DT signal. However, if the signal is band (frequency) limited, and the samples are sufficiently close, it is possible to uniquely reconstruct the original CT signal from the sampled signal. x1(t), x2(t), x3(t), x[n] t=nT
- 17. Reconstruction of Signals from its Samples
- 18. Aliasing ● Effect that causes different signals to become indistinguishable (or aliases of one another) when sampled. ● Sampling rate for an analog signal must be at least two times as high as the highest frequency in the analog signal in order to avoid aliasing.
- 19. Types of Aliasing ● Consequence of disobeying the sampling theorem. ● Types: 1. Harmful aliasing that distorts the signal and must be avoided for proper representation of signal in discrete domain. This is when Fs <2B. 2. Useful aliasing that shifts the signal spectral bands up and down for free to our desired frequency through careful system design. This is employed in systems operating at multiple clock rates. 3. Harmless aliasing that is neither good nor bad for the system. This occurs during band-limited pulse shape design to avoid inter-symbol interference (ISI).
- 23. DT Processing of CT Signals
- 25. DT Processing of CT Signals
- 26. Sampling of DT Signals
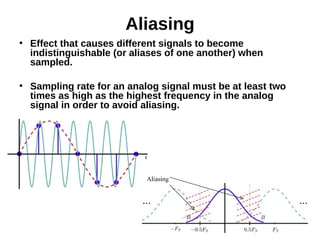
- 30. The FT of the 1/πt term is –jsgn(ω) This can be verified by the reciprocity theorem: if f(t) and F(jω) are transform pairs, then f(jω) and F(t) are also transform pairs 30 )t(x* t 1 )t(X)]t(x[H Hilbert transform These are FT transform pairs
- 31. 31 Hilbert Transform Pairs )tdcos(tAe )tdsin( t Ae x(t) X(t) Special interest in dynamic studies of all kinds of linear systems
- 32. Properties of Hilbert Transform
- 33. 33 PROPERTIES HILBERT TRANSFORM Energy • The energy content of a signal is equal to the energy c ontent of its Hilbert transform Proof • Using Rayleigh's theorem of the Fourier transform, • Using the fact that |-jsgn(f)|2 = 1 except for f = 0, and t he fact that X(f) does not contain any impulses at the origin completes the proof dffXdttxEx 22 )()( dffXdffXfjdttxEx 222 ˆ )()()sgn()(ˆ
- 34. Examples of Hilbert Transform
- 35. Examples of Hilbert Transform
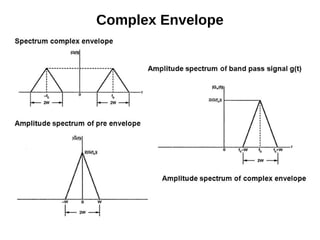
- 36. Pre-envelope
- 37. Pre-envelope
- 39. Complex Envelope
- 40. Real-envelope
- 41. Bandpass Signals
- 42. Bandpass Signals
- 43. Bandpass Signals
- 44. Bandpass Signals
- 45. Bandpass Signals and System Representation