A Tree-Based Definition of Business Process Conformance (Talk @ EDOC 2024)
- 1. A T�ee-Based Defin�ion o� Busines� P�ocess Confo�mance_ A T�ee-Based Defin�ion o� Busines� P�ocess Confo�mance_ Sylvain Hallé Université du Québec à Chicoutimi, Canada September 12th, 2024
- 2. PROLOGUE
- 3. Awards for players Players are eligible for a trophy T if they satisfy a specific condition φT
- 4. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B
- 5. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B hit a minimum of 50 homeruns
- 6. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B HOMERUNS 3 70 hit a minimum of 50 homeruns
- 7. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B HOMERUNS 3 70 hit a minimum of 50 homeruns
- 8. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B HOMERUNS 3 70 hit a minimum of 50 homeruns
- 9. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B hit a minimum of 50 homeruns
- 10. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B hit a minimum of 50 homeruns HOMERUNS 51 70
- 11. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B hit a minimum of 50 homeruns HOMERUNS 51 70
- 12. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B hit a minimum of 50 homeruns HOMERUNS 51 70
- 13. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B won all games or threw a no-hitter
- 14. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B won all games or threw a no-hitter ALL GAMES NO-HITTER
- 15. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B won all games or threw a no-hitter ALL GAMES NO-HITTER
- 16. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B won all games or threw a no-hitter ALL GAMES NO-HITTER
- 17. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B won all games or threw a no-hitter
- 18. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B won all games or threw a no-hitter ALL GAMES NO-HITTER
- 19. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B won all games or threw a no-hitter ALL GAMES NO-HITTER
- 20. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B won all games or threw a no-hitter ALL GAMES NO-HITTER
- 21. Observations
- 22. Observations It is easy to award the trophy when one player satisfies the condition and the other does not
- 23. Observations It is easy to award the trophy when one player satisfies the condition and the other does not Although both players satisfy the condition, one may satisfy it in a "stronger way" numerical condition exceeded by a larger margin "more components" of the condition are satisfied
- 24. Observations It is easy to award the trophy when one player satisfies the condition and the other does not Although both players satisfy the condition, one may satisfy it in a "stronger way" numerical condition exceeded by a larger margin "more components" of the condition are satisfied Sometimes the two players cannot be ranked
- 25. Awards for players Players are eligible for a dunce hat H if they violate a specific condition φH D D D Players are eligible for a trophy T if they satisfy a specific condition φT
- 26. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B
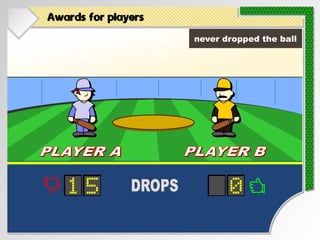
- 27. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B never dropped the ball
- 28. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B never dropped the ball DROPS 15 0
- 29. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B never dropped the ball DROPS 15 0
- 30. Awards for players D D D PLAYER A PLAYER A PLAYER B PLAYER B never dropped the ball DROPS 15 0
- 31. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B never dropped the ball
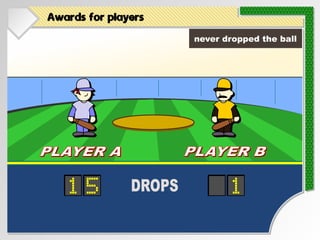
- 32. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B never dropped the ball DROPS 15 1
- 33. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B never dropped the ball DROPS 15 1
- 34. Awards for players D D D PLAYER A PLAYER A PLAYER B PLAYER B never dropped the ball DROPS 15 1
- 35. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B stole at least one base and scored at least one run
- 36. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B stole at least one base and scored at least one run STOLE BASE SCORED RUN
- 37. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B stole at least one base and scored at least one run STOLE BASE SCORED RUN
- 38. Awards for players D D D PLAYER A PLAYER A PLAYER B PLAYER B stole at least one base and scored at least one run STOLE BASE SCORED RUN
- 39. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B stole at least one base and scored at least one run
- 40. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B stole at least one base and scored at least one run STOLE BASE SCORED RUN
- 41. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B stole at least one base and scored at least one run STOLE BASE SCORED RUN
- 42. Awards for players PLAYER A PLAYER A PLAYER B PLAYER B stole at least one base and scored at least one run STOLE BASE SCORED RUN
- 44. Observations (again) It is easy to award the dunce hat when one player violates the condition and the other does not
- 45. Although both players violate the condition, one may violate it in a "stronger way" numerical condition not met by a larger margin more components of the condition are violated Observations (again) It is easy to award the dunce hat when one player violates the condition and the other does not
- 46. Although both players violate the condition, one may violate it in a "stronger way" numerical condition not met by a larger margin more components of the condition are violated Sometimes the two players cannot be ranked Observations (again) It is easy to award the dunce hat when one player violates the condition and the other does not
- 47. Ranking players For a given condition φ, we can define a relation that ranks players D D D "bad" "good"
- 48. Ranking players For a given condition φ, we can define a relation that ranks players D D D "bad" "good"
- 49. Ranking players For a given condition φ, we can define a relation that ranks players D D D "bad" "good"
- 50. Ranking players For a given condition φ, we can define a relation that ranks players D D D "bad" "good"
- 51. One player satisfies the condition and the other does not Ranking players For a given condition φ, we can define a relation that ranks players D D D "bad" "good"
- 52. One player satisfies the condition "in a stronger way" Ranking players For a given condition φ, we can define a relation that ranks players D D D "bad" "good"
- 53. One player violates the condition "in a stronger way" Ranking players For a given condition φ, we can define a relation that ranks players D D D "bad" "good"
- 54. Sometimes the players cannot be ranked Ranking players For a given condition φ, we can define a relation that ranks players D D D "bad" "good"
- 55. Satisfaction false true ⊤ ⊤ ⊥ ⊥ For a given condition φ, satisfaction can be generalized to a partial order
- 56. MAIN PROGRAM
- 57. The execution of a business process generates a sequence of events called a trace σ Business processes Obtain Customer Info Identify Customer Info Retrieve Full Customer Dtl Analyze Customer Relation Select Deposit Service Submit Deposit Prepare Prop. Doc Propose Account Opening Schedule Status Review Open Acc Status Review Verify Customer ID Open Account Record Customer Info Receive customer request Validate Acc Info Close Acc Apply Acc Policy Activate Acc Record Acc Info Evaluate Deposit Val Do Deposit Report Large Deposit Notify Customer Non-VIP VIP
- 58. The execution of a business process generates a sequence of events called a trace σ Business processes a b e c d f g h i j k l m n o q r p s t u v w ¬α α
- 59. The execution of a business process generates a sequence of events called a trace σ Business processes a b e c d f g h i j k l m n o q r p s t u v w ¬α α σ = a b e f i k j m l n o p w
- 60. Each event is modeled as a set of attribute-value pairs. Business processes timestamp action location agent organization duration . . . Possible attributes: a v
- 61. A business process may be subject to a set of conformance constraints, expressed as conditions on a trace: Conformance constraints When n occurs, b and m occurred before If α holds, the process duration when n occurs is at most 7 days At least one of i, n and o is performed by a manager Activity u is immediately preceded by t etc.
- 62. A trace can either satisfy or violate a constraint Conformance constraints
- 63. A trace can either satisfy or violate a constraint Conformance constraints If α holds, the process duration when n occurs is at most 7 days
- 64. A trace can either satisfy or violate a constraint Conformance constraints If α holds, the process duration when n occurs is at most 7 days a b c d e f i j k l m n o p w
- 65. A trace can either satisfy or violate a constraint Conformance constraints If α holds, the process duration when n occurs is at most 7 days a b c d e f i j k l m n o p w = 5 d.
- 66. A trace can either satisfy or violate a constraint Conformance constraints If α holds, the process duration when n occurs is at most 7 days a b c d e f i j k l m n o p w = 5 d.
- 67. A trace can either satisfy or violate a constraint Conformance constraints If α holds, the process duration when n occurs is at most 7 days a b c d e f i j k l m n o p w = 5 d. a b c d e f g h i k j m l n o p w = 8 d.
- 68. Constraints can be formalized as expressions of Linear Temporal Logic* Conformance constraints *including past modalities When n occurs, b and m occurred before If α holds, the process duration when n occurs is at most 7 days At least one of i, n and o is performed by a manager Activity u is immediately preceded by t
- 69. Constraints can be formalized as expressions of Linear Temporal Logic* Conformance constraints *including past modalities H ( = n → (O ( = b) ∧ O ( = m)) If α holds, the process duration when n occurs is at most 7 days At least one of i, n and o is performed by a manager Activity u is immediately preceded by t
- 70. Constraints can be formalized as expressions of Linear Temporal Logic* Conformance constraints *including past modalities H ( = n → (O ( = b) ∧ O ( = m)) α → G ( = n → < 7) At least one of i, n and o is performed by a manager Activity u is immediately preceded by t
- 71. Constraints can be formalized as expressions of Linear Temporal Logic* Conformance constraints *including past modalities H ( = n → (O ( = b) ∧ O ( = m)) α → G ( = n → < 7) F ( = i ∧ = M) F ( = n ∧ = M) ∨ ∨ F ( = o ∧ = M) Activity u is immediately preceded by t
- 72. Constraints can be formalized as expressions of Linear Temporal Logic* Conformance constraints *including past modalities H ( = n → (O ( = b) ∧ O ( = m)) α → G ( = n → < 7) F ( = i ∧ = M) F ( = n ∧ = M) ∨ ∨ F ( = o ∧ = M) H ( = u → (Y ( = t))
- 73. Goal false true ⊤ ⊤ ⊥ ⊥ Generalize the satisfaction relation of LTL to a partial order
- 74. Goal false true ⊤ ⊤ ⊥ ⊥ Generalize the satisfaction relation of LTL to a partial order σ σ σ σ σ σ σ
- 75. Labeled tree A labeled colored tree is a recursive structure of the form: T = ⟨ℓ, [T, ..., T]⟩ | ε node label children ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ A tree node n is also associated with a color c(n) ∈ { , , } ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ
- 76. Evaluation tree From a trace σ and an LTL condition φ, function τ(σ, φ) constructs a labeled tree as follows: τ(σ, p(v1, ..., vn)) ⟨p, [v1, ..., vn]⟩ τ(σ, ¬φ) ⟨¬, [τ(σ, φ)]⟩ τ(σ, X φ) ⟨X, [τ(σ[1..], φ)]⟩ τ(σ, φ1 ∧ ... ∧ φn) ⟨∧, [τ(σ, φ1), ..., τ(σ, φn)]⟩ τ(σ, φ1 ∨ ... ∨ φn) ⟨∨, [τ(σ, φ1), ..., τ(σ, φn)]⟩ τ(σ, G φ) ⟨G, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩ τ(σ, F φ) ⟨F, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩ ⟨O, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩ τ(σ, O φ) τ(σ, Y φ) ⟨Y, [τ(σ[0..|σ| - 2], φ)]⟩ τ(σ, H φ) ⟨H, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩ = = = = = = = = = =
- 77. Evaluation tree From a trace σ and an LTL condition φ, function τ(σ, φ) constructs a labeled tree as follows: τ(σ, p(v1, ..., vn)) ⟨p, [v1, ..., vn]⟩ τ(σ, ¬φ) ⟨¬, [τ(σ, φ)]⟩ τ(σ, X φ) ⟨X, [τ(σ[1..], φ)]⟩ τ(σ, φ1 ∧ ... ∧ φn) ⟨∧, [τ(σ, φ1), ..., τ(σ, φn)]⟩ τ(σ, φ1 ∨ ... ∨ φn) ⟨∨, [τ(σ, φ1), ..., τ(σ, φn)]⟩ τ(σ, G φ) ⟨G, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩ τ(σ, F φ) ⟨F, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩ ⟨O, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩ τ(σ, O φ) τ(σ, Y φ) ⟨Y, [τ(σ[0..|σ| - 2], φ)]⟩ τ(σ, H φ) ⟨H, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩ = = = = = = = = = = suffix of σ starting at index 1
- 78. Evaluation tree From a trace σ and an LTL condition φ, function τ(σ, φ) constructs a labeled tree as follows: τ(σ, p(v1, ..., vn)) ⟨p, [v1, ..., vn]⟩ τ(σ, ¬φ) ⟨¬, [τ(σ, φ)]⟩ τ(σ, X φ) ⟨X, [τ(σ[1..], φ)]⟩ τ(σ, φ1 ∧ ... ∧ φn) ⟨∧, [τ(σ, φ1), ..., τ(σ, φn)]⟩ τ(σ, φ1 ∨ ... ∨ φn) ⟨∨, [τ(σ, φ1), ..., τ(σ, φn)]⟩ τ(σ, G φ) ⟨G, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩ τ(σ, F φ) ⟨F, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩ ⟨O, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩ τ(σ, O φ) τ(σ, Y φ) ⟨Y, [τ(σ[0..|σ| - 2], φ)]⟩ τ(σ, H φ) ⟨H, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩ = = = = = = = = = = length of σ
- 79. Evaluation tree: example Consider the trace of 4 events: σ = {a ↦ 0}, {a ↦ 1}, {a ↦ 1}, {a ↦ 0} and the LTL condition: φ = G (a = 0) Then τ(σ, φ) is:
- 80. Evaluation tree: example Consider the trace of 4 events: σ = {a ↦ 0}, {a ↦ 1}, {a ↦ 1}, {a ↦ 0} and the LTL condition: φ = G (a = 0) Then τ(σ, φ) is: G
- 81. Evaluation tree: example Consider the trace of 4 events: σ = {a ↦ 0}, {a ↦ 1}, {a ↦ 1}, {a ↦ 0} and the LTL condition: φ = G (a = 0) Then τ(σ, φ) is: = 0 a G
- 82. Evaluation tree: example Consider the trace of 4 events: σ = {a ↦ 0}, {a ↦ 1}, {a ↦ 1}, {a ↦ 0} and the LTL condition: φ = G (a = 0) Then τ(σ, φ) is: = 0 a = 0 a G
- 83. Evaluation tree: example Consider the trace of 4 events: σ = {a ↦ 0}, {a ↦ 1}, {a ↦ 1}, {a ↦ 0} and the LTL condition: φ = G (a = 0) Then τ(σ, φ) is: = 0 a = 0 a = 0 a G
- 84. Evaluation tree: example Consider the trace of 4 events: σ = {a ↦ 0}, {a ↦ 1}, {a ↦ 1}, {a ↦ 0} and the LTL condition: φ = G (a = 0) Then τ(σ, φ) is: = 0 a = 0 a = 0 a = 0 a G
- 85. Evaluation tree: example The color of the root of τ(σ, φ) is defined as: c(τ(σ, φ)) = { if σ satisfies φ if σ violates φ otherwise The resulting colored tree is called an evaluation tree.
- 86. Evaluation tree: example Consider the trace of 4 events: σ = {a ↦ 0}, {a ↦ 1}, {a ↦ 1}, {a ↦ 0} and the LTL condition: φ = G (a = 0) Then τ(σ, φ) is: = 0 a = 0 a = 0 a = 0 a G
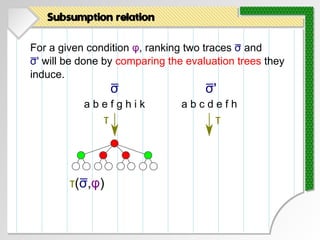
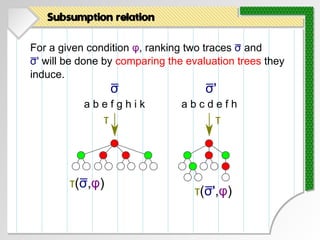
- 87. For a given condition φ, ranking two traces σ and σ' will be done by comparing the evaluation trees they induce. Subsumption relation
- 88. For a given condition φ, ranking two traces σ and σ' will be done by comparing the evaluation trees they induce. Subsumption relation σ a b e f g h i k a b c d e f h σ'
- 89. For a given condition φ, ranking two traces σ and σ' will be done by comparing the evaluation trees they induce. Subsumption relation σ a b e f g h i k a b c d e f h σ' τ
- 90. For a given condition φ, ranking two traces σ and σ' will be done by comparing the evaluation trees they induce. Subsumption relation σ a b e f g h i k a b c d e f h σ' τ τ(σ,φ)
- 91. For a given condition φ, ranking two traces σ and σ' will be done by comparing the evaluation trees they induce. Subsumption relation σ a b e f g h i k a b c d e f h σ' τ τ(σ,φ) τ
- 92. For a given condition φ, ranking two traces σ and σ' will be done by comparing the evaluation trees they induce. Subsumption relation σ a b e f g h i k a b c d e f h σ' τ τ(σ,φ) τ τ(σ',φ)
- 93. For a given condition φ, ranking two traces σ and σ' will be done by comparing the evaluation trees they induce. Subsumption relation σ a b e f g h i k a b c d e f h σ' τ τ(σ,φ) τ τ(σ',φ) vs.
- 94. Subsumption relation . . . T1 . . . T2
- 95. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and...
- 96. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 1 The root of T1 is green T1
- 97. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 1 The root of T1 is green T1 the root of T2 is also green T2
- 98. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 1 The root of T1 is green T1 the root of T2 is also green T2 for every green child T of T1, there exists a distinct child T' of T2 such that T T'
- 99. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 1 The root of T1 is green T1 the root of T2 is also green T2 for every green child T of T1, there exists a distinct child T' of T2 such that T T' T
- 100. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 1 The root of T1 is green T1 the root of T2 is also green T2 for every green child T of T1, there exists a distinct child T' of T2 such that T T' T T'
- 101. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 1 The root of T1 is green T1 the root of T2 is also green T2 for every green child T of T1, there exists a distinct child T' of T2 such that T T' T T' . . . T1 . . . T2 T1 T2 T T'
- 102. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and...
- 103. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 2 The root of T1 is red T1
- 104. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 2 The root of T1 is red T1 the root of T2 is red or green T2
- 105. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 2 The root of T1 is red T1 the root of T2 is red or green T2 for every red child T' of T2, there exists a distinct child T of T1 such that T T'
- 106. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 2 The root of T1 is red T1 the root of T2 is red or green T2 for every red child T' of T2, there exists a distinct child T of T1 such that T T' T'
- 107. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 2 The root of T1 is red T1 the root of T2 is red or green T2 for every red child T' of T2, there exists a distinct child T of T1 such that T T' T' T
- 108. Subsumption relation . . . T1 . . . T2 We say that T1 is subsumed by T2 (noted T1 T2) if their roots have the same label, and... CASE 2 The root of T1 is red T1 the root of T2 is red or green T2 for every red child T' of T2, there exists a distinct child T of T1 such that T T' T' T . . . T1 . . . T2 T1 T T' T2
- 109. Some examples a = 0 ∨ b = 0 ∨ = a 0 = b 0 ∨ = a 0 = b 0 t1 t2 {a ↦ 0, b ↦ 1} {a ↦ 0, b ↦ 0} ⊑
- 110. Some examples a = 0 ∨ b = 0 ∨ = a 0 = b 0 ∨ = a 0 = b 0 t1 t2 {a ↦ 0, b ↦ 1} {a ↦ 0, b ↦ 0} ⊑ t1 t2 ⊑
- 111. Some examples a = 0 ∨ b = 0 ∨ = a 0 = b 0 ∨ = a 0 = b 0 t1 t2 {a ↦ 0, b ↦ 1} {a ↦ 0, b ↦ 0} ⊑ t1 t2 ⊑ Although both players satisfy the condition, one may satisfy it in a "stronger way" "more components" of the condition are satisfied
- 112. Some examples a = 0 ∧ b = 0 ∧ = a 0 = b 0 ∧ = a 0 = b 0 t1 t2 {a ↦ 1, b ↦ 1} {a ↦ 0, b ↦ 1} ⊑
- 113. t1 t2 ⊑ Some examples a = 0 ∧ b = 0 ∧ = a 0 = b 0 ∧ = a 0 = b 0 t1 t2 {a ↦ 1, b ↦ 1} {a ↦ 0, b ↦ 1} ⊑
- 114. t1 t2 ⊑ Some examples a = 0 ∧ b = 0 ∧ = a 0 = b 0 ∧ = a 0 = b 0 t1 t2 {a ↦ 1, b ↦ 1} {a ↦ 0, b ↦ 1} ⊑ "more components" of the condition are violated Although both players violate the condition, one may violate it in a "stronger way" D D D
- 115. Some examples a = 0 ∨ (b = 0 ∧ c = 0) t1 ∨ = a 0 b 0 c 0 ∧ ∨ = a 0 = b 0 c 0 ∧ t2 {a ↦ 1, b ↦ 0, c ↦ 1} {a ↦ 1, b ↦ 1, c ↦ 0} = = =
- 116. Some examples a = 0 ∨ (b = 0 ∧ c = 0) t1 ∨ = a 0 b 0 c 0 ∧ ∨ = a 0 = b 0 c 0 ∧ t2 {a ↦ 1, b ↦ 0, c ↦ 1} {a ↦ 1, b ↦ 1, c ↦ 0} = = = t1 t2 ⊑
- 117. Some examples a = 0 ∨ (b = 0 ∧ c = 0) t1 ∨ = a 0 b 0 c 0 ∧ ∨ = a 0 = b 0 c 0 ∧ t2 {a ↦ 1, b ↦ 0, c ↦ 1} {a ↦ 1, b ↦ 1, c ↦ 0} = = = t1 t2 ⊑ t2 t1 ⊑
- 118. Some examples a = 0 ∨ (b = 0 ∧ c = 0) t1 ∨ = a 0 b 0 c 0 ∧ ∨ = a 0 = b 0 c 0 ∧ t2 {a ↦ 1, b ↦ 0, c ↦ 1} {a ↦ 1, b ↦ 1, c ↦ 0} = = = t1 t2 ⊑ t2 t1 ⊑ Sometimes the players cannot be ranked
- 119. F (a = 0) Some examples ⊑ F = 0 = 0 t2 {a ↦ 0}, {a ↦ 1}, {a ↦ 1}, {a ↦ 0} = 0 = 0 {a ↦ 1}, {a ↦ 0} F = 0 = a a a a a a 0 t1
- 120. t1 t2 ⊑ F (a = 0) Some examples ⊑ F = 0 = 0 t2 {a ↦ 0}, {a ↦ 1}, {a ↦ 1}, {a ↦ 0} = 0 = 0 {a ↦ 1}, {a ↦ 0} F = 0 = a a a a a a 0 t1
- 121. a = 4 Some examples t2 {a ↦ 5} = 4 {a ↦ 2} = 4 a a t1
- 122. a = 4 Some examples t2 {a ↦ 5} = 4 {a ↦ 2} = 4 a a t1 t1 t2 ⊑
- 123. a = 4 Some examples t2 {a ↦ 5} = 4 {a ↦ 2} = 4 a a t1 t1 t2 ⊑ t2 t1 ⊑
- 124. a = 4 Some examples t2 {a ↦ 5} = 4 {a ↦ 2} = 4 a a t1 t1 t2 ⊑ t2 t1 ⊑ 0 1 2 3 4 5 6 7 8
- 125. a = 4 Some examples t2 {a ↦ 5} = 4 {a ↦ 2} = 4 a a t1 t1 t2 ⊑ t2 t1 ⊑ 0 1 2 3 4 5 6 7 8
- 126. Some examples {a ↦ 5} {a ↦ 2} a = 4 0 1 2 3 4 5 6 7 8
- 127. Some examples {a ↦ 5} {a ↦ 2} a = 4 δ(x,y) = |x-y| 0 1 2 3 4 5 6 7 8
- 128. Some examples {a ↦ 5} {a ↦ 2} δ(a,4) ≤ 0 ∧ δ(a,4) ≤ 1 ∧ δ(a,4) ≤ 2 δ(x,y) = |x-y| 0 1 2 3 4 5 6 7 8
- 129. Some examples {a ↦ 5} {a ↦ 2} δ(a,4) ≤ 0 ∧ δ(a,4) ≤ 1 ∧ δ(a,4) ≤ 2 δ(x,y) = |x-y| t2 t1 ∧ 0 ≤ δ a 4 1 ≤ δ a 4 2 ≤ δ a 4 ∧ 0 ≤ δ a 4 1 ≤ δ a 4 2 ≤ δ a 4 0 1 2 3 4 5 6 7 8
- 130. t1 t2 ⊑ Some examples {a ↦ 5} {a ↦ 2} δ(a,4) ≤ 0 ∧ δ(a,4) ≤ 1 ∧ δ(a,4) ≤ 2 δ(x,y) = |x-y| t2 t1 ∧ 0 ≤ δ a 4 1 ≤ δ a 4 2 ≤ δ a 4 ∧ 0 ≤ δ a 4 1 ≤ δ a 4 2 ≤ δ a 4 0 1 2 3 4 5 6 7 8
- 131. t1 t2 ⊑ Some examples {a ↦ 5} {a ↦ 2} δ(a,4) ≤ 0 ∧ δ(a,4) ≤ 1 ∧ δ(a,4) ≤ 2 δ(x,y) = |x-y| t2 t1 ∧ 0 ≤ δ a 4 1 ≤ δ a 4 2 ≤ δ a 4 ∧ 0 ≤ δ a 4 1 ≤ δ a 4 2 ≤ δ a 4 0 1 2 3 4 5 6 7 8 numerical condition not met by a larger margin Although both players violate the condition, one may violate it in a "stronger way" D D D
- 132. Positive points
- 133. Positive points The subsumption relation can compare two executions of a process with respect to an arbitrary* LTL conformance condition *In Negated Normal Form (NNF)
- 134. Positive points The subsumption relation can compare two executions of a process with respect to an arbitrary* LTL conformance condition *In Negated Normal Form (NNF) It does not require any additional information from the user (weights, coefficients, etc.)
- 135. Positive points The subsumption relation can compare two executions of a process with respect to an arbitrary* LTL conformance condition *In Negated Normal Form (NNF) It does not require any additional information from the user (weights, coefficients, etc.) It does not involve any explicit counting or arithmetic calculations
- 136. Positive points The subsumption relation can compare two executions of a process with respect to an arbitrary* LTL conformance condition *In Negated Normal Form (NNF) It does not require any additional information from the user (weights, coefficients, etc.) It does not involve any explicit counting or arithmetic calculations It does not output a numerical value
- 137. Positive points The subsumption relation can compare two executions of a process with respect to an arbitrary* LTL conformance condition *In Negated Normal Form (NNF) It does not require any additional information from the user (weights, coefficients, etc.) It does not involve any explicit counting or arithmetic calculations It does not output a numerical value It produces a ranking mostly matching our intuition
- 138. Positive points The subsumption relation can compare two executions of a process with respect to an arbitrary* LTL conformance condition *In Negated Normal Form (NNF) It does not require any additional information from the user (weights, coefficients, etc.) It does not involve any explicit counting or arithmetic calculations It does not output a numerical value It produces a ranking mostly matching our intuition It is concretely implemented: https://github.com/liflab/shaded-compliance
- 139. Some experimental results Implementation tested on a sample of real-world and synthetic logs and conformance properties
- 140. Challenges
- 141. Challenges Finding a mapping between sub-trees is computationally expensive more compact representation of evaluation trees as DAGs
- 142. Challenges Finding a mapping between sub-trees is computationally expensive more compact representation of evaluation trees as DAGs Subsumption may be excessively fine-grained compare "simplified" versions of evaluation trees instead
- 143. Challenges Finding a mapping between sub-trees is computationally expensive more compact representation of evaluation trees as DAGs Subsumption may be excessively fine-grained compare "simplified" versions of evaluation trees instead It does not directly accommodate user-defined weights accept an order relation between sub-formulas
- 144. Challenges Finding a mapping between sub-trees is computationally expensive more compact representation of evaluation trees as DAGs Subsumption may be excessively fine-grained compare "simplified" versions of evaluation trees instead It does not directly accommodate user-defined weights accept an order relation between sub-formulas How to evaluate incrementally on a stream? incorporate into the library
- 145. Possible uses All executions of a process are arranged into a (finite) lattice 1 1 3 3 3 3 9 9 1 1 3 9 3 3 9 3 number of equivalent traces
- 146. Possible uses The traces of a specific log can be placed on this lattice (a form of visualization) 0 0 0 1 0 0 1 0 6 12 0 0 0 0 5 1
- 147. Possible uses "Layers" of the lattice can formally model service level agreements (SLAs) 1 1 3 3 3 3 9 9 1 1 3 9 3 3 9 3
- 148. The End_ The End_







































































![Labeled tree
A labeled colored tree is a recursive structure of the
form:
T = ⟨ℓ, [T, ..., T]⟩ | ε
node label
children
ℓ
ℓ ℓ
ℓ ℓ ℓ ℓ ℓ
A tree node n is also
associated with a color
c(n) ∈ { , , }
ℓ ℓ ℓ ℓ ℓ ℓ
ℓ ℓ](https://image.slidesharecdn.com/slides-240913090841-8724bb6e/85/A-Tree-Based-Definition-of-Business-Process-Conformance-Talk-EDOC-2024-75-320.jpg)
![Evaluation tree
From a trace σ and an LTL condition φ, function
τ(σ, φ) constructs a labeled tree as follows:
τ(σ, p(v1, ..., vn)) ⟨p, [v1, ..., vn]⟩
τ(σ, ¬φ) ⟨¬, [τ(σ, φ)]⟩
τ(σ, X φ) ⟨X, [τ(σ[1..], φ)]⟩
τ(σ, φ1 ∧ ... ∧ φn) ⟨∧, [τ(σ, φ1), ..., τ(σ, φn)]⟩
τ(σ, φ1 ∨ ... ∨ φn) ⟨∨, [τ(σ, φ1), ..., τ(σ, φn)]⟩
τ(σ, G φ) ⟨G, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩
τ(σ, F φ) ⟨F, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩
⟨O, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩
τ(σ, O φ)
τ(σ, Y φ) ⟨Y, [τ(σ[0..|σ| - 2], φ)]⟩
τ(σ, H φ) ⟨H, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩
=
=
=
=
=
=
=
=
=
=](https://image.slidesharecdn.com/slides-240913090841-8724bb6e/85/A-Tree-Based-Definition-of-Business-Process-Conformance-Talk-EDOC-2024-76-320.jpg)
![Evaluation tree
From a trace σ and an LTL condition φ, function
τ(σ, φ) constructs a labeled tree as follows:
τ(σ, p(v1, ..., vn)) ⟨p, [v1, ..., vn]⟩
τ(σ, ¬φ) ⟨¬, [τ(σ, φ)]⟩
τ(σ, X φ) ⟨X, [τ(σ[1..], φ)]⟩
τ(σ, φ1 ∧ ... ∧ φn) ⟨∧, [τ(σ, φ1), ..., τ(σ, φn)]⟩
τ(σ, φ1 ∨ ... ∨ φn) ⟨∨, [τ(σ, φ1), ..., τ(σ, φn)]⟩
τ(σ, G φ) ⟨G, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩
τ(σ, F φ) ⟨F, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩
⟨O, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩
τ(σ, O φ)
τ(σ, Y φ) ⟨Y, [τ(σ[0..|σ| - 2], φ)]⟩
τ(σ, H φ) ⟨H, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩
=
=
=
=
=
=
=
=
=
=
suffix of σ starting
at index 1](https://image.slidesharecdn.com/slides-240913090841-8724bb6e/85/A-Tree-Based-Definition-of-Business-Process-Conformance-Talk-EDOC-2024-77-320.jpg)
![Evaluation tree
From a trace σ and an LTL condition φ, function
τ(σ, φ) constructs a labeled tree as follows:
τ(σ, p(v1, ..., vn)) ⟨p, [v1, ..., vn]⟩
τ(σ, ¬φ) ⟨¬, [τ(σ, φ)]⟩
τ(σ, X φ) ⟨X, [τ(σ[1..], φ)]⟩
τ(σ, φ1 ∧ ... ∧ φn) ⟨∧, [τ(σ, φ1), ..., τ(σ, φn)]⟩
τ(σ, φ1 ∨ ... ∨ φn) ⟨∨, [τ(σ, φ1), ..., τ(σ, φn)]⟩
τ(σ, G φ) ⟨G, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩
τ(σ, F φ) ⟨F, [τ(σ[0..], φ), τ(σ[1..], φ), ..., τ(σ[|σ| - 1], φ)]⟩
⟨O, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩
τ(σ, O φ)
τ(σ, Y φ) ⟨Y, [τ(σ[0..|σ| - 2], φ)]⟩
τ(σ, H φ) ⟨H, [τ(σ[0..|σ| - 2], φ), τ(σ[|σ| - 3], φ), ..., τ(σ[0], φ)]⟩
=
=
=
=
=
=
=
=
=
=
length of σ](https://image.slidesharecdn.com/slides-240913090841-8724bb6e/85/A-Tree-Based-Definition-of-Business-Process-Conformance-Talk-EDOC-2024-78-320.jpg)