Algorithm analysis insertion sort and asymptotic notations
- 1. Algorithms Dr. AMIT KUMAR @JUET
- 2. Introduction • The methods of algorithm design form one of the core practical technologies of computer science. • The main aim of this lecture is to familiarize the student with the framework we shall use through the course about the design and analysis of algorithms. • We start with a discussion of the algorithms needed to solve computational problems. The problem of sorting is used as a running example. • We introduce a pseudocode to show how we shall specify the algorithms. Dr. AMIT KUMAR @JUET
- 3. Algorithms • The word algorithm comes from the name of a Persian mathematician Abu Ja’far Mohammed ibn-i Musa al Khowarizmi. • In computer science, this word refers to a special method useable by a computer for solution of a problem. The statement of the problem specifies in general terms the desired input/output relationship. • For example, sorting a given sequence of numbers into nondecreasing order provides fertile ground for introducing many standard design techniques and analysis tools. Dr. AMIT KUMAR @JUET
- 4. The problem of sorting Dr. AMIT KUMAR @JUET
- 5. Insertion Sort Dr. AMIT KUMAR @JUET
- 6. Example of Insertion Sort Dr. AMIT KUMAR @JUET
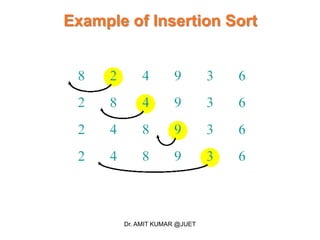
- 7. Example of Insertion Sort Dr. AMIT KUMAR @JUET
- 8. Example of Insertion Sort Dr. AMIT KUMAR @JUET
- 9. Example of Insertion Sort Dr. AMIT KUMAR @JUET
- 10. Example of Insertion Sort Dr. AMIT KUMAR @JUET
- 11. Example of Insertion Sort Dr. AMIT KUMAR @JUET
- 12. Example of Insertion Sort Dr. AMIT KUMAR @JUET
- 13. Example of Insertion Sort Dr. AMIT KUMAR @JUET
- 14. Example of Insertion Sort Dr. AMIT KUMAR @JUET
- 15. Example of Insertion Sort Dr. AMIT KUMAR @JUET
- 16. Example of Insertion Sort Dr. AMIT KUMAR @JUET
- 17. Analysis of algorithms The theoretical study of computer-program performance and resource usage. What’s more important than performance? • modularity • correctness • maintainability • functionality • robustness • user-friendliness • programmer time • simplicity • extensibility • reliabilityDr. AMIT KUMAR @JUET
- 18. Analysis of algorithms Why study algorithms and performance? • Algorithms help us to understand scalability. • Performance often draws the line between what is feasible and what is impossible. • Algorithmic mathematics provides a language for talking about program behavior. • The lessons of program performance generalize to other computing resources. • Speed is fun! Dr. AMIT KUMAR @JUET
- 19. Running Time • The running time depends on the input: an already sorted sequence is easier to sort. • Parameterize the running time by the size of the input, since short sequences are easier to sort than long ones. • Generally, we seek upper bounds on the running time, because everybody likes a guarantee. Dr. AMIT KUMAR @JUET
- 20. Kinds of analyses Worst-case: (usually) • T(n) = maximum time of algorithm on any input of size n. Average-case: (sometimes) • T(n) = expected time of algorithm over all inputs of size n. • Need assumption of statistical distribution of inputs. Best-case: • Cheat with a slow algorithm that works fast on some input. Dr. AMIT KUMAR @JUET
- 21. Machine-Independent time The RAM Model Machine independent algorithm design depends on a hypothetical computer called Random Acces Machine (RAM). Assumptions: • Each simple operation such as +, -, if ...etc takes exactly one time step. • Loops and subroutines are not considered simple operations. • Each memory acces takes exactly one time step. Dr. AMIT KUMAR @JUET
- 22. Machine-independent time What is insertion sort’s worst-case time? • It depends on the speed of our computer, • relative speed (on the same machine), • absolute speed (on different machines). BIG IDEA: • Ignore machine-dependent constants. • Look at growth of “Asymptotic Analysis” nnT as)( Dr. AMIT KUMAR @JUET
- 23. Machine-independent time: An example A pseudocode for insertion sort ( INSERTION SORT ). INSERTION-SORT(A) 1 for j 2 to length [A] 2 do key A[ j] 3 Insert A[j] into the sortted sequence A[1,..., j-1]. 4 i j – 1 5 while i > 0 and A[i] > key 6 do A[i+1] A[i] 7 i i – 1 8 A[i +1] key Dr. AMIT KUMAR @JUET
- 24. Analysis of INSERTION-SORT(contd.) 1]1[8 )1(17 )1(][]1[6 ][05 114 10]11[sequence sortedtheinto][Insert3 1][2 ][21 timescostSORT(A)-INSERTION 8 27 26 25 4 2 1 nckeyiA tcii tciAiA tckeyiAandi ncji njA jA ncjAkey ncAlengthj n j j n j j n j j do while do tofor Dr. AMIT KUMAR @JUET
- 25. Analysis of INSERTION-SORT(contd.) )1()1()1()( 2 6 2 5421 n j j n j j tctcncnccnT ).1()1( 8 2 7 nctc n j j The total running time is Dr. AMIT KUMAR @JUET
- 26. Analysis of INSERTION-SORT(contd.) The best case: The array is already sorted. (tj =1 for j=2,3, ...,n) )1()1()1()1()( 85421 ncncncncncnT ).()( 854285421 ccccnccccc Dr. AMIT KUMAR @JUET
- 27. Analysis of INSERTION-SORT(contd.) •The worst case: The array is reverse sorted (tj =j for j=2,3, ...,n). )12/)1(()1()( 521 nncncncnT )1()2/)1(()2/)1(( 876 ncnncnnc ncccccccnccc )2/2/2/()2/2/2/( 8765421 2 765 2 )1( 1 nn j n j cbnannT 2 )( Dr. AMIT KUMAR @JUET
- 28. Growth of Functions Although we can sometimes determine the exact running time of an algorithm, the extra precision is not usually worth the effort of computing it. For large inputs, the multiplicative constants and lower order terms of an exact running time are dominated by the effects of the input size itself. Dr. AMIT KUMAR @JUET
- 29. Asymptotic Notation The notation we use to describe the asymptotic running time of an algorithm are defined in terms of functions whose domains are the set of natural numbers ...,2,1,0N Dr. AMIT KUMAR @JUET
- 30. O-notation • For a given function , we denote by the set of functions • We use O-notation to give an asymptotic upper bound of a function, to within a constant factor. • means that there existes some constant c s.t. is always for large enough n. )(ng ))(( ngO 0 0 allfor)()(0 s.t.andconstantspositiveexistthere:)( ))(( nnncgnf ncnf ngO ))(()( ngOnf )(ncg)(nf Dr. AMIT KUMAR @JUET
- 31. Ω-Omega notation • For a given function , we denote by the set of functions • We use Ω-notation to give an asymptotic lower bound on a function, to within a constant factor. • means that there exists some constant c s.t. is always for large enough n. )(ng ))(( ng 0 0 allfor)()(0 s.t.andconstantspositiveexistthere:)( ))(( nnnfncg ncnf ng ))(()( ngnf )(nf )(ncg Dr. AMIT KUMAR @JUET
- 32. -Theta notation • For a given function , we denote by the set of functions • A function belongs to the set if there exist positive constants and such that it can be “sand- wiched” between and or sufficienly large n. • means that there exists some constant c1 and c2 s.t. for large enough n. )(ng ))(( ng 021 021 allfor)()()(c0 s.t.and,,constantspositiveexistthere:)( ))(( nnngcnfng nccnf ng )(nf ))(( ng 1c 2c )(1 ngc )(2 ngc Θ ))(()( ngnf )()()( 21 ngcnfngc Dr. AMIT KUMAR @JUET
- 33. Asymptotic notation Graphic examples of and . ,, O Dr. AMIT KUMAR @JUET
- 34. 2 2 22 1 3 2 1 ncnnnc 21 3 2 1 c n c Example 1. Show that We must find c1 and c2 such that Dividing bothsides by n2 yields For )(3 2 1 )( 22 nnnnf )(3 2 1 ,7 22 0 nnnn Dr. AMIT KUMAR @JUET
- 35. Theorem • For any two functions and , we have if and only if )(ng ))(()( ngnf )(nf )).(()(and))(()( ngnfngOnf Dr. AMIT KUMAR @JUET
- 36. Because : )2(5223 nnn Example 2. )2(5223)( nnnnf )2(5223 nOnn Dr. AMIT KUMAR @JUET
- 37. Example 3. 610033,3forsince)(61003 2222 nnncnOnn Dr. AMIT KUMAR @JUET
- 38. Example 3. 3when61003,1forsince)(61003 610033,3forsince)(61003 2332 2222 nnnncnOnn nnncnOnn Dr. AMIT KUMAR @JUET
- 46. Standard notations and common functions • Floors and ceilings 11 xxxxx Dr. AMIT KUMAR @JUET
- 47. Standard notations and common functions • Logarithms: )lg(lglglg )(loglog logln loglg 2 nn nn nn nn kk e Dr. AMIT KUMAR @JUET
- 48. Standard notations and common functions • Logarithms: For all real a>0, b>0, c>0, and n b a a ana baab ba c c b b n b ccc ab log log log loglog loglog)(log log Dr. AMIT KUMAR @JUET
- 49. Standard notations and common functions • Logarithms: b a ca aa a b ac bb bb log 1 log log)/1(log loglog Dr. AMIT KUMAR @JUET
- 50. Standard notations and common functions • Factorials For the Stirling approximation: ne n nn n 1 12! 0n )lg()!lg( )2(! )(! nnn n non n n Dr. AMIT KUMAR @JUET






















![Machine-independent time: An example
A pseudocode for insertion sort ( INSERTION SORT ).
INSERTION-SORT(A)
1 for j 2 to length [A]
2 do key A[ j]
3 Insert A[j] into the sortted sequence A[1,..., j-1].
4 i j – 1
5 while i > 0 and A[i] > key
6 do A[i+1] A[i]
7 i i – 1
8 A[i +1] key
Dr. AMIT KUMAR @JUET](https://image.slidesharecdn.com/algorithmanalysisinsertionsortandasymptoticnotations-180514052317/85/Algorithm-analysis-insertion-sort-and-asymptotic-notations-23-320.jpg)
![Analysis of INSERTION-SORT(contd.)
1]1[8
)1(17
)1(][]1[6
][05
114
10]11[sequence
sortedtheinto][Insert3
1][2
][21
timescostSORT(A)-INSERTION
8
27
26
25
4
2
1
nckeyiA
tcii
tciAiA
tckeyiAandi
ncji
njA
jA
ncjAkey
ncAlengthj
n
j j
n
j j
n
j j
do
while
do
tofor
Dr. AMIT KUMAR @JUET](https://image.slidesharecdn.com/algorithmanalysisinsertionsortandasymptoticnotations-180514052317/85/Algorithm-analysis-insertion-sort-and-asymptotic-notations-24-320.jpg)

























