Algorithms required for data structures(basics like Arrays, Stacks ,Linked Lists etc)

Definition
An algorithm is any well-defined
computational procedure that
takes some values or set of values
as input and produces some values
or set of values as output

Definition
A sequence of computational steps
that transforms the input into
output

4
Algorithms
Properties of algorithms:
• Input from a specified set,
• Output from a specified set (solution),
• Definiteness of every step in the computation,
• Correctness of output for every possible input,
• Finiteness of the number of calculation steps,
• Effectiveness of each calculation step and
• Generality for a class of problems.

?
Suppose computers were infinitely fast and
computer memory are free
Is there any reason to study algorithm ?
Yes
– Demonstrate that solution methods
terminates and does so with correct
answer.

In reality
• Computers may be fast, but
they are not infinitely fast and
• Memory may be cheap but it is
not free
• Computing time is therefore a
bounded resource and so is the
space in memory

7
Complexity
In general, we are not so much interested
in the time and space complexity for small
inputs.
For example, while the difference in time
complexity between linear and binary
search is meaningless for a sequence with
n=10, it is gigantic for n=230.

8
Complexity
For example, let us assume two algorithms A and
B that solve the same class of problems.
The time complexity of A is 5000n, the one for B
is 1.1n for an input with n elements.
For n = 10, A requires 50,000 steps, but B only
3, so B seems to be superior to A.
For n = 1000, however, A requires 50,00,000
steps, while B requires 2.5x1041 steps.

9
Complexity
Comparison: time complexity of algorithms A and B
Algorithm A Algorithm BInput Size
n
10
100
1,000
1,000,000
5,000n
50,000
5,00,000
50,00,000
5x109
1.1n
3
2.5x1041
13,781
4.8x1041392

10
Complexity
• This means that algorithm B cannot be used
for large inputs, while algorithm A is still
feasible.
• So what is important is the growth of the
complexity functions.
• The growth of time and space complexity with
increasing input size n is a suitable measure
for the comparison of algorithms.

Asymptotic Efficiency
Algorithm
• When the input size is large enough so that
the rate of growth/order of growth of the
running time is relevant.
• That is we are concerned with how the
running time of an algorithm increases as the
size of the input increases without bound.
• Usually, an algorithm that is asymptotically
more efficient will be the best choice. 11

Asymptotic Notation
The notations we use to describe
the asymptotic running time of an
algorithm are defined in terms of
functions whose domains are the
set of natural numbers N = {0, 1,
2,…. }
12

13
Asymptotic Notation
Let f(n) and g(n) be two positive
functions, representing the number
of basic calculations (operations,
instructions) that an algorithm
takes (or the number of memory
words an algorithm needs).

Asymptotic Notation
Q - Big Theta
O – Big O
W - Big Omega
o – Small o
w - Small Omega
14

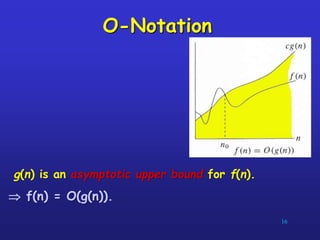
15
O-Notation
For a given function g(n)
O(g(n)) = {f(n) : there exist
positive constants c and n0 such
that 0  f(n)  c. g(n) for all n 
n0 }
Intuitively: Set of all functions whose rate of
growth is the same as or lower than that of
c. g(n)

O-Notation
16
g(n) is an asymptotic upper bound for f(n).
 f(n) = O(g(n)).

Example
O(g(n)) = {f(n) : there exist positive
constants c and n0 such that 0  f(n) 
c g(n) for all n  n0 }
f(n) = 5n+2
0  5n+2  6n
n=0  020 (no)
n=1  076 (no)
n=2  01212 (yes)
n=3  01718 (yes)
17
So n0=2, c=6, g(n)=n
 f(n)= O(n)

18
Big-O Notation
(Examples)
• f(n) = 5n+2 = O(n)
• f(n)=n/2 –3
0  n/2 –3  n/2; n0=6; c=1/2; f(n)=O(n)
• f(n) = n2-n
0  n2–n  n2; n0=0; c=1; f(n)=O(n2)
• f(n) = n(n+1)/2 = O(n2)

W - Notation
For a given function g(n)
W(g(n)) = {f(n) : there exist
positive constants c and n0 such
that 0  c g(n)  f(n) for all
n  n0}
19
Intuitively: Set of all functions whose
rate of growth is the same as or higher
than that of c.g(n).

W - Notation
20
g(n) is an asymptotic lower bound for f(n).
 f(n) = W(g(n)).

Example
W(g(n)) = {f(n) : there exist positive
constants c and n0 such that 0  c g(n) 
f(n) for all n  n0}
f(n) = 5n+2
0  5n  5n+2
n=0  002 (yes)
n=1  057 (yes)
n=2  01012 (yes)
21
So n0=0, c=5, g(n)=n
 f(n)= W(n)

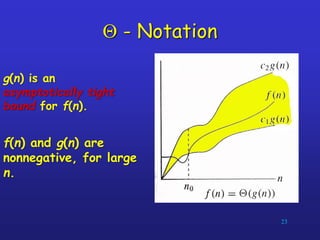
Q - Notation
For a given function g(n),
Q(g(n)) = {f(n) : there exist positive
constants c1 , c2 , and n0 such
that 0  c1 g(n)  f(n)  c2 g(n)
for all n  n0
f(n)  Q(g(n)) f(n) = Q(g(n))
22

Q - Notation
23
g(n) is an
asymptotically tight
bound for f(n).
f(n) and g(n) are
nonnegative, for large
n.

Example
Q(g(n)) = {f(n) :  positive constants c1, c2,
and n0, such that n  n0, 0  c1g(n) 
f(n)  c2g(n) }
• 5n+2 = Q(n)
Determine the positive constant n0,
c1, and c2 such that the above
conditions satisfies
5n  5n+2  6n
24

Example Contd ...
5n  5n+2 is true for all n  0
5n+2  6n is true for all n2
 5n  5n+2  6n is true for all
n2
 c1=5, c2=6, n0=2, g(n)=n
 f(n)= Q(g(n)) = Q(n)
25

Relations Between Q, O, W
For any two function f(n) and g(n),
we have f(n) = Q(g(n)) if and only if
f(n) = O(g(n)) and f(n) = W(g(n))
That is
Q(g(n)) = O(g(n))  W(g(n))
26

28
The Growth of Functions
“Popular” functions g(n) are
n.log n, 1, 2n, n2, n!, n, n3, log n
Listed from slowest to fastest growth:
• 1
• log n
• n
• n log n
• n2
• n3
• 2n
• n!

Comparing Growth Rates
Problem Size
T(n)
log2 n
n
n log2 n
n22n

Example: Find sum of array elements
Input size: n (number of array elements)
Total number of steps: 2n + 3 = f(n)
Algorithm arraySum (A, n)
Input array A of n integers
Output Sum of elements of A # operations
sum  0 1
for i  0 to n  1 do n+1
sum  sum + A [i] n
return sum 1

Algorithm arrayMax(A, n)
Input array A of n integers
Output maximum element of A # operations
currentMax  A[0] 1
for i  1 to n  1 do n
if A [i]  currentMax then n -1
currentMax  A [i] n -1
return currentMax 1
Example: Find max element of an
array
 Input size: n (number of array elements)
 Total number of steps: f(n)=3n

Algorithms required for data structures(basics like Arrays, Stacks ,Linked Lists etc)

More Related Content

What's hot (20)

Similar to Algorithms required for data structures(basics like Arrays, Stacks ,Linked Lists etc) (20)

Recently uploaded (20)

Algorithms required for data structures(basics like Arrays, Stacks ,Linked Lists etc)