An Introduction to Network Theory

An Introduction to Network Theory Kyle Findlay [email_address] R&D Executive TNS Global Brand Equity Centre Presented at the SAMRA 2010 Conference Mount Grace Country House and Spa, Magaliesburg, South Africa, from 2 to 5 June 2010

What is a network? An agent/object's actions are affected by the actions of others around it. Actions, choices, etc. are not made in isolation i.e. they are contingent on others' actions, choices, etc.

“ A collection of objects connected to each other in some fashion” [Watts, 2002]

Social groups The internet Cities What is a network? Diseases Neural networks (computer & human) Proteins & genes Stem cells Other cells Plants Source: Six Degrees, Duncan Watts, 2002 The blogosphere Proliferation of landlines in London Human genome Quaking Aspen (one of the largest organisms in the world – these trees represent a single organism with a shared root system) Rabbit cell

New paradigm : “real networks represent populations of individual components that are actually doing something ” [Watts, 2002] In other words, networks are dynamic objects that are continually changing Understanding a network is important because its structure affects the individual components’ behaviour and the behaviour of the system as a whole Networks are key to understanding non-linear , dynamic systems … … just like those represented by almost every facet of the universe … … from the atomic level right through to the cosmic level The important part is that the components are not acting independently – they are affected by the components around them ! Note: links between component may be physical (e.g. power cable, magnetism) or conceptual (e.g. social connections) Networks used to be thought of as fixed structures What is a network?

Shipping (sea) networks Telecommunications networks Air traffic network Data networks Source: Britain From Above ( http:// www.bbc.co.uk/britainfromabove ) CAUTION: Gratuitous network shots

Network thinking can be applied almost anywhere !

Epidemiology (i.e. spread of diseases) e.g. spread of foot & mouth disease in the UK in 2001 over 75 days Where’s it applied? URL: http:// www.youtube.com/watch?v =PufTeIBNRJ4

Physics e.g. particle interactions, the structure of the universe Where’s it applied? URL: http:// www.youtube.com/watch?v =8C_dnP2fvxk

Engineering e.g. creation of robust infrastructure (e.g. electricity, telecoms), rust formation (natural growth processes similar to diffusion limited aggregation) Where’s it applied? URL: http:// www.youtube.com/watch?v =lRZ2iEHFgGo URL: http:// www.youtube.com/watch?v = AEoP-XtJueo

Technology e.g. mapping the online world, making networks resilient in the face of cyber-terrorism, optimising cellular networks, controlling air traffic Where’s it applied? URL: http:// www.youtube.com/watch?v =l-RoDv7c5ok URL: http:// www.youtube.com/watch?v =o4g930pm8Ms Vid not working

Biology e.g. fish swimming in schools, ant colonies, birds flying in formation, crickets chirping in unison, giant honeybees shimmering Where’s it applied? URL: http:// www.youtube.com/watch?v =Sp8tLPDMUyg URL: http:// www.youtube.com/watch?v =YadP3w7vkJA

Medicine e.g. cell formation, nervous system, neural networks Where’s it applied? Source: The Human Brain Book by Rita Carter

And, most interestingly…society e.g. interactions between people (e.g. Facebook; group behaviour) Where’s it applied? URL: http:// www.youtube.com/watch?v =9n9irapdON4 URL: http:// www.youtube.com/watch?v =sD2yosZ9qDw

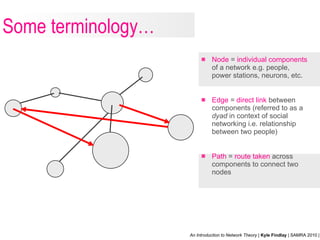
Node = individual components of a network e.g. people, power stations, neurons, etc. Edge = direct link between components (referred to as a dyad in context of social networking i.e. relationship between two people) Path = route taken across components to connect two nodes Some terminology…

Tells you how likely a node is to be connected to its neighbours … … and, importantly, how likely that its neighbours are connected to each other Put another way, it tells you how close a node and its neighbors are to being a clique where “everybody knows everyone else” Important network features: Clustering co-efficient No connections between nodes c = 0 Some nodes connected c = 1/3 All relevant nodes connected c = 1

“ Unclustered” network “ Clustered” network *Source: Six Degrees, Duncan Watts, 2002 None of Ego’s friends know each other* All of Ego’s friends know each other Important network features: Clustering co-efficient

A real-world example: CEOs of Fortune 500 companies Which companies share directors? Clusters are colour-coded Source: http://flickr.com/photos/11242012@N07/1363558436 Important network features: Clustering co-efficient

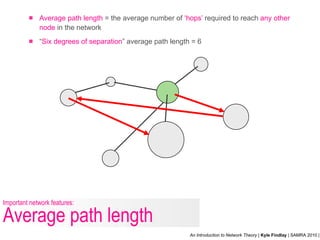
Average path length = the average number of ‘hops’ required to reach any other node in the network “ Six degrees of separation ” average path length = 6 Important network features: Average path length

The degree of a node is the number of connections (or edges) it has coming in from, and going out to, other nodes Node 10 connections or “ edges ” Important network features: Degree distribution 3 2 1 4 5 6 7 8 10 9

They sit on a continuum based on a few factors: *Source: Six Degrees, Duncan Watts, 2002 3 main types of networks 2 Clustering 3 Ave path length 1 Randomness Grid/lattice network (structure, order) Small-world network (a mix of order and randomness) Random network (randomness) << Level of randomness of links >> β=0 β=1

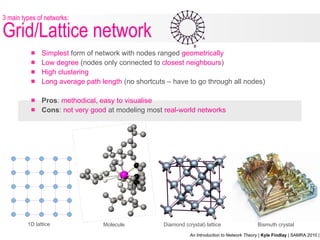
Simplest form of network with nodes ranged geometrically Low degree (nodes only connected to closest neighbours ) High clustering Long average path length (no shortcuts – have to go through all nodes) Pros : methodical , easy to visualise Cons : not very good at modeling most real-world networks 3 main types of networks: Grid/Lattice network Molecule 1D lattice Diamond (crystal) lattice Bismuth crystal

Most nodes aren’t neighbours , but they can be reached from every other node by a small number of hops or steps i.e. small average path length due to a few random re-wirings 3 main types of networks: Small world network Source: http://en.wikipedia.org/wiki/Small-world_network Higher clustering co-efficient than one would expect if connections were made by pure random chance “ A small world network, where nodes represent people and edges connect people that know each other, captures the small world phenomenon of strangers being linked by a mutual acquaintance ” Common in nature , including everything from the internet to gene regulatory networks to ecosystems

Lower clustering than small-world networks generally No “force” or “bias” influencing how links are created between nodes i.e. probability of creating an edge/link is independent of previous connections 3 main types of networks: Random network

Nature Networks are evident everywhere in nature In fact, most natural growth processes come about due to network behaviour The big picture Natural growth = evolutionary , iterative growth , where future growth is constrained by previous growth patterns (referred to as path dependence ) i.e. growth follows the network structure

Networks better reflect reality and capture complexity i.e. non-linear dynamics Network theory helps us to better understand: And market research? How will word of my brand permeate through my target market? ? How will negative publicity about my brand spread and be interpreted? ? Who are the gatekeepers in a community that most affect the flow of information ? ? How is the market likely to fall out in terms of market share (Double Jeopardy)? ? What will the non-linear impact be of a specific change in the market e.g. change in market share, perceptions, etc. ?

Network theory has been used to understand imagery and market barriers Adjusting attributes and seeing knock-on effect in network Using agent-based modeling to model this effect And market research? Useful for word-of-mouth / viral approaches Watts and Peretti use network theory to increase reach of WOM campaigns Helps us avoid thinking about things in a vacuum as it takes account of inter-related variables… … and provides us with counter-intuitive outcomes that we may not have reached on our own

Next: Interesting discussion points… End of main presentation

This is a very simple 2D representation of how I roughly visualise information propagating through a network It is very simple and doesn’t take into account many concepts But it is a visual aid that helps one to start thinking about how information might spread from person to person Some interesting bits: A network in action Source: http://www.funny-games.biz/reaction-effect.html

What does a highly “spreadable” idea look like? 1,636,967 views in two months (as at 25 April 2010) Performed in front of 75,000 people at Coachella Music Festival (California, April 2010) URL: http:// www.youtube.com/watch?v =Q77YBmtd2Rw Some interesting bits: How ideas spread

Some interesting bits: How ideas spread Who spreads ideas? Watts vs. Gladwell Mavens/influencers vs. forest fire Self-organised criticality K-shell decomposition? vs.

Which ideas spread? Unpredictable Ideas that “fit” Some interesting bits: How ideas spread

Refers to systems in which many individual agents with limited intelligence and information are able to pool resources to accomplish a goal beyond the capabilities of the individuals… while only focused on self-interest without the bigger picture in mind Some interesting bits: Distributed intelligence e.g. no single ant knows how to build an ant colony e.g. the internet has grown organically over time with no single person directing its growth i.e. no grand designer This is known as self-organisation and/or emergence , and is a property of complex networks and non-linear, dynamic systems

Existence of such behaviour in organisms has many implications for social , military and management applications and is one of the most active areas of research today! Works best in small-world networks Implications for knowledge diffusion , memes , collaboration , etc. Some interesting bits: Distributed intelligence

Some interesting bits: Distributed intelligence Ant colony Source: http:// www.youtube.com/watch?v =ozkBd2p2piU URL: http:// www.youtube.com/watch?v =ozkBd2p2piU

“ On average, the first 5 random re-wirings reduce the average path length of the network by one-half , regardless of the size of the network ” [Watts, 2002]* *Source: Six Degrees, Duncan Watts, 2002, p.89 Random re-wirings Long average path length Dramatically reduced average path length Some interesting bits: Random re-wirings “ 8” “ 3”

People are more likely to become acquainted over time when they have something in common i.e. we have a bias towards the familiar , thus reducing the pure randomness of connections Known as “ homophily ” - “birds of a feather flock together” Network connections don’t arise independently of each other… … they are influenced by previous connections If A knows B… … and B knows C… … then A is much more likely to know C *Source: Six Degrees, Duncan Watts, 2002, p.58-61 A B C Some interesting bits: Triadic closure

*Source: Six Degrees, Duncan Watts, 2002, p.58-61 A B C This is why random re-wirings are so effective at reducing the ave. path length … … they help connect clusters, or ‘cliques’, that might otherwise exist in isolation This is the strength of the small-world network: High clustering and a relatively small amount of random re-wirings allows for a dramatically reduced average path length… … allowing everyone to connect to everyone else in relatively few steps e.g. “six degrees of separation” Some interesting bits: Triadic closure

*Source: Six Degrees, Duncan Watts, 2002, p.78-79 This “ birds of a feather flock together ” effect was modeled by Watts and Strogatz* They used α (alpha) to represent level of preference to only connect with friends of friends Low α = strong preference to only connect with friends of friends (triadic closures occur, independent clusters) High α = connections chosen at random Small-world networks exist somewhere around the peak (which represents a phase transition ) i.e. where clustering is high but average path length is low To the left of the peak, clusters are just starting to join together At the peak , everyone is connected To the right of the peak, connections are lost as wirings become more random Some interesting bits: Triadic closure

Studies conducted by Stanley Milgram beginning in 1967 at Harvard University Sent packages to randomly selected people in Omaha , Nebraska & Wichita Asked that they be delivered to individuals in Boston , Massachusetts Could only forward package to people they knew on a first-name basis Only 64 of 296 letters reached their destination Average path length of these was around 5.5 or 6 Milgram never used the phrase “six degrees of separation” himself Source: Wikipedia, Small world experiment Wikipedia, Six degrees of separation Milgram repeated other similar experiments which also received low completion rates However, experiments on the internet have since confirmed the number at 6: Facebook application: Six Degrees – 4.5 million users ; average path = 5.73 Some interesting bits: Six degrees of separation

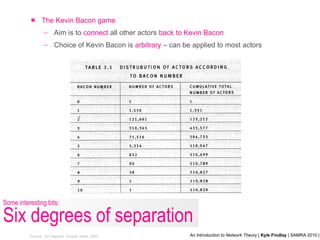
The Kevin Bacon game Aim is to connect all other actors back to Kevin Bacon Choice of Kevin Bacon is arbitrary – can be applied to most actors *Source: Six Degrees, Duncan Watts, 2002 Some interesting bits: Six degrees of separation

Some interesting bits: Six degrees of separation What’s your Erdős number? (Scientific equivalent of The Kevin Bacon Game) “ Apocalypse” by XKCD Alt text for this comic: "I wonder if I still have time to go shoot a short film with Kevin Bacon?" URL: http://xkcd.com/599/

A network is considered “ scale-free ” if its degree distribution follows a power law i.e. nodes can have an unlimited number of links to them e.g. the internet A few nodes have many links , while the majority have few links This is what a power law distribution looks like* If you take the log of both axes, you should get a straight line* *Image source: Six Degrees, Duncan Watts, 2002 Some interesting bits: Scale-free networks & power laws

However, very few , if any, networks can display scale-free properties indefinitely At some point, limited resources force a cut-off e.g. limited number of computers in the world Therefore, generally, scale-free networks only display a power law distribution for some area of the graph Taking the log-log of a power law distribution should show a straight line* However, in practice, the line is generally only straight for some area of the graph* *Image source: Six Degrees, Duncan Watts, 2002 Some interesting bits: Scale-free networks & power laws

Power law distributions help us understand natural growth (e.g. popularity of brands, trends, ideas, politics, religion, etc.) Growth in an environment where social influence occurs tends to result in a power law distribution (think cumulative advantage ) This comes about due to network behaviour e.g. nodes with more connections are more likely to have even more connections (sounds a lot like… Double Jeopardy !) This ‘ skewing ’ of growth patterns is characteristic of small world networks and results in a few large components and many small components In order to understand non-linear growth/dynamics, we need to understand the influence of the network on the individual components Power laws help us describe this influence And networks help us understand how power laws come about Some interesting bits: Scale-free networks & power laws

Software examples… http://www.youtube.com/watch?v=tYQovmtO06k&feature=related

Thanks! http://www.youtube.com/watch?v=tYQovmtO06k&feature=related It’s a small world after all 

An Introduction to Network Theory

More Related Content

What's hot (20)

Viewers also liked (6)

Similar to An Introduction to Network Theory (20)

More from Socialphysicist (14)

Recently uploaded (20)

An Introduction to Network Theory

Editor's Notes