An overview of gradient descent optimization algorithms

An overview of gradient descent
optimization algorithms
Ruder, Sebastian. "An overview of gradient descent optimization algorithms." arXiv preprint
arXiv:1609.04747 (2016).
Twitter : @St_Hakky

Overview of this paper
• Gradient descent optimization algorithms are often
used as black-box optimizers.
• This paper provides the reader with intuitions with
regard to the behavior of different algorithms that
will allow her to put them to use.

Contents
1. Introduction
2. Gradient descent variants
3. Challenges
4. Gradient descent optimization algorithms
5. Parallelizing and distributing SGD
6. Additional strategies for optimizing SGD
7. Conclusion

Gradient Descent is often used as
black-box tools
• Gradient descent is popular algorithm to perform
optimization of deep learning.
• Many Deep Learning library contains various gradient
descent algorithms.
• Example : Keras, Chainer, Tensorflow…
• However, these algorithms often used as black-box
tools and many people don’t understand their
strength and weakness.
• We will learn this.

Gradient Descent
• Gradient descent is a way to minimize an objective
function 𝐽(𝜃)
• 𝐽(𝜃)： Objective function
• 𝜃 ∈ 𝑅 𝑑：Model’s parameters
• 𝜂：Learning rate. This determines the size of the steps
we take to reach a (local) minimum.
𝐽(𝜃)
𝜃
𝜃 = 𝜃 − 𝜂 ∗ 𝛻𝜃 𝐽(𝜃)
Update equation
𝛻𝜃 𝐽(𝜃)
𝑙𝑜𝑐𝑎𝑙 𝑚𝑖𝑛𝑖𝑚𝑢𝑚
𝜃∗

Gradient descent variants
• There are three variants of gradient descent.
• Batch gradient descent
• Stochastic gradient descent
• Mini-batch gradient descent
• The difference of these algorithms is the amount of
data.
𝜃 = 𝜃 − 𝜂 ∗ 𝛻𝜃 𝐽(𝜃)
Update equation
This term is different
with each method

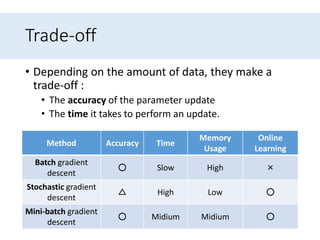
Trade-off
• Depending on the amount of data, they make a
trade-off :
• The accuracy of the parameter update
• The time it takes to perform an update.
Method Accuracy Time
Memory
Usage
Online
Learning
Batch gradient
descent
○ Slow High ×
Stochastic gradient
descent
△ High Low ○
Mini-batch gradient
descent
○ Midium Midium ○

Batch gradient descent
This method computes the gradient of the cost function
with the entire training dataset.
𝜃 = 𝜃 − 𝜂 ∗ 𝛻𝜃 𝐽(𝜃)
Update equation
Code
We need to calculate the
gradients for the whole dataset
to perform just one update.

Batch gradient descent
• Advantage
• It is guaranteed to converge to the global minimum for
convex error surfaces and to a local minimum for non-
convex surfaces.
• Disadvantages
• It can be very slow.
• It is intractable for datasets that do not fit in memory.
• It does not allow us to update our model online.

Stochastic gradient descent
This method performs a parameter update for each training
example 𝑥 𝑖 and label 𝑦(𝑖).
𝜃 = 𝜃 − 𝜂 ∗ 𝛻𝜃 𝐽(𝜃; 𝑥 𝑖 ; 𝑦(𝑖))
Update equation
Code
We need to calculate the
gradients for the whole dataset
to perform just one update.
Note : we shuffle the training data at every epoch

Stochastic gradient descent
• Advantage
• It is usually much faster than batch gradient descent.
• It can be used to learn online.
• Disadvantages
• It performs frequent updates with a high variance that
cause the objective function to fluctuate heavily.

The fluctuation : Batch vs SGD
・Batch gradient descent converges to
the minimum of the basin the
parameters are placed in and the
fluctuation is small.
https://wikidocs.net/3413
・SGD’s fluctuation is large but it
enables to jump to new and
potentially better local minima.
However, this ultimately complicates
convergence to the exact minimum,
as SGD will keep overshooting

Learning rate of SGD
• When we slowly decrease the learning rate, SGD
shows the same convergence behaviour as batch
gradient descent
• It almost certainly converging to a local or the global
minimum for non-convex and convex optimization
respectively.

Mini-batch gradient descent
This method takes the best of both batch and SGD, and
performs an update for every mini-batch of 𝑛.
𝜃 = 𝜃 − 𝜂 ∗ 𝛻𝜃 𝐽(𝜃; 𝑥 𝑖:𝑖+𝑛 ; 𝑦(𝑖:𝑖+𝑛))
Update equation
Code

Mini-batch gradient descent
• Advantage :
• It reduces the variance of the parameter updates.
• This can lead to more stable convergence.
• It can make use of highly optimized matrix optimizations
common to deep learning libraries that make computing
the gradient very efficiently.
• Disadvantage :
• We have to set mini-batch size.
• Common mini-batch sizes range between 50 and 256, but can
vary for different applications.

Challenges
• Mini-batch gradient descent offers a few challenges.
• Choosing a proper learning rate is difficult.
• The settings of learning rate schedule is difficult.
• Changing learning rate for each parameter is difficult.
• Avoiding getting trapped in highly non-convex error
functions’ numerous suboptimal local minima is difficult

Choosing a proper learning rate can be difficult
• Learning rate is too small
• => This is painfully slow convergence
• Learning rate is too large
• => This can hinder convergence and cause the loss
function to fluctuate around the minimum or even to
diverge.
• Problem : How do we set learning rate?

The settings of learning rate schedule is difficult
• When we use learning rate schedules method, we
have to define schedules and thresholds in
advance
• They are unable to adapt to a dataset’s characteristics.

Changing learning rate for each
parameter is difficult
• Situation :
• Data is sparse
• Features have very different frequencies
• What we want to do :
• we might not want to update all of them to the same
extent.
• Problem :
• If we update parameters at the same learning late, it
performs a larger update for rarely occurring features.

Avoiding getting trapped in highly non-convex error
functions’ numerous suboptimal local minima
• Dauphin[5] argue that the difficulty arises in fact not
from local minima but from saddle points.
• Saddle points are at the places that one dimension slopes
up and another slopes down.
• These saddle points are usually surrounded by a
plateau of the same error as the gradient is close to
zero in all dimensions.
• This makes it hard for SGD to escape.
[5] Yann N. Dauphin, Razvan Pascanu, Caglar Gulcehre, Kyunghyun Cho, Surya Ganguli, and Yoshua Bengio. Identifying and
attacking the saddle point problem in high-dimensional nonconvex optimization. arXiv, pages 1–14, 2014.

Gradient descent optimization algorithms
• To deal with the challenges, some algorithms are
widely used by the Deep Learning community.
• Momentum
• Nesterov accelerated gradient
• Adagrad
• Adadelta
• RMSprop
• Adam
• Visualization of algorithms
• Which optimizer to use?

The difficulty of SGD
• SGD has trouble navigating ravines which are
common around local optima.
Areas where the surface curves much more steeply in one
dimension than in another is very difficult for SGD.

The difficulty of SGD
• SGD oscillates across the slopes of the ravine while
only making hesitant progress along the bottom
towards the local optimum.

Momentum
Momentum is a method that helps accelerate SGD.
It does this by adding a fraction 𝛾 of the update vector
of the past time step to the current update vector.
The momentum term 𝛾 is usually
set to 0.9 or a similar value.

Momentum
Momentum is a method that helps accelerate SGD.
It does this by adding a fraction 𝛾 of the update vector of the
past time step to the current update vector
The momentum term 𝛾 is usually
set to 0.9 or a similar value.
The ball accumulates momentum as it
rolls downhill, becoming faster and
faster on the way.

Visualize Momentum
• https://www.youtube.com/watch?v=7HZk7kGk5bU

Why Momentum Really Works
Demo : http://distill.pub/2017/momentum/
The momentum term increases for dimensions whose
gradients point in the same directions.
The momentum term reduces updates for
dimensions whose gradients change directions.

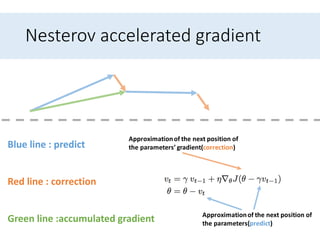
Nesterov accelerated gradient
• However, a ball that rolls down a hill, blindly
following the slope, is highly unsatisfactory.
• We would like to have a smarter ball that has a
notion of where it is going so that it knows to slow
down before the hill slopes up again.
• Nesterov accelerated gradient gives us a way of it.

Approximation of the next position of
the parameters(predict)

the parameters’ gradient(correction)

Blue line : predict
Red line : correction
Green line :accumulated gradient Approximationof the next position of
Approximationof the next position of
the parameters’ gradient(correction)

• This anticipatory update prevents us from going
too fast and results in increased responsiveness.
• Now , we can adapt our updates to the slope of our
error function and speed up SGD in turn.

What’s next…?
• We also want to adapt our updates to each
individual parameter to perform larger or smaller
updates depending on their importance.
• Adagrad
• Adadelta
• RMSprop
• Adam

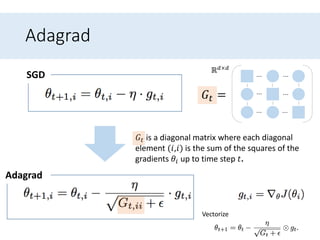
Adagrad
• Adagrad adapts the learning rate to the parameters
• Performing larger updates for infrequent
• Performing smaller updates for frequent parameters.
• Ex.
• Training large-scale neural nets at Google that learned to
recognize cats in Youtube videos.

Different learning rate for every parameter
• Previous methods :
• we used the same learning rate 𝜼 for all parameters 𝜽
• Adagrad :
• It uses a different learning rate for every parameter 𝜃𝑖 at
every time step 𝑡

Adagrad
Adagrad
SGD
𝐺𝑡 =
ℝ 𝑑×𝑑
⋯ ⋯
⋯ ⋯
⋯ ⋯
⋯⋯
⋯
⋯⋯
⋯
Vectorize

Adagrad
Adagrad
SGD
Adagrad modifies the general learning
rate 𝜼 based on the past gradients
that have been computed for 𝜽𝒊
𝐺𝑡 =
ℝ 𝑑×𝑑
⋯ ⋯
⋯ ⋯
⋯ ⋯
⋯⋯
⋯
⋯⋯
⋯
Vectorize

Adagrad
Adagrad
SGD
𝐺𝑡 is a diagonal matrix where each diagonal
element (𝑖,𝑖) is the sum of the squares of the
gradients 𝜃𝑖 up to time step 𝑡.
𝐺𝑡 =
ℝ 𝑑×𝑑
⋯ ⋯
⋯ ⋯
⋯ ⋯
⋯⋯
⋯
⋯⋯
⋯
Vectorize

Adagrad
Adagrad
SGD
𝜀 is a smoothing term that avoids division by
zero (usually on the order of 1e − 8).
𝐺𝑡 =
ℝ 𝑑×𝑑
⋯ ⋯
⋯ ⋯
⋯ ⋯
⋯⋯
⋯
⋯⋯
⋯
Vectorize

Adagrad’s advantages
• Advantages :
• It is well-suited for dealing with sparse data.
• It greatly improved the robustness of SGD.
• It eliminates the need to manually tune the learning rate.

Adagrad’s disadvantage
• Disadvantage :
• Main weakness is its accumulation of the squared
gradients in the denominator.

Adagrad’s disadvantage
• The disadvantage causes the learning rate to shrink
and become infinitesimally small. The algorithm
can no longer acquire additional knowledge.
• The following algorithms aim to resolve this flaw.
• Adadelta
• RMSprop
• Adam

Adadelta : extension of Adagrad
• Adadelta is an extension of Adagrad.
• Adagrad :
• It accumulate all past squared gradients.
• Adadelta :
• It restricts the window of accumulated past gradients to
some fixed size 𝑤.

Adadelta
• Instead of inefficiently storing, the sum of gradients
is recursively defined as a decaying average of all
past squared gradients.
• 𝐸[𝑔2] 𝑡 ：The running average at time step 𝑡.
• 𝛾 : A fraction similarly to the Momentum term, around
0.9

Adadelta
SGDAdagrad
Adadelta
Replace the diagonal matrix 𝐺𝑡 with the decaying
average over past squared gradients 𝐸[𝑔2] 𝑡

Adadelta
SGDAdagrad
Adadelta Adadelta
Replace the diagonal matrix 𝐺𝑡 with the decaying
average over past squared gradients 𝐸[𝑔2] 𝑡

Update units should have the same
hypothetical units
• The units in this update do not match and the
update should have the same hypothetical units as
the parameter.
• As well as in SGD, Momentum, or Adagrad
• To realize this, first defining another exponentially
decaying average

Adadelta
AdadeltaAdadelta
We approximate RMS with the RMS of
parameter updates until the previous time step.

Adadelta update rule
• Replacing the learning rate 𝜂 in the previous update
rule with 𝑅𝑀𝑆[∆𝜃] 𝑡−1 finally yields the Adadelta
update rule:
• Note : we do not even need to set a default
learning rate

RMSprop
RMSprop and Adadelta have both been developed
independently around the same time to resolve
Adagrad’s radically diminishing learning rates.
RMSprop

RMSprop
RMSprop as well divides the learning rate by an
exponentially decaying average of squared gradients.
RMSprop
Hinton suggests 𝛾 to be set to 0.9, while a good
default value for the learning rate 𝜂 is 0.001.

Adam
• Adam’s feature :
• Storing an exponentially decaying average of past
squared gradients 𝑣 𝑡 like Adadelta and RMSprop
• Keeping an exponentially decaying average of past
gradients 𝑚 𝑡, similar to momentum.
The first moment (the mean)
The second moment (the
uncentered variance)

Adam
• As 𝑚 𝑡 and 𝑣 𝑡 are initialized as vectors of 0’s, they
are biased towards zero.
• Especially during the initial time steps
• Especially when the decay rates are small
• (i.e. β1 and β2 are close to 1).
• Counteracting these biases in Adam
Adam
Note : default values of 0.9 for 𝛽1,
0.999 for 𝛽2, and 10−8 for 𝜀

Visualization of algorithms
• As we can see, Adagrad, Adadelta, RMSprop, and
Adam are most suitable and provide the best
convergence for these scenarios.

Which optimizer to use?
• If your input data is sparse…?
• You likely achieve the best results using one of the
adaptive learning-rate methods.
• An additional benefit is that you will not need to tune
the learning rate

Which one is best? :
Adagrad/Adadelta/RMSpro/Adam
• Adagrad, RMSprop, Adadelta, and Adam are very
similar algorithms that do well in similar
circumstances.
• Kingma et al. show that its bias-correction helps
Adam slightly outperform RMSprop.
• Insofar, Adam might be the best overall choice.

Interesting Note
• Interestingly, many recent papers use SGD
• without momentum and a simple learning rate
annealing schedule.
• SGD usually achieves to find a minimum but it takes
much longer time than others.
• However, it is a robust initialization and schedule,
and may get stuck in saddle points rather than local
minima.

Parallelizing and distributing SGD
• Distributing SGD is an obvious choice to speed it up
further.
• Now, we can have much data and the availability of low-
commodity clusters.
• SGD is inherently sequential.
• If we run it step-by-step
• Good convergence
• Slow
• If we run it asynchronously
• Faster
• Suboptimal communication between workers can lead to poor
convergence.

Parallelizing and distributing SGD
• The following algorithms and architectures are for
optimizing parallelized and distributed SGD.
• Hogwild!
• Downpour SGD
• Delay-tolerant Algorithms for SGD
• TensorFlow
• Elastic Averaging SGD

Hogwild!
• This allows performing SGD updates in parallel on
CPUs.
• Processors are allowed to access shared memory
without locking the parameters
• Note : This only works if the input data is sparse

Downpour SGD
… …
Parameter server
Storing and Updating a fraction of the model’s parameters
Downpour SGD runs multiple replicas of a
model in parallel on subsets of the training data.
Send their updates
model

Downpour SGD
• However, as replicas don’t communicate with each
other e.g. by sharing weights or updates, their
parameters are continuously at risk of diverging,
hindering convergence.

Delay-tolerant Algorithms for SGD
• McMahan and Streeter [11] extend AdaGrad to the
parallel setting by developing delay-tolerant
algorithms that not only adapt to past gradients,
but also to the update delays.

TensorFlow
• Tensorflow is already used internally to perform
computations on a large range of mobile devices as
well as on large-scale distributed systems.
• It relies on a computation graph that is split into a
subgraph for every device, while communication
takes place using Send/Receive node pairs.

Elastic Averaging SGD(EASGD)
• Should read paper to understand this.
• Ioffe, Sergey, and Christian Szegedy. "Batch
normalization: Accelerating deep network training by
reducing internal covariate shift." arXiv preprint
arXiv:1502.03167 (2015).

Additional strategies for optimizing SGD
• Shuffling and Curriculum Learning
• Batch normalization
• Early stopping
• Gradient noise

Shuffling and Curriculum Learning
• Shuffling(Random shuffle)
• => To avoid providing the training examples in a
meaningful order because this may bias the optimization
algorithm.
• Curriculum learning(Meaningful order shuffle)
• => To solve progressively harder problems.

Batch normalization
• By making normalization part of the model
architecture, we can use higher learning rates and
pay less attention to the initialization parameters.
• Batch normalization additionally acts as a
regularizer, reducing the need for Dropout.

Early stopping
• According to Geoff Hinton
• “Early stopping (is) beautiful free lunch”
• In the training of each epoch, we use validation
data to check the learning is already convergence.
• If it is true, we stop the learning.

Gradient noise
Adding this noise makes networks more robust to poor
initialization and gives the model more chances to escape and
find new local minima.
Add noise to each gradient update
Annealing the variance according to the following schedule

Conclusion
• Gradient descent variants
• Batch/Mini-Batch/SGD
• Challenges for Gradient descent
• Gradient descent optimization algorithms
• Momentum/Nesterov accelerated gradient
• Adagrad/Adadelta/RMSprop/Adam
• Parallelizing and distributing SGD
• Hogwild!/Downpour SGD/Delay-tolerant Algorithms for
SGD/TensorFlow/Elastic Averaging SGD
• Additional strategies for optimizing SGD
• Shuffling and Curriculum Learning/Batch
normalization/Early stopping/Gradient noise

An overview of gradient descent optimization algorithms

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to An overview of gradient descent optimization algorithms (20)

More from Hakky St (18)

Recently uploaded (20)

An overview of gradient descent optimization algorithms

Editor's Notes