![Skewness
• Skewness is used to measure symmetry of data
along with the mean value. Symmetry means equal
distribution of observation above or below the mean.
• skewness = 0: if data is symmetric along with mean
• skewness = Negative: if data is not symmetric and
right side tail is longer than left side tail of density
plot.
• skewness = Positive: if data is not symmetric and
left side tail is longer than right side tail in density
plot.
• We can find skewness of given variable by below
given formula.
• data[‘A’].skew()](https://image.slidesharecdn.com/basicstatisticaldescriptionsofdata-241111121434-0b714641/85/Basic-Statistical-descriptions-of-Data-pptx-29-320.jpg)
Basic Statistical descriptions of Data.pptx
- 1. CS3352 & Foundations of Data Science Basic Statistical Descriptions of Data. Dr.M.Swarna Sudha Associate Professor/CSE Ramco Institute of Technology Rajapalayam
- 2. Statistics • Statistics studies the collection, analysis, interpretation or explanation, and presentation of data. • Data mining has an inherent connection with statistics. • A statistical model is a set of mathematical functions that describe the behavior of the objects in a target class in terms of random variables and their associated probability distributions.
- 3. • Statistics is useful for mining various patterns from data as well as for understanding the underlying mechanisms generating and affecting the patterns. • Inferential statistics (or predictive statistics) models data in a way that accounts for randomness and uncertainty in the observations and is used to draw inferences about the process or population under investigation
- 4. Dataset • A dataset in machine learning is, quite simply, a collection of data pieces that can be treated by a computer as a single unit for analytic and prediction purposes
- 8. Data Objects and Attribute Types • Data sets are made up of data objects. A data object represents an entity Example • Sales database, the objects may be customers, store items, and sales. • Medical database, the objects may be patients • University database, the objects may be students, professors, and courses. • Data objects can also be referred to as samples, examples, instances, data points, or objects.
- 9. What Is an Attribute? • An attribute is a data field, representing a characteristic or feature of a data object. • Attribute, dimension, feature, and variable are often used • The term dimension is commonly used in data warehousing. • Machine learning use the term feature, while statisticians prefer the term variable.
- 12. Attribute Types
- 16. Measuring the Central Tendency: Mean, Median, and Mode • Suppose that we have some attribute X, like salary, which has been recorded for a set of objects. Let x1,x2,...,xN be the set of N observed values or observations for X. • Here, these values may also be referred to as the data set (for X). • If we were to plot the observations for salary, where would most of the values fall? This gives us an idea of the central tendency of the data. • Measures of central tendency include the mean, median, mode, and midrange.
- 17. • The most common and effective numeric measure of the “center” of a set of data is the (arithmetic) mean. • Let x1,x2,...,xN be a set of N values or observations, such as for some numeric attribute X, like salary. • The mean of this set of values is
- 18. Examples • Mean. Suppose we have the following values for salary (in thousands of dollars), shown in increasing order: 30, 36, 47, 50, 52, 52, 56, 60, 63, 70, 70, 110.
- 20. • Trimmed mean • Even a small number of extreme values can corrupt the mean. • For example, the mean salary at a company may be substantially pushed up by that of a few highly paid managers. • Similarly, the mean score of a class in an exam could be pulled down quite a bit by a few very low scores. • To offset the effect caused by a small number of extreme values, we can instead use the trimmed mean
- 21. • Median. Suppose we have the following values for salary (in thousands of dollars), shown in increasing order: 30, 36, 47, 50, 52, 52, 56, 60, 63, 70, 70, 110) • The data are already sorted in increasing order. There is an even number of observations (i.e., 12); • therefore, the median is not unique. • It can be any value within the two middlemost values of 52 and 56 (that is, within the sixth and seventh values in the list). • By convention, we assign the average of the two middlemost values as the median; that is, • (52+56 )/2 = 108 /2 = 54. Thus, the median is $54,000
- 22. • Suppose that we had only the first 11 values in the list. Given an odd number of values, the median is the middlemost value. This is the sixth value in this list, which has a value of $52,000. • The median is expensive to compute when we have a large number of observations.
- 23. where L1 is the lower boundary of the median interval, n is the number of values in the entire data set, Freqmedian is the frequency of the median interval, and width is the width of the median interval. is the sum of the frequencies of all of the intervals
- 24. • Mode : Suppose we have the following values for salary (in thousands of dollars), shown in increasing order: 30, 36, 47, 50, 52, 52, 56, 60, 63, 70, 70, 110) • The two modes are $52,000 and $70,000. • The mode for a set of data is the value that occurs most frequently in the set. • Therefore, it can be determined for qualitative and quantitative attributes • Data sets with one, two, or three modes are respectively called unimodal, bimodal, and trimodal. In general, a data set with two or more modes is multimodal.
- 25. • For unimodal numeric data that are moderately skewed (asymmetrical), • we have the following empirical relation: mean − mode ≈ 3 × (mean − median). • This implies that the mode for unimodal frequency curves that are moderately skewed can easily be approximated if the mean and median values are known. • The midrange can also be used to assess the central tendency of a numeric data set. • It is the average of the largest and smallest values in the set
- 26. • Suppose we have the following values for salary (in thousands of dollars), shown in increasing order: 30, 36, 47, 50, 52, 52, 56, 60, 63, 70, 70, 110) • Midrange. The midrange of the data of Example 2.6 is 30,000+110,000 2 = $70,000. • In a unimodal frequency curve with perfect symmetric data distribution, the mean, median, and mode are all at the same center value, as shown in Figure 2.1(a). • Data in most real applications are not symmetric. They may instead be either positively skewed, where the mode occurs at a value that is smaller than the median (Figure 2.1b), • or negatively skewed, where the mode occurs at a value greater than the median (Figure 2.1c).
- 29. Skewness • Skewness is used to measure symmetry of data along with the mean value. Symmetry means equal distribution of observation above or below the mean. • skewness = 0: if data is symmetric along with mean • skewness = Negative: if data is not symmetric and right side tail is longer than left side tail of density plot. • skewness = Positive: if data is not symmetric and left side tail is longer than right side tail in density plot. • We can find skewness of given variable by below given formula. • data[‘A’].skew()
- 30. • In a unimodal frequency curve with perfect symmetric data distribution, the mean, median, and mode are all at the same center value, as shown in Figure 2.1(a).
- 31. • Data in most real applications are not symmetric. • They may instead be either positively skewed, where the mode occurs at a value that is smaller than the median (Figure 2.1b), • negatively skewed, where the mode occurs at a value greater than the median (Figure 2.1c).
- 32. Range, Quartiles, and Interquartile Range
- 34. Range, Quartiles, and Interquartile Range • Let x1,x2,...,xN be a set of observations for some numeric attribute, X. • The range of the set is the difference between the largest (max()) and smallest (min()) values
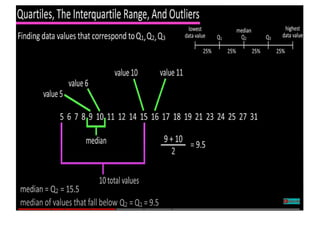
- 37. • Suppose that the data for attribute X are sorted in increasing numeric order. Imagine that we can pick certain data points so as to split the data distribution into equal-size consecutive sets, as in Figure
- 48. Examples • 75, 69, 56, 46, 47, 79, 92, 97, 89, 88, 36, 96, 105, 32, 116, 101, 79, 93, 91, 112 • After sorting the above data set: 32, 36, 46, 47, 56, 69, 75, 79, 79, 88, 89, 91, 92, 93, 96, 97, 101, 105, 112, 116 • Here the total number of terms is 20. • The second quartile (Q2) or the median of the above data is (88 + 89) / 2 = 88.5 • The first quartile (Q1) is median of first n i.e. 10 terms (or n i.e. 10 smallest values) = 62.5 • The third quartile (Q3) is the median of n i.e. 10 largest values (or last n i.e. 10 values) = 96.5 • Then, IQR = Q3 – Q1 = 96.5 – 62.5 = 34.0
- 50. • The IQR is used to build box plots, simple graphical representations of a probability distribution. • The IQR can also be used to identify the outliers in the given data set. • The IQR gives the central tendency of the data. Decision Making • The data set has a higher value of interquartile range (IQR) has more variability. • The data set having a lower value of interquartile range (IQR) is preferable. • Suppose if we have two data sets and their interquartile ranges are IR1 and IR2, and if IR1 > IR2 then the data in IR1 is said to have more variability than the data in IR2 and data in IR2 is preferable. USE of IQR
- 51. Variance and Standard Deviation • Variance and standard deviation are measures of data dispersion. • They indicate how spread out a data distribution is. • A low standard deviation means that the data observations tend to be very close to the mean, while a high standard deviation indicates that the data are spread out over a large range of values.