BINARY TREE REPRESENTATION.ppt

TREES-BINARY TREE
REPRESENTATION
B Y
D . S E E T H A L A K S H M I
A S S I S TA N T P R O F E S S O R
D E PA R T M E N T O F C O M P U T E R
A P P L I C AT I O N S
B O N S E C O U R S C O L L E G E F O R
W O M E N

NON-LINEAR DATA STRUCTURE
• These data structures donot have their
elements in a sequence.
• Trees is an example.
• Trees are mainly used to represent data
containing a hierarchical relationship
between elements, ex : records, family
trees and table of contents.

TERMINOLOGY OF TREES
• The boxes on the tree are called nodes
• The nodes immediately below (to the left and right of) a given node
are called its children
• The node immediately above a given node is called its parent
• The (unique) node without a parent is called the root
• A node with no children is called a leaf
• Two children of the same parent are said to be siblings
• A node can be an ancestor (e.g. grandparent) or a descendant
(e.g. great-grandchild)

SOME TREE TERMINOLOGY
• root: node with no parent
– A non-empty tree has exactly one root
• leaf: node with no children
• siblings: two nodes with the same parent.
• path: a sequence of nodes n1, n2, … , nk such that ni is the parent of
ni+1 for 1  i < k
– in other words, a sequence of hops to get from one node to
another
– the length of a path is the number of edges in the path, or 1 less
than the number of nodes in it

DEPTH AND HEIGHT
• depth or level: length of the path from root to the current node
(depth of root = 0)
• height: length of the longest path from root to any leaf
– empty (null) tree's height: -1
– single-element tree's height: 0
– tree with a root with children: 1

TREES
• Tree nodes contain two or more links
– All other data structures we have
discussed only contain one
• Binary trees
– All nodes contain two links
• None, one, or both of which may be NULL
– The root node is the first node in a tree.
– Each link in the root node refers to a child
– A node with no children is called a leaf node

BINARY TREES
• Special type of tree in which every node or
vertex has either no children, one child or
two children.
• Characteristics :
• Every binary tree has a root pointer which
points to the start of the tree.
• A binary tree can be empty.
• It consists of a node called root, a left subtree
and right subtree both of which are binary
trees themselves.

EXAMPLES : BINARY TREES
X X
Y Y
Z
(2) (3)
X X
Z
A
B C
(1) (4)
Root of tree is node having info as X.
(1) Only node is root.
(2) Root has left child Y.
(3) Root X has right child Z.
(4) Root X has left child Y and right child Z which
is again a binary tree with its parent as Z and
left child of Z is A, which in turn is parent for
left child B and right child C.

PROPERTIES OF BINARY TREE
• A tree with n nodes has exactly (n-1) edges or
branches.
• In a tree every node except the root has exactly
one parent (and the root node does not have a
parent).
• There is exactly one path connecting any two
nodes in a tree.
• The maximum number of nodes in a binary tree
of height K is 2K+1 -1 where K>=0.

REPRESENTATION OF BINARY TREE
• Array representation
– The root of the tree is
stored in position 0.
– The node in position p, is
the implicit father of nodes
2p+1 and 2p+2.
– Left child is at 2p+1 and
right at 2p+2.
X
Y Z
A
B
0 1 2 3 4 5 6 7 8 10
C
11 12
X Y Z A B C
9

REPRESENTATION OF BINARY TREE
• Linked List
• Every node will consists of information, and two
pointers left and right pointing to the left and right
child nodes.
struct node
{
int data;
struct node *left; struct node *right;
};
• The topmost node or first node is pointed by a root
pointer which will inform the start of the tree. Rest of
the nodes are attached either to left if less than parent
or right if more or equal to parent.

• Diagram of a binary tree
B
A D
C

OPERATIONS ON BINARY TREE
• Searching an existing node.
• Inserting a new node.
• Deleting an existing node.
• Traversing the tree.
• Preorder
• Inorder
• Postorder

SEARCH PROCESS
• Initialize a search pointer as the root pointer.
• All the data is compared with the data stored in each
node of the tree starting from root node.
• If the data to be searched is equal to the data of the
node then print “successful” search.
• Else if the data is less than node’s data move the pointer
to left subtree. Else data is more than node’s data move
the pointer to right subtree.
• Keep moving in the tree until the data is found or search
pointer comes to NULL in which case it is an
“unsuccessful” search.

EXAMPLE USED FOR SEARCH
21
18
19
7
6 9
8 11
14
13
Root

EXAMPLE : SEARCH
• Initialize temp as root pointer which is node having 21.
• Loop until temp!=NULL or ITEM found
• Compare item=9 with the root 21 of the tree, since
9<21, proceed temp to the left child of the tree.
• Compare ITEM=9 with 18 since 9<18 proceed temp
to the left subtree of 18, which is 7.
• Compare ITEM=9 with 7 since 9>7 proceed temp to
right subtree of the node which holds a value 7.
• Now ITEM=9 is compared with the node which holds
value 9 and since 9 is found the searching process
ens here.

INSERT PROCESS
• For node insertion in a binary search tree, initially the
data that is to be inserted is compared with the data of
the root data.
• If the data is found to be greater than or equal to the
data of the root node then the new node is inserted in
the right subtree of the root node, else left subtree.
• Now the parent of the right or left subtree is considered
and its data is compared with the data of the new node
and the same procedure is repeated again until a NULL
is found which will indicate a space when the new node
has to be attached. Thus finally the new node is made
the appropriate child of this current node.

EXAMPLE USED FOR INSERT
38
14
23
8
Root
56
82
45
18 70
20

EXAMPLE : INSERT
• Suppose the ITEM=20 is the data part of the new node
to be inserted in the tree and the root is pointing to the
start of the tree.
• Compare ITEM=20 with the root 38 of the tree. Since 20
< 38 proceed to the left child of 38, which is 14.
• Compare ITEM=20 with 14, since 20 > 14 proceed to the
right child of 14, which is 23.
• Compare ITEM=20 with 23 since 20 < 23 proceed to the
left child of 23 which is 18.
• Compare ITEM=20 with 18 since 20 > 18 and 18 does
not have right child, 10 is inserted as the right child of 18.

• Tree traversals:
– Inorder traversal – prints the node values in ascending order
1. Traverse the left subtree with an inorder traversal
2. Process the value in the node (i.e., print the node value)
3. Traverse the right subtree with an inorder traversal
– Preorder traversal
1. Process the value in the node
2. Traverse the left subtree with a preorder traversal
3. Traverse the right subtree with a preorder traversal
– Postorder traversal
1. Traverse the left subtree with a postorder traversal
2. Traverse the right subtree with a postorder traversal
3. Process the value in the node

BINARY TREE TRAVERSALS
• three common binary tree traversal orderings (each one begins at
the root):
– preorder traversal: the current node is processed, then the
node's left subtree is traversed, then the node's right subtree is
traversed (CURRENT-LEFT-RIGHT)
– in-order traversal: the node's left subtree is traversed, then the
current node itself is processed, then the node's right subtree is
traversed (LEFT-CURRENT-RIGHT)
– postorder traversal: the node's left subtree is traversed, then
the node's right subtree is traversed, and lastly the current node
is processed (LEFT-RIGHT-CURRENT)

BINARY TREE PREORDER
TRAVERSAL
"G"
"F"
• order: C F T B R K G
– The trick: Walk around the outside of the tree and emit a node's
value when you touch the left side of the node.
root
"C"
"T"
"R"
"B"
"K"

BINARY TREE IN-ORDER TRAVERSAL
order: B T R F K C G
– The trick: Walk around the outside of the tree and emit a node's value
when you touch the bottom side of the node.
root
"C"
"F"
"T"
"G"
"R"
"B"
"K"

BINARY TREE POSTORDER
TRAVERSAL
order: B R T K F G C
– The trick: Walk around the outside of the tree and emit a node's value
when you touch the right side of the node
root
"C"
"F"
"T" "G"
"R"
"B"
"K"

DELETE PROCESS
• There are four possible conditions are to be taken into account :
i. No node in the tree holds the specified data.
ii. The node containing the data has no children.
iii. The node containing the data has exactly one child.
iv. The node containing data has two children.
• Condition (i) In this case we simply print the message that the data
item is not present in the tree.
• Condition (ii) In this case since the node to be deleted has no
children the memory occupied by this should be freed and either
the left link or the right link of the parent of this node should be set
to NULL. Which of these is to be set to NULL depends upon
whether the node being deleted is a left child or right child of its
parent.

CONDITION (III)
• In this case since the node to be deleted has one child the solution is to
adjust the pointer of the parent of the node to be deleted such that after
deletion it points to the child of the node being deleted as in the diagram.
18
19
7
6 9
11
10
24
26
25 30
21 21
18
19
7
6 11
10
24
26
25 30
Root Root

CONDITION (IV)
In this case the node to be deleted has two children. Consider node 9 before deletion. The inorder successor of the
node 9 is node 10. The data of this inorder successor should now be copied into the node to be deleted and a pointer
should be set up pointing to the inorder successor (node 10). This inorder successor would always have one or zero
child. It should then be deleted using the same procedure as for deleting one child or a zero child node. Thus, the whole
logic of deleting a node with two children is to locate the inorder successor, copy its data and reduce the problem to a
simple deletion of a node with one or zero child. This is shown in the example.
18
19
7
6 9
11
10
24
26
25 30
8
21 21
18
19
7
6 10
11
Root Root
24
26
25 30
8
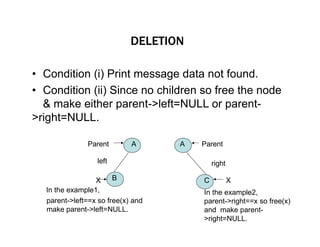
Inorder successor of node 9

DELETION
• Condition (i) Print message data not found.
• Condition (ii) Since no children so free the node
& make either parent->left=NULL or parent-
>right=NULL.
A A
B
Parent Parent
left right
C X
In the example2,
parent->right==x so free(x)
and make parent-
>right=NULL.
X
In the example1,
parent->left==x so free(x) and
make parent->left=NULL.

DELETION
• Condition (iii) Adjust parent to point to the child of the deleted node.
Node deleted(X) has only left child :
If(parent->left==x) parent->left=x->left. If(parent->right==x) parent-
>right=x->left.
I.
1)
2)
A A
B
Parent Parent
left right
X
B
C C
X
left
right

DELETION
• Condition (iii) Adjust parent to point to the child of the deleted node.
Node deleted(X) has only right child :
If(parent->left==x) parent->left=x->right. If(parent->right==x) parent-
>right=x->right.
II.
1)
2)
A A
B
Parent Parent
left right
X B
C C
right
X
right

DELETION
• Condition (iv) solution more complex as X has two children,
• Find inorder successor of the node X. Inorder successor of any node will be first go to right of the
node and then from that node keep going left until NULL encountered, that will be the inorder
successor.
• Copy data of inorder successor to node X’s data.
• Place pointer at the inorder successor node. Now the inorder succesor will have zero or one child
only (so the complex problem is reduced to condition (iii)).
• Delete the inorder successor node by using logic of condition (ii) if no children or condition (iiii) if one
right child.
B
Parent A
left
D
right
X
left
C
left
E
E
Parent A
left
D
right
X
left
C
left
E
Here inorder successor E has
no children condition (ii)

DELETION
Parent
X
left
C
left
B
left
E
right
left
G
A
right D
Inorder
Successor
F
right H
Parent
left C
X
left
E
left
E
right
left
G
A
right D
Inorder
Successor
F
right H
Parent A left
E
left right
C D
left
F
left right
G H
Here inorder successor E has
one right child condition (iii)
If(parent->left==x)
parent->left=x->right.

APPLICATION OF TREE
• Expression Tree
• Game Tree

BINARY TREE REPRESENTATION.ppt

More Related Content

What's hot (20)

Similar to BINARY TREE REPRESENTATION.ppt (20)

More from SeethaDinesh (20)

Recently uploaded (20)

BINARY TREE REPRESENTATION.ppt