Brief Introduction to Deep Learning + Solving XOR using ANNs
15 likes8,021 views
The document introduces deep learning and demonstrates solving the XOR problem using artificial neural networks (ANN). It includes technical details about neural network architecture such as input, hidden, and output layers, as well as the use of activation functions. The document also discusses weight adjustments and classifications involved in the neural network process.
![Regarding 5th Step: Weights Adaptation
• If the predicted output Y is not the same as the desired output d,
then weights are to be adapted according to the following equation:
𝑾 𝒏 + 𝟏 = 𝑾 𝒏 + η 𝒅 𝒏 − 𝒀 𝒏 𝑿(𝒏)
Where
𝑾 𝒏 = [𝒃 𝒏 , 𝑾 𝟏(𝒏), 𝑾 𝟐(𝒏), 𝑾 𝟑(𝒏), … , 𝑾 𝒎(𝒏)]](https://image.slidesharecdn.com/briefintroductiontodeeplearningsolvingxorusingann-shared-170723215849/85/Brief-Introduction-to-Deep-Learning-Solving-XOR-using-ANNs-84-320.jpg)
Brief Introduction to Deep Learning + Solving XOR using ANNs
- 1. Brief Introduction to Deep Learning + Solving XOR using ANN MENOUFIA UNIVERSITY FACULTY OF COMPUTERS AND INFORMATION المنوفية جامعة الحاسبات كليةوالمعلومات المنوفية جامعة Ahmed Fawzy Gad [email protected]
- 3. Neural Networks Input Hidden Output BA 01 1 10 00 0 11
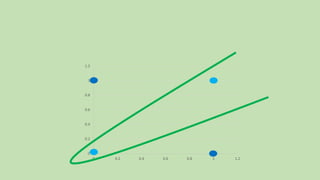
- 4. Neural Networks BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2
- 5. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2
- 6. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2
- 7. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2
- 8. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2
- 9. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2
- 10. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2
- 11. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2
- 12. = +0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5
- 13. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Network Architecture!!
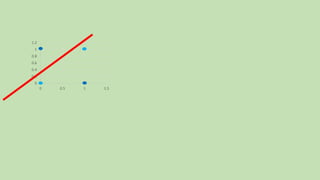
- 14. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 = + 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5
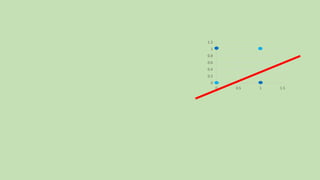
- 15. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5
- 16. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5
- 17. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 Input OutputHidden
- 18. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 Input OutputHidden
- 19. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 Input OutputHidden
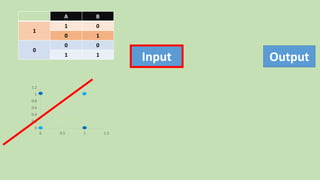
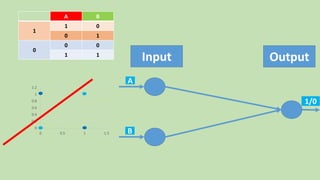
- 20. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 BA 01 1 10 00 0 11 Input Output
- 21. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 BA 01 1 10 00 0 11 Input Output
- 22. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 BA 01 1 10 00 0 11 Input Output
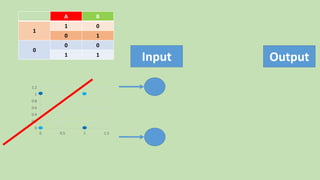
- 23. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 BA 01 1 10 00 0 11 Input Output A B
- 24. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 BA 01 1 10 00 0 11 Input Output A B
- 25. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 BA 01 1 10 00 0 11 Input Output A B
- 26. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 BA 01 1 10 00 0 11 Input Output A B
- 27. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 BA 01 1 10 00 0 11 Input Output A B 1/0
- 28. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 Input Output A B 1/0 𝑾 𝟏 𝑾 𝟐
- 29. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 = + 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5
- 30. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5
- 31. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5
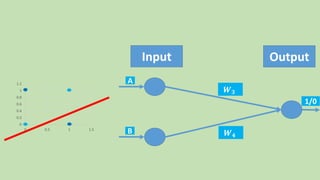
- 32. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 Input Output A B 1/0 𝑾 𝟑 𝑾 𝟒
- 33. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 A B 1/0 𝑾 𝟑 𝑾 𝟒 A B 1/0 𝑾 𝟏 𝑾 𝟐 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5
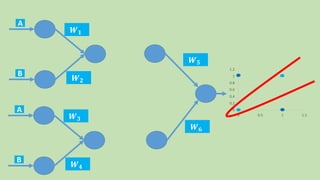
- 34. 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 A B 𝑾 𝟑 𝑾 𝟒
- 35. A B 𝑾 𝟏 𝑾 𝟐 A B 𝑾 𝟑 𝑾 𝟒 𝑾 𝟓 𝑾 𝟔
- 36. 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 A B 𝑾 𝟑 𝑾 𝟒 𝑾 𝟓 𝑾 𝟔 A 𝑾 𝟏 𝑾 𝟐 B 𝑾 𝟑 𝑾 𝟒
- 37. 𝑾 𝟓 𝑾 𝟔 A 𝑾 𝟏 𝑾 𝟐 B 𝑾 𝟑 𝑾 𝟒
- 39. . . . . . .
- 40. . . .
- 41. . . . . . .
- 42. . . .
- 43. . . . . . .
- 44. . . . . . .
- 45. . . .
- 46. . . .
- 52. Input Output BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Hidden Weights=𝑾𝒊 𝑾 𝟓 𝑾 𝟔 1/0 𝒀𝒋 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
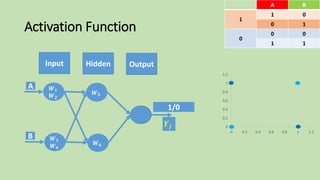
- 53. Activation Function Output 𝒀𝒋 BA 01 1 10 00 0 11 Input Hidden 1/0 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 54. Activation Function Output 𝒀𝒋 BA 01 1 10 00 0 11 Input Hidden 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 1/0 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 55. Activation Function Output 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 1/0 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 56. Activation Function Components Output 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 1/0 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 57. Activation Function Inputs Output s 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 1/0 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 58. Activation Function Inputs Output s 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 1/0 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒 s=SOP(𝑿𝒊, 𝑾𝒊)
- 59. Activation Function Inputs Output s 𝑿𝒊=Inputs 𝑾𝒊=Weights 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 1/0 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒 s=SOP(𝑿𝒊, 𝑾𝒊)
- 60. Activation Function Inputs Output s 𝑿𝒊=Inputs 𝑾𝒊=Weights 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 1/0 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒 s=SOP(𝑿𝒊, 𝑾𝒊)
- 61. 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒 Activation Function Inputs Output s 𝑿𝒊=Inputs 𝑾𝒊=Weights 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden S= 𝟏 𝒎 𝑿𝒊 𝑾𝒊 s=SOP(𝑿𝒊, 𝑾𝒊) 1/0
- 62. Activation Function Inputs Output s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒 S= 𝟏 𝒎 𝑿𝒊 𝑾𝒊 1/0 Each Hidden/Output Layer Neuron has its SOP.
- 63. Activation Function Inputs Output s 𝑿 𝟏 𝑿 𝟐 𝑺 𝟏=(𝑿 𝟏 𝑾 𝟏+𝑿 𝟐 𝑾 𝟑) 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒 S= 𝟏 𝒎 𝑿𝒊 𝑾𝒊 1/0
- 64. Activation Function Inputs Output s 𝑿 𝟏 𝑿 𝟐 𝑺 𝟐=(𝑿 𝟏 𝑾 𝟐+𝑿 𝟐 𝑾 𝟒) 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒 S= 𝟏 𝒎 𝑿𝒊 𝑾𝒊 1/0
- 65. Activation Function Inputs Output s 𝑿 𝟏 𝑿 𝟐 𝑺 𝟑=(𝑺 𝟏 𝑾 𝟓+𝑺 𝟐 𝑾 𝟔) 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒 S= 𝟏 𝒎 𝑿𝒊 𝑾𝒊 1/0
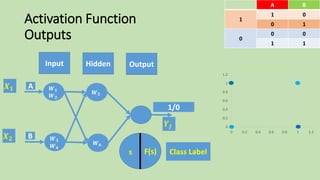
- 66. Activation Function Outputs Output F(s)s 𝑿 𝟏 𝑿 𝟐 Class Label 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 1/0 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 67. Activation Function Outputs Output F(s)s 𝑿 𝟏 𝑿 𝟐 Class Label 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 Input Hidden 1/0 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
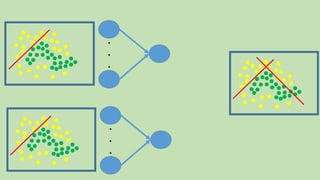
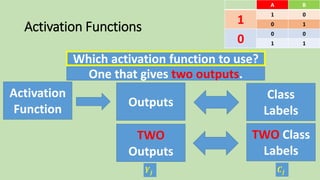
- 69. Activation Functions Which activation function to use? Outputs Class Labels Activation Function TWO Class Labels TWO Outputs One that gives two outputs. Which activation function to use? 𝑪𝒋𝒀𝒋 BA 01 1 10 00 0 11 BA 01 1 10 00 0 11
- 70. Activation Functions Piecewise Linear Sigmoid BinaryBinary
- 71. Activation Function Output F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 BA 01 1 10 00 0 11 0 0.2 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 0.8 1 1.2 1/0 Input Hidden 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 72. Bias Input Output BA 01 1 10 00 0 11 F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 1/0 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
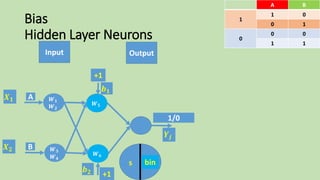
- 73. Bias Hidden Layer Neurons Input Output BA 01 1 10 00 0 11 F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒 +1 𝒃 𝟏 +1 𝒃 𝟐 1/0
- 74. Bias Output Layer Neurons Input Output BA 01 1 10 00 0 11 F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 +1 𝒃 𝟑 1/0 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 75. All Bias Values Input Output BA 01 1 10 00 0 11 F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 +1 𝒃 𝟏 +1 𝒃 𝟐 1/0 +1 𝒃 𝟑 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
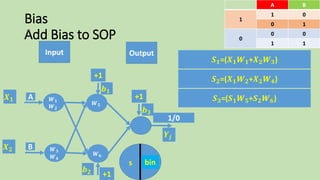
- 76. Bias Add Bias to SOP Input Output BA 01 1 10 00 0 11 F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 +1 𝒃 𝟏 +1 𝒃 𝟐 𝑺 𝟏=(𝑿 𝟏 𝑾 𝟏+𝑿 𝟐 𝑾 𝟑) 𝑺 𝟐=(𝑿 𝟏 𝑾 𝟐+𝑿 𝟐 𝑾 𝟒) 𝑺 𝟑=(𝑺 𝟏 𝑾 𝟓+𝑺 𝟐 𝑾 𝟔) 1/0 +1 𝒃 𝟑 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 77. Bias Add Bias to SOP Input Output BA 01 1 10 00 0 11 F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 +1 𝒃 𝟏 +1 𝒃 𝟐 𝑺 𝟏=(𝑿 𝟏 𝑾 𝟏+𝑿 𝟐 𝑾 𝟑) 1/0 +1 𝒃 𝟑 𝑺 𝟏=(+𝟏𝒃 𝟏+𝑿 𝟏 𝑾 𝟏+𝑿 𝟐 𝑾 𝟑) 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 78. Bias Add Bias to SOP Input Output BA 01 1 10 00 0 11 F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 +1 𝒃 𝟏 +1 𝒃 𝟐 𝑺 𝟐=(𝑿 𝟏 𝑾 𝟐+𝑿 𝟐 𝑾 𝟒) 1/0 +1 𝒃 𝟑 𝑺 𝟐=(+𝟏𝒃 𝟐+𝑿 𝟏 𝑾 𝟐+𝑿 𝟐 𝑾 𝟒) 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 79. Bias Add Bias to SOP Input Output BA 01 1 10 00 0 11 F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 +1 𝒃 𝟏 +1 𝒃 𝟐 𝑺 𝟑=(𝑺 𝟏 𝑾 𝟓+𝑺 𝟐 𝑾 𝟔) 1/0 +1 𝒃 𝟑 𝑺 𝟑=(+𝟏𝒃 𝟑+𝑺 𝟏 𝑾 𝟓+𝑺 𝟐 𝑾 𝟔) 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
- 80. Learning Rate 𝟎 ≤ η ≤ 𝟏 F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 +1 𝒃 𝟏 +1 𝒃 𝟐 1/0 +1 𝒃 𝟑 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒
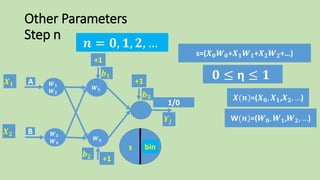
- 81. Other Parameters Step n 𝒏 = 𝟎, 𝟏, 𝟐, … F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 +1 𝒃 𝟏 +1 𝒃 𝟐 1/0 +1 𝒃 𝟑 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒 s=(𝑿 𝟎 𝑾 𝟎+𝑿 𝟏 𝑾 𝟏+𝑿 𝟐 𝑾 𝟐+…) 𝟎 ≤ η ≤ 𝟏 𝑿(𝒏)=(𝑿 𝟎, 𝑿 𝟏,𝑿 𝟐, …) W(𝒏)=(𝑾 𝟎, 𝑾 𝟏,𝑾 𝟐, …)
- 82. Other Parameters Desired Output 𝒅𝒋 𝒏 = 𝟎, 𝟏, 𝟐, … 𝒅 𝒏 = 𝟏, 𝒙 𝒏 𝒃𝒆𝒍𝒐𝒏𝒈𝒔 𝒕𝒐 𝑪𝟏 (𝟏) 𝟎, 𝒙 𝒏 𝒃𝒆𝒍𝒐𝒏𝒈𝒔 𝒕𝒐 𝑪𝟐 (𝟎) BA 01 1 10 00 0 11 F(s)s 𝑿 𝟏 𝑿 𝟐 bin 𝒀𝒋 +1 𝒃 𝟏 +1 𝒃 𝟐 1/0 +1 𝒃 𝟑 𝑾 𝟓 𝑾 𝟔 A B 𝑾 𝟏 𝑾 𝟐 𝑾 𝟑 𝑾 𝟒 s=(𝑿 𝟎 𝑾 𝟎+𝑿 𝟏 𝑾 𝟏+𝑿 𝟐 𝑾 𝟐+…) 𝟎 ≤ η ≤ 𝟏 𝑿(𝒏)=(𝑿 𝟎, 𝑿 𝟏,𝑿 𝟐, …) W(𝒏)=(𝑾 𝟎, 𝑾 𝟏,𝑾 𝟐, …)
- 83. Neural Networks Training Steps Weights Initialization Inputs Application Sum of Inputs-Weights Products Activation Function Response Calculation Weights Adaptation Back to Step 2 1 2 3 4 5 6
- 84. Regarding 5th Step: Weights Adaptation • If the predicted output Y is not the same as the desired output d, then weights are to be adapted according to the following equation: 𝑾 𝒏 + 𝟏 = 𝑾 𝒏 + η 𝒅 𝒏 − 𝒀 𝒏 𝑿(𝒏) Where 𝑾 𝒏 = [𝒃 𝒏 , 𝑾 𝟏(𝒏), 𝑾 𝟐(𝒏), 𝑾 𝟑(𝒏), … , 𝑾 𝒎(𝒏)]
- 85. Neural Networks Training Example Step n=0 • In each step in the solution, the parameters of the neural network must be known. • Parameters of step n=0: η = .001 𝑋 𝑛 = 𝑋 0 = +1, +1, +1,1, 0 𝑊 𝑛 = 𝑊 0 = 𝑏1, 𝑏2, 𝑏3, 𝑤1, 𝑤2, 𝑤3, 𝑤4, 𝑤5, 𝑤6 = −1.5, −.5, −.5, 1, 1, 1, 1, −2, 1 𝑑 𝑛 = 𝑑 0 = 1 BA 01 1 => 1 10 00 0 => 0 11
- 86. Neural Networks Training Example Step n=0 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin BA 01 1 => 1 10 00 0 => 0 11
- 87. Neural Networks Training Example Step n=0 – SOP – 𝑺 𝟏 𝑺 𝟏=(+𝟏𝒃 𝟏+𝑿 𝟏 𝑾 𝟏+𝑿 𝟐 𝑾 𝟑) =+1*-1.5+1*1+0*1 =-.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 88. Neural Networks Training Example Step n=0 – Output – 𝑺 𝟏 𝒀 𝑺 𝟏 = = 𝑩𝑰𝑵 𝑺 𝟏 = 𝑩𝑰𝑵 −. 𝟓 = 𝟎 𝒃𝒊𝒏 𝒔 = +𝟏, 𝒔 ≥ 𝟎 𝟎, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 89. Neural Networks Training Example Step n=0 – SOP – 𝑺 𝟐 𝑺 𝟐=(+𝟏𝒃 𝟐+𝑿 𝟏 𝑾 𝟐+𝑿 𝟐 𝑾 𝟒) =+1*-.5+1*1+0*1 =.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 90. Neural Networks Training Example Step n=0 – Output – 𝑺 𝟐 𝒀 𝑺2 = = 𝑩𝑰𝑵 𝑺2 = 𝑩𝑰𝑵 . 𝟓 = 1 𝒃𝒊𝒏 𝒔 = +𝟏, 𝒔 ≥ 𝟎 −𝟏, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 91. Neural Networks Training Example Step n=0 – SOP – 𝑺 𝟑 𝑺 𝟑=(+𝟏𝒃 𝟑+𝑺 𝟏 𝑾 𝟓+𝑺 𝟐 𝑾 𝟔) =+1*-.5+0*-2+1*1 =.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 92. Neural Networks Training Example Step n=0 – Output – 𝑺 𝟑 𝒀 𝑺3 = = 𝑩𝑰𝑵 𝑺3 = 𝑩𝑰𝑵 . 𝟓 = 1 𝒃𝒊𝒏 𝒔 = +𝟏, 𝒔 ≥ 𝟎 𝟎, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 93. Neural Networks Training Example Step n=0 - Output 𝒀 𝒏 = 𝒀 𝟎 = 𝒀 𝑺3 = 1 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 94. Neural Networks Training Example Step n=0 Predicted Vs. Desired 𝒀 𝒏 = 𝒀 𝟎 = 1 𝐝 𝒏 = 𝒅 𝟎 = 1 ∵ 𝒀 𝒏 = 𝒅 𝒏 ∴ Weights are Correct. No Adaptation BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 95. Neural Networks Training Example Step n=1 • In each step in the solution, the parameters of the neural network must be known. • Parameters of step n=1: η = .001 𝑋 𝑛 = 𝑋 1 = +1, +1, +1,0, 1 𝑊 𝑛 = 𝑊 1 = 𝑊 0 = 𝑏1, 𝑏2, 𝑏3, 𝑤1, 𝑤1, 𝑤2, 𝑤3, 𝑤4, 𝑤5, 𝑤6 = −1.5, −.5, −.5, 1, 1, 1, 1, −2, 1 𝑑 𝑛 = 𝑑 1 = +1 BA 01 1 => 1 10 00 0 => 0 11
- 96. Neural Networks Training Example Step n=1 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin BA 01 1 => 1 10 00 0 => 0 11
- 97. Neural Networks Training Example Step n=1 – SOP – 𝑺 𝟏 𝑺 𝟏=(+𝟏𝒃 𝟏+𝑿 𝟏 𝑾 𝟏+𝑿 𝟐 𝑾 𝟑) =+1*-1.5+0*1+1*1 =-.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 98. Neural Networks Training Example Step n=1 – Output – 𝑺 𝟏 𝒀 𝑺 𝟏 = = 𝑩𝑰𝑵 𝑺 𝟏 = 𝑩𝑰𝑵 −. 𝟓 = 𝟎 𝒃𝒊𝒏 𝒔 = +𝟏, 𝒔 ≥ 𝟎 𝟎, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 99. Neural Networks Training Example Step n=1 – SOP – 𝑺 𝟐 𝑺 𝟐=(+𝟏𝒃 𝟐+𝑿 𝟏 𝑾 𝟐+𝑿 𝟐 𝑾 𝟒) =+1*-.5+0*1+1*1 =.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 100. Neural Networks Training Example Step n=1 – Output – 𝑺 𝟐 𝒀 𝑺2 = = 𝑩𝑰𝑵 𝑺2 = 𝑩𝑰𝑵 . 𝟓 = 1 𝒃𝒊𝒏 𝒔 = +𝟏, 𝒔 ≥ 𝟎 −𝟏, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 101. Neural Networks Training Example Step n=1 – SOP – 𝑺 𝟑 𝑺 𝟑=(+𝟏𝒃 𝟑+𝑺 𝟏 𝑾 𝟓+𝑺 𝟐 𝑾 𝟔) =+1*-.5+0*-2+1*1 =.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 102. Neural Networks Training Example Step n=1 – Output – 𝑺 𝟑 𝒀 𝑺3 = = 𝑩𝑰𝑵 𝑺3 = 𝑩𝑰𝑵 . 𝟓 = 1 𝒃𝒊𝒏 𝒔 = +𝟏, 𝒔 ≥ 𝟎 𝟎, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 103. Neural Networks Training Example Step n=1 - Output 𝒀 𝒏 = 𝒀 𝟏 = 𝒀 𝑺3 = 1 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 104. Neural Networks Training Example Step n=1 Predicted Vs. Desired 𝒀 𝒏 = 𝒀 𝟏 = 1 𝐝 𝒏 = 𝒅 𝟏 = 1 ∵ 𝒀 𝒏 = 𝒅 𝒏 ∴ Weights are Correct. No Adaptation BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −2 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 105. Neural Networks Training Example Step n=2 • In each step in the solution, the parameters of the neural network must be known. • Parameters of step n=2: η = .001 𝑋 𝑛 = 𝑋 2 = +1, +1, +1,0, 0 𝑊 𝑛 = 𝑊 2 = 𝑊 1 = 𝑏1, 𝑏2, 𝑏3, 𝑤1, 𝑤1, 𝑤2, 𝑤3, 𝑤4, 𝑤5, 𝑤6 = −1.5, −.5, −.5, 1, 1, 1, 1, −2, 1 𝑑 𝑛 = 𝑑 2 = 0 BA 01 1 => 1 10 00 0 => 0 11
- 106. Neural Networks Training Example Step n=2 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin BA 01 1 => 1 10 00 0 => 0 11
- 107. Neural Networks Training Example Step n=2 – SOP – 𝑺 𝟏 𝑺 𝟏=(+𝟏𝒃 𝟏+𝑿 𝟏 𝑾 𝟏+𝑿 𝟐 𝑾 𝟑) =+1*-1.5+0*1+0*1 =-1.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 108. Neural Networks Training Example Step n=2 – Output – 𝑺 𝟏 𝒀 𝑺 𝟏 = = 𝑩𝑰𝑵 𝑺 𝟏 = 𝑩𝑰𝑵 −𝟏. 𝟓 = 𝟎 𝒃𝒊n 𝒔 = +𝟏, 𝒔 ≥ 𝟎 𝟎, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
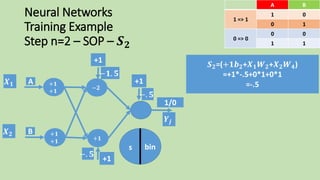
- 109. Neural Networks Training Example Step n=2 – SOP – 𝑺 𝟐 𝑺 𝟐=(+𝟏𝒃 𝟐+𝑿 𝟏 𝑾 𝟐+𝑿 𝟐 𝑾 𝟒) =+1*-.5+0*1+0*1 =-.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 110. Neural Networks Training Example Step n=2 – Output – 𝑺 𝟐 𝒀 𝑺2 = = 𝑺𝑮𝑵 𝑺2 = 𝑺𝑮𝑵 −. 𝟓 =0 𝒃𝒊𝒏 𝒔 = +𝟏, 𝒔 ≥ 𝟎 −𝟏, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 111. Neural Networks Training Example Step n=2 – SOP – 𝑺 𝟑 𝑺 𝟑=(+𝟏𝒃 𝟑+𝑺 𝟏 𝑾 𝟓+𝑺 𝟐 𝑾 𝟔) =+1*-.5+0*-2+0*1 =-.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 112. Neural Networks Training Example Step n=2 – Output – 𝑺 𝟑 𝒀 𝑺3 = = 𝑩𝑰𝑵 𝑺3 = 𝑩𝑰𝑵 −. 𝟓 = 𝟎 𝒃𝒊𝒏 𝒔 = +𝟏, 𝒔 ≥ 𝟎 𝟎, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 113. Neural Networks Training Example Step n=2 - Output 𝒀 𝒏 = 𝒀 𝟐 = 𝒀 𝑺3 = 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 114. Neural Networks Training Example Step n=2 Predicted Vs. Desired 𝒀 𝒏 = 𝒀 𝟐 = 𝟎 𝐝 𝒏 = 𝒅 𝟐 = 𝟎 ∵ 𝒀 𝒏 = 𝒅 𝒏 ∴ Weights are Correct. No Adaptation BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 115. Neural Networks Training Example Step n=3 • In each step in the solution, the parameters of the neural network must be known. • Parameters of step n=3: η = .001 𝑋 𝑛 = 𝑋 3 = +1, +1, +1,1, 1 𝑊 𝑛 = 𝑊 3 = 𝑊 2 = 𝑏1, 𝑏2, 𝑏3, 𝑤1, 𝑤1, 𝑤2, 𝑤3, 𝑤4, 𝑤5, 𝑤6 = −1.5, −.5, −.5, 1, 1, 1, 1, −2, 1 𝑑 𝑛 = 𝑑 3 = 0 BA 01 1 => 1 10 00 0 => 0 11
- 116. Neural Networks Training Example Step n=3 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin BA 01 1 => 1 10 00 0 => 0 11
- 117. Neural Networks Training Example Step n=3 – SOP – 𝑺 𝟏 𝑺 𝟏=(+𝟏𝒃 𝟏+𝑿 𝟏 𝑾 𝟏+𝑿 𝟐 𝑾 𝟑) =+1*-1.5+1*1+1*1 =.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
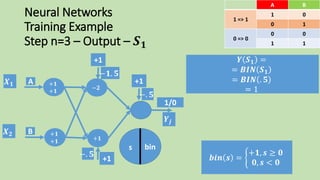
- 118. Neural Networks Training Example Step n=3 – Output – 𝑺 𝟏 𝒀 𝑺 𝟏 = = 𝑩𝑰𝑵 𝑺 𝟏 = 𝑩𝑰𝑵 . 𝟓 = 1 𝒃𝒊𝒏 𝒔 = +𝟏, 𝒔 ≥ 𝟎 𝟎, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 119. Neural Networks Training Example Step n=3 – SOP – 𝑺 𝟐 𝑺 𝟐=(+𝟏𝒃 𝟐+𝑿 𝟏 𝑾 𝟐+𝑿 𝟐 𝑾 𝟒) =+1*-.5+1*1+1*1 =1.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 120. Neural Networks Training Example Step n=3 – Output – 𝑺 𝟐 𝒀 𝑺2 = = 𝑩𝑰𝑵 𝑺2 = 𝑩𝑰𝑵 𝟏. 𝟓 = 1 𝒃𝒊𝒏 𝒔 = +𝟏, 𝒔 ≥ 𝟎 −𝟏, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
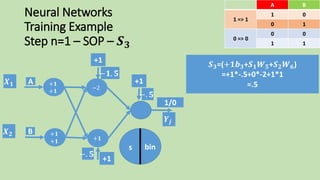
- 121. Neural Networks Training Example Step n=3 – SOP – 𝑺 𝟑 𝑺 𝟑=(+𝟏𝒃 𝟑+𝑺 𝟏 𝑾 𝟓+𝑺 𝟐 𝑾 𝟔) =+1*-.5+1*-2+1*1 =-1.5 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 122. Neural Networks Training Example Step n=3 – Output – 𝑺 𝟑 𝒀 𝑺3 = = 𝑩𝑰𝑵 𝑺3 = 𝑩𝑰𝑵 −𝟏. 𝟓 = 𝟎 𝒃𝒊𝒏 𝒔 = +𝟏, 𝒔 ≥ 𝟎 𝟎, 𝒔 < 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 123. Neural Networks Training Example Step n=3 - Output 𝒀 𝒏 = 𝒀 𝟑 = 𝒀 𝑺3 = 𝟎 BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 124. Neural Networks Training Example Step n=3 Predicted Vs. Desired 𝒀 𝒏 = 𝒀 𝟑 = 𝟎 𝐝 𝒏 = 𝒅 𝟑 = 𝟎 ∵ 𝒀 𝒏 = 𝒅 𝒏 ∴ Weights are Correct. No Adaptation BA 01 1 => 1 10 00 0 => 0 11 s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin
- 125. Final Weights s 𝑿 𝟏 𝑿 𝟐 𝒀𝒋 +1 −𝟏. 𝟓 +1 −. 𝟓 1/0 +1 −. 𝟓 −𝟐 +𝟏 A B +𝟏 +𝟏 +𝟏 +𝟏 bin Current weights predicted the desired outputs.