C Language Unit-8

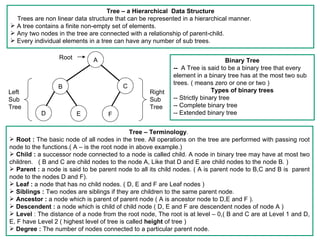
Tree – a Hierarchical Data Structure
Trees are non linear data structure that can be represented in a hierarchical manner.
 A tree contains a finite non-empty set of elements.
 Any two nodes in the tree are connected with a relationship of parent-child.
 Every individual elements in a tree can have any number of sub trees.

Root A Binary Tree
-- A Tree is said to be a binary tree that every
element in a binary tree has at the most two sub
trees. ( means zero or one or two )
B C
Left Right Types of binary trees
Sub Sub -- Strictly binary tree
Tree Tree -- Complete binary tree
D E F -- Extended binary tree

Tree – Terminology.
 Root : The basic node of all nodes in the tree. All operations on the tree are performed with passing root
node to the functions.( A – is the root node in above example.)
 Child : a successor node connected to a node is called child. A node in binary tree may have at most two
children. ( B and C are child nodes to the node A, Like that D and E are child nodes to the node B. )
 Parent : a node is said to be parent node to all its child nodes. ( A is parent node to B,C and B is parent
node to the nodes D and F).
 Leaf : a node that has no child nodes. ( D, E and F are Leaf nodes )
 Siblings : Two nodes are siblings if they are children to the same parent node.
 Ancestor : a node which is parent of parent node ( A is ancestor node to D,E and F ).
 Descendent : a node which is child of child node ( D, E and F are descendent nodes of node A )
 Level : The distance of a node from the root node, The root is at level – 0,( B and C are at Level 1 and D,
E, F have Level 2 ( highest level of tree is called height of tree )
 Degree : The number of nodes connected to a particular parent node.

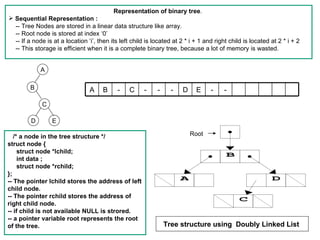
Representation of binary tree.
 Sequential Representation :
-- Tree Nodes are stored in a linear data structure like array.
-- Root node is stored at index ‘0’
-- If a node is at a location ‘i’, then its left child is located at 2 * i + 1 and right child is located at 2 * i + 2
-- This storage is efficient when it is a complete binary tree, because a lot of memory is wasted.

A

B A B - C - - - D E - -

C

D E

/* a node in the tree structure */ Root
struct node {
struct node *lchild;
B
int data ;
struct node *rchild;
};
-- The pointer lchild stores the address of left A D
child node.
-- The pointer rchild stores the address of C
right child node.
-- if child is not available NULL is strored.
-- a pointer variable root represents the root
of the tree. Tree structure using Doubly Linked List

Implementing Binary Tree
struct node { void postorder(struct node *r){
struct node *lchild; if(r!=NULL) {
char data; postorder(r->lchild);
struct node *rchild; postorder(r->rchild);
} *root=NULL; printf("%5c",r->data);
struct node *insert(char a[],int index) { }
struct node *temp=NULL; }
if(a[index]!='0') { void main()
temp = (struct node *)malloc( {
sizeof(struct node)); char arr[] = { 'A','B','C','D','E','F','G','0','0','H','0',
temp->lchild = insert(a,2*index+1); '0','0','0','0','0','0','0','0','0','0'};
temp->data = a[index]; buildtree(arr);
temp->rchild = insert(a,2*index+2); printf("nPre-order Traversal : n");
} preorder(root);
return temp; printf("nIn-order Traversal : n");
} inorder(root);
void buildtree(char a[]) { printf("nIn-order Traversal : n");
root = insert(a,0); inorder(root);
} }
void inorder(struct node *r){
if(r!=NULL) {
inorder(r->lchild); A
printf("%5c",r->data); Tree Created : B C
inorder(r->rchild);
} D E F G
}
void preorder(struct node *r){ H
if(r!=NULL) {
printf("%5c",r->data);
Output :
preorder(r->lchild);
Preorder Traversal : A B D E H C F G
preorder(r->rchild);
} Inorder Traversal : D B H E A F C G
} Postorder Traversal : D H E B F G C A

Binary Search Tree
Binary search tree
– Values in left subtree less than parent
– Values in right subtree greater than parent
– Facilitates duplicate elimination
– Fast searches - for a balanced tree, maximum of log n comparisons
-- Inorder traversal – prints the node values in ascending order

Tree traversals:
Inorder traversal – prints the node values in ascending order
1. Traverse the left subtree with an inorder traversal
2. Process the value in the node (i.e., print the node value)
3. Traverse the right subtree with an inorder traversal
Preorder traversal
1. Process the value in the node
2. Traverse the left subtree with a preorder traversal
3. Traverse the right subtree with a preorder traversal
Postorder traversal
1. Traverse the left subtree with a postorder traversal
2. Traverse the right subtree with a postorder traversal
3. Process the value in the node

Traversals of Tree
 In Order Traversal ( Left – Origin – Right ): 2 3 4 6 7 9 13 15 17 18 20
 Pre Order Traversal ( Origin – Left – Right ) : 15 6 3 2 4 7 13 9 18 17 20
 Post Order Traversal ( Left – Right – Origin ) : 2 4 3 9 13 7 6 17 20 18 15

Implementing Binary Search Tree
struct node { preorder(t->lchild);
struct node *lchild; preorder(t->rchild);
int data; }
struct node *rchild; }
}; void postorder(struct node *t) {
struct node *fnode=NULL,*parent=NULL; if(t!=NULL) {
void insert(struct node **p, int n) { postorder(t->lchild);
if(*p==NULL) { postorder(t->rchild);
*p=(struct node *)malloc(sizeof(struct node)); printf("%5d",t->data);
(*p)->lchild=NULL; }
(*p)->data = n; }
(*p)->rchild=NULL; void search(struct node *r,int key){
return; struct node *q;
} , fnode=NULL; q=r;
if(n < (*p)->data) while(q!=NULL) {
insert(&((*p)->lchild),n); if(q->data == key) {
else fnode = q; return;
insert(&((*p)->rchild),n); }
} parent=q;
void inorder(struct node *t) { if(q->data > key) q=q->lchild;
if(t!=NULL) { else q=q->rchild;
inorder(t->lchild); }
printf("%5d",t->data); }
inorder(t->rchild); void delnode ( struct node **r,int key) {
} struct node *succ,*fnode,*parent;
} if(*r==NULL) {
void preorder(struct node *t) { printf("Tree is empty"); return;
if(t!=NULL) { }
printf("%5d",t->data); parent=fnode=NULL;

Implementing Binary Search Tree ( continued )
search(*r,key); if(fnode->lchild!=NULL && fnode->rchild!=NULL) {
if(fnode==NULL) { parent = fnode;
printf("nNode does not exist, no deletion"); succ = fnode->lchild;
return; while(succ->rchild!=NULL){
} parent=succ;
if(fnode->lchild==NULL && fnode->rchild==NULL) { succ = succ->rchild;
if(parent->lchild==fnode) }
parent->lchild=NULL; fnode->data = succ->data;
else free(succ);
parent->rchild=NULL; succ=NULL;
free(fnode); parent->rchild = NULL;
return; }
} }
if(fnode->lchild==NULL && fnode->rchild!=NULL) { void inorder(struct node *t) {
if(parent->lchild==fnode) if(t!=NULL)
parent->lchild=fnode->rchild; {
else inorder(t->lchild);
parent->rchild=fnode->rchild; printf("%5d",t->data);
free(fnode); inorder(t->rchild);
return; }
} }
if(fnode->lchild!=NULL && fnode->rchild==NULL) { void preorder(struct node *t)
if(parent->lchild==fnode) {
parent->lchild=fnode->lchild; if(t!=NULL) {
else printf("%5d",t->data);
parent->rchild=fnode->lchild; preorder(t->lchild);
free(fnode); preorder(t->rchild);
return; }
} }

Implementing Binary Search Tree ( continued )
void postorder(struct node *t) { printf("nEnter the key of node to be deleted : ");
if(t!=NULL) { scanf("%d",&key);
postorder(t->lchild); delnode(&root,key);
postorder(t->rchild); printf("nInorder traversal after deletion :n");
printf("%5d",t->data); inorder(root);
} }
}
int main() {
struct node *root=NULL; Output :
int n,i,num,key; Enter no of nodes in the tree : 5
printf("Enter no of nodes in the tree : "); Enter the element : 18
Enter the element : 13
scanf("%d",&n);
Enter the element : 8
for(i=0;i<n;i++) {
printf("Enter the element : "); Enter the element : 21
scanf("%d",&num); Enter the element : 20
insert(&root,num);
Preorder traversal :
}
18 13 8 21 20
printf("nPreorder traversal :n");
Inorder traversal :
preorder(root);
printf("nInorder traversal :n"); 8 13 18 20 21
inorder(root); Postorder traversal :
printf("nPostorder traversal :n"); 8 13 20 21 18
Enter the key of node to be searched : 13
postorder(root);
printf("nEnter the key of node to be searched : ");
scanf("%d",&key); Node exists
search(root,key); Enter the key of node to be deleted : 20
if(fnode==NULL)
Inorder traversal after deletion :
printf("nNode does not exist");
8 13 18 21
else printf("nNOde exists");

Arithmetic Expression Tree
Binary Tree associated with Arithmetic expression is called Arithmetic Expression Tree
 All the internal nodes are operators
 All the external nodes are operands
 When Arithmetic Expression tree is traversed in in-order, the output is In-fix expression.
 When Arithmetic Expression tree is traversed in post-order, We will obtain Post-fix expression.

Example: Expression Tree for (2 * (a − 1) + (3 * b))

+ In-Order Traversal of Expression Tree
Results In-fix Expression.

* * 2*(a–1)+(3*b)

Post-Order Traversal of Expression Tree
2 - 3 b Results Post-fix Expression.

2a1–* 3b* +
a 1

To convert In-fix Expression to Post-fix expression, First construct an expression
tree using infix expression and then do tree traversal in post order.

Graphs
A Tree is in fact a special type of graph. Graph is a data structure having a group of nodes
connecting with cyclic paths.
A Graph contains two finite sets, one is set of nodes is called vertices and other is set of edges.
A Graph is defined as G = ( V, E ) where.
i) V is set of elements called nodes or vertices.
ii) E is set of edges, identified with a unique pair ( v1, v2 ) of nodes. Here ( v1, v2 ) pair denotes that
there is an edge from node v1 to node v2.

Un-directed Graph Directed Graph A
A

C
B
B C

D E
D E
Set of vertices = { A, B, C, D, E }
Set of edges = { ( A, B ) , ( A, C ) , ( B, B ), ( B, D ),
Set of vertices = { A, B, C, D, E } ( C, A ), ( C, D ), ( C, E ) , ( E, D ) }
Set of edges = { ( A, B ) , ( A, C ) , ( B, D ), A graph in which every edge is directed is known as
( C, D ),( C, E ) , ( D, E ) } Directed graph.
A graph in which every edge is undirected is The set of edges are ordered pairs.
known as Un directed graph. Edge ( A, B ) and ( B, A ) are treated as different edges.
The set of edges are unordered pairs. The edge connected to same vertex ( B, B ) is called loop.
Edge ( A, B ) and ( B, A ) are treated as same Out degree : no of edges originating at a given node.
edge. In degree : no of edges terminating at a given node.
For node C - In degree is 1 and out degree is 3 and
total degree is 4.

Representation of Graph

A Set of vertices = { A, B, C, D, E }
Set of edges = { ( A, B ) , ( A, C ) , ( A, D ), ( B, D ), ( B, D ),
( C, D ),( C, E ) , ( D, E ) }
B C There are two ways of representing a graph in memory.
v) Sequential Representation by means of Adjacency Matrix.
vi) Linked Representation by means of Linked List.
D
E
Linked List

Adjacency Matrix
A B C D NULL

A B C D E
A 0 1 1 1 0 B A C D NULL
B 1 0 1 1 0
C 1 1 0 1 1 E NULL
C A B D
D 1 1 1 0 1
E 0 0 1 1 0
C E NULL
D A B
Adjacency Matrix is a bit matrix which
contains entries of only 0 and 1 D NULL
N E C
The connected edge between to vertices is
represented by 1 and absence of edge is
represented by 0.
Adjacency matrix of an undirected graph is
symmetric.

C Language Unit-8

More Related Content

Similar to C Language Unit-8 (20)

More from kasaragadda srinivasrao (8)

Recently uploaded (20)

C Language Unit-8