Digital and Logic Design Chapter 1 binary_systems
16 likes16,542 views
This document discusses binary number systems and digital computing. It covers binary numbers, number base conversions between decimal, binary, octal and hexadecimal. It also discusses binary coding techniques like binary-coded decimal, signed magnitude representation, one's complement and two's complement representations for negative numbers.
Digital and Logic Design Chapter 1 binary_systems
- 1. CHAPTER 1: BINARY SYSTEMS DIGITAL COMPUTER & DIGITAL SYSTEMS BINARY NUMBERS NUMBER BASE CONVERSION COMPLEMENTS SIGNED BINARY NUMBERS BINARY CODES BINARY STORAGE ELEMENTS 0 / 45
- 2. Digital Systems Discrete Data ● Examples: ♦ 26 letters of the alphabet (A, B … etc) ♦ 10 decimal digits (0, 1, 2 … etc) ● Combine together Analog Discrete ♦ Words are made of letters (University … etc) ♦ Numbers are made of digits (4241 … etc) Binary System ● Only ‘0’ and ‘1’ digits ● Can be easily implemented in electronic circuits 1 / 45
- 3. Decimal Number System Base (also called radix) = 10 ● 10 digits { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } Digit Position ● Integer & fraction Digit Weight ● Weight = (Base) Position Magnitude ● Sum of “Digit x Weight” Formal Notation 2 1 0 -1 -2 5 1 2 7 4 100 10 1 0.1 0.01 500 10 2 0.7 0.04 d2*B2+d1*B1+d0*B0+d-1*B-1+d-2*B-2 2 / 45 (512.74)10
- 4. Octal Number System Base = 8 ● 8 digits { 0, 1, 2, 3, 4, 5, 6, 7 } Weights ● Weight = (Base) Position Magnitude ● Sum of “Digit x Weight” Formal Notation 64 8 1 1/8 1/64 5 1 2 7 4 2 1 0 -1 -2 5 *82+1 *81+2 *80+7 *8-1+4 *8-2 3 / 45 =(330.9375)10 (512.74)8
- 5. Binary Number System Base = 2 ● 2 digits { 0, 1 }, called binary digits or “bits” Weights ● Weight = (Base) Position Magnitude ● Sum of “Bit x Weight” Formal Notation 1 *22+0 *21+1 *20+0 *2-1+1 *2-2 Groups of bits 4 bits = Nibble 8 bits = Byte 4 2 1 1/2 1/4 1 0 1 0 1 2 1 0 -1 -2 4 / 45 =(5.25)10 (101.01)2 1 0 1 1 1 1 0 0 0 1 0 1
- 6. Hexadecimal Number System Base = 16 ● 16 digits { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F } Weights ● Weight = (Base) Position Magnitude ● Sum of “Digit x Weight” Formal Notation 256 16 1 1/16 1/256 1 E 5 7 A 2 1 0 -1 -2 1 *162+14 *161+5 *160+7 *16-1+10 *16-2 5 / 45 =(485.4765625)10 (1E5.7A)16
- 7. The Power of 2 6 / 45 n 2n 0 20=1 1 21=2 2 22=4 3 23=8 4 24=16 5 25=32 6 26=64 7 27=128 n 2n 8 28=256 9 29=512 10 210=1024 11 211=2048 12 212=4096 20 220=1M 30 230=1G 40 240=1T Kilo Mega Giga Tera
- 8. Addition Decimal Addition 7 / 45 1 1 Carry 5 5 + 5 5 1 1 0 = Ten ≥ Base Subtract a Base
- 9. Binary Addition Column Addition 8 / 45 1 1 1 1 0 1 + 1 0 1 1 1 1 0 1 0 1 0 0 ≥ (2)10 1 1 1 1 1 1 = 61 = 23 = 84
- 10. Binary Subtraction Borrow a “Base” when needed 9 / 45 0 0 0 0 0 1 1 0 1 − 1 0 1 1 1 0 1 1 0 1 1 0 = (10)2 2 2 2 2 1 1 = 77 = 23 = 54
- 11. Binary Multiplication Bit by bit 10 / 45 1 0 1 1 1 1 0 1 0 0 0 0 0 0 1 0 1 1 1 0 0 0 0 0 x 1 0 1 1 1 1 1 1 0 0 1 1 0
- 12. Number Base Conversions 11 / 45 Decimal (Base 10) Octal (Base 8) Binary (Base 2) Hexadecimal (Base 16) Evaluate Magnitude Evaluate Magnitude Evaluate Magnitude
- 13. Decimal (Integer) to Binary Conversion Divide the number by the ‘Base’ (=2) Take the remainder (either 0 or 1) as a coefficient Take the quotient and repeat the division 12 / 45 Example: (13)10 Quotient Remainder Coefficient 13/ 2 = 6 1 a0 = 1 6 / 2 = 3 0 a1 = 0 3 / 2 = 1 1 a2 = 1 1 / 2 = 0 1 a3 = 1 Answer: (13)10 = (a3 a2 a1 a0)2 = (1101)2 MSB LSB
- 14. Decimal (Fraction) to Binary Conversion Multiply the number by the ‘Base’ (=2) Take the integer (either 0 or 1) as a coefficient Take the resultant fraction and repeat the division 13 / 45 Example: (0.625)10 Integer Fraction Coefficient a-1 = 1 0.625 * 2 = 1 . 25 0.25 * 2 = 0 . 5 a-2 = 0 0.5 * 2 = 1 . 0 a-3 = 1 Answer: (0.625)10 = (0.a-1 a-2 a-3)2 = (0.101)2 MSB LSB
- 15. Decimal to Octal Conversion 14 / 45 Example: (175)10 Quotient Remainder Coefficient 175 / 8 = 21 7 a0 = 7 21 / 8 = 2 5 a1 = 5 2 / 8 = 0 2 a2 = 2 Answer: (175)10 = (a2 a1 a0)8 = (257)8 Example: (0.3125)10 Integer Fraction Coefficient a-1 = 2 0.3125 * 8 = 2 . 5 0.5 * 8 = 4 . 0 a-2 = 4 Answer: (0.3125)10 = (0.a-1 a-2 a-3)8 = (0.24)8
- 16. Binary − Octal Conversion 8 = 23 Each group of 3 bits represents an octal digit Octal Binary 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 15 / 45 Example: Assume Zeros ( 1 0 1 1 0 . 0 1 )2 ( 2 6 . 2 )8 Works both ways (Binary to Octal & Octal to Binary)
- 17. Binary − Hexadecimal Conversion 16 = 24 Each group of 4 bits represents a hexadecimal digit Hex Binary 0 0 0 0 0 1 0 0 0 1 2 0 0 1 0 3 0 0 1 1 4 0 1 0 0 5 0 1 0 1 6 0 1 1 0 7 0 1 1 1 8 1 0 0 0 9 1 0 0 1 A 1 0 1 0 B 1 0 1 1 C 1 1 0 0 D 1 1 0 1 E 1 1 1 0 F 1 1 1 1 16 / 45 Example: Assume Zeros ( 1 0 1 1 0 . 0 1 )2 ( 1 6 . 4 )16 Works both ways (Binary to Hex & Hex to Binary)
- 18. Octal − Hexadecimal Conversion Convert to Binary as an intermediate step 17 / 45 Example: ( 2 6 . 2 )8 ( 0 1 0 1 1 0 . 0 1 0 )2 ( 1 6 . 4 )16 Assume Zeros Assume Zeros Works both ways (Octal to Hex & Hex to Octal)
- 19. Decimal, Binary, Octal and Hexadecimal 18 / 45 Decimal Binary Octal Hex 00 0000 00 0 01 0001 01 1 02 0010 02 2 03 0011 03 3 04 0100 04 4 05 0101 05 5 06 0110 06 6 07 0111 07 7 08 1000 10 8 09 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F
- 20. Complements 1’s Complement (Diminished Radix Complement) ● All ‘0’s become ‘1’s ● All ‘1’s become ‘0’s Example (10110000)2 (01001111)2 If you add a number and its 1’s complement … 19 / 45 1 0 1 1 0 0 0 0 + 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1
- 21. Complements 2’s Complement (Radix Complement) ● Take 1’s complement then add 1 ● Toggle all bits to the left of the first ‘1’ from the right Example: Number: 1’s Comp.: 20 / 45 1 0 1 1 0 0 0 0 0 1 0 0 1 1 1 1 + 1 0 1 0 1 0 0 0 0 OR 1 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0
- 22. Negative Numbers Computers Represent Information in ‘0’s and ‘1’s ● ‘+’ and ‘−’ signs have to be represented in ‘0’s and ‘1’s 3 Systems ● Signed Magnitude ● 1’s Complement ● 2’s Complement All three use the left-most bit to represent the sign: ♦ ‘0’ positive ♦ ‘1’ negative 21 / 45
- 23. Signed Magnitude Representation Magnitude is magnitude, does not change with sign S Magnitude (Binary) (+3)10 ( 0 0 1 1 )2 (−3)10 ( 1 0 1 1 )2 Sign Magnitude Can’t include the sign bit in ‘Addition’ 22 / 45 0 0 1 1 (+3)10 + 1 0 1 1 (−3)10 1 1 1 0 (−6)10
- 24. 1’s Complement Representation Positive numbers are represented in “Binary” Negative numbers are represented in “1’s Comp.” (+3)10 (0 011)2 (−3)10 (1 100)2 There are 2 representations for ‘0’ (+0)10 (0 000)2 (−0)10 (1 111)2 23 / 45 0 Magnitude (Binary) 1 Code (1’s Comp.)
- 25. 1’s Complement Range 4-Bit Representation 24 = 16 Combinations − 7 ≤ Number ≤ + 7 −23+1 ≤ Number ≤ +23 − 1 n-Bit Representation −2n−1+1 ≤ Number ≤ +2n−1 − 1 24 / 45 Decimal 1’s Comp. + 7 0 1 1 1 + 6 0 1 1 0 + 5 0 1 0 1 + 4 0 1 0 0 + 3 0 0 1 1 + 2 0 0 1 0 + 1 0 0 0 1 + 0 0 0 0 0 − 0 1 1 1 1 − 1 1 1 1 0 − 2 1 1 0 1 − 3 1 1 0 0 − 4 1 0 1 1 − 5 1 0 1 0 − 6 1 0 0 1 − 7 1 0 0 0
- 26. 2’s Complement Representation Positive numbers are represented in “Binary” Negative numbers are represented in “2’s Comp.” (+3)10 (0 011)2 (−3)10 (1 101)2 There is 1 representation for ‘0’ (+0)10 (0 000)2 (−0)10 (0 000)2 25 / 45 0 Magnitude (Binary) 1 Code (2’s Comp.) 1’s Comp. 1 1 1 1 + 1 1 0 0 0 0
- 27. 2’s Complement Range 4-Bit Representation 24 = 16 Combinations − 8 ≤ Number ≤ + 7 −23 ≤ Number ≤ + 23 − 1 n-Bit Representation −2n−1 ≤ Number ≤ + 2n−1 − 1 Decimal 2’s Comp. 26 / 45 + 7 0 1 1 1 + 6 0 1 1 0 + 5 0 1 0 1 + 4 0 1 0 0 + 3 0 0 1 1 + 2 0 0 1 0 + 1 0 0 0 1 + 0 0 0 0 0 − 1 1 1 1 1 − 2 1 1 1 0 − 3 1 1 0 1 − 4 1 1 0 0 − 5 1 0 1 1 − 6 1 0 1 0 − 7 1 0 0 1 − 8 1 0 0 0
- 28. Number Representations 4-Bit Example 27 / 45 Unsigned Binary Signed Magnitude 1’s Comp. 2’s Comp. Range 0 ≤ N ≤ 15 -7 ≤ N ≤ +7 -7 ≤ N ≤ +7 -8 ≤ N ≤ +7 Positive 0 0 0 Binary Binary Binary Binary Negative X 1 1 1 Binary 1’s Comp. 2’s Comp.
- 29. Binary Subtraction Using 1’s Comp. Addition Change “Subtraction” to “Addition” If “Carry” = 1 then add it to the LSB, and the result is positive (in Binary) If “Carry” = 0 then the result is negative (in 1’s Comp.) (5)10 – (6)10 (+5)10 + (-6)10 28 / 45 (5)10 – (1)10 (+5)10 + (-1)10 0 1 0 1 + 1 1 1 0 0 0 1 1 + 0 1 0 0 0 1 0 1 + 1 0 0 1 0 1 1 1 0 1 1 1 0 + 4 − 1 1
- 30. Binary Subtraction Using 2’s Comp. Addition Change “Subtraction” to “Addition” If “Carry” = 1 ignore it, and the result is positive (in Binary) If “Carry” = 0 then the result is negative (in 2’s Comp.) (5)10 – (6)10 (+5)10 + (-6)10 29 / 45 (5)10 – (1)10 (+5)10 + (-1)10 0 1 0 1 + 1 1 1 1 1 0 1 0 0 0 1 0 1 + 1 0 1 0 0 1 1 1 1 + 4 − 1
- 31. Binary Codes Group of n bits ● Up to 2n combinations ● Each combination represents an element of information Binary Coded Decimal (BCD) ● Each Decimal Digit is represented by 4 bits ● (0 – 9) Valid combinations ● (10 – 15) Invalid combinations 30 / 45 Decimal BCD 0 0 0 0 0 1 0 0 0 1 2 0 0 1 0 3 0 0 1 1 4 0 1 0 0 5 0 1 0 1 6 0 1 1 0 7 0 1 1 1 8 1 0 0 0 9 1 0 0 1
- 32. BCD Addition One decimal digit + one decimal digit ● If the result is 1 decimal digit ( ≤ 9 ), then it is a simple binary addition Example: ● If the result is two decimal digits ( ≥ 10 ), then binary addition gives invalid combinations Example: 31 / 45 5 + 3 8 0 1 0 1 + 0 0 1 1 1 0 0 0 5 + 5 1 0 0 1 0 1 + 0 1 0 1 0 0 0 1 0 0 0 0 1 0 1 0
- 33. BCD Addition If the binary result is greater than 9, correct the result by adding 6 32 / 45 5 + 5 1 0 0 1 0 1 + 0 1 0 1 1 0 1 0 + 0 1 1 0 0 0 0 1 0 0 0 0 Two Decimal Digits Multiple Decimal Digits 3 5 1 0 0 1 1 0 1 0 1 0 0 0 1
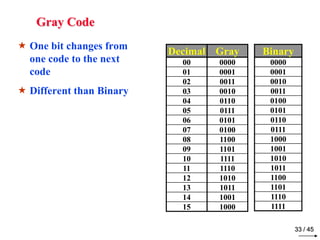
- 34. Gray Code One bit changes from one code to the next code Different than Binary Binary 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 33 / 45 Decimal Gray 00 0000 01 0001 02 0011 03 0010 04 0110 05 0111 06 0101 07 0100 08 1100 09 1101 10 1111 11 1110 12 1010 13 1011 14 1001 15 1000
- 35. ASCII Code American Standard Code for Information Interchange 34 / 45 Info 7-bit Code A 1000001 B 1000010 ... ... Z 1011010 a 1100001 b 1100010 ... ... z 1111010 @ 1000000 ? 0111111 + 0101011
- 36. Error Detecting Codes Parity One bit added to a group of bits to make the total number of ‘1’s (including the parity bit) even or odd ● Even ● Odd 1 0 1 1 1 0 1 0 0 0 0 0 1 0 0 1 1 1 1 1 0 0 0 0 0 1 Good for checking single-bit errors 35 / 45 4-bit Example 7-bit Example
- 37. Binary Logic Operators ● NOT If ‘x’ = 0 then NOT ‘x’ = 1 If ‘x’ = 1 then NOT ‘x’ = 0 ● AND If ‘x’ = 1 AND ‘y’ = 1 then ‘z’ = 1 Otherwise ‘z’ = 0 ● OR If ‘x’ = 1 OR ‘y’ = 1 then ‘z’ = 1 Otherwise ‘z’ = 0 36 / 45
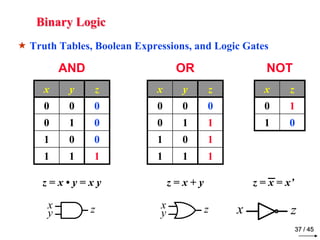
- 38. Binary Logic Truth Tables, Boolean Expressions, and Logic Gates z = x • y = x y z = x + y z = x = x’ xy AND OR NOT z 37 / 45 x y z 0 0 0 0 1 0 1 0 0 1 1 1 x y z 0 0 0 0 1 1 1 0 1 1 1 1 x z 0 1 1 0 xy z x z
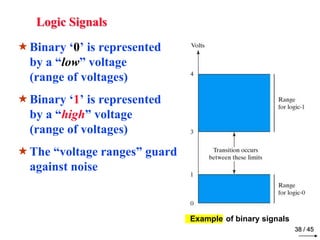
- 39. Logic Signals Binary ‘0’ is represented by a “low” voltage (range of voltages) Binary ‘1’ is represented by a “high” voltage (range of voltages) The “voltage ranges” guard against noise 38 / 45 Example of binary signals
- 40. Switching Circuits 39 / 45 AND OR
- 41. Homework Mano ● Chapter 1 Write your family name in ASCII with odd parity Decode the following ASCII ♦ 1-2 ♦ 1-7 string (with MSB = parity): ♦ 1-9 11000011 01101111 11101101 ♦ 1-10 11110000 11000000 01010000 ♦ 1-11 01010011 01010101 11010100 ♦ 1-16 Is the parity even or odd? ♦ 1-18 ♦ 1-20 ♦ 1-24(a) ♦ 1-29 40 / 45
- 42. Homework Mano 41 / 45 1-2 What is the exact number of bytes in a system that contains (a) 32K byte, (b) 64M byte, and (c) 6.4G byte? 1-7 Express the following numbers in decimal: (10110.0101)2, (16.5)16, and (26.24)8. 1-9 Convert the hexadecimal number 68BE to binary and then from binary convert it to octal. 1-10 Convert the decimal number 345 to binary in two ways: (a) convert directly to binary, (b) convert first to hexadecimal, then from hexadecimal to binary. Which method is faster?
- 43. Homework 42 / 45 1-11 Do the following conversion problems: (a) Convert decimal 34.4375 to binary. (b) Calculate the binary equivalent of 1/3 out to 8 places. Then convert from binary to decimal. How close is the result to 1/3? (c) Convert the binary result in (b) into hexadecimal. Then convert the result to decimal. Is the answer the same? 1-16 Obtain the 1’s and 2’s complements of the following binary numbers: (a) 11101010 (b) 01111110 (c) 00000001 (d) 10000000 (e) 00000000
- 44. Homework 43 / 45 1-18 Perform subtraction on the following unsigned binary numbers using the 2’s-complement of the subtrahend. Where the result should be negative, 2’s complement it and affix a minus sign. (a) 11011 – 11001 (b) 110100 – 10101 (c) 1011 – 110000 (d) 101010 – 101011 1-20 Convert decimal +61 and +27 to binary using the signed- 2’s complement representation and enough digits to accommodate the numbers. Then perform the binary equivalent of (+27) + (– 61), (–27) + (+61) and (–27) + (–61). Convert the answers back to decimal and verify that they are correct.
- 45. Homework 44 / 45 1-24 Represent decimal number 6027 in (a) BCD 1-29 The following is a string of ASCII characters whose bit patterns have been converted into hexadecimal for compactness: 4A EF 68 6E 20 C4 EF E5. Of the 8 bits in each pair digit, the leftmost is a parity bit. The remaining bits are the ASCII code. (a) Convert to bit form and decode the ASCII (b) Determine the parity used: odd or even.