Chapter 4.pptx compiler design lecture note

Chapter Four
Top-Down Parsing
Compiler Design
1

Objective
At the end of this session students will be able to:
 Understand the basics of Parsing techniques(Top-DownVs. Bottom-Up parsing).
 Understand the Recursive Descent Parsers: First and Fellow sets and how to find fisrt and
fellow sets of a parser, LL(1) parseTables.
 Understand about Grammars that are not LL(1): Removing Ambiguity, Removing left
recursion, left factoring
 Be familiar with LL(k) grammars.
 Understand the Javacc –A LL(k) Parser Generator.
 JavaCC file format Revised
 JavaCC Rules
 Anonymous tokens
 Using LOOKAHEAD Directives
 Ambiguity in JavaCC rules
 Writing a parser for simpleJava Using Javacc
2

Parsing and Parsers
 Once we have described the syntax of our programming language using a context-free
grammar, the next step is to determine if a string of tokens returned from the lexical
analyzer could be derived from that context-free grammar
 Determining if a sequence of tokens is syntactically correct is called parsing
 Two main strategies:
A. Top-down parsing: Start at the root of the parse tree and grow toward leaves
(modern parsers: e.g. JavaCC)
o Pick a production rule & try to match the input
o Bad “pick”  may need to backtrack
B. Bottom-up parsing: Start at the leaves and grow toward root (earlier parsers:
e.g. yacc)
o As input is consumed, encode possible parse trees in an internal state
o Bottom-up parsers handle a large class of grammars
3

Contd.
LL(1) parsers, recursive descent Parsers
Left-to-right input
Leftmost derivation
1 symbol of look-ahead
LR(1) parsers, operator precedence
Left-to-right input
Rightmost derivation
1 symbol of look-ahead
Also: LL(k), LR(k), SLR, LALR, …
4
Grammars that this can
handle are called LL(1)
grammars
Grammars that this can
handle are called LR(1)
grammars

Recursive Descent Parsers
 Top-down parsers are usually implemented as a mutual recursive suite of functions that
descend through a parse tree for the string, and as such are called “recursive descent
parsers” (RDP).
 Recursive descent parsers fall into a class of parsers known as LL(k) parsers
 LL(k) stands for Left-to-right, Leftmost-derivation, k-symbol lookahead parsers
 We first examine LL(1) parsers – LL parsers with one symbol lookahead
 To build the RDP, at first, we need to create the “First” and “Follow” sets of the non-terminals
in the CFG.
Example: A CFG and a CFG in its RDP form
Terminals = { id, num, while, print,>, {, }, ;, (, ) }
Non-Terminals = { S, E, B, L }
Rules = (1) S  print(E);
(2) S  while (B) S
(3) S  { L }
(4) E  id
(5) E  num
(6) B  E > E
(7) L  SL|ε
Start Symbol = S
5
Terminals = { e, f, g , h, i }
Non-Terminals = {S',S,A, B, C, D }
Rules = (0) S'  S$
(1) S  AB
(2) S  Cf
(3)A  ef
(4)A  ε
(5) B  hg
(6) C  DD
(7) C  fi
(8) D  g
Start Symbol = S'
b
)
C
F
G
i
n
i
t
s
R
D
P
f
o
r
m
a
)
C
F
G
n
o
t
i
n
i
t
s
R
D
P
f
o
r
m

First Sets and Follow Sets
Goal:- Given productions A → a |b , the parser should be able to choose
between a and b
How can the next input token help us decide?
Solution: FIRST sets
Informally: FIRST(a) is the set of tokens that could appear as the first symbol in a
string derived from a
Def:x in FIRST(a) iff a →* x g
First Sets
 The First set of a non-terminalA is the set of all terminals that can begin a
string derived from A
 If the empty string ε can be derived fromA, then ε is also in the First set ofA
6

Contd.
For instance, given the CFG below ($ is an end-of-file marker, ε means empty string ) :
Terminals = { e, f, g , h, i }
Non-Terminals = {S',S,A, B, C, D }
Rules = (0) S'  S$
(1) S  AB|Cf
(3)A  ef|ε
(5) B  hg
(6) C  DD|fi
(8) D  g
Start Symbol = S'
7
 In this grammar, the set of all strings derivable
from the non-terminal S’ are {efhg, fi, gg,
hg}
 Thus, the First(S’) = {e,f,g,h}, where e,f,g
and h are the first terminal of each string in
the above terminal set, respectively
 Similarly, we can derive the First sets of S, A,
B, C and D as follows:
First(S) = {e,f,g,h}
First(A) = {e, ε}
First(B) = {h}
First(C) = {f,g}
First(D) = {g}
First(DD) = {g}
First(AB) = {e, h}
First(efB) = {e}
First(AC) = {e, f, g}
First(AA) = {e, ε}

Contd.
Follow Sets
 For each non-terminal in a grammar, we can also create a Follow set.
 The Follow set for a non-terminal A in a grammar is the set of all terminals that
could appear right afterA in a valid sentence while driving it.
 Take another look at the CFG shown in slide no. 5 above, what terminals can followA
in a derivation?
o Consider the derivation S’  S$  AB$  Ahg$, since h follows A in this
derivation, h is in the Follow set ofA. Note: $ is the end-of-file marker.
o What about the non-terminal D? Consider the partial derivation: S’  S$ 
Cf$  DDf$  Dgf$.
o Since both f and g follow a D in this derivation, f and g are in the Follow set of
8

Contd.
 The follow sets for all non-terminals in the CFG are shown below:
9
Fellow(S') = { }
Fellow(S) = {$}
Fellow(A) = {h}
Fellow(B) = {$}
Fellow (C) = {f}
Fellow (D) = {f, g}
= (0) S'  S$
(1) S  AB|Cf
(3)A  ef|ε
(5) B  hg
(6) C  DD|fi
(8) D  g

Finding First and Follow Sets
 To calculate the First set of a non-terminal A, we need to calculate the First set of a
string of terminals and non-terminals, since the rules that define what a non-terminal
can derive contain terminals and non-terminals.
 The First set of a string of terminals and non-terminals  can be defined recursively
using the following two algorithms:
Algorithm to calculate First( ), for a string ofTerminals and Non-Terminals
 If = ε then First()= ε
 If the first symbol in  is the terminal a, then First()={a}
 If = A' for some non-terminal A, and (possibly empty) string of terminals and
non-terminals ':
o If First(A) does not contain ε, then First()=First(A)
o If First(A) does contain ε, then First()=(First(A)-{ε})  First(')
10

Contd.
Algorithm to calculate First sets for all Non-Terminals in CFG G
1. For each non-terminal A in G, set First(A)= { }
2. For each rule A
 (where  is a string of terminals and non-terminals), add all
elements of First() to First(A). That is:
o If = ε add ε to First(A)
o If the first character in  is the terminal a, then add a to First(A)
o If = A1' for some non-terminal A1, and First(A1) does not contain ε,
then add all elements of First(A1) to First(A)
o If = A1' for some non-terminal A1, and First(A1) does contain ε, then
add all elements of First(A1) (other than ε) to First(A), and recursively add
all elements of First(') to First(A)
3. If any changes were made in step 2, go back and to 2 and repeat
11

Example
Consider the CFG given on slide no. 7 above is G.
o Initially, for each non-terminalA in G we set First(A) = { }, an empty set
o We then go through one iteration of the algorithm, which will modify the first set
as follows:
(0) S'  S$.Add { } to First(S' ) ={ } (no change)
(1) S  AB.Add { } to First(S) = { } (no change)
(2) S  C.Add { } to First(S) = { } (no change)
(3)A  ef.Add e to First(A) = {e}
(4)A  ε. Add ε to First(A) = {e, ε}
(5) B  hg.Add h to First(B) = {h}
(6) C  DD.Add { } to First(C) = { } (no change)
(7) C  fi.Add f to First(C) = {f}
(8) D  g.Add g to First(D) = {g}
Note: Since there were 5 changes, we need another iteration
12
Non-Terminals First Set
S' {}
S {}
A {e, ε}
B {h}
C {f}
D {g}

Contd.
(0) S'  S$.Add { } to First(S’) = { } (no change)
(1) S  AB.Add e,h to First(S) = {e, h}
(2) S  C.Add f to First(S) = {e, h, f}
(3)A  ef.Add e to First(A) = {e, ε} (no change)
(4)A  ε. Add ε to First(A) = {e, ε} (no change)
(5) B  hg.Add h to First(B) ={h} (no change)
(6) C  DD.Add g to First(C) = {f, g}
(7) C  fi.Add f to First(C) = {f, g} (no change)
(8) D  g.Add g to First(D) ={g} (no change)
13
S' {}
S {e, f, h}
A {e, ε}
B {h}
C {f, g}
D {g}

Contd.
(0) S’  S$.Add e,f,h to First(S’) = {e, f, h}
(1) S  AB.Add e,h to First(S) = {e, f, h} (no change)
(2) S  C.Add f,g to First(S) = {e, h, f, g}
(5) B  hg.Add h to First(B) = {h} (no change)
(6) C  DD.Add g to First(C) = {f, g} (no change)
(8) D  g.Add g to First(D) = {g} (no change)
14
S' {e, f, h}
S {e, f, g, h}
A {e, ε}
B {h}
C {f, g}
D {g}

Contd.
(0) S'  S$.Add e, f, g, h to First(S’) = {e, h, f, g}
(1) S  AB.Add e, h to First(S) = {e, f, h} (no change)
(2) S  C.Add f, g to First(S) = {e, h, f, g} (no change)
(5) B  hg.Add h to First(B) = {h} (no change)
(6) C  DD.Add g to First(C) = {f, g} (no change)
(8) D  g.Add g to First(D) = {g} (no change)
Note: Since there was 1 change, we need another iteration
15
S' {e, f, g, h}
S {e, f, g, h}
A {e, ε}
B {h}
C {f, g}
D {g}

Contd.
(0) S’  S$.Add e, f, g, h to First(S’) (no change)
(1) S  AB.Add e, f, h to First(S) (no change)
(2) S  C.Add f, g to First(S) (no change)
(3)A  ef.Add e to First(A) (no change)
(4)A  ε. Add ε to First(A) (no change)
(5) B  hg.Add h to First(B) (no change)
(6) C  DD.Add g to First(C) (no change)
(7) C  fi.Add f to First(C) (no change)
(8) D  g.Add g to First(D) (no change)
16
S' {e, f, g, h}
S {e, f, g, h}
A {e, ε}
B {h}
C {f, g}
D {g}
Since there were no changes, we stop
Note that within each iteration we can examine the rules in any order.
 If we examine the rules in a different order in each iteration, we will still achieve the same
result, but may take a different number of iterations.
 Check that an order of iteration 8,7,6,5,4,3,2,1,0 requires fewer number of iteration?

Finding Follow Sets for Non-Terminals
 If the grammar contains the rule: S  Aa, then a is in the Follow set of A, since a
appears immediately after A.
 If the grammar contains the rules:
S AB
B  a b
│
then both a and b are in the Follow set ofA,Why?
Consider the following two partial derivations:
S  AB  Aa
S  AB  Ab
So both a and b are in the Follow set ofA.
If the grammar contains the rules:
S  ABC
B  a b
│ │ ε
C  c d
│
then a, b, c and d are all in the Follow set ofA.Why?
17
S  ABC AaC
S  ABC AbC
S  ABC AC Ac
S  ABC AD Ad

Contd.
Consider the grammar:
S  Ax
A  C
then x is in the Follow sets ofA and C.Why?
Consider another grammar:
S  Ax
A  CD
D  ε
then x is in the Follow sets ofA, C and D.Why?
 The above examples lead us to the following method for finding the follow sets for
the non-terminals in a CFG
18
S  Ax Cx
S  Ax CDx CDx

Finding First and Follow Sets
 We can calculate the Follow sets from the First sets by using the recursive algorithm
given below:
Algorithm to calculate Fellow sets for all Non-Terminals in CFG G
1. Calculate First(A) for all non-terminals A in G
2. Set Fellow(A)={ } for all non-terminals A in G
3. For each rule A in G(where A is a non-terminal and  is a string of terminals
and non-terminals). For each non-terminal A1 in 
i. If the rule is of the form AA1, where  and  are (possibly empty)
strings of terminals and non-terminals, and First() does not contain ε, then
add all elements of First() to Fellow(A1)
ii. If the rule is of the form AA1, where  and  are (possibly empty)
strings of terminals and non-terminals, and First() does contain ε, then add
all elements of First() except ε to Fellow(A1) and add all elements of
Fellow(A) to Fellow(A1)
19

Example
Consider the following CFG, for which we calculate the First sets for all non-terminals:
Terminals = { a, b, c , d}
Non-Terminals = {{S,T, U,V}
Rules = (0) S'  S$
(1) S  TU
(2)T  aVa
(3)T  ε
(4) U  bVT
(5)V  Ub
(6)V  d
Start Symbol = S'
20
S' {a, b}
S {a, b}
T {a, ε}
U {b}
V {b, d}
The First sets of non-terminals are:
S' = {a,b}; S = {a,b};T = {a, ε}; U = {b};
andV = {b,d}

Contd.
Initially, for each non-terminal A in G we set Fellow(A) = { }, an empty set
(0) S'  S$ Add {$} to Follow (S) = {$}.
(1) S  TU Add First(U), {b}, to Follow(T) = {b}
Add Follow(S), {$}, to Follow(U) = {$}
(2)T  aVa Add {a} to Follow(V) = {a}
(3)T  ε (no change)
(4) U  bVT Add First(T), {a}, to Follow(V) = {a}
Add Follow(U), {$}, to Follow(T) = {b, $}
Add Follow(U), {$}, to Follow(V) = {a, $} (forT  ε)
(5)V  Ub Add {b} to Follow(U) = {b, $}
(6)V  d (no change)
The Follow sets of non-terminals are:
S’ = { }; S = {$};T = {b, $}; U = {b, $}; andV = {a,$}
Note: Since there were some changes, we need another iteration
21
Non-Terminals Fellow Set
S' {}
S {$}
T {b, $}
U {b, $}
V {a, $}

Contd.
(0) S’  S$ Add $ to Follow (S) = {$}. (no change)
(1) S  TU Add First(U), b, to Follow(T) = {b, $} (no change)
Add Follow(S), {$}, to Follow(U) = {b, $} (no change)
(2)T  aVa Add {a} to Follow(V) = {a, $} (no change)
(3)T  ε(no change)
(4) U  bVT Add First(T), a, to Follow(V) = {a, $} (no change)
Add Follow(U), {$}, to Follow(T) = {b, $} (no change)
Add Follow(U), {b, $}, to Follow(V) = {a, b, $} (forT  ε)
(5)V  Ub Add b to Follow(U) = {b, $} (no change)
S’ = { }; S = {$};T = {b, $}; U = {b, $}; andV = {a, b, $}
Note: Since there was 1 change, we need another iteration
22
S' {}
S {$}
T {b, $}
U {b, $}
V {a, b, $}

Contd.
(0) S’  S$ Add $ to Follow S = {$}.. (no change)
(1)S  TU Add First(U), b, to Follow(T ) = {b, $} (no change)
Add Follow(S), {$}, to Follow(U) = {b, $} (no change)
(2)T  aVa Add a to Follow(V) = {a, $} (no change)
(3)T  ε (no change)
(4) U  bVT Add First(T), a, to Follow(V) = {a, $} (no change)
Add Follow(U), {$}, to Follow(T) = {b, $} (no change)
Add Follow(U), {b, $}, to Follow(V) = {a, b, $} (no change)
(5)V  Ub Add b to Follow(U) = {b, $} (no change)
S’ = { }; S = {$};T = {b, $}; U = {b, $}; andV = {a, b, $}
Note: Since there were no changes, we stop.
23
S' {}
S {$}
T {b, $}
U {b, $}
V {a, b, $}

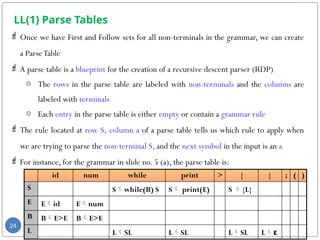
LL(1) Parse Tables
 Once we have First and Follow sets for all non-terminals in the grammar, we can create
a ParseTable
 A parse table is a blueprint for the creation of a recursive descent parser (RDP)
o The rows in the parse table are labeled with non-terminals and the columns are
labeled with terminals
o Each entry in the parse table is either empty or contain a grammar rule
 The rule located at row S, column a of a parse table tells us which rule to apply when
we are trying to parse the non-terminal S, and the next symbol in the input is an a
 For instance, for the grammar in slide no. 5 (a), the parse table is:
24
id num while print > { } ; ( )
S Swhile(B) S S print(E) S {L}
E Eid Enum
B BE>E BE>E
L LSL LSL LSL Lε

Contd.
 Once we have the parse table for a CFG, creating a recursive descent parser is easy.
o We need to write a function for each non-terminal S in the grammar.
o The row labeled S in the parse table will tell us exactly what the function parse S
needs to do.
Creating ParseTables
A parse table is created as follows:
1. The rows of the parse table are labeled with the non-terminals of the grammar.
2. The columns of the parse table are labeled with the terminals of the grammar
3. Each entry of the parse table is either empty or contains grammar rule.
o Place each rule of the form S  γ in row S in each column in First(γ), where γ is
the First set of terminals and non-terminals.
o Place each rule of the form S  γ in row S in each column in Follow(S), where
First(γ) contains ε.
25

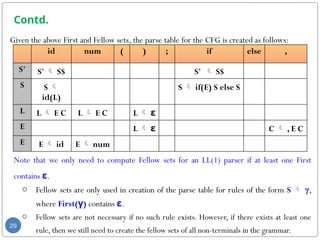
Example
Consider again the CFG in slide no 7 (b).We have the First and Follow sets of each non-
terminal:
The Resulting parse table is shown on next slide.
26
Non-
terminal
First Follow
S' {e,f,g,h
}
{ }
S {e,f,g,h
}
{$}
A {e,ε} {h}
B {h} {$}
C {f,g} {f}
D {g} {f,g}
(0) S'  S$ First(S')={e,f,g,h}. S'  S$ goes in row S',
columns e, f, g, h
(1) S  AB First(AB)={e, h}. S AB goes in row S, columns e, h
(2) S  C First(C)={f, g}. S C goes in row C, columns f, g
(3)A  ef First(ef)={e}. A ef goes in row A, column e
(4)A ε First(ε)={ε}
First(A)={h} A ε goes in row A, column h
(5) B  hg First(hg)={h}. B hg goes in row B, column h
(6) C  DD First(DD)={g}. C DD goes in row C, column g
(7) C  fi First(C)={f}. C fi goes in row C, column f
(8) D  g First(D)={g}. D g goes in row D, column g

Contd.
27
e f g h i
S' S'  S$ S'  S$ S'  S$ S'  S$
S S  AB S  C S  C S  AB
A A  ef A  ε
B B  hg
C C  fi C  DD
D D  g

Example 2
Given the following CFG create the LL(1) of the CFG :
Terminals = { id, num, (, ), ;, if, else, ,, $}
Non-Terminals = {S, S, L, C, E}
Rules = (0) S'  S$
(1) S  id(L);
(2) S  if(E) S else S
(3) L  ε
(4) L  E C
(5) C  ε
(6) C  , E C
(7) E  id
(6) E  num
Start Symbol = S'
28
Non-terminal First Follow
S' {id, if} { }
S {id, if} {$,else}
L {id, num, ε} { ) }
C {,, ε} { ) }
E {id, num} { ), ,}
Find the First and Fellow sets of each non-
terminal?

Contd.
Given the above First and Fellow sets, the parse table for the CFG is created as follows:
29
id num ( ) ; if else ,
S' S'  S$ S'  S$
S S 
id(L)
S  if(E) S else S
L L  E C L  E C L  ε
E L  ε C  , E C
E E  id E  num
Note that we only need to compute Fellow sets for an LL(1) parser if at least one First
contains ε.
o Fellow sets are only used in creation of the parse table for rules of the form S  γ,
where First(γ) contains ε.
o Fellow sets are not necessary if no such rule exists. However, if there exists at least one
rule, then we still need to create the fellow sets of all non-terminals in the grammar.

Contd.
Once we have the parse table, creating a suite of recursive functions is trivial.
For instance, the function to parse an S based on the above parse table is shown below:
void ParseS(){
switch(currentToken.kind){
case Constants.ID;
checkToken(Constants.ID);
checkToken(Constants.LEFT_PARENTHESIS);
ParseL();
checkToken(Constants.RIGHT_PARENTHESIS);
checkToken(Constants.SEMICOLON);
break;
case Constants.IF;
checkToken(Constants.IF);
checkToken(Constants.LEFT_PARENTHESIS);
ParseE(){;
checkToken(Constants.RIGHT_PARENTHESIS);
ParseS():
checkToken(Constants.ELSE);
ParseS():
break;
default:
error("Parse Error");
}}
30

Grammars That Are Not LL(1)
 If we can build an LL(1) parse table for a grammar that has no duplicate entries, then
we say that grammar is LL(1).
o Unfortunately, not all grammars are LL(1). For instance, the following grammar is
not LL(1) grammar.
Terminals = { id, +, - , *, /, % }
Non-Terminals = {E}
Rules = (0) E  id
(1) E  E + E|E - E
(3) E  E * E|E / E |E % E
Start Symbol = E
 The parse table includes only one non-terminal E, but it has 6 entries in the id column.
o Hence, the above grammar is ambiguous and we can not create an LL(1) parser for it.
o If we wish to be able to parse the grammar, we need to create an equivalent
grammar that is not ambiguous
31
+ - * / % id
E
E  id
E  E + E
E  E - E
E  E * E
E  E / E
E  E % E
ParseTable for the Grammar

Removing Ambiguity
There are four ways in which ambiguity can creep into (get into) a CFG for a
programming language:
1. Defining expressions:- the straightforward definition of expressions will often
lead to ambiguity, such as the one that we have seen in slide # 31 above.
2. Defining complex variables:- complex variables, such as instance variables in
classes, fields in records or structures, array subscripts and pointer references, can also
lead to ambiguity. Example V  id|V.V
3. Overlap between specific and general cases: For example CFG ,
Terminals = { id, +, - , *, /, % }
Non-Terminals = {E,T, F}
Rules =(0) E  E+T|E-T|T|id
(1)T T*F|T/F|T%F|F|id
(3) F (E)|id
Start Symbol = E
32
The terminal id has several leftmost
derivations (and hence several parse trees):
E  T , E  T  id, E  T  F  id

Contd.
4. Nesting statements:- the most common instance of nesting statements causing
ambiguity is the infamous "dangling else", whose CFG is shown below:
S  if e then S else S |S  if e then S
S  a|b
The above CFG has two parse trees
 It is not always possible to remove ambiguity from a context-free grammar.
o There are some languages that are inherently ambiguous. That is, there exists a
language L, such that all CFGs that generate L are ambiguous.
 Inherent ambiguity is not a problem that compiler designers usually need to
face. i.e. no major programming language is inherently ambiguous.
o There is no algorithm that will always remove ambiguity from a context-free
grammar
33
Draw the
Parse tree for
the CFG?

Removing Left Recursion
 An unambiguous grammar may still not be LL(1). Consider the unambiguous
expression grammar below:
Terminals = { id, +, - , *, /, % }
Non-Terminals = {E,T, F}
Rules =(1) E  E+T
(2) E  E -T
(3) E  T
(4)T  T*FT T/F
(5)T  T/F
(6)T  F
(7) F  (E)
(8) F  id
Start Symbol = E
34
 Though this CFG is unambiguous, it is not
LL(1). In order for a CFG to be LL(1), it must
be possible to decide which rule to apply after
looking at only the leftmost symbol of a
string.
 On seeing that rules an id, we cannot tell if we
should apply rule (1), (2), or (3).
 The problem with this CFG is (1), (2) are left-
recursive.
 A rule S  α (where S is a non-terminal and α
is a string of terminals and non-terminals) is
No left-recursive grammar
is LL(1)

Contd.
Consider the following CFG fragment:
(1) S  Sα
(2) S  β
What strings can be derived from S? Consider the following partial derivations:
S  S α  S α α  S α α α  β α α α
Any string that can be derived from S will be a string that can be derived from α followed
by zero or more strings that can be derived from β. Using EBNF notation, we have:
S  β(α)*
Using CFG notations, we have:
S  βA
A  αA
A  ε
35
We have removed the left-recursion in
the above example!!

Contd.
In general, the set of rules of the form:
S  Sα1; S  Sα2 ; S  Sα3 ; ..... ; S  Sαn
S  β1 ; S  β2 ; S  β3 ; ….. ; S  βn
Can be rewritten as:
S  BA
B  β1│β2│β3 …..
│ │βn
A  α1A│α2A│α3A .....
│ │αnA
A  ε
36
Let’s take a closer look at the expression
grammar:
E  E +T
E  E –T
E  T
Using the above transformation, we get
the following CFG, which has no left-
recursion:
E  TE'
E'  +TE'
E'  -TE'
E'  ε
Using EBNG notations, we have:
E  T((+E) (-E))*
│

Left Factoring
 Even if a CFG is unambiguous and has no left-recursion, it still may not be LL(1).
 Consider the following two Fortran do statements:
Fortran:
do
var = initial, final
loop body
end do
and
Fortran:
do
var = initial, final, inc
loop body
end do
37
Java/C equivalent:
for(var=initial; var<=final;var++)
{
loop body
}
and
Java/C equivalent:
for(var=initial; var<=final;var+=inc)
{
loop body
}

Contd.
We can describe the Fortran do statement with the following CFG fragment:
S  do LS
L  id = exp, exp
L  id = exp, exp, exp
This CFG is not LL(1).Why? Because there are two rules for L.We can not tell which rule
to use by looking only at the first symbol L.
We can fix this problem by left-factoring the similar section of the rule as follows:
S  do LS
L  id = exp, exp L'
L'  , exp
L'  ε
Using EBNF notations, the Fortran do statement can also be written as follows:
S  do LS
L  id = exp, exp (, exp)?
38

Contd.
 In general, if we have the following context-free grammar, where α and βk stand for
strings of terminals and non-terminals:
S  αβ1 ; S  αβ2 ; S  αβ3 ; ... ; S  αβn
We could left-factor it to get the CFG:
S  αB; B  β1 ; B  β2 ; B  β3 ; … ; B  βn
Using EBNF notations to get:
S  α(β1│β2│β3 …
│ │βn)
39

LL(K) Parsers
 LL(1) parser needs to decide which rule to apply after looking at only one token
 If more than one single token is required to determine which rule to apply, then the
grammar is not LL(1)
For instance, consider the following simple CFG:
Terminals = {a, b, c}
Non-terminals = {S}
Rules = (1) S  abc
(2) S  acb
Start symbol = S
 This grammar is not LL(1), since the LL(1) parse table has duplicate entries:
40
a b c
S S abc; S  acb

Contd.
 When trying to parse a string derivation from an S, we cannot tell which rule to
apply by looking at a single symbol; since all strings derivable from S start
with a.
 We could left-factor the grammar to make it LL(1)
 We also could modify our parser so that it examines the first two elements in
the string to determine which rule to apply
 The resulting parse table would be much larger as follows:
41
aa ab ac ba bb bc ca cb cc
S S abc S  acb

Contd.
 An LL(k) parser examines the first k symbols in the input before determining which
rule to apply
 In order to create an LL(k) parser, we need to generalize the definitions of First and
Follow sets
 Our definitions of generalized First and Follow sets will use the concept of k-
prefix
Definition1 k-prefix:The k-prefix of a string of terminals w is a string consisting
of the first k terminals in w. If w ≤ k, then the k-prefix of w is w
│ │ .
 The k-prefix of a set of strings is the set of K-prefixes of all strings in the set.
For example; given the terminals {a, b, c, d}, the 3-prefix of the set {abcd, abcc, abdd,
ab, ε} is the set {abc, abd, ab, ε}
42

Contd.
Definition 2 Firstk: The Firstk set of a non-terminal S is the k-prefix of the set of all
strings of terminals derivable from S.
The Firstk set of a string of terminals and non-terminal γ is the k-prefix of all strings of
terminals derivable from γ.
Definition 3 Followk: The Followk set of a non-terminal S is the k-prefix of the set of
all strings of terminals that follow S in a partial derivation.
43

Algorithm to calculate Firstk for non-terminals
1. For each non-terminal S in G, set Firstk(S) = { }
2. For each rule S  γ in G, add all elements of k-prefix(Firstk(γ)) to Firstk(S)
3. If any changes were made in step 2, go back to step 2 and repeat
44
Algorithm to calculate Firstk for a string of terminals and non-
terminals:
1. For any terminal a, Firstk(a) = {a}
2. For any string of terminals and non-terminals γ = γ1γ2γ3…γn, Firstk(γ) = k-
prefix( Firstk(γ1) First
○ k(γ2) First
○ k(γ3) … First
○ k(γn))

Algorithm to calculate Followk for non-terminals
1. Calculate Firstk(S) for all non-terminals S in G
2. Set Followk = { } for all non-terminals S in G
3. For each rule S  γ in G
For each non-terminal S1 in γ where γ = α S1β, add
[k-prefix(Firstk(β) ○ Followk(S))] to Followk(S1). If Followk(S) = { }, add [k-
prefix(Firstk(β))] to Followk(S1).
4. If any changes were made in step 3, go back to step 3 and repeat
45
Algorithm to create an LL(k) parse table
For each rule of the form S  γ, place the rule in row S, in all columns labeled with Firstk(γ)
Follow
○ k(S)

Local Lookahead in LL(k) Parsers
 If a CFG has t terminals and n non-terminals, then the number of entries in the
LL(k) parse table can be n x tk
.This makes for some pretty big parse tables
 Rather than trying to create an LL(k) parser by creating a complete LL(k) parse
table, we can crate an LL(1) parse table, which may have duplicate entries
 When creating the parser from this parse table, we will use a local lookahead
greater than 1 to disambiguate multiple parse table entries
 For instance, consider the following CFG fragment for simple Java. Where S
generates statements and E generates expressions (Note: GETS means “=“)
S  <IDENTIFIER> <GETS> E <SEMICOLON>
S  <IDENTIFIER> <IDENTIFIER> <SEMICOLON>
 The parse table for this grammar will have a duplicate entry in row S, column
<IDENTIFIER>
 We can leave this duplicate entry in the parse table, and we can add an extra check
when we build the parser
46

Contd.
 See the ParserS() program given below:
ParseS(){
switch(currentToken.kind){
….
case simpleConstants.IDENTIFIER:
currentToken=simpleTokenMnager.getNextToken();
if(currentToken== simpleConstants.IDENTIFIER){
checkToken(simpleConstants.IDENTIFIER);
checkToken(simpleConstants.SEMICOLON);
}
else if(simpleConstants.GETS){
ParseS():
checkToken(simpleConstants.SEMICOLON);
}else{error(“Parse Error”);
…
}}
 JavaCC allows for both local (for the rules of one non-terminal) and global (for the
rules of all non-terminals) lookahead greater than 1.
47

JavaCC – A LL(k) Parser Generator
 JavaCC can be used to build lexical analyzers as well as recursive descent parsers
 JavaCC takes the EBNF grammar for a language as input, and creates a suite of mutually
recursive methods that implement a LL(k) parser for that language
JavaCC File Format Revisited
options {
/* Code to set various option flags */
}
PARSER_BEGIN(simple)
public class simple {
/* Extra parser method definitions go here,
/* often a main program which derives the parser. */
}
PARSER_END(simple)
TOKEN_MGR_DECLS:
{
/* Declarations used by the lexical analyzer */
}
/*Token rules and actions */
/* JavaCC rules and actions */
48

JavaCC Rules
JavaCC uses EBNF rules to describe the grammar of that language to be parsed
Each JavaCC rule has the form:
void nonTerminalName();
{ /* Java Declarations */}
{ /* Rule Declarations */}
 The “Java Declarations” block will be used for building abstract syntax trees, we will
leave this block blank for now
 The “Rule Declarations” block defines the right-hand side of the rules that we are
writing
 Non-terminals in these rules will represent function calls, and that will be followed
by ().Terminal names will be enclosed in < and >.
49

Contd.
For instance:
S while (E) S
S  V = E;
Would be represented by the JavaCC rule:
void statement ();
{ } /* the Java Declarations block is blank */
{
<WHILE> <LPAREN> expresssion() <RPAREN> statement()
│ variable() <GETS> expression() <SEMICOLON>
}
Note: JavaCC uses the uppercase letters for terminals and lowercase letters for non-
terminals
o All terminals are inside < and >
o Non-terminals represent method calls in the generated parser. Hence, the () after
each non-terminal in the rule
50

Using LOOKAHEAD Directives
 By default, JavaCC creates a LL(1) parser for the grammar described in the .jj file.
What if the grammar is not LL(1)?
Consider the following JavaCC rule:
void S():
{ }
{ “a”“b”“c”
”
│ a”“d”“c”
}
 The above rule can not appear in an LL(1) grammar, but it can appear in an LL(2)
grammar
o JavaCC not only generates LL(1) parsers, but also generates LL(k) parsers
 We can set the global LOOKAHEAD to 2 instead of 1 by adding the line
“LOOKAHEAD = 2; “ to the options section of the .jj file.
o But this will make the generated parser much larger
51

Contd.
 JavaCC allows us to change the value of the lookahead locally, instead of globally
 This could keep the flexibility and efficiency of using a lookahead of 1 for most of the
parser
 We can use the directive LOOKAHEAD(k) to lookahead k symbols locally. For
example:
void S():
{ }
{LOOKAHEAD(2)“a”“b”“c”
”
│ a”“d”“c”
}
Another example:
void():
{ }
{
“A” (LOOKAHEAD(2)(“B”“C”) (“B”“D”))
│
}
52
But the following example doesn’t work.Why?
void S():
{ }
{
LOOKAHEAD (2) “A” ((“B”“C”)
(“B”“D”))
│
}

Contd.
 Use LOOKAHEAD directive to solve the ambiguity of “if then else” statements
void statement():
{ }
{
<IF> expression() <THEN> statement() (LOOKAHEAD(1) <ELSE>
statement())?
│ /* other statement definitions */
}
53

Chapter 4.pptx compiler design lecture note

More Related Content

Similar to Chapter 4.pptx compiler design lecture note (20)

More from adugnanegero (9)

Recently uploaded (20)

Chapter 4.pptx compiler design lecture note