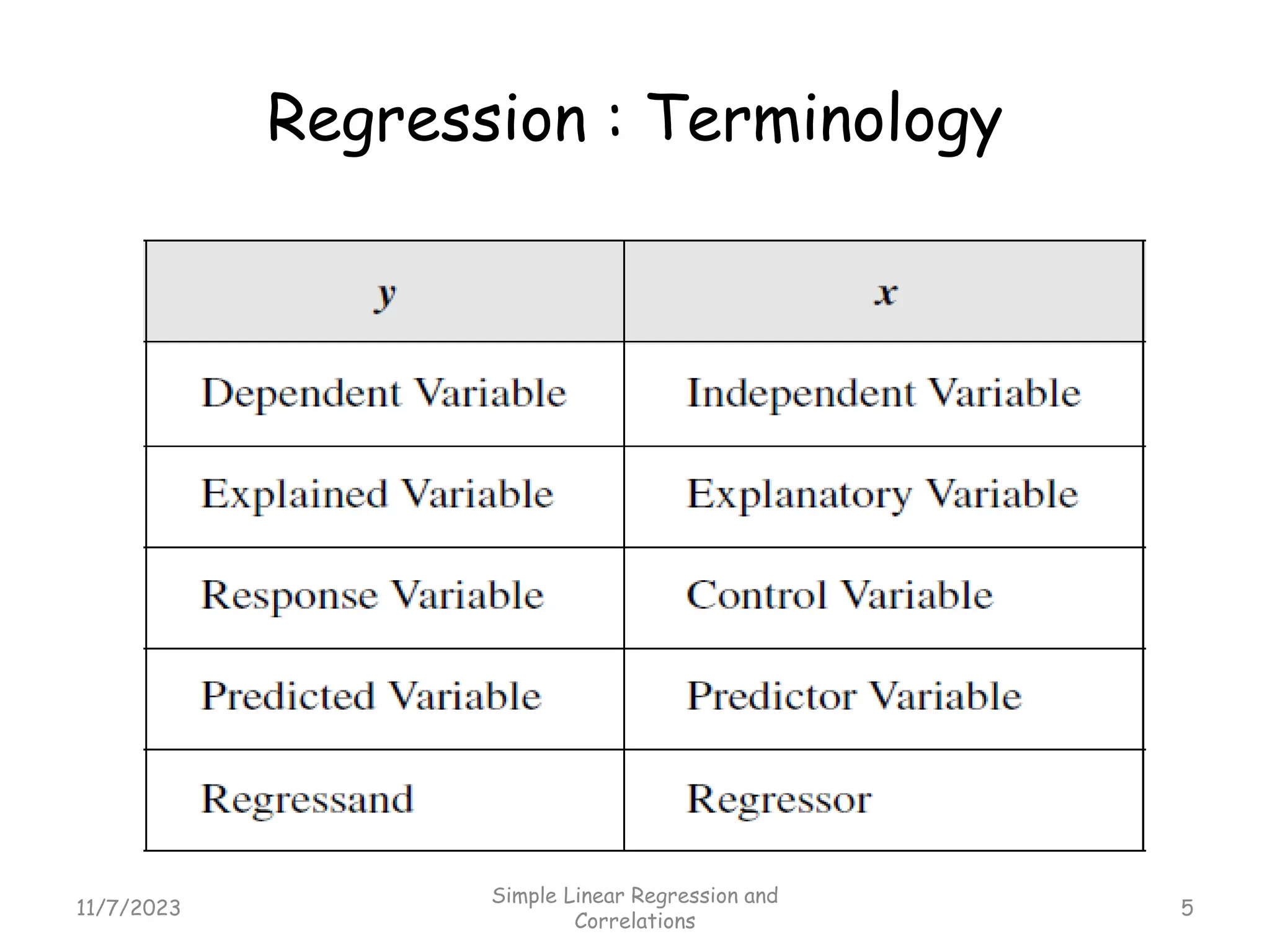
The document discusses simple linear regression and correlation. Simple linear regression predicts a dependent variable based on an independent variable. The linear regression equation is represented as y = β0 + β1x + ε, where β0 is the y-intercept, β1 is the slope, and ε is the error term. Multiple linear regression extends this to use two or more independent variables. Correlation is measured on a scale of -1 to 1 and indicates the strength and direction of the linear relationship between two variables. The coefficient of correlation r is calculated to quantify the correlation between variables.