![Measure of Impurity: GINI
Gini Index for a given node t :
(NOTE: p( j | t) is the relative frequency of class j at node t).
Maximum (1 - 1/nc) when records are equally distributed
among all classes, implying least interesting information
Minimum (0.0) when all records belong to one class,
implying most interesting information
∑−=
j
tjptGINI 2
)]|([1)(
C1 0
C2 6
Gini= 0.000
C1 2
C2 4
Gini= 0.444
C1 3
C2 3
Gini= 0.500
C1 1
C2 5
Gini= 0.278](https://image.slidesharecdn.com/160301117-171130014410/85/Classification-Basic-Concepts-and-Decision-Trees-35-320.jpg)
![Examples for computing GINI
C1 0
C2 6
C1 2
C2 4
C1 1
C2 5
P(C1) = 0/6 = 0 P(C2) = 6/6 = 1
Gini = 1 – P(C1)2
– P(C2)2
= 1 – 0 – 1 = 0
∑−=
j
tjptGINI 2
)]|([1)(
P(C1) = 1/6 P(C2) = 5/6
Gini = 1 – (1/6)2
– (5/6)2
= 0.278
P(C1) = 2/6 P(C2) = 4/6
Gini = 1 – (2/6)2
– (4/6)2
= 0.444](https://image.slidesharecdn.com/160301117-171130014410/85/Classification-Basic-Concepts-and-Decision-Trees-36-320.jpg)
Classification: Basic Concepts and Decision Trees
- 1. Classification: Basic Concepts and Decision Trees By SATHISHKUMAR G ([email protected]
- 3. Classification: Definition Given a collection of records (training set ) Each record contains a set of attributes, one of the attributes is the class. Find a model for class attribute as a function of the values of other attributes. Goal: previously unseen records should be assigned a class as accurately as possible. A test set is used to determine the accuracy of the model. Usually, the given data set is divided into training and test sets, with training set used to build the model and test set used to validate it.
- 5. Examples of Classification Task Predicting tumor cells as benign or malignant Classifying credit card transactions as legitimate or fraudulent Classifying secondary structures of protein as alpha-helix, beta-sheet, or random coil Categorizing news stories as finance, weather, entertainment, sports, etc
- 6. Classification Using Distance Place items in class to which they are “closest”. Must determine distance between an item and a class. Classes represented by Centroid: Central value. Medoid: Representative point. Individual points Algorithm: KNN
- 7. K Nearest Neighbor (KNN): Training set includes classes. Examine K items near item to be classified. New item placed in class with the most number of close items. O(q) for each tuple to be classified. (Here q is the size of the training set.)
- 8. KNN
- 9. Classification Techniques Decision Tree based Methods Rule-based Methods Memory based reasoning Neural Networks Naïve Bayes and Bayesian Belief Networks Support Vector Machines
- 10. Example of a Decision Tree Tid Refund Marital Status Taxable Income Cheat 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 No Single 90K Yes 10 categorical categorical continuous class Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Splitting Attributes Training Data Model: Decision Tree
- 11. Another Example of Decision Tree Tid Refund Marital Status Taxable Income Cheat 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 No Single 90K Yes 10 categorical categorical continuous class MarSt Refund TaxInc YESNO NO NO Yes No Married Single, Divorced < 80K > 80K There could be more than one tree that fits the same data!
- 12. Decision Tree Classification Task Decision Tree
- 13. Apply Model to Test Data Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data Start from the root of tree.
- 14. Apply Model to Test Data Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
- 15. Apply Model to Test Data Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
- 16. Apply Model to Test Data Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
- 17. Apply Model to Test Data Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
- 18. Apply Model to Test Data Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data Assign Cheat to “No”
- 19. Decision Tree Classification Task Decision Tree
- 20. Decision Tree Induction Many Algorithms: Hunt’s Algorithm (one of the earliest) CART ID3, C4.5 SLIQ,SPRINT
- 21. General Structure of Hunt’s Algorithm Let Dt be the set of training records that reach a node t General Procedure: If Dt contains records that belong the same class yt, then t is a leaf node labeled as yt If Dt is an empty set, then t is a leaf node labeled by the default class, yd If Dt contains records that belong to more than one class, use an attribute test to split the data into smaller subsets. Recursively apply the procedure to each subset. Tid Refund Marital Status Taxable Income Cheat 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 No Single 90K Yes 10 Dt ?
- 22. Hunt’s Algorithm Don’t Cheat Refund Don’t Cheat Don’t Cheat Yes No Refund Don’t Cheat Yes No Marital Status Don’t Cheat Cheat Single, Divorced Married Taxable Income Don’t Cheat < 80K >= 80K Refund Don’t Cheat Yes No Marital Status Don’t Cheat Cheat Single, Divorced Married
- 23. Tree Induction Greedy strategy. Split the records based on an attribute test that optimizes certain criterion. Issues Determine how to split the records How to specify the attribute test condition? How to determine the best split? Determine when to stop splitting
- 24. Tree Induction Greedy strategy. Split the records based on an attribute test that optimizes certain criterion. Issues Determine how to split the records How to specify the attribute test condition? How to determine the best split? Determine when to stop splitting
- 25. How to Specify Test Condition? Depends on attribute types Nominal Ordinal Continuous Depends on number of ways to split 2-way split Multi-way split
- 26. Splitting Based on Nominal Attributes Multi-way split: Use as many partitions as distinct values. Binary split: Divides values into two subsets. Need to find optimal partitioning. CarType Family Sports Luxury CarType {Family, Luxury} {Sports} CarType {Sports, Luxury} {Family} OR
- 27. Multi-way split: Use as many partitions as distinct values. Binary split: Divides values into two subsets. Need to find optimal partitioning. What about this split? Splitting Based on Ordinal Attributes Size Small Medium Large Size {Medium, Large} {Small} Size {Small, Medium} {Large} OR Size {Small, Large} {Medium}
- 28. Splitting Based on Continuous Attributes Different ways of handling Discretization to form an ordinal categorical attribute Static – discretize once at the beginning Dynamic – ranges can be found by equal interval bucketing, equal frequency bucketing (percentiles), or clustering. Binary Decision: (A < v) or (A ≥ v) consider all possible splits and finds the best cut can be more compute intensive
- 29. Splitting Based on Continuous Attributes
- 30. Tree Induction Greedy strategy. Split the records based on an attribute test that optimizes certain criterion. Issues Determine how to split the records How to specify the attribute test condition? How to determine the best split? Determine when to stop splitting
- 31. How to determine the Best Split Before Splitting: 10 records of class 0, 10 records of class 1 Which test condition is the best?
- 32. How to determine the Best Split Greedy approach: Nodes with homogeneous class distribution are preferred Need a measure of node impurity: Non-homogeneous, High degree of impurity Homogeneous, Low degree of impurity
- 33. Measures of Node Impurity Gini Index Entropy Misclassification error
- 34. How to Find the Best Split B? Yes No Node N3 Node N4 A? Yes No Node N1 Node N2 Before Splitting: C0 N10 C1 N11 C0 N20 C1 N21 C0 N30 C1 N31 C0 N40 C1 N41 C0 N00 C1 N01 M0 M1 M2 M3 M4 M12 M34 Gain = M0 – M12 vs M0 – M34
- 35. Measure of Impurity: GINI Gini Index for a given node t : (NOTE: p( j | t) is the relative frequency of class j at node t). Maximum (1 - 1/nc) when records are equally distributed among all classes, implying least interesting information Minimum (0.0) when all records belong to one class, implying most interesting information ∑−= j tjptGINI 2 )]|([1)( C1 0 C2 6 Gini= 0.000 C1 2 C2 4 Gini= 0.444 C1 3 C2 3 Gini= 0.500 C1 1 C2 5 Gini= 0.278
- 36. Examples for computing GINI C1 0 C2 6 C1 2 C2 4 C1 1 C2 5 P(C1) = 0/6 = 0 P(C2) = 6/6 = 1 Gini = 1 – P(C1)2 – P(C2)2 = 1 – 0 – 1 = 0 ∑−= j tjptGINI 2 )]|([1)( P(C1) = 1/6 P(C2) = 5/6 Gini = 1 – (1/6)2 – (5/6)2 = 0.278 P(C1) = 2/6 P(C2) = 4/6 Gini = 1 – (2/6)2 – (4/6)2 = 0.444
- 37. Splitting Based on GINI Used in CART, SLIQ, SPRINT. When a node p is split into k partitions (children), the quality of split is computed as, where, ni = number of records at child i, n = number of records at node p. ∑= = k i i split iGINI n n GINI 1 )(
- 38. Binary Attributes: Computing GINI Index Splits into two partitions Effect of Weighing partitions: Larger and Purer Partitions are sought for. B? Yes No Node N1 Node N2 Parent C1 6 C2 6 Gini = 0.500 N1 N2 C1 5 1 C2 2 4 Gini= 0.333 Gini(N1) = 1 – (5/6)2 – (2/6)2 = 0.194 Gini(N2) = 1 – (1/6)2 – (4/6)2 = 0.528 Gini(Children) = 7/12 * 0.194 + 5/12 * 0.528 = 0.333
- 39. Categorical Attributes: Computing Gini Index For each distinct value, gather counts for each class in the dataset Use the count matrix to make decisions CarType {Sports, Luxury} {Family} C1 3 1 C2 2 4 Gini 0.400 CarType {Sports} {Family, Luxury} C1 2 2 C2 1 5 Gini 0.419 CarType Family Sports Luxury C1 1 2 1 C2 4 1 1 Gini 0.393 Multi-way split Two-way split (find best partition of values)
- 40. Continuous Attributes: Computing Gini Index Use Binary Decisions based on one value Several Choices for the splitting value Number of possible splitting values = Number of distinct values Each splitting value has a count matrix associated with it Class counts in each of the partitions, A < v and A ≥ v Simple method to choose best v For each v, scan the database to gather count matrix and compute its Gini index Computationally Inefficient! Repetition of work.
- 41. Continuous Attributes: Computing Gini Index... For efficient computation: for each attribute, Sort the attribute on values Linearly scan these values, each time updating the count matrix and computing gini index Choose the split position that has the least gini index Cheat No No No Yes Yes Yes No No No No Taxable Income 60 70 75 85 90 95 100 120 125 220 55 65 72 80 87 92 97 110 122 172 230 <= > <= > <= > <= > <= > <= > <= > <= > <= > <= > <= > Yes 0 3 0 3 0 3 0 3 1 2 2 1 3 0 3 0 3 0 3 0 3 0 No 0 7 1 6 2 5 3 4 3 4 3 4 3 4 4 3 5 2 6 1 7 0 Gini 0.420 0.400 0.375 0.343 0.417 0.400 0.300 0.343 0.375 0.400 0.420 Split Positions Sorted Values
- 42. Alternative Splitting Criteria based on INFO Entropy at a given node t: (NOTE: p( j | t) is the relative frequency of class j at node t). Measures homogeneity of a node. Maximum (log nc) when records are equally distributed among all classes implying least information Minimum (0.0) when all records belong to one class, implying most information Entropy based computations are similar to the GINI index computations ∑−= j tjptjptEntropy )|(log)|()(
- 43. Examples for computing Entropy C1 0 C2 6 C1 2 C2 4 C1 1 C2 5 P(C1) = 0/6 = 0 P(C2) = 6/6 = 1 Entropy = – 0 log 0 – 1 log 1 = – 0 – 0 = 0 P(C1) = 1/6 P(C2) = 5/6 Entropy = – (1/6) log2 (1/6) – (5/6) log2 (1/6) = 0.65 P(C1) = 2/6 P(C2) = 4/6 Entropy = – (2/6) log2 (2/6) – (4/6) log2 (4/6) = 0.92 ∑−= j tjptjptEntropy )|(log)|()( 2
- 44. Splitting Based on INFO... Information Gain: Parent Node, p is split into k partitions; ni is number of records in partition i Measures Reduction in Entropy achieved because of the split. Choose the split that achieves most reduction (maximizes GAIN) Used in ID3 and C4.5 Disadvantage: Tends to prefer splits that result in large number of partitions, each being small but pure. −= ∑ = k i i split iEntropy n n pEntropyGAIN 1 )()(
- 45. Splitting Based on INFO... Gain Ratio: Parent Node, p is split into k partitions ni is the number of records in partition i Adjusts Information Gain by the entropy of the partitioning (SplitINFO). Higher entropy partitioning (large number of small partitions) is penalized! Used in C4.5 Designed to overcome the disadvantage of Information Gain SplitINFO GAIN GainRATIO Split split = ∑ = −= k i ii n n n n SplitINFO 1 log
- 46. Splitting Criteria based on Classification Error Classification error at a node t : Measures misclassification error made by a node. Maximum (1 - 1/nc) when records are equally distributed among all classes, implying least interesting information Minimum (0.0) when all records belong to one class, implying most interesting information )|(max1)( tiPtError i −=
- 47. Examples for Computing Error C1 0 C2 6 C1 2 C2 4 C1 1 C2 5 P(C1) = 0/6 = 0 P(C2) = 6/6 = 1 Error = 1 – max (0, 1) = 1 – 1 = 0 P(C1) = 1/6 P(C2) = 5/6 Error = 1 – max (1/6, 5/6) = 1 – 5/6 = 1/6 P(C1) = 2/6 P(C2) = 4/6 Error = 1 – max (2/6, 4/6) = 1 – 4/6 = 1/3 )|(max1)( tiPtError i −=
- 48. Comparison among Splitting Criteria For a 2-class problem:
- 49. Misclassification Error vs Gini A? Yes No Node N1 Node N2 Parent C1 7 C2 3 Gini = 0.42 N1 N2 C1 3 4 C2 0 3 Gini(N1) = 1 – (3/3)2 – (0/3)2 = 0 Gini(N2) = 1 – (4/7)2 – (3/7)2 = 0.489 Gini(Children) = 3/10 * 0 + 7/10 * 0.489 = 0.342
- 50. Tree Induction Greedy strategy. Split the records based on an attribute test that optimizes certain criterion. Issues Determine how to split the records How to specify the attribute test condition? How to determine the best split? Determine when to stop splitting
- 51. Stopping Criteria for Tree Induction Stop expanding a node when all the records belong to the same class Stop expanding a node when all the records have similar attribute values Early termination (to be discussed later)
- 52. Decision Tree Based Classification Advantages: Inexpensive to construct Extremely fast at classifying unknown records Easy to interpret for small-sized trees Accuracy is comparable to other classification techniques for many simple data sets
- 53. Example: C4.5 Simple depth-first construction. Uses Information Gain Sorts Continuous Attributes at each node. Needs entire data to fit in memory. Unsuitable for Large Datasets. Needs out-of-core sorting. You can download the software from: http://www.cse.unsw.edu.au/~quinlan/c4.5r8.tar.gz
- 54. Practical Issues of Classification Underfitting and Overfitting Missing Values Costs of Classification
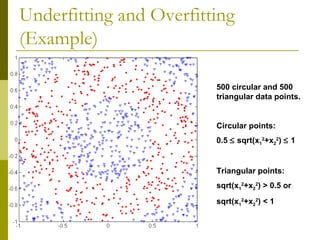
- 55. Underfitting and Overfitting (Example) 500 circular and 500 triangular data points. Circular points: 0.5 ≤ sqrt(x1 2 +x2 2 ) ≤ 1 Triangular points: sqrt(x1 2 +x2 2 ) > 0.5 or sqrt(x1 2 +x2 2 ) < 1
- 56. Underfitting and Overfitting Overfitting Underfitting: when model is too simple, both training and test errors are large
- 57. Overfitting due to Noise Decision boundary is distorted by noise point
- 58. Overfitting due to Insufficient Examples Lack of data points in the lower half of the diagram makes it difficult to predict correctly the class labels of that region - Insufficient number of training records in the region causes the decision tree to predict the test examples using other training records that are irrelevant to the classification task
- 59. Notes on Overfitting Overfitting results in decision trees that are more complex than necessary Training error no longer provides a good estimate of how well the tree will perform on previously unseen records Need new ways for estimating errors
- 60. Estimating Generalization Errors Re-substitution errors: error on training (Σ e(t) ) Generalization errors: error on testing (Σ e’(t)) Methods for estimating generalization errors: Optimistic approach: e’(t) = e(t) Pessimistic approach: For each leaf node: e’(t) = (e(t)+0.5) Total errors: e’(T) = e(T) + N × 0.5 (N: number of leaf nodes) For a tree with 30 leaf nodes and 10 errors on training (out of 1000 instances): Training error = 10/1000 = 1% Generalization error = (10 + 30×0.5)/1000 = 2.5% Reduced error pruning (REP): uses validation data set to estimate generalization error
- 61. Occam’s Razor Given two models of similar generalization errors, one should prefer the simpler model over the more complex model For complex models, there is a greater chance that it was fitted accidentally by errors in data Therefore, one should include model complexity when evaluating a model
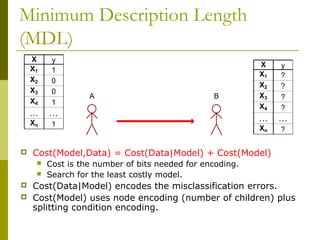
- 62. Minimum Description Length (MDL) Cost(Model,Data) = Cost(Data|Model) + Cost(Model) Cost is the number of bits needed for encoding. Search for the least costly model. Cost(Data|Model) encodes the misclassification errors. Cost(Model) uses node encoding (number of children) plus splitting condition encoding. A B X y X1 1 X2 0 X3 0 X4 1 … … Xn 1 X y X1 ? X2 ? X3 ? X4 ? … … Xn ?
- 63. How to Address Overfitting Pre-Pruning (Early Stopping Rule) Stop the algorithm before it becomes a fully-grown tree Typical stopping conditions for a node: Stop if all instances belong to the same class Stop if all the attribute values are the same More restrictive conditions: Stop if number of instances is less than some user-specified threshold Stop if class distribution of instances are independent of the available features (e.g., using χ2 test) Stop if expanding the current node does not improve impurity measures (e.g., Gini or information gain).
- 64. How to Address Overfitting… Post-pruning Grow decision tree to its entirety Trim the nodes of the decision tree in a bottom-up fashion If generalization error improves after trimming, replace sub-tree by a leaf node. Class label of leaf node is determined from majority class of instances in the sub-tree Can use MDL for post-pruning
- 65. Example of Post-Pruning A? A1 A2 A3 A4 Class = Yes 20 Class = No 10 Error = 10/30 Training Error (Before splitting) = 10/30 Pessimistic error = (10 + 0.5)/30 = 10.5/30 Training Error (After splitting) = 9/30 Pessimistic error (After splitting) = (9 + 4 × 0.5)/30 = 11/30 PRUNE! Class = Yes 8 Class = No 4 Class = Yes 3 Class = No 4 Class = Yes 4 Class = No 1 Class = Yes 5 Class = No 1
- 66. Examples of Post-pruning Optimistic error? Pessimistic error? Reduced error pruning? C0: 11 C1: 3 C0: 2 C1: 4 C0: 14 C1: 3 C0: 2 C1: 2 Don’t prune for both cases Don’t prune case 1, prune case 2 Case 1: Case 2: Depends on validation set
- 67. Handling Missing Attribute Values Missing values affect decision tree construction in three different ways: Affects how impurity measures are computed Affects how to distribute instance with missing value to child nodes Affects how a test instance with missing value is classified
- 68. Computing Impurity Measure Tid Refund Marital Status Taxable Income Class 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 ? Single 90K Yes 10 Class = Yes Class = No Refund=Yes 0 3 Refund=No 2 4 Refund=? 1 0 Split on Refund: Entropy(Refund=Yes) = 0 Entropy(Refund=No) = -(2/6)log(2/6) – (4/6)log(4/6) = 0.9183 Entropy(Children) = 0.3 (0) + 0.6 (0.9183) = 0.551 Gain = 0.9 × (0.8813 – 0.551) = 0.3303 Missing value Before Splitting: Entropy(Parent) = -0.3 log(0.3)-(0.7)log(0.7) = 0.8813
- 69. Distribute Instances Tid Refund Marital Status Taxable Income Class 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 Refund Yes No Class= Yes 0 Class= No 3 Cheat= Yes 2 Cheat= No 4 Refund Yes Tid Refund Marital Status Taxable Income Class 10 ? Single 90K Yes 10 No Class= Yes 2 + 6/ 9 Class= No 4 Probability that Refund=Yes is 3/9 Probability that Refund=No is 6/9 Assign record to the left child with weight = 3/9 and to the right child with weight = 6/9 Class= Yes 0 + 3/ 9 Class= No 3
- 70. Classify Instances Refund MarSt TaxInc YESNO NO NO Yes No Married Single, Divorced < 80K > 80K Married Single Divorce d Total Class=No 3 1 0 4 Class=Yes 6/9 1 1 2.67 Total 3.67 2 1 6.67 Tid Refund Marital Status Taxable Income Class 11 No ? 85K ? 10 New record: Probability that Marital Status = Married is 3.67/6.67 Probability that Marital Status ={Single,Divorced} is 3/6.67
- 71. Scalable Decision Tree Induction Methods SLIQ (EDBT’96 — Mehta et al.) Builds an index for each attribute and only class list and the current attribute list reside in memory SPRINT (VLDB’96 — J. Shafer et al.) Constructs an attribute list data structure PUBLIC (VLDB’98 — Rastogi & Shim) Integrates tree splitting and tree pruning: stop growing the tree earlier RainForest (VLDB’98 — Gehrke, Ramakrishnan & Ganti) Builds an AVC-list (attribute, value, class label) BOAT (PODS’99 — Gehrke, Ganti, Ramakrishnan & Loh) Uses bootstrapping to create several small samples
- 72. Thank you