combinational-circuit (1).pptx for all the digital electronics data
- 1. 1
- 2. ECB2212-Digital Electronics Numbering Systems Ms.K.Indra Gandhi Asst Prof (Sr.Gr) /ECE
- 3. Combinational Logic • Logic circuits for digital systems may be combinational or sequential. • A combinational circuit consists of input variables, logic gates, and output variables. 3
- 4. 4-2. Analysis procedure • To obtain the output Boolean functions from a logic diagram, proceed as follows: 1. Label all gate outputs that are a function of input variables with arbitrary symbols. Determine the Boolean functions for each gate output. 2. Label the gates that are a function of input variables and previously labeled gates with other arbitrary symbols. Find the Boolean functions for these gates. 4
- 5. 4-2. Analysis procedure 3. Repeat the process outlined in step 2 until the outputs of the circuit are obtained. 4. By repeated substitution of previously defined functions, obtain the output Boolean functions in terms of input variables. 5
- 6. Example F2 = AB + AC + BC; T1 = A + B + C; T2 = ABC; T3 = F2’T1; F1 = T3 + T2 F1 = T3 + T2 = F2’T1 + ABC = A’BC’ + A’B’C + AB’C’ + ABC 6
- 7. Derive truth table from logic diagram • We can derive the truth table in Table 4-1 by using the circuit of Fig.4-2. 7
- 8. 4-3. Design procedure 1. Table4-2 is a Code-Conversion example, first, we can list the relation of the BCD and Excess-3 codes in the truth table. 8
- 9. Karnaugh map 2. For each symbol of the Excess-3 code, we use 1’s to draw the map for simplifying Boolean function. 9
- 10. Circuit implementation z = D’; y = CD + C’D’ = CD + (C + D)’ x = B’C + B’D + BC’D’ = B’(C + D) + B(C + D)’ w = A + BC + BD = A + B(C + D) 10
- 11. 4-4. Binary Adder-Subtractor • A combinational circuit that performs the addition of two bits is called a half adder. • The truth table for the half adder is listed below: S = x’y + xy’ C = xy 11 S: Sum C: Carry
- 13. Full-Adder • One that performs the addition of three bits(two significant bits and a previous carry) is a full adder. 13
- 14. Simplified Expressions S = x’y’z + x’yz’ + xy’z’ + xyz C = xy + xz + yz 14 C
- 15. Full adder implemented in SOP 15
- 16. Another implementation • Full-adder can also implemented with two half adders and one OR gate (Carry Look-Ahead adder). S = z (x y) ⊕ ⊕ = z’(xy’ + x’y) + z(xy’ + x’y)’ = xy’z’ + x’yz’ + xyz + x’y’z C = z(xy’ + x’y) + xy = xy’z + x’yz + xy 16
- 17. Binary adder • This is also called Ripple Carry Adder ,because of the construction with full adders are connected in cascade. 17
- 18. Carry Propagation • Fig.4-9 causes a unstable factor on carry bit, and produces a longest propagation delay. • The signal from Ci to the output carry Ci+1, propagates through an AND and OR gates, so, for an n-bit RCA, there are 2n gate levels for the carry to propagate from input to output. 18
- 19. Carry Propagation • Because the propagation delay will affect the output signals on different time, so the signals are given enough time to get the precise and stable outputs. • The most widely used technique employs the principle of carry look-ahead to improve the speed of the algorithm. 19
- 20. Boolean functions Pi = Ai ⊕ Bi steady state value Gi = AiBi steady state value Output sum and carry Si = Pi ⊕ Ci Ci+1 = Gi + PiCi Gi : carry generate Pi : carry propagate C0 = input carry C1 = G0 + P0C0 C2 = G1 + P1C1 = G1 + P1G0 + P1P0C0 C3 = G2 + P2C2 = G2 + P2G1 + P2P1G0 + P2P1P0C0 • C3 does not have to wait for C2 and C1 to propagate. 20
- 21. Logic diagram of carry look-ahead generator • C3 is propagated at the same time as C2 and C1. 21
- 22. 4-bit adder with carry lookahead • Delay time of n-bit CLAA = XOR + (AND + OR) + XOR 22
- 23. Binary subtractor M = 1subtractor ; M = 0adder 23
- 24. Overflow • It is worth noting Fig.4-13 that binary numbers in the signed- complement system are added and subtracted by the same basic addition and subtraction rules as unsigned numbers. • Overflow is a problem in digital computers because the number of bits that hold the number is finite and a result that contains n+1 bits cannot be accommodated. 24
- 25. Overflow on signed and unsigned • When two unsigned numbers are added, an overflow is detected from the end carry out of the MSB position. • When two signed numbers are added, the sign bit is treated as part of the number and the end carry does not indicate an overflow. • An overflow cann’t occur after an addition if one number is positive and the other is negative. • An overflow may occur if the two numbers added are both positive or both negative. 25
- 26. 4-5 Decimal adder BCD adder can’t exceed 9 on each input digit. K is the carry. 26
- 27. Rules of BCD adder • When the binary sum is greater than 1001, we obtain a non-valid BCD representation. • The addition of binary 6(0110) to the binary sum converts it to the correct BCD representation and also produces an output carry as required. • To distinguish them from binary 1000 and 1001, which also have a 1 in position Z8, we specify further that either Z4 or Z2 must have a 1. C = K + Z8Z4 + Z8Z2 27
- 28. Implementation of BCD adder • A decimal parallel adder that adds n decimal digits needs n BCD adder stages. • The output carry from one stage must be connected to the input carry of the next higher-order stage. 28 If =1 0110
- 29. 4-6. Binary multiplier • Usually there are more bits in the partial products and it is necessary to use full adders to produce the sum of the partial products. 29 And
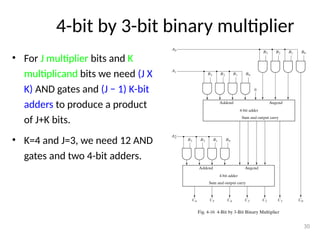
- 30. 4-bit by 3-bit binary multiplier • For J multiplier bits and K multiplicand bits we need (J X K) AND gates and (J − 1) K-bit adders to produce a product of J+K bits. • K=4 and J=3, we need 12 AND gates and two 4-bit adders. 30
- 31. 4-7. Magnitude comparator • The equality relation of each pair of bits can be expressed logically with an exclusive-NOR function as: A = A3A2A1A0 ; B = B3B2B1B0 xi=AiBi+Ai’Bi’ for i = 0, 1, 2, 3 (A = B) = x3x2x1x0 31
- 32. Magnitude comparator • We inspect the relative magnitudes of pairs of MSB. If equal, we compare the next lower significant pair of digits until a pair of unequal digits is reached. • If the corresponding digit of A is 1 and that of B is 0, we conclude that A>B. (A>B)= A3B’3+x3A2B’2+x3x2A1B’1+x3x2x1A0B’0 (A<B)= A’3B3+x3A’2B2+x3x2A’1B1+x3x2x1A’0B0 32
- 33. 4-8. Decoders • The decoder is called n-to-m-line decoder, where m≤2n . • the decoder is also used in conjunction with other code converters such as a BCD-to-seven_segment decoder. • 3-to-8 line decoder: For each possible input combination, there are seven outputs that are equal to 0 and only one that is equal to 1. 33
- 34. Implementation and truth table 34
- 35. Decoder with enable input • Some decoders are constructed with NAND gates, it becomes more economical to generate the decoder minterms in their complemented form. • As indicated by the truth table , only one output can be equal to 0 at any given time, all other outputs are equal to 1. 35
- 36. Demultiplexer • A decoder with an enable input is referred to as a decoder/demultiplexer. • The truth table of demultiplexer is the same with decoder. 36 Demultiplexer D0 D1 D2 D3 E A B
- 37. 3-to-8 decoder with enable implement the 4- to-16 decoder 37
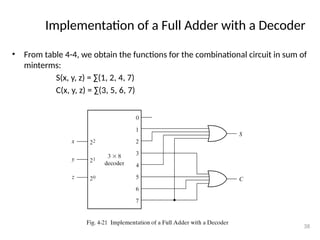
- 38. Implementation of a Full Adder with a Decoder • From table 4-4, we obtain the functions for the combinational circuit in sum of minterms: S(x, y, z) = ∑(1, 2, 4, 7) C(x, y, z) = ∑(3, 5, 6, 7) 38
- 39. 4-9. Encoders • An encoder is the inverse operation of a decoder. • We can derive the Boolean functions by table 4-7 z = D1 + D3 + D5 + D7 y = D2 + D3 + D6 + D7 x = D4 + D5 + D6 + D7 39
- 40. Priority encoder • If two inputs are active simultaneously, the output produces an undefined combination. We can establish an input priority to ensure that only one input is encoded. • Another ambiguity in the octal-to-binary encoder is that an output with all 0’s is generated when all the inputs are 0; the output is the same as when D0 is equal to 1. • The discrepancy tables on Table 4-7 and Table 4-8 can resolve aforesaid condition by providing one more output to indicate that at least one input is equal to 1. 40
- 41. Priority encoder V=0no valid inputs V=1valid inputs X’s in output columns represent don’t-care conditions X’s in the input columns are useful for representing a truth table in condensed form. Instead of listing all 16 minterms of four variables. 41
- 42. 4-input priority encoder • Implementation of table 4-8 x = D2 + D3 y = D3 + D1D’2 V = D0 + D1 + D2 + D3 42 0 0 0 0
- 43. 4-10. Multiplexers S = 0, Y = I0 Truth Table S Y Y = S’I0 + SI1 S = 1, Y = I1 0 I0 1 I1 43
- 45. Quadruple 2-to-1 Line Multiplexer • Multiplexer circuits can be combined with common selection inputs to provide multiple-bit selection logic. Compare with Fig4-24. 45 I0 I1 Y
- 46. Boolean function implementation • A more efficient method for implementing a Boolean function of n variables with a multiplexer that has n-1 selection inputs. F(x, y, z) = (1,2,6,7) 46
- 47. 4-input function with a multiplexer F(A, B, C, D) = (1, 3, 4, 11, 12, 13, 14, 15) 47
- 48. Three-State Gates • A multiplexer can be constructed with three-state gates. 48
- 49. 4-11. HDL for combinational circuits • A module can be described in any one of the following modeling techniques: 1. Gate-level modeling using instantiation of primitive gates and user-defined modules. 2. Dataflow modeling using continuous assignment statements with keyword assign. 3. Behavioral modeling using procedural assignment statements with keyword always. 49
- 50. Gate-level Modeling • A circuit is specified by its logic gates and their interconnection. • Verilog recognizes 12 basic gates as predefined primitives. • The logic values of each gate may be 1, 0, x(unknown), z(high-impedance). 50
- 51. Gate-level description on Verilog code The wire declaration is for internal connections. 51
- 52. • There are two basic types of design methodologies: top-down and bottom-up. • Top-down: the top-level block is defined and then the sub- blocks necessary to build the top-level block are identified. (Fig.4-9 binary adder) • Bottom-up: the building blocks are first identified and then combined to build the top-level block.(Example 4-2 4-bit adder) 52 Design methodologies
- 53. A bottom-up hierarchical description 53
- 54. Full-adder 54
- 55. 4-bit adder 55
- 56. Three state gates Gates statement: gate name(output, input, control) >> bufif1(OUT, A, control); A = OUT when control = 1, OUT = z when control = 0; >> notif0(Y, B, enable); Y = B’ when enable = 0, Y = z when enable = 1; 56
- 57. 2-to-1 multiplexer • HDL uses the keyword tri to indicate that the output has multiple drivers. module muxtri (A, B, select, OUT); input A,B,select; output OUT; tri OUT; bufif1 (OUT,A,select); bufif0 (OUT,B,select); endmodule 57
- 58. Dataflow modeling • It uses a number of operators that act on operands to produce desired results. Verilog HDL provides about 30 operator types. Table 4-10 Symbol Operation + binary addition − binary subtraction & bit-wise AND | bit-wise OR ^ bit-wise XOR ~ bit-wise NOT == equality > greater than < less than { } concatenation ?: conditional 58
- 59. Dataflow modeling • A continuous assignment is a statement that assigns a value to a net. • The data type net is used in Verilog HDL to represent a physical connection between circuit elements. • A net defines a gate output declared by an output or wire. 59
- 60. Dataflow description of 4-bit adder 60 HDL Example 4-4 //Dataflow description of 4-bit adder module binary_adder (A,B,Cin,SUM,Cout); input [3:0] A,B; input Cin; output [3:0] SUM; output Cout; assign {Cout,SUM} = A + B +Cin; endmodule
- 61. Data flow description of a 4-bit comparator 61
- 62. Dataflow description of 2-1 multiplexer • Conditional operator( ? : ) • Condition? true-expression : false-expression; 62
- 63. Behavioral modeling • It is used mostly to describe sequential circuits, but can be used also to describe combinational circuits. • Behavioral descriptions use the keyword always followed by a list of procedural assignment statements. • The target output of procedural assignment statements must be of the reg data type. Contrary to the wire data type, where the target output of an assignment may be continuously updated, a reg data type retains its value until a new value is assigned. 63
- 64. Behavioral description of 2-1 multiplexer 64
- 66. Writing a simple test bench • In addition to the always statement, test benches use the initial statement to provide stimulus to the circuit under test. • The always statement executes repeatedly in a loop. The initial statement executes only once starting from simulation time=0 and may continue with any operations that are delayed by a given number of time units as specified by the symbol #. For example: initial begin A = 0; B = 0; #10 A = 1; #20 A = 0; B = 1; end 66
- 67. Stimulus and design modules interaction • The signals of test bench as inputs to the design module are reg data type, the outputs of design module to test bench are wire data type. 67
- 68. Example 4-9 68
- 69. Gate Level of Verilog Code of Fig.4-2 69
- 70. Test Bench of the Figure 4-2 70

























































![Dataflow description of 4-bit adder
60
HDL Example 4-4
//Dataflow description of 4-bit adder
module binary_adder (A,B,Cin,SUM,Cout);
input [3:0] A,B;
input Cin;
output [3:0] SUM;
output Cout;
assign {Cout,SUM} = A + B +Cin;
endmodule](https://image.slidesharecdn.com/combinational-circuit1-240927072327-b8d44c01/85/combinational-circuit-1-pptx-for-all-the-digital-electronics-data-60-320.jpg)









