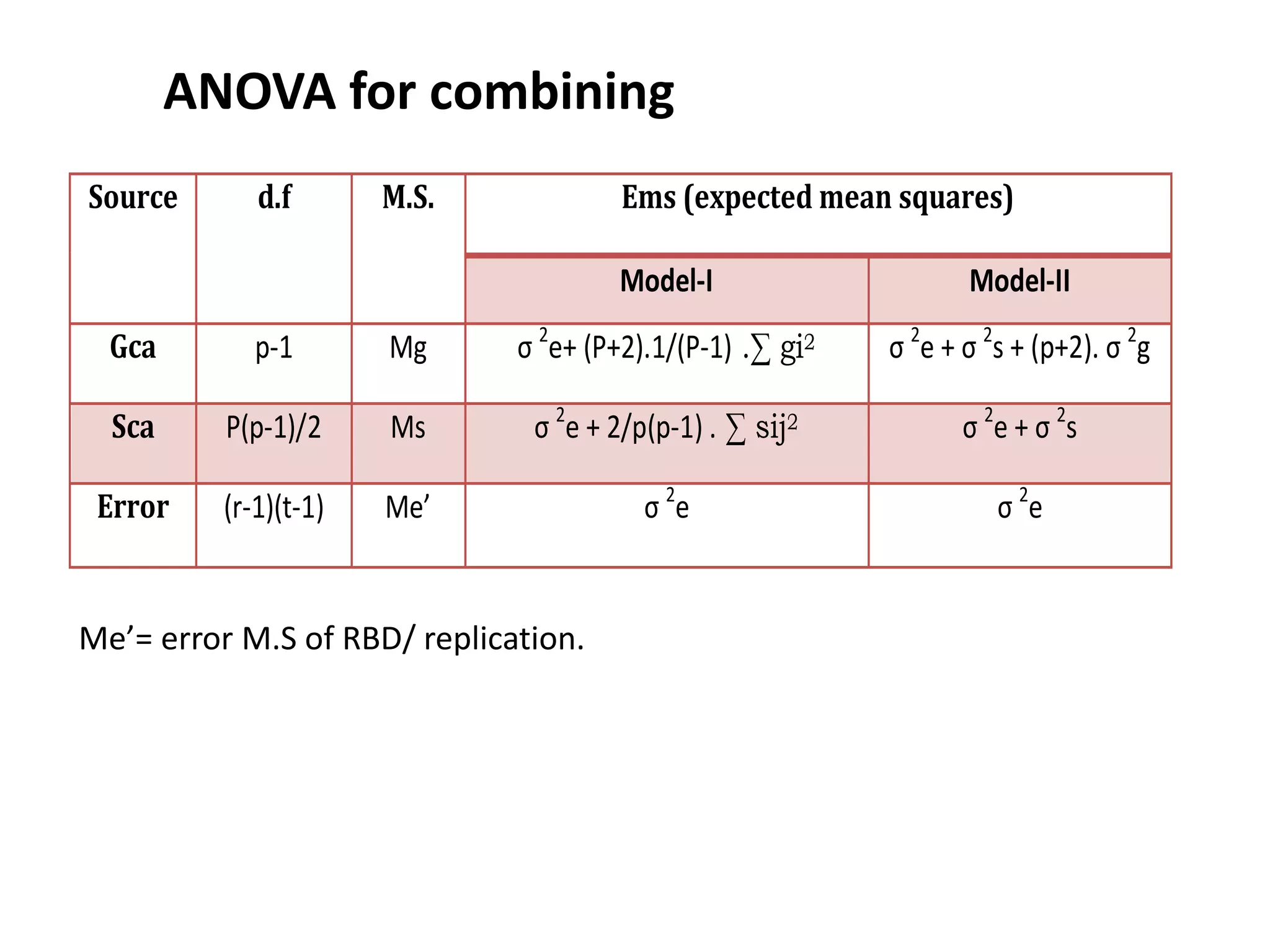
This document discusses combining ability analysis in plant breeding. It defines combining ability as the ability of a genotype to transmit superior performance in crosses. There are two types of combining ability: general combining ability (GCA), which is the average performance of a genotype in crosses, and specific combining ability (SCA), which is the performance in a specific cross. The document outlines methods to estimate GCA and SCA, including diallel crosses, and how this analysis can be used to select parents for hybridization and identify superior cross combinations.


















![• For combining ability analysis the replicated the data in
different treatments are to be arranged in a half matrix table
after arranging i.e. in this table each value is the mean value
of all the replications of a particular treatments.
Parents P1 2 3 4 5 6 7 Yi - Yij Yi +Yij
P1 11 12 13 14 15 16 17
2 22 23 24 25 26 27
3 33 34 35 36 37
4 44 45 46 47
5 55 56 57
6 66 67
7 77
Total Grand
total Y..
ability in method- II
Calculation of combining ability variances:
SS (gca) = 1/p+2 [ ∑(Yi + Yij)2 – 4/p Y2 ]
SS (sca)= ∑Yij2 -1/P+2 [∑(Yi + Yij)2] + 2/(p+1)(p+2) Y..2](https://image.slidesharecdn.com/combiningabilitystudyin5cropsankit-210330052322/75/Combining-ability-study-19-2048.jpg)





![• SS due to GCA = 1/p+2 [Σ (Yi.+Yii)2 - 4/p Y..2]
• = 1/10 [(124.17)2 +…+ (132.18)2 - 4/8
(486.08)2]
• = 80.09
• SS due to SCA = Σ Σ Yij2 -1/p+2 Σ ((Yi.+Yii)2 + 2/p +1)
(p+2) Y..2]
• = (14.00)2 +(13.83)2+…(12.20)2-1/10
[(124.17)2 +…+(132.18) 2 +2/9 x 10
(486.08)2
• = 390.3
• SS due to error = 34.89
• Analysis variance for combining ability
D.F S.S M.S Cal.F
GCA 7 80.09 11.44 22.971
SCA 28 390.3 13.94 27.992
ERROR 70 34.89 0.498](https://image.slidesharecdn.com/combiningabilitystudyin5cropsankit-210330052322/75/Combining-ability-study-26-2048.jpg)
![• Genetic components Model-I
• Σ g2i =Mg-M’e/(p+2) = 11.44- 0.498/10 = 1.09
• Σ s2ij =Ms-M’e = 13.94-0.498 = 13.442
• The ratio of Σ g2i / Σ s2ij =1.09/13.442= 0.08109
• Estimation of Genetic effects
• gi = 1/p+2 [(Yi.+Yii) - 2/p Y..]
• = 1/10[(124.17)-2/8 (486.08)]
• = -0.265 (Parent-1)
P1 P2 P3 P4 P5 P6 P7 P8
GCA
effect
0.265 -
2.178**
-0.239 0.397 0.511* -
0.796**
1** 1.092*
*](https://image.slidesharecdn.com/combiningabilitystudyin5cropsankit-210330052322/75/Combining-ability-study-27-2048.jpg)

![• Estimation of Genetic effects
• (2) SCA effects of hybrids
• Sij = Yij -1/p+2 ( Yi.+Yii +Yj.+Yjj) + 2/(p +1) (p+2) Y..]
• = P1x P2 -1/p+2 ( Y1+Y11 +Y2+Y22) + 2/(p +1) (p+2) Y..]
• = 13.83-1/10 (124.17+ 99.74) +2/90 (486.45)
• = 2.25(P1 xP2)
• =0.54(P1xP3)
• =2.124(P1XP4)…..](https://image.slidesharecdn.com/combiningabilitystudyin5cropsankit-210330052322/75/Combining-ability-study-29-2048.jpg)

















