compiler Design course material chapter 2

Rift Valley University Harar Campus
Computer Science Department
Compiler Design
Gadisa A.
Chapter two
Lexical analysis
1

Outline
 Introduction
 Interaction of Lexical Analyzer with Parser
 Token, pattern, lexeme
 Specification of patterns using regular expressions
 Regular expressions
 Regular expressions for tokens
 NFA and DFA
 Conversion from RE to NFA to DFA…
2

Introduction
 The role of lexical analyzer is:
• to read a sequence of characters from the source
program
• group them into lexemes and
• produce as output a sequence of tokens for each
lexeme in the source program.
 The scanner can also perform the following
secondary tasks:
 stripping out blanks, tabs, new lines
 stripping out comments
 keep track of line numbers (for error reporting)
3

4
Interaction of the Lexical Analyzer
with the Parser
lexical
analyzer
Syntax
analyzer
symbol
table
get next
token
token: smallest meaningful sequence of characters
of interest in source program
Source
Program
get next
char
next char next token
(Contains a record
for each identifier)

Token, pattern, lexeme
 A token is a sequence of characters from the source
program having a collective meaning.
 A token is a classification of lexical units.
- For example: id and num
 Lexemes are the specific character strings that make
up a token.
– For example: abc and 123A
 Patterns are rules describing the set of lexemes
belonging to a token.
– For example: “letter followed by letters and digits”
 Patterns are usually specified using regular expressions.
[a-zA-Z]*
Example: printf("Total = %dn", score);
5

Token, pattern, lexeme…
 Example: The following table shows some tokens and
their lexemes in Pascal (a high level, case insensitive
programming language)
Token Some lexemes pattern
begin Begin, Begin, BEGIN,
beGin…
Begin in small or capital
letters
if If, IF, iF, If If in small or capital letters
ident Distance, F1, x, Dist1,… Letters followed by zero or
more letters and/or digits
• In general, in programming languages, the following are
tokens:
keywords, operators, identifiers, constants, literals,
punctuation symbols…
6

Specification of patterns using
regular expressions
 Regular expressions
 Regular expressions for tokens
7

Regular expression: Definitions
 Represents patterns of strings of characters.
 An alphabet Σ is a finite set of symbols
(characters)
 A string s is a finite sequence of symbols
from Σ
 |s| denotes the length of string s
 ε denotes the empty string, thus |ε| = 0
 A language L is a specific set of strings over
some fixed alphabet Σ
8

Regular expressions…
 A regular expression is one of the following:
Symbol: a basic regular expression consisting of a single
character a, where a is from:
 an alphabet Σ of legal characters;
 the metacharacter ε: or
 the metacharacter ø.
 In the first case, L(a)={a};
 in the second case, L(ε)= {ε};
 in the third case, L(ø)= { }.
 {} – contains no string at all.
 {ε} – contains the single string consists of no character
9

Regular expressions…
 Alternation: an expression of the form r|s, where r
and s are regular expressions.
 In this case , L(r|s) = L(r) U L(s) ={r,s}
 Concatenation: An expression of the form rs, where r
and s are regular expressions.
 In this case, L(rs) = L(r)L(s)={rs}
 Repetition: An expression of the form r*, where r is a
regular expression.
 In this case, L(r*) = L(r)* ={ε, r,…}
10

Regular expression: Language Operations
 Union of L and M
 L ∪ M = {s |s ∈ L or s ∈ M}
 Concatenation of L and M
 LM = {xy | x ∈ L and y ∈ M}
 Exponentiation of L
 L0 = {ε}; Li = Li-1L
 Kleene closure of L
 L* = ∪i=0,…,∞ Li
 Positive closure of L
 L+ = ∪i=1,…,∞ Li
11
The following shorthands
are often used:
r+ =rr*
r* = r+| ε
r? =r|ε

12
RE’s: Examples
 L(01) = ?
 L(01|0) = ?
 L(0(1|0)) = ?
 Note order of precedence of operators.
 L(0*) = ?
 L((0|10)*(ε|1)) = ?

13
RE’s: Examples
 L(01) = {01}.
 L(01|0) = {01, 0}.
 L(0(1|0)) = {01, 00}.
 Note order of precedence of operators.
 L(0*) = {ε, 0, 00, 000,… }.
 L((0|10)*(ε|1)) = all strings of 0’s and 1’s
without two consecutive 1’s.

RE’s: Examples (more)
1- a | b = ?
2- (a|b)a = ?
3- (ab) | ε = ?
4- ((a|b)a)* = ?
 Reverse
1 – Even binary numbers =?
2 – An alphabet consisting of just three alphabetic
characters: Σ = {a, b, c}. Consider the set of all strings
over this alphabet that contains exactly one b.
14

RE’s: Examples (more)
1- a | b = {a,b}
2- (a|b)a = {aa,ba}
3- (ab) | ε ={ab, ε}
4- ((a|b)a)* = {ε, aa,ba,aaaa,baba,....}
 Reverse
1 – Even binary numbers (0|1)*0
2 – An alphabet consisting of just three alphabetic
characters: Σ = {a, b, c}. Consider the set of all strings
over this alphabet that contains exactly one b.
(a | c)*b(a|c)* {b, abc, abaca, baaaac, ccbaca, cccccb}
15

16
Regular Expressions (Summary)
 Definition: A regular expression is a string over
∑ if the following conditions hold:
1. ε, Ø, and a Є ∑ are regular expressions
2. If α and β are regular expressions, so is αβ
3. If α and β are regular expressions, so is α+β
4. If α is a regular expression, so is α*
5. Nothing else is a regular expression if it doesn’t
follow from (1) to (4)
 Let α be a regular expression, the language
represented by α is denoted by L(α).

Regular expressions for tokens
 Regular expressions are used to specify the
patterns of tokens.
 Each pattern matches a set of strings. It falls into
different categories:
 Reserved (Key) words: They are represented by
their fixed sequence of characters,
 Ex. if, while and do....
 If we want to collect all the reserved words into
one definition, we could write it as follows:
Reserved = if | while | do |...
17

Regular expressions for tokens…
 Special symbols: including arithmetic operators,
assignment and equality such as =, :=, +, -, *
 Identifiers: which are defined to be a sequence of
letters and digits beginning with letter,
 we can express this in terms of regular definitions as
follows:
letter = A|B|…|Z|a|b|…|z
digit = 0|1|…|9
or
letter= [a-zA-Z]
digit = [0-9]
identifiers = letter(letter|digit)*
18

 Numbers: Numbers can be:
 sequence of digits (natural numbers), or
 decimal numbers, or
 numbers with exponent (indicated by an e or E).
 Example: 2.71E-2 represents the number 0.0271.
 We can write regular definitions for these numbers as
follows:
nat = [0-9]+
signedNat = (+|-)? Nat
number = signedNat(“.” nat)?(E signedNat)?
 Literals or constants: which can include:
 numeric constants such as 42, and
 string literals such as “ hello, world”.
19

 relop  < | <= | = | <> | > | >=
 Comments: Ex. /* this is a C comment*/
 Delimiter  newline | blank | tab | comment
 White space = (delimiter )+
20

21
Automata
 Abstract machines
Characteristics
 Input: input values (from an input alphabet ∑) are applied
to the machine
 Output: outputs of the machine
 States: at any instant, the automation can be in one of
the several states
 State relation: the next state of the automation at any
instant is determined by the present state and the present
input

22
Automata: cont’d
 Types of automata
 Finite State Automata (FSA)
• Deterministic FSA (DFSA)
• Nondeterministic FSA (NFSA)
 Push Down Automata (PDA)
• Deterministic PDA (DPDA)
• Nondeterministic PDA (NPDA)

Finite Automata
 Finite State Automaton
Finite Automaton, Finite State Machine, FSA or FSM
 An abstract machine which can be used to
implement regular expressions (etc.).
 Has a finite number of states, and a finite amount
of memory (i.e., the current state).
 Can be represented by directed graphs or
transition tables
23

Finite-state Automata…
0 1 2 3 4  = { a, b, c }
a b c a
transition
final state
start state
state
• Representation
– An FSA may also be
represented with a
state-transition table.
The table for the
above FSA:
Input
State a b c
0 1  
1  2 
2   3
3 4  
4    24

Design of a Lexical Analyzer/Scanner
Finite Automata
 Lex – turns its input program into lexical analyzer.
 Finite automata are recognizers; they simply say "yes"
or "no" about each possible input string.
 Finite automata come in two flavors:
a) Nondeterministic finite automata (NFA) have no restrictions
on the labels of their edges.
ε, the empty string, is a possible label.
b) Deterministic finite automata (DFA) have, for each state,
and for each symbol of its input alphabet exactly one edge
with that symbol leaving that state.
25

Non-Deterministic Finite Automata
(NFA)
Definition
 An NFA M consists of five tuples: ( Σ,S, T, S0, F)
 A set of input symbols Σ, the input alphabet
 a finite set of states S,
 a transition function T: S × (Σ U { ε}) -> S (next state),
 a start state S0 from S, and
 a set of accepting/final states F from S.
 The language accepted by M, written L(M), is defined as:
The set of strings of characters c1c2...cn with each ci from
Σ U { ε} such that there exist states s1 in T(s0,c1), s2 in
T(s1,c2), ... , sn in T(sn-1,cn) with sn an element of F.
26

NFA…
 It is a finite automata which has choice of
edges
• The same symbol can label edges from one state to
several different states.
 An edge may be labeled by ε, the empty
string
• We can have transitions without any input
character consumption.
27

Transition Graph
 The transition graph for an NFA recognizing the
language of regular expression (a|b)*abb
28
0 1 2 3
start a
b
b b
S={0,1,2,3}
Σ={a,b}
S0=0
F={3}
a
all strings of a's and b's ending in the
particular string abb

Transition Table
 The mapping T of an NFA can be represented
in a transition table
29
State Input
a
Input
b
Input
ε
0 {0,1} {0} ø
1 ø {2} ø
2 ø {3} ø
3 ø ø ø
T(0,a) = {0,1}
T(0,b) = {0}
T(1,b) = {2}
T(2,b) = {3}
The language defined by an NFA is the set of input
strings it accepts, such as (a|b)*abb for the example
NFA

Acceptance of input strings by NFA
 An NFA accepts input string x if and only if there is
some path in the transition graph from the start
state to one of the accepting states
 The string aabb is accepted by the NFA:
30
0 0 1 2 3
a a b b
0 0 0 0 0
a a b b
YES
NO

31
Another NFA
start
a
b
a
b


An -transition is taken without consuming any character from
the input.
What does the NFA above accepts?
aa*|bb*

Deterministic Finite Automata (DFA)
 A deterministic finite automaton is a special
case of an NFA
 No state has an ε-transition
 For each state S and input symbol a there is at
most one edge labeled a leaving S
 Each entry in the transition table is a single state
 At most one path exists to accept a string
 Simulation algorithm is simple
32

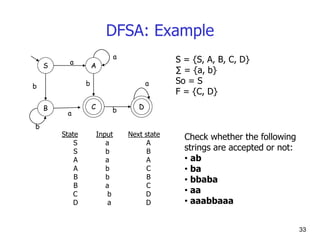
33
DFSA: Example
S
B C
b
a
a
A
D
a
b
b
b
a
S = {S, A, B, C, D}
∑ = {a, b}
So = S
F = {C, D}
State Input Next state
S a A
S b B
A a A
A b C
B b B
B a C
C b D
D a D
Check whether the following
strings are accepted or not:
• ab
• ba
• bbaba
• aa
• aaabbaaa

Design of a Lexical Analyzer Generator
Two algorithms:
1- Translate a regular expression into an NFA
(Thompson’s construction)
2- Translate NFA into DFA
(Subset construction)
34
Regular Expression DFA

From regular expression to an NFA
 It is known as Thompson’s construction.
Rules:
1- For an ε, a regular expressions, construct:
35
a
start

From regular expression to an NFA…
2- For a composition of regular expression:
 Case 1: Alternation: regular expression(s|r), assume
that NFAs equivalent to r and s have been
constructed.
36
36

From regular expression to an NFA…
 Case 2: Concatenation: regular expression sr
…r …s
ε
Case 3: Repetition r*
37

RENFADFA Minimize DFA states
 Step 1: Come up with a Regular Expression
(a|b)*ab
 Step 2: Use Thompson's construction to create
an NFA for that expression
38

RENFADFA Minimize DFA states
 Step 1: Come up with a Regular Expression
(a|b)*ab
 Step 2: Use Thompson's construction to create
an NFA for that expression
39

From RE to NFA:Exercises
 Construct NFA for token identifier.
letter(letter|digit)*
 Construct NFA for the following regular
expression:
(a|b)*abb
40

NFA for identifier: letter(letter|digit)*
41
0
6
4
5
3
2
1 7 8
start
letter ε
ε
ε
ε
ε
ε
ε
ε
letter
digit

NFA to a DFA…
Example: Convert the following NFA into the corresponding
DFA. letter (letter|digit)*
42
A
letter
B
D
C
digit
digit
digit
letter
letter
letter
start
A={0}
B={1,2,3,5,8}
C={4,7,2,3,5,8}
D={6,7,8,2,3,5}

Exercise: convert NFA of (a|b)*abb in to DFA.
43

compiler Design course material chapter 2

More Related Content

Similar to compiler Design course material chapter 2 (20)

More from gadisaAdamu (20)

Recently uploaded (20)

compiler Design course material chapter 2