![%{
#include <math.h> /* need this for the call to atof() below */
#include <stdio.h> /* need this for printf(), fopen() and stdin below */
%}
DIGIT [0-9]
ID [a-z][a-z0-9]*
%%
{DIGIT}+ {
printf("An integer: %s (%d)n", yytext,
atoi(yytext));
}
{DIGIT}+"."{DIGIT}* {
printf("A float: %s (%g)n", yytext,
atof(yytext));
}
if|then|begin|end|procedure|function {
printf("A keyword: %sn", yytext);
}
{ID} printf("An identifier: %sn", yytext);
"+"|"-"|"*"|"/" printf("An operator: %sn", yytext);
"{"[^}n]*"}" /* eat up one-line comments */
[ tn]+ /* eat up white space */
. printf("Unrecognized character: %sn", yytext);
%%
int main(int argc, char *argv[]){
++argv, --argc; /* skip over program name */
if (argc > 0)
yyin = fopen(argv[0], "r");
else
yyin = stdin;
yylex();
}](https://image.slidesharecdn.com/compilerdesignlexicalanalysis-250503120410-dd05356c/85/Compiler-Design_Lexical-Analysis-phase-pptx-54-320.jpg)
Compiler Design_Lexical Analysis phase.pptx
- 1. Unit 1: Lexical Analysis by Dr. R. A. Deshmukh
- 2. Contents • The role of the lexical analyzer • Specification of tokens • Finite state machines • From a regular expressions to an NFA • Convert NFA to DFA • Transforming grammars and regular expressions • Transforming automata to grammars • Language for specifying lexical analyzers
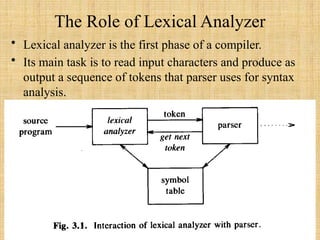
- 3. The Role of Lexical Analyzer • Lexical analyzer is the first phase of a compiler. • Its main task is to read input characters and produce as output a sequence of tokens that parser uses for syntax analysis.
- 4. Issues in Lexical Analysis • There are several reasons for separating the analysis phase of compiling into lexical analysis and parsing: – Simpler design – Compiler efficiency – Compiler portability • Specialized tools have been designed to help automate the construction of lexical analyzer and parser when they are separated.
- 5. Tokens, Patterns, Lexemes • A lexeme is a sequence of characters in the source program that is matched by the pattern for a token. • A lexeme is a basic lexical unit of a language comprising one or several words, the elements of which do not separately convey the meaning of the whole. • The lexemes of a programming language include its identifier, literals, operators, and special words. • A token of a language is a category of its lexemes. • A pattern is a rule describing the set of lexemes that can represent as particular token in source program.
- 6. Examples of Tokens const pi = 3.1416; The substring pi is a lexeme for the token “identifier.”
- 7. Lexeme and Token semicolon ; int_literal 17 plus_op + identifier Count multi_op * int_literal 2 equal_sign = Identifier Index Tokens Lexemes Index = 2 * count +17;
- 8. Lexical Errors • Few errors are discernible at the lexical level alone, because a lexical analyzer has a very localized view of a source program. • Let some other phase of compiler handle any error. • Panic mode • Error recovery
- 10. ab3++ id -> l (l|d)* ab3 id ++ unary op a<=b
- 12. Specification of Tokens • Regular expressions are an important notation for specifying patterns. • Operation on languages • Regular expressions • Regular definitions • Notational shorthands
- 13. • Alphabet {0,1} • String 0110 • Language {0,10,00,110, ….} • Prefix: • abc => {epsilon, abc, ab, a} • Proper prefix: abc => {epsilon, ab, a} • Suffix: • abc => {epsilon, abc,bc,c} • Proper suffix: abc => {epsilon, bc,c}
- 15. Regular Expressions • Regular expression is a compact notation for describing string. • In Pascal, an identifier is a letter followed by zero or more letter or digits letter(letter|digit)* • |: or • *: zero or more instance of • a(a|d)*
- 16. Rules • is a regular expression that denotes {}, the set containing empty string. • If a is a symbol in , then a is a regular expression that denotes {a}, the set containing the string a. • Suppose r and s are regular expressions denoting the language L(r) and L(s), then – (r) |(s) is a regular expression denoting L(r)L(s). – (r)(s) is regular expression denoting L (r) L(s). – (r) * is a regular expression denoting (L (r) )*. – (r) is a regular expression denoting L (r).
- 17. Precedence Conventions • The unary operator * has the highest precedence and is left associative. • Concatenation has the second highest precedence and is left associative. • | has the lowest precedence and is left associative. • (a)|(b)*(c)a|b*c
- 18. Example of Regular Expressions
- 19. Properties of Regular Expression
- 20. Regular Definitions • If is an alphabet of basic symbols, then a regular definition is a sequence of definitions of the form: d1r1 d2r2 ... dnrn • where each di is a distinct name, and each ri is a regular expression over the symbols in {d1,d2, …,di-1}, i.e., the basic symbols and the previously defined names.
- 21. Examples of Regular Definitions Example 3.5. Unsigned numbers 32 45.56 67.7E+2, 78E-2, 6.5E3
- 22. Notational Shorthands ? r? -> r | e a ?
- 23. Finite Automata • A recognizer for a language is a program that takes as input a string x and answer “yes” if x is a sentence of the language and “no” otherwise. • We compile a regular expression into a recognizer by constructing a generalized transition diagram called a finite automaton. • A finite automaton can be deterministic or nondeterministic, where nondeterministic means that more than one transition out of a state may be possible on the same input symbol.
- 24. Nondeterministic Finite Automata (NFA) • A set of states S • A set of input symbols • A transition function move that maps state- symbol pairs to sets of states • A state s0 that is distinguished as the start (initial) state • A set of states F distinguished as accepting (final) states.
- 25. NFA • An NFA can be represented diagrammatically by a labeled directed graph, called a transition graph, in which the nodes are the states and the labeled edges represent the transition function. • (a|b)*abb
- 26. NFA Transition Table • The easiest implementation is a transition table in which there is a row for each state and a column for each input symbol and , if necessary.
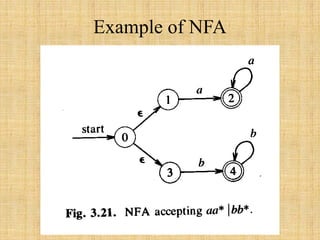
- 27. Example of NFA
- 28. Deterministic Finite Automata (DFA) • A DFA is a special case of a NFA in which – no state has an -transition – for each state s and input symbol a, there is at most one edge labeled a leaving s.
- 29. Simulating a DFA
- 30. Example of DFA
- 31. Conversion of an NFA into DFA • Subset construction algorithm is useful for simulating an NFA by a computer program. • In the transition table of an NFA, each entry is a set of states; in the transition table of a DFA, each entry is just a single state. • The general idea behind the NFA-to-DFA construction is that each DFA state corresponds to a set of NFA states. • The DFA uses its state to keep track of all possible states the NFA can be in after reading each input symbol.
- 32. Subset Construction - constructing a DFA from an NFA • Input: An NFA N. • Output: A DFA D accepting the same language. • Method: We construct a transition table Dtran for D. Each DFA state is a set of NFA states and we construct Dtran so that D will simulate “in parallel” all possible moves N can make on a given input string.
- 33. Subset Construction (II) s represents an NFA state T represents a set of NFA states.
- 35. Subset Construction (IV) (ε-closure computation)
- 36. Example
- 37. Example (II)
- 38. Example (III)
- 39. Minimizing the number of states in DFA • Minimize the number of states of a DFA by finding all groups of states that can be distinguished by some input string. • Each group of states that cannot be distinguished is then merged into a single state. • Algorithm 3.6 Aho page 142
- 40. Minimizing the number of states in DFA (II)
- 41. Construct New Partition An example in class
- 42. From Regular Expression to NFA • Thompson’s construction - an NFA from a regular expression • Input: a regular expression r over an alphabet . • Output: an NFA N accepting L(r)
- 43. Method • First parse r into its constituent subexpressions. • Construct NFA’s for each of the basic symbols in r. – for – for a in
- 44. Method (II) • For the regular expression s|t, • For the regular expression st,
- 45. Method (III) • For the regular expression s*, • For the parenthesized regular expression (s), use N(s) itself as the NFA. Every time we construct a new state, we give it a distinct name.
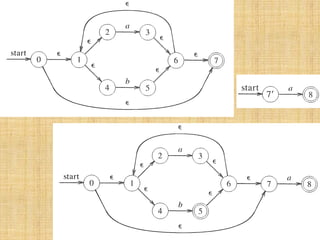
- 46. Example - construct N(r) for r=(a|b)*abb
- 47. Example (II)
- 48. Example (III)
- 49. Regular Expressions Grammars More in class …
- 50. Grammars Regular Expressions More in class …
- 51. Automata Grammars More in class …
- 52. A Language for Specifying Lexical Analyzer yylex()
- 53. Simple Lex Example int num_lines = 0, num_chars = 0; %% n ++num_lines; ++num_chars; . ++num_chars; %% main() { yylex(); printf( "# of lines = %d, # of chars = %dn", num_lines, num_chars ); }
- 54. %{ #include <math.h> /* need this for the call to atof() below */ #include <stdio.h> /* need this for printf(), fopen() and stdin below */ %} DIGIT [0-9] ID [a-z][a-z0-9]* %% {DIGIT}+ { printf("An integer: %s (%d)n", yytext, atoi(yytext)); } {DIGIT}+"."{DIGIT}* { printf("A float: %s (%g)n", yytext, atof(yytext)); } if|then|begin|end|procedure|function { printf("A keyword: %sn", yytext); } {ID} printf("An identifier: %sn", yytext); "+"|"-"|"*"|"/" printf("An operator: %sn", yytext); "{"[^}n]*"}" /* eat up one-line comments */ [ tn]+ /* eat up white space */ . printf("Unrecognized character: %sn", yytext); %% int main(int argc, char *argv[]){ ++argv, --argc; /* skip over program name */ if (argc > 0) yyin = fopen(argv[0], "r"); else yyin = stdin; yylex(); }