compression & huffman coder problem .ppt
- 1. Compression & Huffman Codes
- 2. Compression Definition Reduce size of data (number of bits needed to represent data) Benefits Reduce storage needed Reduce transmission cost / latency / bandwidth
- 3. Sources of Compressibility Redundancy Recognize repeating patterns Exploit using Dictionary Variable length encoding Human perception Less sensitive to some information Can discard less important data
- 4. Types of Compression Lossless Preserves all information Exploits redundancy in data Applied to general data Lossy May lose some information Exploits redundancy & human perception Applied to audio, image, video
- 5. Effectiveness of Compression Metrics Bits per byte (8 bits) 2 bits / byte ¼ original size 8 bits / byte no compression Percentage 75% compression ¼ original size
- 6. Effectiveness of Compression Depends on data Random data hard Example: 1001110100 ? Organized data easy Example: 1111111111 110 Corollary No universally best compression algorithm
- 7. Effectiveness of Compression Lossless Compression is not always possible If compression is always possible (alternative view) Compress file (reduce size by 1 bit) Recompress output Repeat (until we can store data with 0 bits)
- 8. Lossless Compression Techniques LZW (Lempel-Ziv-Welch) compression Build pattern dictionary Replace patterns with index into dictionary Run length encoding Find & compress repetitive sequences Huffman codes Use variable length codes based on frequency
- 9. Huffman Code Approach Variable length encoding of symbols Exploit statistical frequency of symbols Efficient when symbol probabilities vary widely Principle Use fewer bits to represent frequent symbols Use more bits to represent infrequent symbols A A B A A A A B
- 10. Huffman Code Example Expected size Original 1/82 + 1/42 + 1/22 + 1/82 = 2 bits / symbol Huffman 1/83 + 1/42 + 1/21 + 1/83 = 1.75 bits / symbol Symbol A B C D Frequency 13% 25% 50% 12% Original Encoding 00 01 10 11 2 bits 2 bits 2 bits 2 bits Huffman Encoding 110 10 0 111 3 bits 2 bits 1 bit 3 bits
- 11. Huffman Code Data Structures Binary (Huffman) tree Represents Huffman code Edge code (0 or 1) Leaf symbol Path to leaf encoding Example A = “110”, B = “10”, C = “0” Priority queue To efficiently build binary tree 1 1 0 0 D C B A 0 1
- 12. Huffman Code Algorithm Overview Encoding Calculate frequency of symbols in file Create binary tree representing “best” encoding Use binary tree to encode compressed file For each symbol, output path from root to leaf Size of encoding = length of path Save binary tree
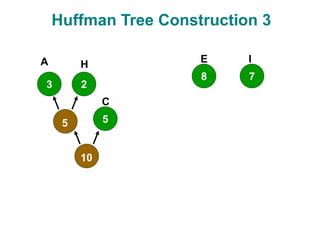
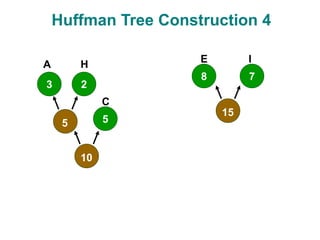
- 13. Huffman Code – Creating Tree Algorithm Place each symbol in leaf Weight of leaf = symbol frequency Select two trees L and R (initially leafs) Such that L, R have lowest frequencies in tree Create new (internal) node Left child L Right child R New frequency frequency( L ) + frequency( R ) Repeat until all nodes merged into one tree
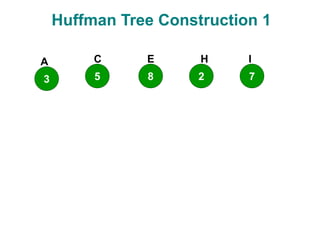
- 14. Huffman Tree Construction 1 3 5 8 2 7 A C E H I
- 15. Huffman Tree Construction 2 3 5 8 2 7 5 A C E H I
- 16. Huffman Tree Construction 3 3 5 8 2 7 5 10 A C E H I
- 17. Huffman Tree Construction 4 3 5 8 2 7 5 10 15 A C E H I
- 18. Huffman Tree Construction 5 3 5 8 2 7 5 10 15 25 1 1 1 1 0 0 0 0 A C E H I E = 01 I = 00 C = 10 A = 111 H = 110
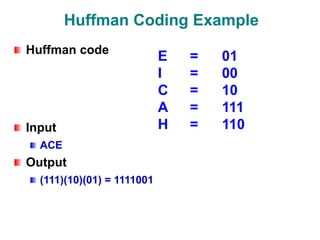
- 19. Huffman Coding Example Huffman code Input ACE Output (111)(10)(01) = 1111001 E = 01 I = 00 C = 10 A = 111 H = 110
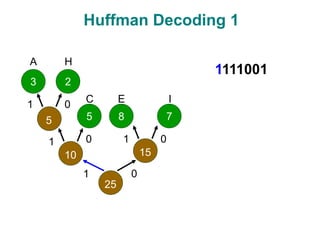
- 20. Huffman Code Algorithm Overview Decoding Read compressed file & binary tree Use binary tree to decode file Follow path from root to leaf
- 21. Huffman Decoding 1 3 5 8 2 7 5 10 15 25 1 1 1 1 0 0 0 0 A C E H I 1111001
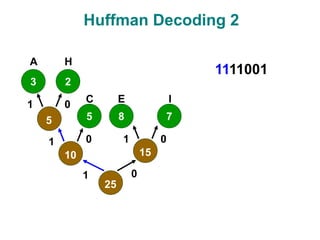
- 22. Huffman Decoding 2 3 5 8 2 7 5 10 15 25 1 1 1 1 0 0 0 0 A C E H I 1111001
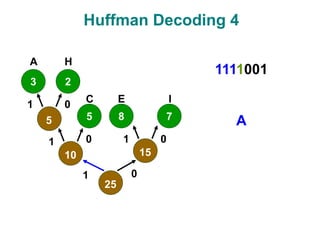
- 23. Huffman Decoding 3 3 5 8 2 7 5 10 15 25 1 1 1 1 0 0 0 0 A C E H I 1111001 A
- 24. Huffman Decoding 4 3 5 8 2 7 5 10 15 25 1 1 1 1 0 0 0 0 A C E H I 1111001 A
- 25. Huffman Decoding 5 3 5 8 2 7 5 10 15 25 1 1 1 1 0 0 0 0 A C E H I 1111001 AC
- 26. Huffman Decoding 6 3 5 8 2 7 5 10 15 25 1 1 1 1 0 0 0 0 A C E H I 1111001 AC
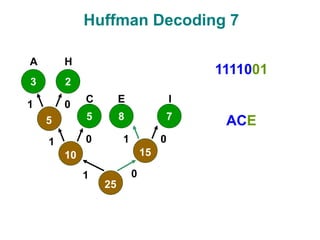
- 27. Huffman Decoding 7 3 5 8 2 7 5 10 15 25 1 1 1 1 0 0 0 0 A C E H I 1111001 ACE
- 28. Huffman Code Properties Prefix code No code is a prefix of another code Example Huffman(“I”) 00 Huffman(“X”) 001 // not legal prefix code Can stop as soon as complete code found No need for end-of-code marker Nondeterministic Multiple Huffman coding possible for same input If more than two trees with same minimal weight
- 29. Huffman Code Properties Greedy algorithm Chooses best local solution at each step Combines 2 trees with lowest frequency Still yields overall best solution Optimal prefix code Based on statistical frequency Better compression possible (depends on data) Using other approaches (e.g., pattern dictionary)