Computer Graphics - Lecture 03 - Virtual Cameras and the Transformation Pipeline

Virtual Cameras
and
The Transformation Pipeline
Anton Gerdelan
gerdela@scss.tcd.ie
with content from
Rachel McDonnell
13 Oct 2014

Virtual Camera
●
We want to navigate through our scene in 3d
●
Solution = create a transformation pipeline
●
Move all points relative to some arbitrary view point,
such that the view point is the new (0,0,0) origin
●
Also project our scene with a perspective rather than
orthogonal view

Transformation Pipeline – Coordinate Spaces
* model
matrix
* view
matrix
vertex shader output
* projection
matrix
perspective
division
(x,y,z) / w

Transformation Pipeline – Coordinate Spaces
* model
matrix
* view
matrix
vertex shader output
perspective
division
(x,y,z) / w
* projection
matrix
? ?
?

Local Space
●
When you create a triangle or
●
Load a mesh from a file
●
Has some (0,0,0) origin, local to that particular mesh
●
Translate, rotate, scale to position in a virtual world
– Multiply points with a model matrix aka “world matrix”
– mat4 M = T * R * S;
vec4 pos_wor = M * vec4 (pos_loc, 1.0);

World Space
●
Objects positioned in scene or “virtual world”
●
Has a world (0,0,0) origin
●
Can get distances between objects
●
Now we want to show the view from a camera, moving through the virtual
world
●
Multiply world space points by a view matrix to get to eye space
mat4 V = R * T; // inverse of cam pos & angle
mat4 V = lookAt (vec3 pos, vec3 target, vec3 up);
vec4 pos_eye = M * pos_wor;

View Matrix
Right xyz
Up xyz
-Forward xyz
-Position xyz
Careful now!

lookAt(vec3 eye, vec3 look, vec3 up)
●
Typical maths library
function
●
Returns mat4
●
Sets camera position
●
Point at target
●
Careful with “up” unit vector
●
Not ideal for full 3d rotation

●
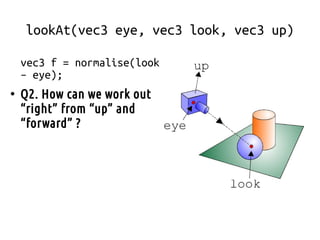
Rem: view matrix needs
– Right
– Forward
– Up
– Position
●
(set of 3d vectors)
●
Q1: How can we work
out “forward”?

vec3 f = normalise(look
– eye);
●
Q2. How can we work out
“right” from “up” and
“forward” ?

lookAt()
vec3 r = cross(f, up);
// recalc up to be sure
vec3 u = normalise (cross (r, f));
mat4 T = translate (-eye);
mat4 R = plug-in r,u,-f
return R * T;
●
Q3. Why did I re-calculate “up”?
●
Q4. What would happen if I did cross(up, f)
instead?
●
Q5. What must you do if camera pitches up/down?

Q1. What is the cross product of these vectors?
[0.0, 0.0, 1.0] X [1.0, 0.0, 0.0]
Q2. How do you normalise a 4d vector?
[10.0, 0.0, 0.0, 0.0]

Rotation Method Limitations
●
Calculating from fixed-axis X*Y*Z
rotation matrices
●
LookAt() is good for panning,
not great for flight sims
●
quaternions better suited to
creating rotation matrix with full
3d rotation
– Euler axis & angle in 4 numbers
– then some multiplications to get a
4X4 rotation matrix
– Good for local pitch/yaw/roll
Arbitrary “Euler axis”

Eye Space
●
Objects positioned relative to view point and direction
●
Has an eye origin (0, 0, 0)
●
Our view area is still -1 to 1 on XYZ.
●
Our view is still a parallel (orthogonal/orthographic)
projection.
●
Q. How can we manipulate the projection?

What We Have Now
Q. How can we make our view cover more of the scene?

Orthographic Projection Matrix
Q. What affine matrices does this look similar to?
Zi -
Zi + Zf
Zf - Zi

Computer Graphics - Lecture 03 - Virtual Cameras and the Transformation Pipeline

How can we approximate a cone of view?
●
Has to map to a 2d rectangular view, not a circle
(well...we could do a circle)
●
Has to have minimum and maximum cut-of distances
●
Some sort of angle of view
●
We had a cuboid before for orthographic
●
Q. What 3d geometric shape is this?

Typical Perspective Function
mat4 perspective (
float fovy,
float aspect,
float zNear,
float zFar
);
●
Fovy is “field of view y-axis”
– angle from horizon to top
– convert to radians
●
Aspect ratio is
(float)width / (float)height
of viewport
●
Near and far are “clip
planes”
– 0.1 and 1000.0 are typical

A Symmetric Perspective Matrix
●
Q. An aspect of 2.0 means?
●
Wrong aspect = distortion
●
Depth bufer precision
(ranges of z) has only so many
bits per pixel.
●
Smaller zFar / zNear ratio =
more precision
●
As zNear -> 0, zFar -> infinity
– Do not make zNear = 0.0
1.0 / tan (fovy * 0.5);
???

FOV
●
Beware comparisons of angle of view
●
Older games etc. used horizontal angles of view ~90
degrees
●
These also had fixed-aspect displays:
– 320x200 (2.5:4)
– 320x240, 640x480, etc. -> (3:4) = 1.3333...
●
LookAt() etc. Use vertical angles
– 90 degrees horiz. / 1.333333 = 67.5 degrees vert.

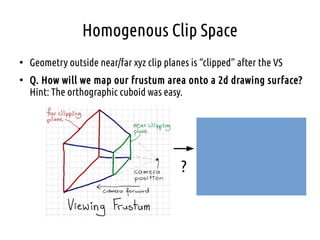
Homogenous Clip Space
●
Geometry outside near/far xyz clip planes is “clipped” after the VS
●
Q. How will we map our frustum area onto a 2d drawing surface?
Hint: The orthographic cuboid was easy.
?

Perspective Division
A. We will squish in the large back end until it is a -1 to 1 XYZ
box.
Q. How? Hint: Some of you did this in Assignment 0

Perspective Division
●
Vertex shader output is a 4d variable
gl_Position = P * V * M * vec4 (vp, 1.0);
gl_Position = vec4 (x, y, z, w);
●
After the VS, a built-in mechanism does
position = vec3 (gl_Position.xyz / gl_Position.w);
●
Q. What does the perspective matrix do to w?

Normalised Device Space
●
All coordinates are between -1 and 1 – the unit cube
●
This is very easy to scale by # pixels wide and high
●
Project to 2d
●
Front/back face select and cull if enabled
●
Rasterise to pixels/fragments

Typical Vertex Shader w/ Camera
#version 400
in vec3 vertex_point, vertex_normal;
uniform mat4 P, V, M;
out vec3 p_eye, n_eye;
void main () {
gl_Position = P * V * M * vec4 (vertex_point, 1.0);
p_eye = V * M * vec4 (vertex_point, 1.0);
n_eye = V * M * vec4 (vertex_normal, 0.0);
}
●
Order of multiplication is fundamentally important
●
Never compare variables from diferent coordinate spaces
●
Use a postfix or prefix naming convention for variables
useful for
lighting

Depth Testing (automatic step)
and The Depth Bufer
●
Edwin Catmull again – PhD thesis 1974, U. Utah.
●
Whenever we write a fragment it writes the colour to the
framebufer's colour bufer (a big 2d image)
●
But first...if depth testing is enabled
●
It checks another 2d image called the depth bufer
●
If its own depth is smaller/closer it overwrites both the depth and
colour bufer pixels
●
Q. What does this do?
●
Can we disable the depth testing and try?

Depth Bufer
Smaller value = farther
away
Bigger = closer
In F.Shader use built-in gl_FragCoord.w to get
this value and use as a colour

Reading List and Practical Tasks
●
Shirley & Marschner – “Fundamentals” Ch. 7 “Viewing”
●
Akenine Moeller et. al “Real-Time Rendering” Ch. 2 and
4.6 “Projections” (very good)
●
Know how to work out the pipeline by hand on paper for
1 vertex & M, V, and P
●
Hint: add a “print_matrix(m)” function to check contents

3rd
Assignment - Viewing
●
Due next week!
●
Start way ahead of time
(easy to get into a transformations mess)
●
If you finish early, get a head start on game project skills:
– Play
– Upgrade – Load a mesh? Full 3d camera controls?
– make all the mistakes
– ask for advice now (discussion boards)

Computer Graphics - Lecture 03 - Virtual Cameras and the Transformation Pipeline

More Related Content

What's hot (20)

Similar to Computer Graphics - Lecture 03 - Virtual Cameras and the Transformation Pipeline (20)

Recently uploaded (20)

Computer Graphics - Lecture 03 - Virtual Cameras and the Transformation Pipeline