Computer Vision Computer Vision: Algorithms and Applications Richard Szeliski

Dimensionality Reduction
• PCA, ICA, LLE, Isomap,
Autoencoder
• PCA is the most important technique to
know. It takes advantage of correlations in
data dimensions to produce the best possible
lower dimensional representation based on
linear projections (minimizes reconstruction
error).
• PCA should be used for dimensionality
reduction, not for discovering patterns or
making predictions. Don't try to assign
semantic meaning to the bases.

• http://fakeisthenewreal.org/reform/

Clustering example: image segmentation
Goal: Break up the image into meaningful or perceptually
similar regions

Segmentation for feature support or efficiency
[Felzenszwalb and Huttenlocher 2004]
[Hoiem et al. 2005, Mori 2005]
[Shi and Malik 2001]
Slide: Derek Hoiem
50x50
Patch
50x50
Patch

Segmentation as a result
Rother et al. 2004

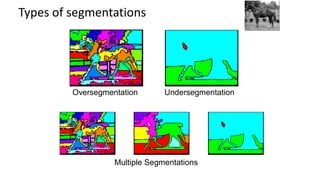
Types of segmentations
Oversegmentation Undersegmentation
Multiple Segmentations

Clustering: group together similar points and represent them
with a single token
Key Challenges:
1) What makes two points/images/patches similar?
2) How do we compute an overall grouping from pairwise similarities?
Slide: Derek Hoiem

How do we cluster?
• K-means
– Iteratively re-assign points to the nearest cluster center
• Agglomerative clustering
– Start with each point as its own cluster and iteratively merge the closest
clusters
• Mean-shift clustering
– Estimate modes of pdf
• Spectral clustering
– Split the nodes in a graph based on assigned links with similarity weights

Clustering for Summarization
Goal: cluster to minimize variance in data given clusters
– Preserve information
 
 

N
j
K
i
j
i
N ij
2
1
,
*
*
argmin
, x
c
δ
c
δ
c

Whether xj is assigned to ci
Cluster center Data
Slide: Derek Hoiem

K-means algorithm
Illustration: http://en.wikipedia.org/wiki/K-means_clustering
1. Randomly
select K centers
2. Assign each
point to nearest
center
3. Compute new
center (mean)
for each cluster

K-means algorithm
Illustration: http://en.wikipedia.org/wiki/K-means_clustering
1. Randomly
select K centers
2. Assign each
point to nearest
center
3. Compute new
center (mean)
for each cluster
Back to 2

K-means
1. Initialize cluster centers: c0 ; t=0
2. Assign each point to the closest center
3. Update cluster centers as the mean of the points
4. Repeat 2-3 until no points are re-assigned (t=t+1)
 
 
 
N
j
K
i
j
t
i
N
t
ij
2
1
1
argmin x
c
δ
δ

 
 

N
j
K
i
j
i
t
N
t
ij
2
1
argmin x
c
c
c

Slide: Derek Hoiem

K-means converges to a local minimum

K-means: design choices
• Initialization
– Randomly select K points as initial cluster center
– Or greedily choose K points to minimize residual
• Distance measures
– Traditionally Euclidean, could be others
• Optimization
– Will converge to a local minimum
– May want to perform multiple restarts

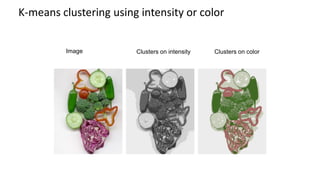
Image Clusters on intensity Clusters on color
K-means clustering using intensity or color

How to evaluate clusters?
• Generative
– How well are points reconstructed from the clusters?
• Discriminative
– How well do the clusters correspond to labels?
• Purity
– Note: unsupervised clustering does not aim to be discriminative
Slide: Derek Hoiem

How to choose the number of clusters?
• Validation set
– Try different numbers of clusters and look at performance
• When building dictionaries (discussed later), more clusters typically work
better
Slide: Derek Hoiem

K-Means pros and cons
• Pros
• Finds cluster centers that minimize
conditional variance (good
representation of data)
• Simple and fast*
• Easy to implement
• Cons
• Need to choose K
• Sensitive to outliers
• Prone to local minima
• All clusters have the same parameters
(e.g., distance measure is non-
adaptive)
• *Can be slow: each iteration is O(KNd)
for N d-dimensional points
• Usage
• Rarely used for pixel segmentation

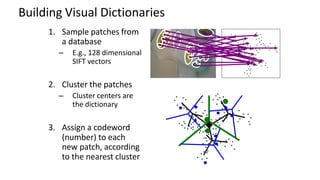
Building Visual Dictionaries
1. Sample patches from
a database
– E.g., 128 dimensional
SIFT vectors
2. Cluster the patches
– Cluster centers are
the dictionary
3. Assign a codeword
(number) to each
new patch, according
to the nearest cluster

Examples of learned codewords
Sivic et al. ICCV 2005
http://www.robots.ox.ac.uk/~vgg/publications/papers/sivic05b.pdf
Most likely codewords for 4 learned “topics”

Agglomerative clustering
How to define cluster similarity?
- Average distance between points, maximum
distance, minimum distance
- Distance between means or medoids
How many clusters?
- Clustering creates a dendrogram (a tree)
- Threshold based on max number of clusters
or based on distance between merges
distance

Conclusions: Agglomerative Clustering
Good
• Simple to implement, widespread application
• Clusters have adaptive shapes
• Provides a hierarchy of clusters
Bad
• May have imbalanced clusters
• Still have to choose number of clusters or threshold
• Need to use an “ultrametric” to get a meaningful hierarchy

• Versatile technique for clustering-based
segmentation
D. Comaniciu and P. Meer, Mean Shift: A Robust Approach toward Feature Space Analysis, PAMI 2002.
Mean shift segmentation

Mean shift algorithm
• Try to find modes of this non-parametric density

Kernel density estimation
Kernel density estimation function
Gaussian kernel

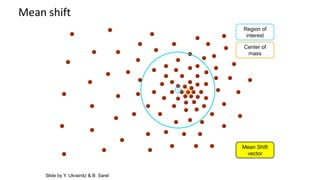
Region of
interest
Center of
mass
Mean Shift
vector
Slide by Y. Ukrainitz & B. Sarel
Mean shift

Region of
interest
Center of
mass
Mean Shift
vector
Mean shift

Region of
interest
Center of
mass
Mean shift

Simple Mean Shift procedure:
• Compute mean shift vector
•Translate the Kernel window by m(x)
2
1
2
1
( )
n
i
i
i
n
i
i
g
h
g
h


 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 


x - x
x
m x x
x - x
g( ) ( )
k
 
x x
Computing the Mean Shift

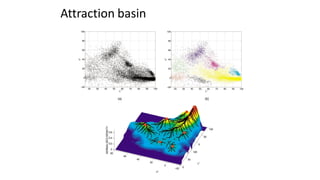
• Attraction basin: the region for which all
trajectories lead to the same mode
• Cluster: all data points in the attraction
basin of a mode
Attraction basin

Mean shift clustering
• The mean shift algorithm seeks modes of the given set of
points
1. Choose kernel and bandwidth
2. For each point:
a) Center a window on that point
b) Compute the mean of the data in the search window
c) Center the search window at the new mean location
d) Repeat (b,c) until convergence
3. Assign points that lead to nearby modes to the same cluster

• Compute features for each pixel (color, gradients, texture, etc)
• Set kernel size for features Kf and position Ks
• Initialize windows at individual pixel locations
• Perform mean shift for each window until convergence
• Merge windows that are within width of Kf and Ks
Segmentation by Mean Shift

Mean shift segmentation results
Comaniciu and Meer 2002

Mean shift pros and cons
• Pros
– Good general-practice segmentation
– Flexible in number and shape of regions
– Robust to outliers
• Cons
– Have to choose kernel size in advance
– Not suitable for high-dimensional features
• When to use it
– Oversegmentatoin
– Multiple segmentations
– Tracking, clustering, filtering applications

Which algorithm to try first?
• Quantization/Summarization: K-means
– Aims to preserve variance of original data
– Can easily assign new point to a cluster
Quantization for
computing histograms
Summary of 20,000 photos of Rome using
“greedy k-means”
http://grail.cs.washington.edu/projects/canonview/

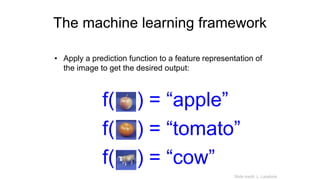
The machine learning framework
• Apply a prediction function to a feature representation of
the image to get the desired output:
f( ) = “apple”
f( ) = “tomato”
f( ) = “cow”
Slide credit: L. Lazebnik

The machine learning framework
y = f(x)
• Training: given a training set of labeled examples {(x1,y1),
…, (xN,yN)}, estimate the prediction function f by minimizing
the prediction error on the training set
• Testing: apply f to a never before seen test example x and
output the predicted value y = f(x)
output prediction
function
Image
feature

Learning a classifier
Given some set of features with corresponding labels, learn a
function to predict the labels from the features
x x
x
x
x
x
x
x
o
o
o
o
o
x2
x1

Prediction
Steps
Training
Labels
Training
Images
Training
Training
Image
Features
Image
Features
Testing
Test Image
Learned
model
Learned
model
Slide credit: D. Hoiem and L. Lazebnik

Features
• Raw pixels
• Histograms
• GIST descriptors
• … Slide credit: L. Lazebnik

One way to think about it…
• Training labels dictate that two examples are the same or
different, in some sense
• Features and distance measures define visual similarity
• Classifiers try to learn weights or parameters for features and
distance measures so that visual similarity predicts label
similarity

Many classifiers to choose from
• SVM
• Neural networks
• Naïve Bayes
• Bayesian network
• Logistic regression
• Randomized Forests
• Boosted Decision Trees
• K-nearest neighbor
• RBMs
• Deep Convolutional Network
• Etc.
Which is the best one?

Claim:
The decision to use machine learning
is more important than the choice of
a particular learning method.
*Deep learning seems to be an exception to this, at
the moment, probably because it is learning the
feature representation.

Classifiers: Nearest neighbor
f(x) = label of the training example nearest to x
• All we need is a distance function for our inputs
• No training required!
Test
example
Training
examples
from class 1
Training
examples
from class 2

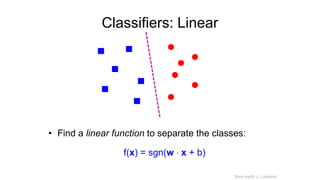
Classifiers: Linear
• Find a linear function to separate the classes:
f(x) = sgn(w  x + b)

• Images in the training set must be annotated with the
“correct answer” that the model is expected to produce
Contains a motorbike
Recognition task and supervision

Unsupervised “Weakly” supervised Fully supervised
Definition depends on task

Generalization
• How well does a learned model generalize from
the data it was trained on to a new test set?
Training set (labels known) Test set (labels
unknown)

Generalization
• Components of generalization error
– Bias: how much the average model over all training sets differ
from the true model?
• Error due to inaccurate assumptions/simplifications made by
the model. “Bias” sounds negative. “Regularization” sounds
nicer.
– Variance: how much models estimated from different training
sets differ from each other.
• Underfitting: model is too “simple” to represent all the
relevant class characteristics
– High bias (few degrees of freedom) and low variance
– High training error and high test error
• Overfitting: model is too “complex” and fits irrelevant
characteristics (noise) in the data
– Low bias (many degrees of freedom) and high variance
– Low training error and high test error

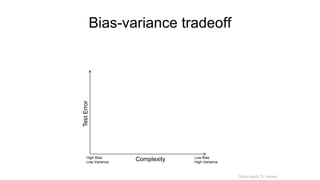
Bias-Variance Trade-off
• Models with too few
parameters are
inaccurate because of a
large bias (not enough
flexibility).
• Models with too many
parameters are
inaccurate because of a
large variance (too much
sensitivity to the sample).
Slide credit: D. Hoiem

Bias-variance tradeoff
Training error
Test error
Underfitting Overfitting
Complexity Low Bias
High Variance
High Bias
Low Variance
Error

Bias-variance tradeoff
Many training examples
Few training examples
Complexity Low Bias
High Variance
High Bias
Low Variance
Test
Error

Effect of Training Size
Testing
Training
Generalization Error
Number of Training Examples
Error
Fixed prediction model

Remember…
• No classifier is inherently
better than any other: you
need to make assumptions to
generalize
• Three kinds of error
– Inherent: unavoidable
– Bias: due to over-simplifications
– Variance: due to inability to
perfectly estimate parameters
from limited data

• How to reduce variance?
– Choose a simpler classifier
– Regularize the parameters
– Get more training data
• How to reduce bias?
– Choose a more complex, more expressive classifier
– Remove regularization
– (These might not be safe to do unless you get more training data)

Computer Vision Computer Vision: Algorithms and Applications Richard Szeliski

More Related Content

Similar to Computer Vision Computer Vision: Algorithms and Applications Richard Szeliski (20)

Recently uploaded (20)

Computer Vision Computer Vision: Algorithms and Applications Richard Szeliski