Concurrency Control in Database Management System
- 2. Problems associated with concurrency ● The lost update problem ● The uncommitted dependency problem ● The inconsistent analysis problem
- 3. concurrency ▪ The lost update problem
- 4. concurrency ▪ The uncommitted dependency problem
- 5. concurrency ▪ The inconsistent analysis problem
- 6. Concurrency control techniques ▪ Lock-based protocols ▪ Timestamp-Based Protocols ▪ Validation-Based Protocols
- 7. Lock-Based Protocols ▪ A lock is a mechanism to control concurrent access to a data item ▪ Data items can be locked in two modes : 1. exclusive (X) mode. Data item can be both read as well as written. X-lock is requested using lock-X instruction. 2. shared (S) mode. Data item can only be read. S-lock is requested using lock-S instruction. ▪ To access a data item Q, a transaction must first lock that item by executing the lock-S(Q) or lock-X(Q) instruction. ▪ Lock requests are made to concurrency-control manager. Transaction can proceed only after request is granted. ▪ A transaction can unlock a data item Q by the unlock(Q) instruction.
- 8. Lock-Based Protocols (Cont.) ▪ Example of a transaction performing locking: T2 : lock-S(A); read (A); unlock(A); lock-S(B); read (B); unlock(B); display(A+B) ▪ Locking as above is not sufficient to guarantee serializability
- 9. Lock-Based Protocols (Cont.) ▪ Lock-compatibility matrix ▪ A transaction may be granted a lock on an item if the requested lock is compatible with locks already held on the item by other transactions. Otherwise the transaction requesting a lock is made to wait until all incompatible locks held by other transactions have been released. ▪ Any number of transactions can hold shared locks on an item, ▪ But if any transaction holds an exclusive on the item no other transaction may hold any lock on the item.
- 10. Locking Protocols ▪ WR, RW and WW anomalies can be avoided using a locking protocol ▪ A locking protocol: ▪ Is a set of rules to be followed by each transaction to ensure that only serializable schedules are allowed (extended later) ▪ Associates a lock with each database object, which could be of different types (e.g., shared or exclusive) ▪ Grants and denies locks to transactions according to the specified rules ▪ The part of the DBMS that keeps track of locks is called the lock manager
- 11. Schedule With Lock Grants ▪ Grants omitted in rest of chapter • Assume grant happens just before the next instruction following lock request ▪ A locking protocol is a set of rules followed by all transactions while requesting and releasing locks. ▪ Locking protocols enforce serializability by restricting the set of possible schedules.
- 12. Locking Protocols ▪ Given a locking protocol (such as 2PL) • A schedule S is legal under a locking protocol if it can be generated by a set of transactions that follow the protocol • A protocol ensures serializability if all legal schedules under that protocol are serializable
- 13. The Two-Phase Locking Protocol (Cont.) ▪ Two-phase locking does not ensure freedom from deadlocks ▪ Extensions to basic two-phase locking needed to ensure recoverability of freedom from cascading roll-back • Strict two-phase locking: a transaction must hold all its exclusive locks till it commits/aborts. ▪ Ensures recoverability and avoids cascading roll-backs • Rigorous two-phase locking: a transaction must hold all locks till commit/abort. ▪ Transactions can be serialized in the order in which they commit. ▪ Most databases implement rigorous two-phase locking, but refer to it as simply two-phase locking
- 14. The Two-Phase Locking Protocol (Cont.) ▪ Two-phase locking is not a necessary condition for serializability • There are conflict serializable schedules that cannot be obtained if the two-phase locking protocol is used. ▪ In the absence of extra information (e.g., ordering of access to data), two-phase locking is necessary for conflict serializability in the following sense: • Given a transaction Ti that does not follow two-phase locking, we can find a transaction Tj that uses two-phase locking, and a schedule for Ti and Tj
- 15. Lock Managers ▪ Usually, a lock manager in a DBMS maintains three types of data structures: ▪ A queue, Q, for each lock, L, to hold its pending requests ▪ A lock table, which keeps for each L associated with each object, O, a record R that contains: ▪ The type of L (e.g., shared or exclusive) ▪ The number of transactions currently holding L on O ▪ A pointer to Q ▪ A transaction table, which maintains for each transaction, T, a pointer to a list of locks held by T Lock Queue 1 (Q1) Object Lock # Type # of Trx Q O L S 1 Q1 Lock Table Transaction List 1 (LS1) Trx List T1 LS1 Transaction Table
- 16. Two-Phase Locking ▪ A widely used locking protocol, called Two-Phase Locking (2PL), has two rules: ▪ Rule 1: if a transaction T wants to read (or write) an object O, it first requests the lock manager for a shared (or exclusive) lock on O T0 T1 T2 Lock Manager Read Request on Object O “Shared” Lock Granted Queue T0 T1 T2 Lock Manager Write Request on Object O Lock Denied Queue T0 T1 T2 Lock Manager Read Request on Object O “Shared” Lock Granted Queue 2 Time t0 t1 t2
- 17. Two-Phase Locking ▪ A widely used locking protocol, called Two-Phase Locking (2PL), has two rules: ▪ Rule 1: if a transaction T wants to read (or write) an object O, it first requests the lock manager for a shared (or exclusive) lock on O T0 T1 T2 Lock Manager Release Lock on Object O Queue T0 T1 T2 Lock Manager “Exclusive” Lock Granted Queue T0 T1 T2 Lock Manager Release Lock on Object O Queue 2 Time t3 t4 t5 2 2
- 18. Two-Phase Locking ▪ A widely used locking protocol, called Two-Phase Locking (2PL), has two rules: ▪ Rule 1: if a transaction T wants to read (or write) an object O, it first requests the lock manager for a shared (or exclusive) lock on O T0 T1 T2 Lock Manager Queue T0 T1 T2 Lock Manager Queue T0 T1 T2 Lock Manager Queue Time Read Request on Object O Lock Denied 1 Read Request on Object O Lock Denied 0 Release Lock on Object O t6 t7 t8 1 0 1
- 19. Two-Phase Locking ▪ A widely used locking protocol, called Two-Phase Locking (2PL), has two rules: ▪ Rule 1: if a transaction T wants to read (or write) an object O, it first requests the lock manager for a shared (or exclusive) lock on O T0 T1 T2 Lock Manager Queue T0 T1 T2 Lock Manager Queue T0 T1 T2 Lock Manager Queue Time 1 0 “Shared” Lock Granted “Shared” Lock Granted t9 t9 Write Request on Object O Lock Denied 2 t10 0
- 20. Two-Phase Locking ▪ A widely used locking protocol, called Two-Phase Locking (2PL), has two rules: ▪ Rule 2: T can release locks before it commits or aborts, and cannot request additional locks once it releases any lock ▪ Thus, every transaction has a “growing” phase in which it acquires locks, followed by a “shrinking” phase in which it releases locks # locks growing phase shrinking phase
- 21. Two-Phase Locking ▪ A widely used locking protocol, called Two-Phase Locking (2PL), has two rules: ▪ Rule 2: T can release locks before it commits or aborts, and cannot request additional locks once it releases any lock ▪ Thus, every transaction has a “growing” phase in which it acquires locks, followed by a “shrinking” phase in which it releases locks # locks violation of 2PL
- 22. Automatic Acquisition of Locks ▪ A transaction Ti issues the standard read/write instruction, without explicit locking calls. ▪ The operation read(D) is processed as: if Ti has a lock on D then read(D) else begin if necessary wait until no other transaction has a lock-X on D grant Ti a lock-S on D; read(D) end
- 23. Automatic Acquisition of Locks (Cont.) ▪ write(D) is processed as: if Ti has a lock-X on D then write(D) else begin if necessary wait until no other trans. has any lock on D, if Ti has a lock-S on D then upgrade lock on D to lock-X else grant Ti a lock-X on D write(D) end; ▪ All locks are released after commit or abort
- 24. Exercise Consider the following two transactions: T34: read(A); read(B); if A = 0 then B:=B+1; write(B). T35: read(B); read(A); if B = 0 then A:=A+1; write(A). Add lock and unlock instructions to transactions T31 and T32, so that they observe the two-phase locking protocol.
- 25. Resolving RW Conflicts Using 2PL ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 reads A ▪ T2 reads A, decrements A and commits ▪ T1 tries to decrement A ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) Commit R(A) W(A) Commit Exposes RW Anomaly T1 T2 EXCLUSIVE(A) R(A) W(A) Commit EXCLUSIVE(A) R(A) W(A) Commit Lock(A) Wait RW Conflict Resolved!
- 26. Resolving RW Conflicts Using 2PL ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 reads A ▪ T2 reads A, decrements A and commits ▪ T1 tries to decrement A ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) Commit R(A) W(A) Commit Exposes RW Anomaly T1 T2 EXCLUSIVE(A) R(A) W(A) Commit Lock(A) Wait But, it can limit parallelism! EXCLUSIVE(A) R(A) W(A) Commit
- 27. Resolving WW Conflicts Using 2PL ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 sets Mohammad’s Salary to $1000 ▪ T2 sets Ahmad’s Salary to $2000 ▪ T1 sets Ahmad’s Salary to $1000 ▪ T2 sets Mohammad’s Salary to $2000 ▪ T1 and T2 can be represented by the following schedule: T1 T2 W(MS) W(AS) Commit W(AS) W(MS) Commit Exposes WW Anomaly (assuming, MS & AS must be kept equal) T1 T2 EXCLUSIVE(MS) EXCLUSIVE(AS) W(MS) W(AS) Commit EXCLUSIVE(AS) EXCLUSIVE(MS) W(AS) W(MS) Commit Lock(AS) Wait WW Conflict Resolved!
- 28. Resolving WW Conflicts Using 2PL ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 sets Mohammad’s Salary to $1000 ▪ T2 sets Ahmad’s Salary to $2000 ▪ T1 sets Ahmad’s Salary to $1000 ▪ T2 sets Mohammad’s Salary to $2000 ▪ T1 and T2 can be represented by the following schedule: T1 T2 W(MS) W(AS) Commit W(AS) W(MS) Commit Exposes WW Anomaly (assuming, MS & AS must be kept equal) T1 T2 EXCLUSIVE(MS) W(MS) Lock(AS) EXCLUSIVE(AS) W(AS) Lock(MS) Wait Deadlock! Wait
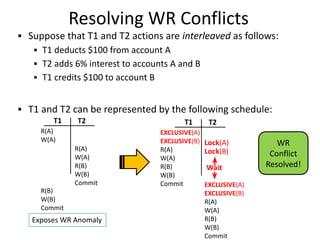
- 29. Resolving WR Conflicts ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 deducts $100 from account A ▪ T2 adds 6% interest to accounts A and B ▪ T1 credits $100 to account B ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) R(B) W(B) Commit R(A) W(A) R(B) W(B) Commit Exposes WR Anomaly T1 T2 EXCLUSIVE(A) EXCLUSIVE(B) R(A) W(A) R(B) W(B) Commit EXCLUSIVE(A) EXCLUSIVE(B) R(A) W(A) R(B) W(B) Commit Lock(A) Wait Lock(B) WR Conflict Resolved!
- 30. Resolving WR Conflicts ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 deducts $100 from account A ▪ T2 adds 6% interest to accounts A and B ▪ T1 credits $100 to account B ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) R(B) W(B) Commit R(A) W(A) R(B) W(B) Commit Exposes WR Anomaly T1 T2 EXCLUSIVE(A) EXCLUSIVE(B) R(A) W(A) RELEASE(A) R(B) W(B) Commit EXCLUSIVE(A) R(A) W(A) EXCLUSIVE(B) R(B) W(B) Commit Lock(A) Wait Lock(B) WR Conflict is NOT Resolved! How can we solve this?
- 31. Strict Two-Phase Locking ▪ WR conflicts (as well as RW & WW) can be solved by making 2PL stricter ▪ In particular, Rule 2 in 2PL can be modified as follows: ▪ Rule 2: locks of a transaction T can only be released after T completes (i.e., commits or aborts) ▪ This version of 2PL is called Strict Two-Phase Locking
- 32. Resolving WR Conflicts: Revisit ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 deducts $100 from account A ▪ T2 adds 6% interest to accounts A and B ▪ T1 credits $100 to account B ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) R(B) W(B) Commit R(A) W(A) R(B) W(B) Commit Exposes WR Anomaly T1 T2 EXCLUSIVE(A) EXCLUSIVE(B) R(A) W(A) RELEASE(A) R(B) W(B) Commit EXCLUSIVE(A) R(A) W(A) EXCLUSIVE(B) R(B) W(B) Commit Lock(A) Wait Lock(B) Not allowed with strict 2PL
- 33. Resolving WR Conflicts: Revisit ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 deducts $100 from account A ▪ T2 adds 6% interest to accounts A and B ▪ T1 credits $100 to account B ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) R(B) W(B) Commit R(A) W(A) R(B) W(B) Commit Exposes WR Anomaly T1 T2 EXCLUSIVE(A) EXCLUSIVE(B) R(A) W(A) R(B) W(B) Commit EXCLUSIVE(A) EXCLUSIVE(B) R(A) W(A) R(B) W(B) Commit Lock(A) Wait Lock(B) WR Conflict is Resolved! But, parallelism is limited more!
- 34. 2PL vs. Strict 2PL ▪ Two-Phase Locking (2PL): ▪ Limits concurrency ▪ May lead to deadlocks ▪ May have ‘dirty reads’ ▪ Strict 2PL: ▪ Limits concurrency more (but, actions of different transactions can still be interleaved) ▪ May still lead to deadlocks ▪ Avoids ‘dirty reads’ T1 T2 SHARED(A) R(A) EXCLUSIVE(C) R(C) W(C) Commit SHARED(A) R(A) EXECLUSIVE(B) R(B) W(B) Commit A Schedule with Strict 2PL and Interleaved Actions
- 35. Implementation of Locking ▪ A lock manager can be implemented as a separate process ▪ Transactions can send lock and unlock requests as messages ▪ The lock manager replies to a lock request by sending a lock grant messages (or a message asking the transaction to roll back, in case of a deadlock) • The requesting transaction waits until its request is answered ▪ The lock manager maintains an in-memory data-structure called a lock table to record granted locks and pending requests
- 36. Lock Table ▪ Dark rectangles indicate granted locks, light colored ones indicate waiting requests ▪ Lock table also records the type of lock granted or requested ▪ New request is added to the end of the queue of requests for the data item, and granted if it is compatible with all earlier locks ▪ Unlock requests result in the request being deleted, and later requests are checked to see if they can now be granted ▪ If transaction aborts, all waiting or granted requests of the transaction are deleted • lock manager may keep a list of locks held by each transaction, to implement this efficiently
- 37. Graph-Based Protocols ▪ Graph-based protocols are an alternative to two-phase locking ▪ Impose a partial ordering → on the set D = {d1 , d2 ,..., dh } of all data items. • If di → dj then any transaction accessing both di and dj must access di before accessing dj . • Implies that the set D may now be viewed as a directed acyclic graph, called a database graph. ▪ The tree-protocol is a simple kind of graph protocol.
- 38. Tree Protocol Tree protocol: 1. Only exclusive locks are allowed. 2. The first lock by Ti may be on any data item. Subsequently, a data Q can be locked by Ti only if the parent of Q is currently locked by Ti . 3. Data items may be unlocked at any time. 4. A data item that has been locked and unlocked by Ti cannot subsequently be relocked by Ti
- 39. Graph-Based Protocols (Cont.) ▪ The tree protocol ensures conflict serializability as well as freedom from deadlock. ▪ Unlocking may occur earlier in the tree-locking protocol than in the two-phase locking protocol. • Shorter waiting times, and increase in concurrency • Protocol is deadlock-free, no rollbacks are required ▪ Drawbacks • Protocol does not guarantee recoverability or cascade freedom ▪ Need to introduce commit dependencies to ensure recoverability • Transactions may have to lock data items that they do not access. ▪ increased locking overhead, and additional waiting time ▪ potential decrease in concurrency ▪ Schedules not possible under two-phase locking are possible under the tree protocol, and vice versa.
- 40. Performance of Locking ▪ Locking comes with delays mainly from blocking ▪ Usually, the first few transactions are unlikely to conflict ▪ Throughput can rise in proportion to the number of active transactions ▪ As more transactions are executed concurrently, the likelihood of blocking increases ▪ Throughput will increase more slowly with the number of active transactions ▪ There comes a point when adding another active transaction will actually decrease throughput ▪ When the system thrashes!
- 41. Performance of Locking (Cont’d) ▪ If a database begins to thrash, the DBA should reduce the number of active transactions ▪ Empirically, thrashing is seen to occur when 30% of active transactions are blocked! # of Active Transactions Throughput Thrashing
- 42. Schedules with Aborted Transactions ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 deducts $100 from account A ▪ T2 adds 6% interest to accounts A and B, and commits ▪ T1 is aborted ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) Abort R(A) W(A) R(B) W(B) Commit T2 read a value for A that should have never been there! How can we deal with the situation, assuming T2 had not yet committed?
- 43. Schedules with Aborted Transactions ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 deducts $100 from account A ▪ T2 adds 6% interest to accounts A and B, and commits ▪ T1 is aborted ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) Abort R(A) W(A) R(B) W(B) Commit We can cascade the abort of T1 by aborting T2 as well! This “cascading process” can be recursively applied to any transaction that read A written by T1 T2 read a value for A that should have never been there!
- 44. Schedules with Aborted Transactions ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 deducts $100 from account A ▪ T2 adds 6% interest to accounts A and B, and commits ▪ T1 is aborted ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) Abort R(A) W(A) R(B) W(B) Commit How can we deal with the situation, assuming T2 had actually committed? The schedule is indeed unrecoverable! T2 read a value for A that should have never been there!
- 45. Schedules with Aborted Transactions ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 deducts $100 from account A ▪ T2 adds 6% interest to accounts A and B, and commits ▪ T1 is aborted ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) Abort R(A) W(A) R(B) W(B) Commit For a schedule to be recoverable, transactions should commit only after all transactions whose changes they read commit! “Recoverable schedules” avoid cascading aborts! T2 read a value for A that should have never been there!
- 46. Schedules with Aborted Transactions ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 deducts $100 from account A ▪ T2 adds 6% interest to accounts A and B, and commits ▪ T1 is aborted ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) Abort R(A) W(A) R(B) W(B) Commit How can we ensure “recoverable schedules”? By using Strict 2PL! T2 read a value for A that should have never been there!
- 47. Schedules with Aborted Transactions ▪ Suppose that T1 and T2 actions are interleaved as follows: ▪ T1 deducts $100 from account A ▪ T2 adds 6% interest to accounts A and B, and commits ▪ T1 is aborted ▪ T1 and T2 can be represented by the following schedule: T1 T2 R(A) W(A) Abort R(A) W(A) R(B) W(B) Commit T1 T2 EXCLUSIVE(A) R(A) W(A) Abort UNDO(T1) EXCLUSIVE(A) R(A) W(A) EXCLUSIVE(B) R(B) W(B) Commit Lock(A) Wait Cascaded aborts are avoided!
- 48. Serializable Schedules: Redefined ▪ Two schedules are said to be equivalent if for any database state, the effect of executing the 1st schedule is identical to the effect of executing the 2nd schedule ▪ Previously: a serializable schedule is a schedule that is equivalent to a serial schedule ▪ Now: a serializable schedule is a schedule that is equivalent to a serial schedule over a set of committed transactions ▪ This definition captures serializability as well as recoverability
- 49. Deadlock ▪ Consider the partial schedule ▪ Neither T3 nor T4 can make progress — executing lock-S(B) causes T4 to wait for T3 to release its lock on B, while executing lock-X(A) causes T3 to wait for T4 to release its lock on A. ▪ Such a situation is called a deadlock. • To handle a deadlock one of T3 or T4 must be rolled back and its locks released.
- 50. Deadlock (Cont.) ▪ The potential for deadlock exists in most locking protocols. Deadlocks are a necessary evil (deadlocks are preferable to inconsistent states). ▪ Starvation is also possible if concurrency control manager is badly designed. For example: • A transaction may be waiting for an X-lock on an item, while a sequence of other transactions request and are granted an S-lock on the same item. • The same transaction is repeatedly rolled back due to deadlocks. ▪ Concurrency control manager can be designed to prevent starvation.
- 51. Deadlock Handling ▪ System is deadlocked if there is a set of transactions such that every transaction in the set is waiting for another transaction in the set.
- 52. Deadlock Detection ▪ Wait-for graph • Vertices: transactions • Edge from Ti →Tj . : if Ti is waiting for a lock held in conflicting mode byTj ▪ The system is in a deadlock state if and only if the wait-for graph has a cycle. ▪ Invoke a deadlock-detection algorithm periodically to look for cycles. Wait-for graph without a cycle Wait-for graph with a cycle
- 53. Exercise Consider the following sequence of events in a schedule involving transactions T1, T2, T3, T4 and T5. A, B, C, D, E, F are items in the database. Draw a wait-for-graph for the data above and find whether the transactions are in a deadlock or not?
- 54. Lock Conversions ▪ A transaction may need to change the lock it already acquires on an object ▪ From Shared to Exclusive ▪ This is referred to as lock upgrade ▪ From Exclusive to Shared ▪ This is referred to as lock downgrade ▪ For example, an SQL update statement might acquire a Shared lock on each row, R, in a table and if R satisfies the condition (in the WHERE clause), an Exclusive lock must be obtained for R
- 55. Lock Upgrades ▪ A lock upgrade request from a transaction T on object O must be handled specially by: ▪ Granting an Exclusive lock to T immediately if no other transaction holds a lock on O ▪ Otherwise, queuing T at the front of O’s queue (i.e., T is favored) ▪ T is favored because it already holds a Shared lock on O ▪ Queuing T in front of another transaction T’ that holds no lock on O, but requested an Exclusive lock on O averts a deadlock! ▪ However, if T and T’ hold a Shared lock on O, and both request upgrades to an Exclusive lock, a deadlock will arise regardless!
- 56. Lock Downgrades ▪ Lock upgrades can be entirely avoided by obtaining Exclusive locks initially, and downgrade them to Shared locks once needed ▪ Would this violate any 2PL requirement? ▪ On the surface yes; since the transaction (say, T) may need to upgrade later ▪ This is a special case as T conservatively obtained an Exclusive lock, and did nothing but read the object that it downgraded ▪ 2PL can be safely extended to allow lock downgrades in the growing phase, provided that the transaction has not modified the object
- 57. Deadlock Detection ▪ The lock manager maintains a structure called a waits-for graph to periodically detect deadlocks ▪ In a waits-for graph: ▪ The nodes correspond to active transactions ▪ There is an edge from Ti to Tj if and only if Ti is waiting for Tj to release a lock ▪ The lock manager adds and removes edges to and from a waits-for graph when it queues and grants lock requests, respectively ▪ A deadlock is detected when a cycle in the waits-for graph is found
- 58. Deadlock Detection (Cont’d) ▪ The following schedule is free of deadlocks: T1 T2 S(A) R(A) S(B) X(B) W(B) X(C) S(C) R(C) X(B) T3 T4 T1 T2 T4 T3 *The nodes correspond to active transactions and there is an edge from Ti to Tj if and only if Ti is waiting for Tj to release a lock The Corresponding Waits-For Graph* A schedule without a deadlock No cycles; hence, no deadlocks!
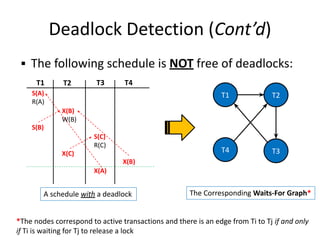
- 59. Deadlock Detection (Cont’d) ▪ The following schedule is NOT free of deadlocks: T1 T2 S(A) R(A) S(B) X(B) W(B) X(C) S(C) R(C) X(A) X(B) T3 T4 T1 T2 T4 T3 *The nodes correspond to active transactions and there is an edge from Ti to Tj if and only if Ti is waiting for Tj to release a lock The Corresponding Waits-For Graph* A schedule with a deadlock
- 60. Deadlock Detection (Cont’d) ▪ The following schedule is NOT free of deadlocks: T1 T2 S(A) R(A) S(B) X(B) W(B) X(C) S(C) R(C) X(A) X(B) T3 T4 T1 T2 T4 T3 *The nodes correspond to active transactions and there is an edge from Ti to Tj if and only if Ti is waiting for Tj to release a lock The Corresponding Waits-For Graph* A schedule with a deadlock Cycle detected; hence, a deadlock!
- 61. Resolving Deadlocks ▪ A deadlock is resolved by aborting a transaction that is on a cycle and releasing its locks ▪ This allows some of the waiting transactions to proceed ▪ The choice of which transaction to abort can be made using different criteria: ▪ The one with the fewest locks ▪ Or the one that has done the least work ▪ Or the one that is farthest from completion (more accurate) ▪ Caveat: a transaction that was aborted in the past, should be favored subsequently and not aborted upon a deadlock detection!
- 62. Deadlock Prevention ▪ Studies indicate that deadlocks are relatively infrequent and detection-based schemes work well in practice ▪ However, if there is a high level of contention for locks, prevention-based schemes could perform better ▪ Deadlocks can be averted by giving each transaction a priority and ensuring that lower-priority transactions are not allowed to wait for higher-priority ones (or vice versa)
- 63. Deadlock Handling ▪ Deadlock prevention protocols ensure that the system will never enter into a deadlock state. Some prevention strategies: • Require that each transaction locks all its data items before it begins execution (pre-declaration). • Impose partial ordering of all data items and require that a transaction can lock data items only in the order specified by the partial order (graph-based protocol).
- 64. Strategies ▪ wait-die scheme — non-preemptive • Older transaction may wait for younger one to release data item. • Younger transactions never wait for older ones; they are rolled back instead. • A transaction may die several times before acquiring a lock ▪ wound-wait scheme — preemptive • Older transaction wounds (forces rollback) of younger transaction instead of waiting for it. • Younger transactions may wait for older ones. • Fewer rollbacks than wait-die scheme. ▪ In both schemes, a rolled back transactions is restarted with its original timestamp. • Ensures that older transactions have precedence over newer ones, and starvation is thus avoided.
- 65. Deadlock prevention (Cont.) ▪ Timeout-Based Schemes: • A transaction waits for a lock only for a specified amount of time. After that, the wait times out and the transaction is rolled back. • Ensures that deadlocks get resolved by timeout if they occur • Simple to implement • But may roll back transaction unnecessarily in absence of deadlock ▪ difficult to determine good value of the timeout interval. • Starvation is also possible
- 66. Deadlock Detection ▪ Wait-for graph • Vertices: transactions • Edge from Ti →Tj . : if Ti is waiting for a lock held in conflicting mode byTj ▪ The system is in a deadlock state if and only if the wait-for graph has a cycle. ▪ Invoke a deadlock-detection algorithm periodically to look for cycles. Wait-for graph without a cycle Wait-for graph with a cycle
- 67. Deadlock Recovery ▪ When deadlock is detected : • Some transaction will have to be rolled back (made a victim) to break deadlock cycle. ▪ Select that transaction as victim that will incur minimum cost • Rollback -- determine how far to roll back transaction ▪ Total rollback: Abort the transaction and then restart it. ▪ Partial rollback: Roll back victim transaction only as far as necessary to release locks that another transaction in cycle is waiting for ▪ Starvation can happen (why?) • One solution: oldest transaction in the deadlock set is never chosen as victim
- 68. Multiple Granularity ▪ Allow data items to be of various sizes and define a hierarchy of data granularities, where the small granularities are nested within larger ones ▪ Can be represented graphically as a tree (but don't confuse with tree-locking protocol) ▪ When a transaction locks a node in the tree explicitly, it implicitly locks all the node's descendents in the same mode. ▪ Granularity of locking (level in tree where locking is done): • Fine granularity (lower in tree): high concurrency, high locking overhead • Coarse granularity (higher in tree): low locking overhead, low concurrency
- 69. Example of Granularity Hierarchy The levels, starting from the coarsest (top) level are • database • area • file • record
- 70. Intention Lock Modes ▪ In addition to S and X lock modes, there are three additional lock modes with multiple granularity: • intention-shared (IS): indicates explicit locking at a lower level of the tree but only with shared locks. • intention-exclusive (IX): indicates explicit locking at a lower level with exclusive or shared locks • shared and intention-exclusive (SIX): the subtree rooted by that node is locked explicitly in shared mode and explicit locking is being done at a lower level with exclusive-mode locks. ▪ intention locks allow a higher level node to be locked in S or X mode without having to check all descendent nodes.
- 71. Compatibility Matrix with Intention Lock Modes ▪ The compatibility matrix for all lock modes is:
- 72. Multiple Granularity Locking Scheme ▪ Transaction Ti can lock a node Q, using the following rules: 1. The lock compatibility matrix must be observed. 2. The root of the tree must be locked first, and may be locked in any mode. 3. A node Q can be locked by Ti in S or IS mode only if the parent of Q is currently locked by Ti in either IX or IS mode. 4. A node Q can be locked by Ti in X, SIX, or IX mode only if the parent of Q is currently locked by Ti in either IX or SIX mode. 5. Ti can lock a node only if it has not previously unlocked any node (that is, Ti is two-phase). 6. Ti can unlock a node Q only if none of the children
- 73. Deadlock Handling ▪ Deadlock prevention protocols ensure that the system will never enter into a deadlock state. Some prevention strategies: • Require that each transaction locks all its data items before it begins execution (pre-declaration). • Impose partial ordering of all data items and require that a transaction can lock data items only in the order specified by the partial order (graph-based protocol).
- 74. More Deadlock Prevention Strategies ▪ wait-die scheme — non-preemptive • Older transaction may wait for younger one to release data item. • Younger transactions never wait for older ones; they are rolled back instead. • A transaction may die several times before acquiring a lock ▪ wound-wait scheme — preemptive • Older transaction wounds (forces rollback) of younger transaction instead of waiting for it. • Younger transactions may wait for older ones. • Fewer rollbacks than wait-die scheme. ▪ In both schemes, a rolled back transactions is restarted with its original timestamp. • Ensures that older transactions have precedence over newer ones, and starvation is thus avoided.
- 75. Deadlock prevention (Cont.) ▪ Timeout-Based Schemes: • A transaction waits for a lock only for a specified amount of time. After that, the wait times out and the transaction is rolled back. • Ensures that deadlocks get resolved by timeout if they occur • Simple to implement • But may roll back transaction unnecessarily in absence of deadlock ▪ difficult to determine good value of the timeout interval. • Starvation is also possible
- 76. Deadlock Prevention (Cont’d) ▪ One way to assign priorities is to give each transaction a timestamp when it is started ▪ Thus, the lower the timestamp, the higher is the transaction’s priority ▪ If a transaction Ti requests a lock and a transaction Tj holds a conflicting lock, the lock manager can use one of the following policies: ▪ Wound-Wait: If Ti has higher priority, Tj is aborted; otherwise, Ti waits ▪ Wait-Die: If Ti has higher priority, it is allowed to wait; otherwise, it is aborted
- 77. Timestamp-Based Protocols ▪ Each transaction Ti is issued a timestamp TS(Ti ) when it enters the system. • Each transaction has a unique timestamp • Newer transactions have timestamps strictly greater than earlier ones • Two simple methods for implementing this scheme: ▪ Use the value of the system clock as the timestamp ▪ Use a logical counter that is incremented after a new timestamp has been assigned ▪ Timestamp-based protocols manage concurrent execution such that time-stamp order = serializability order i.e., if TS(Ti ) < TS(Tj ), the produced schedule is equivalent to a serial schedule in which Ti appears before Tj. ▪ Several alternative protocols based on timestamps
- 78. Timestamp-Ordering Protocol The timestamp ordering (TSO) protocol ▪ Maintains for each data Q two timestamp values: • W-timestamp(Q) is the largest time-stamp of any transaction that executed write(Q) successfully. • R-timestamp(Q) is the largest time-stamp of any transaction that executed read(Q) successfully. ▪ These timestamps are updated whenever a new read(Q) or write(Q) instruction is executed. ▪ Imposes rules on read and write operations to ensure that • any conflicting operations are executed in timestamp order • out of order operations cause transaction rollback
- 79. Timestamp-Based Protocols (Cont.) ▪ Suppose a transaction Ti issues a read(Q) 1. If TS(Ti ) ≤ W-timestamp(Q), then Ti needs to read a value of Q that was already overwritten. ▪ Hence, the read operation is rejected, and Ti is rolled back. 2. If TS(Ti ) ≥ W-timestamp(Q), then the read operation is executed, and R-timestamp(Q) is set to max(R-timestamp(Q), TS(Ti )).
- 80. Timestamp-Based Protocols (Cont.) ▪ Suppose that transaction Ti issues write(Q). 1. If TS(Ti ) < R-timestamp(Q), then the value of Q that Ti is producing was needed previously, and the system assumed that that value would never be produced. Hence, the write operation is rejected, and Ti is rolled back. 2. If TS(Ti ) < W-timestamp(Q), then Ti is attempting to write an obsolete value of Q. Hence, this write operation is rejected, and Ti is rolled back. 3. Otherwise, the write operation is executed, and W-timestamp(Q) is set to TS(Ti ).
- 81. Example of Schedule Under TSO ▪ And how about this one, where initially R-TS(Q)=W-TS(Q)=0 Assume that initially: R-TS(A) = W-TS(A) = 0 R-TS(B) = W-TS(B) = 0 Assume TS(T25 ) = 25 and TS(T26 ) = 26 ▪ Is this schedule valid under TSO?
- 82. Another Example Under TSO A partial schedule for several data items for transactions with timestamps 1, 2, 3, 4, 5, with all R-TS and W-TS = 0 initially
- 83. Correctness of Timestamp-Ordering Protocol ▪ The timestamp-ordering protocol guarantees serializability since all the arcs in the precedence graph are of the form: Thus, there will be no cycles in the precedence graph ▪ Timestamp protocol ensures freedom from deadlock as no transaction ever waits. ▪ But the schedule may not be cascade-free, and may not even be recoverable.
- 84. Recoverability and Cascade Freedom ▪ Solution 1: • A transaction is structured such that its writes are all performed at the end of its processing • All writes of a transaction form an atomic action; no transaction may execute while a transaction is being written • A transaction that aborts is restarted with a new timestamp ▪ Solution 2: Limited form of locking: wait for data to be committed before reading it ▪ Solution 3: Use commit dependencies to ensure recoverability
- 85. Thomas’ Write Rule ▪ Modified version of the timestamp-ordering protocol in which obsolete write operations may be ignored under certain circumstances. ▪ When Ti attempts to write data item Q, if TS(Ti ) < W-timestamp(Q), then Ti is attempting to write an obsolete value of {Q}. • Rather than rolling back Ti as the timestamp ordering protocol would have done, this {write} operation can be ignored. ▪ Otherwise this protocol is the same as the timestamp ordering protocol. ▪ Thomas' Write Rule allows greater potential concurrency. • Allows some view-serializable schedules that are not conflict-serializable.
- 86. Validation-Based Protocol ▪ Idea: can we use commit time as serialization order? ▪ To do so: • Postpone writes to end of transaction • Keep track of data items read/written by transaction • Validation performed at commit time, detect any out-of-serialization order reads/writes ▪ Also called as optimistic concurrency control since transaction executes fully in the hope that all will go well during validation
- 87. Validation-Based Protocol ▪ Execution of transaction Ti is done in three phases. 1. Read and execution phase: Transaction Ti writes only to temporary local variables 2. Validation phase: Transaction Ti performs a '‘validation test'' to determine if local variables can be written without violating serializability. 3. Write phase: If Ti is validated, the updates are applied to the database; otherwise, Ti is rolled back. ▪ The three phases of concurrently executing transactions can be interleaved, but each transaction must go through the three phases in that order. • We assume for simplicity that the validation and write phase occur together, atomically and serially ▪ I.e., only one transaction executes validation/write at a time.
- 88. Validation-Based Protocol (Cont.) ▪ Each transaction Ti has 3 timestamps • StartTS(Ti ) : the time when Ti started its execution • ValidationTS(Ti ): the time when Ti entered its validation phase • FinishTS(Ti ) : the time when Ti finished its write phase ▪ Validation tests use above timestamps and read/write sets to ensure that serializability order is determined by validation time • Thus, TS(Ti ) = ValidationTS(Ti ) ▪ Validation-based protocol has been found to give greater degree of concurrency than locking/TSO if probability of conflicts is low.
- 89. Validation Test for Transaction Tj ▪ If for all Ti with TS (Ti ) < TS (Tj ) either one of the following condition holds: • finishTS(Ti ) < startTS(Tj ) • startTS(Tj ) < finishTS(Ti ) < validationTS(Tj ) and the set of data items written by Ti does not intersect with the set of data items read by Tj . then validation succeeds and Tj can be committed. ▪ Otherwise, validation fails and Tj is aborted. ▪ Justification: • First condition applies when execution is not concurrent ▪ The writes of Tj do not affect reads of Ti since they occur after Ti has finished its reads. • If the second condition holds, execution is
- 90. Schedule Produced by Validation ▪ Example of schedule produced using validation