ConstructiveControlRobotsAbridged
- 1. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Constructive Approaches for Design of Networked Control Systems November 18th 2015 Dr. Nicholas Kottenstette PhD Principal Robotic Control Systems Engineer Corindus Vascular Robotics [email protected] [email protected] https://www.linkedin.com/in/nicholas-kottenstette-phd-b1b6aa14
- 2. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control OVERVIEW • Multirate Networked Control Framework for Robotic Systems – Interior Conic Systems – Properties & Feedback Control Laws – Wireless Networked Control Architecture for Conic Systems – Application I: Networked Control of a Robotic System – Application II: Telemanipulation of Haptic Paddles – Application III: Networked Coordination of Robotic Arms
- 3. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Continuous Time (CT) Interior Conic Systems 0 0 0 ( ) ( ) ( ( ) ( ) ( ) () ) 0 T T T T T T p p p p p py t y t dt a b y t u t dt ab u t u t dt 2 2 2 2) ,|| ( ) || ( || ( ) || 0T p p p p p p T T p py a b uy bu a 2 passive systems are inside the sector [0, ], strictly input passive systems are inside the sector [ , , strictly output passive systems are in ] 0 ] -stable systems are in side the sect sid or [0, e thm a b L b a e sector [a,b] , .a b Interior conic systems are inside the sector 0 [ , ] b a b a
- 4. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Discrete Time (DT) Interior Conic Systems 1 0 1 1 0 0 ( ) ( ) ( ( ) ( ) ( ) () ) 0 N N T T T p p p p p p i N ii y i y i a b y i u i ab u i u i 2 2 2 2) ,|| ( ) || ( || ( ) || 0N p p p p p p N N p py a b uy bu a 2 passive systems are inside the sector [0, ], strictly input passive systems are inside the sector [ , , strictly output passive systems are in ] 0 ] -stable systems are in side the sect sid or [0, e thm a b l b a e sector [a,b] , .a b Interior conic systems are inside the sector 0 [ , ] b a b a
- 5. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Properties: Interior Conic Systems – Sum Rule 1 1 1:H u y 1u 2 2 2:H u y 1y 2u u 1 2y y y 2y 1 1inside [ , ]a b 2 2inside [ , ]a b 1 2 1 2: inside the sector ,H u y a a b b
- 6. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Properties: Interior Conic Systems – Scaling Rule :H ku y inside [ , ]a b ku y : inside the sector , , if 0 : inside the sector , , if 0 H u y ka kb k H u y kb ka k
- 7. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Properties: Interior Conic Systems – Concatenation Rule : inside the sector , in which 1,..., max , min max 1 max max 4min . 2 2 l l l l l l l l l l l l l l l l H u y a b l m a bab a b a b a b a b a b a b a a b a b a b 1 m u u u 1 m y y y
- 8. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Properties: Interior Conic Systems – Rotation Rule T T If the matrix is an orthogonal matrix ( ) then : is inside the sector , iff : is inside the sector , .R R R R I H R u y a b H u Ry a b
- 9. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Sufficient Condition for Feedback Stability of Interior Conic Systems Dkd D D D cl If : is inside the sector [ , ] ([0, ]), , 0 and the feedback law is ( ) ( ( ) ( )) in which the gain satisfies: 1 1 when 0; 1 when 0 then : is stable. d d H a b a b b t k t t k a b a k a H b ‘D-Term’
- 10. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Feedback Stability Result for Cascades of Interior Conic Systems The following control structure, typically exploited in robotic control applications is stable under the following set of conditions. d cl : dH Pkd cl cl cl P P P If : is inside the sector [0, ] ([0,1]), 0 and : is inside the sector [0, ] ([0, ]), 0 and the feedback law is ( ) ( ( ) ( )) in which the gain satisfies 0 ,then the syst d d d H b b H b b t k t t k k em is stable. ‘P-Term’
- 11. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Inner Product Equivalent Sample and Hold (IPESH) Transform 2 2 1 ( ) p p s H sz H z T z s ( ) is inside the sector , iff ( ) is inside the sector , . p p H s a b H z a b z-1 sT 2 z-transform of sampled time series of ( )pH s s
- 12. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Further Reading • Kottenstette, N., LeBlanc, H., Eyisi, E., Koutsoukos, X. “Multi-rate networked control of conic (dissipative) systems,” 2011 ACC pp. 274-280 (TR: ISIS-09-108). • Kottenstette, N., McCourt, M.J., Xia, M., Gupta, V., Antsaklis, P.J., “On relationships among passivity, positive realness, and dissipativity in linear systems”, Automatica 50 (4), pp. 1003-1016. • Kottenstette, N., Antsaklis, P.J., "Relationships between positive real, passive dissipative, & positive systems," 2010 ACC, pp.409- 416. • Kottenstette, N., Porter, J., “Digital passive attitude and altitude control schemes for quadrotor aircraft,” 2009 ICCA, pp.1761-1768 (TR: ISIS-08-911). • G. Zames, “On the input-output stability of time-varying nonlinear feedback systems. i. conditions derived using concepts of loop gain, conicity and positivity,” TAC, vol. AC-11, no. 2, pp. 228 – 238, 1966. • J. C. Willems, The Analysis of Feedback Systems. Cambridge, MA, USA: MIT Press, 1971.
- 13. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Wireless Networked Control Architecture for Conic Systems • Render robotic system dynamics (Hp) To remain inside the sector [a,b]. • Architecture allows for accommodation of time varying channel capacity (due to communication faults/uncertainty) • If a >=0 and b is finite, then use discrete time lag compensator (Hc) to control 𝑦𝑝(t).
- 14. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Wave Variables – Plant Interface • Wave variables allow for a continuous time system to be interconnected to a discrete time controller while allowing for time varying communication delays. pe dc p pdc The wave variable transformation relates the continuous time plant "outputs" , to the corresponding "inputs" , as follows: 2 2 p p pp u t y t v t y t v tu t I I y ty t I I
- 15. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Multirate Passive Hold (PH:MTs) allows for adjustment to time varying channel capacity 1 , ,..., 1 1 1 , , 1 p c p p s s s v i v j i Mj M j M v t v i t iT i T T 2 2 s p c NMNT v v 1 1 11 12 2 22 2 1 0 1 0 1 1s l l s s i T M jm MN m N p p p c c NMNT MN l i l j i MjsiT v v i dt v v j v T M
- 16. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Multirate Passive Sampler (PS:MTs) allows for adjustment to time varying channel capacity • Filters can be classic Butterworth antialiasing filters which allows for improved noise rejection and performance. LPc LP pLP 1 1 1 if 1 if , 1, otherwise1, otherwise 1 ( ) j s jM c i j M MTH j H e M u j u i M 22 s c pN MNT u u
- 17. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Multirate Passive Sampler (PS:MTs): Proof 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 2 12 pLP 0 1 1 Use Cauchy–Schwarz Inequality (CSI): , From CSI we have: ( )1 ( ) 1 ( ) 1 ( )l jM jM jM jM i j M i j M i j M i j M jMN c N j i j M y u y u y i y i M y i u u i M 1 2 2 2 pLP 1 1 0 1 1 2 1 1 22 2 1 0 1 01 1 ( ) 1 ( ) ( ) l s s pLPc s s s jMm m N pLP pMN MN l l j i j M iT iTm MN m MN s p pLPc pMN MNT l i l i si T i Ts u i u u T u u t dt u t dt u TT ( )pLPcu t
- 18. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Wave Variables – Controller Interface • Digital controllers can be implemented while explicitly allowing for continuous time stability. dp c dp The wave variable transformation relates the discrete time controller "outputs" , to the corresponding "inputs" , as follows: 2 2 1 c c c c c v j y j u j y j I I v j u j y j y j I I
- 19. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Resulting Lag Compensator From IPESH Transform 2 2 Desired Analog Lag Compensator: Application of the IPESH Transform Results In 2 1 2 1 2 1 I c P I I s c I s I s c P I s s H s K K s T z z H s T T H z K K T z s z Z Denote and as the respective z-transforms of and such that . c c c c c c c Y z E z y j e j Y z H z E z
- 20. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Assumptions for Sampling Rate Independent Stability i) : is a continous conic system inside the sector , ii) : is a discrete conic dissipative system inside the sector , iii) a) if 0 then 0< < 1 1 b) if 0 then 0< < 2 p p p p p c c c c c p p p H e y a b H e y a b a a a 1 iv) the networked control system is well posed (no instantaneous loop gains 1). pb
- 21. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Sampling Rate Independent Stability Lemma Lemma 1: For our aforementioned digital control network in which the plant, : and controller : satisfy the conditions of our aforementioned assumptions. If the plant and controller satis p p p c c cH e y H e y fy any one of the following listed set of conditions: I. is inside the sector 0, and is inside the sector 0, ; II. is inside the sector 0, and is inside the sector , such that p p c c p c c c H b H b H H a b 2 TT T T 0 < (or vice-versa); III. is inside the sector , in which 0 and is inside the 1 sector , such that < , < ; then the digital control network : , , c c p p p c c c p c c p p c p a b H a a H a b a a b a H r r y y TT 2is -stable.m c L
- 22. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Additional Assumption for Delay Independent Stability Assume that delays are introduced at the wave-variable interface between the controller and multi rate passive sampler and hold devices (PS:MT / PH:MT ) such that: , , , , 0,1,... s s cd c j p j c j j p j j c j u j u j p j 2 2 and v , Then stability is assured as long as for all , , 0,1,... : i) and ii) holds. Condition i) ensures that always holds. Condition ii) ensures that cd c cd cN N j v j c j j l l j j p j l p l j c j l c l u u 2 2 always holds.cd cN N v v
- 23. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Additional Reading for Proof of Lemma 1 • Kottenstette, N., Hall, J.F., Koutsoukos, X., Sztipanovits, J., Antsaklis, P., “Design of Networked Control Systems Using Passivity”, IEEE Transactions on Control Systems Technology Volume: 21 Issue: 3 2012 pp. 649 - 665 – Lemma 1-I. • Kottenstette, N., LeBlanc, H., Eyisi, E., Koutsoukos, X. “Multi-Rate Networked Control of Conic (Dissipative) Systems,” 2011 ACC pp. 274-280 (TR: ISIS-09-108) – Lemma 1-II, 1-III.
- 24. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application I: Networked Control of a Robotic System - Robot Gravity Compensated Robotic systems from the torque to joint velocity output are inside the sector 0, . Notation & Assumptions: ( ) : joint angles, (t): joint torques, ( ( )) : joint torques due to grav t g t T T T ity and joint position ( ( )) : mass matrix C ( ) : matrix of centrifugal and Coriolis effects - 2 2 2 0. Dynamics: ( ) , 0 . u p u p M t M M t C M C M C M C g M C g M C pH ( )py t p I
- 25. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application I: Networked Control of a Robotic System - Robot T T T T T T T T T T 0 Use Lyapunov Function: 1 ( ( )) 0, 0. 2 1 ( ( )) 2 1 ( ( )) 2 1 ( ( )) 2 2 ( ( )) ( ( )) ( (0)) s u p u p u p NT s V t M V t M M V t C M V t M C V t dt V NT V T T 0 T T 0 0 1 1 1 (0) inside sector 0, s s s NT u p NT NT u p p p dt dt dt V p I
- 26. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application I: Networked Control of a Robotic System - Controller T T 1 1 Synthesize Passive MIMO Lag Type Control Law Using inner product equivalent sample and hold (IPESH). Passive CT Control Law ( 0, 0): ( ) ( ), ( ) ( ) ( ) Notation: [ ] p p d d uc p d d K K K K x t e t t K x t K e t e j j 1 1 ( 1) 1 1 1 1 ; [ ] [ ] [ ] Synthesized Passive DT Control Law [ ] : 1 ( ) [ ] ,( 1) , [ ] ( ) [ 1] [ ] [ ] [ ] [ ] [ ] 2 s s sr c uc pc j MT s s uc uc s jMT s s uc p p d j e j e j j G e j e t e j t jMT j MT j t dt T x j x j MT e j MT j K x j K K e j cH j j j j j j cy j ce j
- 27. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application I: Networked Control of a Robotic System - Controller 1 1 1 1 1 1 If >0 then : [ ] is insided the sector 0, . Denote: ; 2 Resulting Strictly Output Passive DT Control Law: [ 1] [ ] [ ] [ ] [ ] c c uc c s p p d c p c s p s c s p uc p H e i i T D K K G I D x i I T G K x i T I T G D e i i G K x i G 1[ ]pD e i cH j j j j j j cy j ce j
- 28. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application I: Networked Control of a Robotic System - Controller 1 1 1 1 1 1 1 1 1 1 Accounting for wave variables and Denote: ; 2 2 1 , , , 2 Resulting DT Control c c s s c p d sp p d sp sp c s p sp s c s p s fe p fe p d u j v j T T G I K K D G K K G I D I T G K T I T G D T C G G K D G G K K Law: 1 1 2 [ 1] [ ] [ ] 2 2 [ ] [ ] sp sp fe sp fe c sr c c fe fe c sr x j C x j I D u j j v j u j C x j D u j j
- 29. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application I: Networked Control of a Robotic System - Setup • Pioneer 3 (P3) arm simulated on PC Host 1 - Plant. • Digital Control Law implemented on PC Host 2 – Controller • Wave variables communicated using TCP/IP over wireless network subject to disturbance node (D1, D2, D3, D4) flood attacks. cu j cdv j cv j cdu j
- 30. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application I: Networked Control of a Robotic System - Parameters Nominal Position Tracking Response (no steady-state tracking error) Control Tunning Rule: 1 1. Approx. Plant , in which is the inertia around joint 1. 2. Approx. Controller G 3. Desire and phase margin of degrees. pm p d c c s G s Js J k k s s s N MT 2 45 Therefore: i) , 5 ii) , iii) 1 c c p d p c J k k k 2 80, 2, .293 kg-m , .1 s, 1.0 6, 0.5, 8.02, 4.1 1, 1. s c p p d N J T e k k M
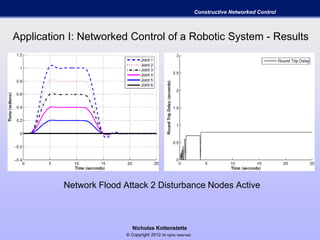
- 31. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application I: Networked Control of a Robotic System - Results Network Flood Attack 2 Disturbance Nodes Active
- 32. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application I: Networked Control of a Robotic System - Results Network Flood Attack 4 Disturbance Nodes Active
- 33. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application I: Networked Control of a Robotic System - Summary • Exploited passive relationships between the control torque and angular velocity of the robots joints. • Synthesized a DT passive lag compensator which is effective in controlling the angular joint position of the robotic arm which requires only the exchange of angular velocity of the joints. • The use of wave variables ensures system stability while allowing for system performance to degrade gradually as the round trip delays increases. • Stability is assured due to Lemma 1-I. • See also: Kottenstette, N., Hall, J.F., Koutsoukos, X., Sztipanovits, J., Antsaklis, P., “Design of Networked Control Systems Using Passivity”, IEEE Transactions on Control Systems Technology Volume: 21 Issue: 3 2012 pp. 649 – 665.
- 34. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application II: Telemanipulation of Haptic Paddles - Overview • Two delta robots (Novint Falcons) can be considered as individual entities in a diagonalized point mass plant model. • A velocity feedback loop applied to each robot renders each robot to be constrained to be interior conic with position as the output. • A passivity preserving orthogonal rotation is applied at the controller side in order to allow each robot to track each other.
- 35. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application II: Telemanipulation of Haptic Paddles – Lemma 1-III 2 2 For our digital control network if: III. is inside the sector , in which 0 and is inside the sector , such that and 1 then the digital control network is stable. p p p c c c p c m c p H a a H a b a a b L a
- 36. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application II: Telemanipulation of Haptic Paddles - Plant Model T TT T 6 T T 6 1 2 1 2: , , , , , : is inside the sector , . p p p p p p p p p ps pl p p p H e y e e e y y y MMT K H e y 1,2l
- 37. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application II: Telemanipulation of Haptic Paddles - Controller Model T 0 is inside the21 , , 2 sector ,2 0 c c c c c c c c c a b I I I R R R I K a b a bI I I a b 1,2l
- 38. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application II: Telemanipulation of Haptic Paddles - Results 2 Parameter Summary: 1, 0.164 kg =1, , K 1 , p ps p c c M M MMT a b
- 39. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application II: Telemanipulation of Haptic Paddles - Proof 1 1 2 2 0 2 2 is inside the sector , . Since 2 2 0 we can consider the concatenation result : is inside the sector , : max , c c c c c c c c c c c c c c c l l a b a b I u y K a b a b a by I u a b a b H u y a b a b a b 1 1 2 2 2 2 2 2 min , 1,2 , , 2 44 Since 0 4 min , , since 4 4 4 l l c c c c l l c c c c c c c cc c c c c c c c c c c c c c c cc c c c c c c c c c c c c a b a b a bab l a b a b a b a b a b a b a b a ba b a b a b a b a b a b a b a b a ba b a b a b a bab a b a b a b a 2 0 4 then . c c c c c c c c c a b b a b a bab a b a b
- 40. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application II: Telemanipulation of Haptic Paddles - Summary • Demonstrated how direct position information can be exchanged over a network in order to create leader-follower haptic systems. • Using an orthogonal rotation matrix we derived a low complexity control law which works within our network control architecture to allow each paddle to track each other. • The use of wave variables ensures system stability while allowing for system performance to degrade gradually as the round trip delays increases. • Stability is assured due to Lemma 1-III. • Kottenstette, N., LeBlanc, H., Eyisi, E., Koutsoukos, X. “Multi-rate networked control of conic (dissipative) systems,” 2011 ACC pp. 274-280 (TR: ISIS-09-108).
- 41. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application III: Networked Coordination of Robotic Arms - Overview • A wave variable networking interface known as a power junction (PJ) is used to interconnect a single lag compensator to multiple (2) robotic arms. • The PJ and lag compensator ensure that each robotic arm will track each other • A classic PD controller is applied to each robotic arm, and a high pass filtered output is augmented to the position output of each arm in order to assure passivity while allowing position tracking at steady state operation. • Stability is assured through the use of wave variables and constraining the controllers and robotic arms interfaced to the network to possess a strictly output passive mapping.
- 42. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application III: Networked Coordination of Robotic Arms - Overview • Novint Falcon paddle used by human operator to provide reference to Crust Crawler robotic arms. • Three Host Computers are used: Robot 1; Robot 2; & Network Controller which is interfaced to haptic paddle. • Communication between devices through wave variables over TCP/IP.
- 43. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application III: Networked Coordination of Robotic Arms - Architecture Lag Compensator Robot 2 (rendered SOP) Power Junction Robot 1 (rendered SOP) 1
- 44. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application III: Networked Coordination of Robotic Arms - Robots Derivative Filter: IPESHˆ 1 1 1ˆ , exp . High Pass Filter: IPESH 1 1 , exp . s s s s s H s s p z H z T z p T p s H s s p z H z T z p p T Robot
- 45. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application III: Networked Coordination of Robotic Arms - PJ 1 1 2 2 3 3Wave variable pairs: , , , , , power-output pairs: , , 1,..., , 1 power-input pairs: , , 1,..., , 3 , , , , 1,...,s j j k k m j k j k s u v u v u v u v j m m u v k m n n u u v v l m 2 1 11 1 1 The outgoing waves are computed from the incoming waves v as follows: sf , sf sgn , 2,3 . 3 1 l l l l l l k j m m mj jj j v k v jm jjj v v v v v v k n mv 2 3 31 21 1 2 1 2 1 The outgoing waves are computed from the incoming waves as follows: sf , sf sgn sf sgn . l l l l l l l l j k n n nkk m kk m u j u k u k kn k k m kkk m u u u u u u u u u mu
- 46. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application III: Networked Coordination of Robotic Arms – Lag Comp. 1 1 ( ) 1 . 2 1 In order to account for scaling effects of PJ, upsamplers and downsamplers ( ) select . s c s T z H z k z M n m k m
- 47. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application III: Networked Coordination of Robotic Arms – Experimental
- 48. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application III: Networked Coordination of Robotic Arms – Experimental • Open-Loop Approach Involves Transmitting only a desired setpoint to each robot which originated from the haptic paddles setpoint interface. • It is clear that the lag compensator and PJ network allow for improved tracking between each robotic arm (similar results for Joints 1 and 2).
- 49. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Application III: Networked Coordination of Robotic Arms – Summary • A PJ and single lag compensator makes it possible to coordinate motion of (n-m) robotic arms in spite of network time delay. • Demonstrated that a high pass filter can be augmented to the position output of the robot in order to derive a strictly output passive robotic interface which allows for steady state reference tracking. See Also: 1. Kottenstette, N., Hall, J.F., Koutsoukos, X., Antsaklis, P., “Digital Control of Multiple Discrete Passive Plants Over Networks,” International Journal of Systems, Control and Communications, Vol. 3, No. 2, pp. 194 – 228 April 2011. 2. Koutsoukos, X., Kottenstette, N., Hall, J., Eyisi, E., Leblanc, H., Porter, J., Sztipanovits, J., “A Passivity Approach for Model-Based Compositional Design of Networked Control Systems,”, ACM Transactions on Embedded Computing Systems, Special Issue on the Synthesis of Cyber-Physical Systems Volume 11 Issue 4, December 2012 Article No. 75. 3. Kottenstette, N., Hall, J.F., Koutsoukos, X., Sztipanovits, J., Antsaklis, P., “Design of Networked Control Systems Using Passivity”, IEEE Transactions on Control Systems Technology Volume: 21 Issue: 3 2012 pp. 649 – 665.
- 50. Nicholas Kottenstette © Copyright 2012 All rights reserved. Constructive Networked Control Conclusions • Interior conic system formulation allows numerous systems to be modeled and considered for low complexity control laws including robotic and quadrotor systems. • Multirate digital control architectures for these systems can be realized with wave variables and novel signal processing abstractions such as the PS, PH, and PJ. • Questions?


![Nicholas Kottenstette
© Copyright 2012 All rights reserved.
Constructive Networked Control
Continuous Time (CT) Interior Conic Systems
0 0 0
( ) ( ) ( ( ) ( ) ( ) () ) 0
T T T
T T T
p p p p p py t y t dt a b y t u t dt ab u t u t dt
2 2
2 2) ,|| ( ) || ( || ( ) || 0T p p p p p p T
T
p py a b uy bu a
2
passive systems are inside the sector [0, ],
strictly input passive systems are inside the sector [ , ,
strictly output passive systems are in
] 0
]
-stable systems are in
side the sect
sid
or [0,
e thm
a
b
L
b
a
e sector [a,b] , .a b
Interior conic systems are inside the sector
0
[ , ]
b
a b
a ](https://image.slidesharecdn.com/705ccdf7-5506-4689-be7c-b4c0ef2ddcb2-160114164804/85/ConstructiveControlRobotsAbridged-3-320.jpg)
![Nicholas Kottenstette
© Copyright 2012 All rights reserved.
Constructive Networked Control
Discrete Time (DT) Interior Conic Systems
1
0
1 1
0 0
( ) ( ) ( ( ) ( ) ( ) () ) 0
N N
T T T
p p p p p p
i
N
ii
y i y i a b y i u i ab u i u i
2 2
2 2) ,|| ( ) || ( || ( ) || 0N p p p p p p N
N
p py a b uy bu a
2
passive systems are inside the sector [0, ],
strictly input passive systems are inside the sector [ , ,
strictly output passive systems are in
] 0
]
-stable systems are in
side the sect
sid
or [0,
e thm
a
b
l
b
a
e sector [a,b] , .a b
Interior conic systems are inside the sector
0
[ , ]
b
a b
a ](https://image.slidesharecdn.com/705ccdf7-5506-4689-be7c-b4c0ef2ddcb2-160114164804/85/ConstructiveControlRobotsAbridged-4-320.jpg)
![Nicholas Kottenstette
© Copyright 2012 All rights reserved.
Constructive Networked Control
Properties: Interior Conic Systems – Sum Rule
1 1 1:H u y
1u
2 2 2:H u y
1y
2u
u
1 2y y y
2y
1 1inside [ , ]a b
2 2inside [ , ]a b
1 2 1 2: inside the sector ,H u y a a b b ](https://image.slidesharecdn.com/705ccdf7-5506-4689-be7c-b4c0ef2ddcb2-160114164804/85/ConstructiveControlRobotsAbridged-5-320.jpg)
![Nicholas Kottenstette
© Copyright 2012 All rights reserved.
Constructive Networked Control
Properties: Interior Conic Systems – Scaling Rule
:H ku y
inside [ , ]a b
ku y
: inside the sector , , if 0
: inside the sector , , if 0
H u y ka kb k
H u y kb ka k
](https://image.slidesharecdn.com/705ccdf7-5506-4689-be7c-b4c0ef2ddcb2-160114164804/85/ConstructiveControlRobotsAbridged-6-320.jpg)


![Nicholas Kottenstette
© Copyright 2012 All rights reserved.
Constructive Networked Control
Sufficient Condition for Feedback Stability of
Interior Conic Systems
Dkd
D
D
D cl
If : is inside the sector [ , ] ([0, ]),
, 0 and the feedback law is
( ) ( ( ) ( )) in which the gain satisfies:
1 1
when 0;
1
when 0 then : is stable.
d
d
H a b
a b b
t k t t
k a
b a
k a H
b
‘D-Term’](https://image.slidesharecdn.com/705ccdf7-5506-4689-be7c-b4c0ef2ddcb2-160114164804/85/ConstructiveControlRobotsAbridged-9-320.jpg)
![Nicholas Kottenstette
© Copyright 2012 All rights reserved.
Constructive Networked Control
Feedback Stability Result for Cascades of
Interior Conic Systems
The following control structure, typically exploited in robotic
control applications is stable under the following set of conditions.
d
cl : dH Pkd
cl cl
cl
P
P P
If : is inside the sector [0, ] ([0,1]),
0 and : is inside the sector [0, ] ([0, ]),
0 and the feedback law is ( ) ( ( ) ( ))
in which the gain satisfies 0 ,then the syst
d
d d
H b
b H b
b t k t t
k k
em is stable.
‘P-Term’](https://image.slidesharecdn.com/705ccdf7-5506-4689-be7c-b4c0ef2ddcb2-160114164804/85/ConstructiveControlRobotsAbridged-10-320.jpg)


![Nicholas Kottenstette
© Copyright 2012 All rights reserved.
Constructive Networked Control
Wireless Networked Control Architecture for Conic Systems
• Render robotic system dynamics (Hp) To remain inside the
sector [a,b].
• Architecture allows for accommodation of time varying
channel capacity (due to communication faults/uncertainty)
• If a >=0 and b is finite, then use discrete time lag
compensator (Hc) to control 𝑦𝑝(t).](https://image.slidesharecdn.com/705ccdf7-5506-4689-be7c-b4c0ef2ddcb2-160114164804/85/ConstructiveControlRobotsAbridged-13-320.jpg)












![Nicholas Kottenstette
© Copyright 2012 All rights reserved.
Constructive Networked Control
Application I: Networked Control of a Robotic System - Controller
T T
1 1
Synthesize Passive MIMO Lag Type Control Law Using
inner product equivalent sample and hold (IPESH).
Passive CT Control Law ( 0, 0):
( ) ( ), ( ) ( ) ( )
Notation: [ ]
p p d d
uc p d
d
K K K K
x t e t t K x t K e t
e j j
1
1
( 1)
1 1
1
1
; [ ] [ ] [ ]
Synthesized Passive DT Control Law [ ] :
1
( ) [ ] ,( 1) , [ ] ( )
[ 1] [ ] [ ]
[ ] [ ] [ ]
2
s
s
sr c uc
pc
j MT
s s uc uc
s jMT
s
s
uc p p d
j e j e j j
G e j
e t e j t jMT j MT j t dt
T
x j x j MT e j
MT
j K x j K K e j
cH
j j
j
j
j
j
cy j
ce j](https://image.slidesharecdn.com/705ccdf7-5506-4689-be7c-b4c0ef2ddcb2-160114164804/85/ConstructiveControlRobotsAbridged-26-320.jpg)
![Nicholas Kottenstette
© Copyright 2012 All rights reserved.
Constructive Networked Control
Application I: Networked Control of a Robotic System - Controller
1 1
1
1 1
1
If >0 then : [ ] is insided the sector 0, .
Denote: ;
2
Resulting Strictly Output Passive DT Control Law:
[ 1] [ ] [ ]
[ ] [ ]
c c uc
c
s
p p d c p
c s p s c s p
uc p
H e i i
T
D K K G I D
x i I T G K x i T I T G D e i
i G K x i G
1[ ]pD e i cH
j j
j
j
j
j
cy j
ce j](https://image.slidesharecdn.com/705ccdf7-5506-4689-be7c-b4c0ef2ddcb2-160114164804/85/ConstructiveControlRobotsAbridged-27-320.jpg)
![Nicholas Kottenstette
© Copyright 2012 All rights reserved.
Constructive Networked Control
Application I: Networked Control of a Robotic System - Controller
1
1 1
1
1 1 1 1
1 1
Accounting for wave variables and
Denote: ;
2 2
1
, ,
,
2
Resulting DT Control
c c
s s
c p d sp p d
sp sp c s p sp s c s p
s
fe p fe p d
u j v j
T T
G I K K D G K K
G I D I T G K T I T G D
T
C G G K D G G K K
Law:
1 1 2
[ 1] [ ] [ ]
2 2
[ ] [ ]
sp sp fe sp fe c sr
c c fe fe c sr
x j C x j I D u j j
v j u j C x j D u j j
](https://image.slidesharecdn.com/705ccdf7-5506-4689-be7c-b4c0ef2ddcb2-160114164804/85/ConstructiveControlRobotsAbridged-28-320.jpg)