Continuous probability distribution

Continuous Probability Distribution
Bipul Kumar Sarker
Lecturer
BBA Professional
Habibullah Bahar University College
Chapter-04

History of Normal Distribution
The normal distribution was first discovered by De Moivre (English
Mathematician) in 1733 as limiting case of binomial distribution. Later it
was applied in natural and social science by Laplace (French
Mathematician) in 1777. The normal distribution is also known as Gaussian
distribution in honor of Karl Friedrich Gauss(1809).
Bipul Kumar Sarker, Lecturer (BBA Professional), HBUC

3.3.1 Definition Of Normal Distribution:
A continuous random variable X is said to follow normal distribution with mean m and
standard deviation s, if its probability density function is define as follow,
Note:
The mean m and standard deviation s are called the parameters of Normal
distribution. The normal distribution is expressed by 𝑋~𝑁 𝜇, 𝜎2 .

3.3.2 Condition of Normal Distribution:
i. Normal distribution is a limiting form of the binomial distribution under the
following conditions.
a. n, the number of trials is indefinitely large ie., 𝑛 → ∞ and
b. Neither p nor q is very small.
ii. Normal distribution can also be obtained as a limiting form of Poisson distribution
with parameter 𝑚 → ∞
iii. Constants of normal distribution are mean = m, variation = 𝜎2, Standard deviation = s

3.3.3 Normal Probability Curve:
The curve representing the normal distribution is called the normal probability
curve. The curve is symmetrical about the mean (m), bell-shaped and the two tails
on the right and left sides of the mean extends to the infinity. The shape of the curve
is shown in the following figure.

3.3.4 Properties of Normal Distribution:
i. The normal curve is bell shaped and is symmetric at x = m.
ii. Mean, median, and mode of the distribution are coincide
i.e., Mean = Median = Mode = m
iii. It has only one mode at x = m (i.e., unimodal)
iv. Since the curve is symmetrical, Skewness = 𝛽1 = 0 and Kurtosis = 𝛽2= 3
v. The points of inflection are at x = m ± s

vi. The maximum ordinate occurs at x = m and its value is
1
𝜎 2𝜋
vii. The x axis is an asymptote to the curve
i.e. the curve continues to approach but never touches the x axis
viii. The first and third quartiles are equidistant from median.
ix. The mean deviation about mean is 0.8 s

X. Quartile deviation = 0.6745 s
XI. If X and Y are independent normal variates with mean 𝜇1 and 𝜇2, and variance 𝜎1 And
𝜎2 respectively then their sum (X + Y) is also a normal variate with mean (𝜇1 + 𝜇2) and
variance 𝜎1
2 + 𝜎2
2
XII. Area Property P(m - s < Z < m + s) = 0.6826
P(m - 2s < Z < m + 2s) = 0.9544
P(m - 3s < Z < m + 3s) = 0.9973

3.3.5 Standard Normal distribution:
Let X be random variable which follows normal distribution with mean m and
variance 𝜎2
.The standard normal variate is defined as 𝑍 =
𝑋−𝜇
𝜎
which follows
standard normal distribution with mean 0 and standard deviation 1 i.e., Z ~ N(0,1).
The standard normal distribution is given by
𝚽 𝒁 =
𝟏
𝟐𝝅
𝒆−
𝟏
𝟐
𝒛 𝟐
; −∞ < 𝒁 < ∞
The advantage of the above function is that it doesn’t’ contain any parameter.
This enable us to compute the area under the normal probability curve.

3.3.6 Area properties of Normal curve:
The total area under the normal probability curve is 1. The curve is also called
standard probability curve. The area under the curve between the ordinates at x = a
and x = b where a < b, represents the probabilities that x lies between x = a and x = b
i.e., P(a  x  b)

To find any probability value of x, we first standardize it by using 𝑍 =
𝑋−𝜇
𝜎
, and use
the area probability normal table.

Example:
The probability that the normal random variable x to lie in the interval (m-s , m+s) is given by,
1.

2.

3.

The probability that a normal variate x lies outside the range m ± 3s is given by
Thus we expect that the values in a normal probability curve will lie between the range
m ± 3s, though theoretically it range from -  to .

Example -01
Find the probability that the standard normal variate lies between 0 and 1.56
Solution:
−∞ 𝑍 = 0 𝑍 = 1.56 +∞
P(0< z< 1.56) = Area between z = 0 and z = 1.56
= 0.4406 (from table)

Example-02
Find the area of the standard normal variate from –1.96 to 0.
Solution:
−∞ 𝑍 = −1.96 𝑍 = 0 +∞
Area between z = 0 & z =-1.96
is same as the area z = 0 to z = 1.96
P(-1.96 < z < 0) = P(0 < z < 1.96) (by symmetry)
= 0.4750 (from the table)

P(z >0.25) = P(0<z < ) – P(0<z<0.25)
= 0.5000 - 0.0987 (from the table)
= 0.4013
Example-03
Find the area to the right of z = 0.25
Solution:

Example-04
Find the area to the left of z = 1.5
Solution:
P(z < 1.5) = P( -  < z < 0 ) + P( 0 < z < 1.5 )
= 0.5 + 0.4332 (from the table)
= 0.9332

Example-05
Find the area of the standard normal variate
between –1.96 and 1.5
Solution:
P(-1.96 < z < 1.5) = P(-1.96 < z < 0) + P(0 < z < 1.5)
= P(0 < z < 1.96) + P(0 < z < 1.5)
= 0.4750 + 0.4332 (from the table)
= 0.9082

Example-06
Given a normal distribution with m = 50 and s = 8, find the probability that x assumes a
value between 42 and 64.
Solution:
Given that m = 50 and s = 8
The standard normal variate, 𝑍 =
𝑋−𝜇
𝜎
If X = 42, 𝑍 =
42−50
8
= −1
If X = 64, 𝑍 =
64−50
8
= 1.74

P(42 < x < 64) = P(-1 < z <1.75)
= P(-1< z < 0) + P(0 < z <1.95)
= P(0<z<1) + P (0 < z <1.75) (by symmetry)
= 0.3413 +0 .4599 (from the table)
= 0 .8012
If X = 42, 𝑍 =
42−50
8
= −1
If X = 64, 𝑍 =
64−50
8
= 1.74

Example-07
Students of a class were given an aptitude test. Their marks were found to be normally
distributed with mean 60 and standard deviation 5. What percentage of students scored.
i) More than 60 marks
ii) Less than 56 marks
iii)Between 45 and 65 marks

i. The standard normal variate,𝑍 =
𝑋−𝜇
𝜎
If X = 60, 𝑍 =
60−60
5
= 0
P(x > 60) = P(z > 0)
= P(0 < z <  )
= 0.5
Hence the percentage of students scored more than 60 marks is 0.5×100 = 50 %
Solution:
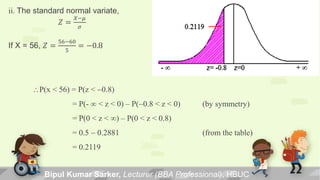
Given that mean = m = 60 and standard deviation = s = 5

ii. The standard normal variate,
𝑍 =
𝑋−𝜇
𝜎
If X = 56, 𝑍 =
56−60
5
= −0.8
P(x < 56) = P(z < -0.8)
= P(-  < z < 0) – P(-0.8 < z < 0) (by symmetry)
= P(0 < z < ) – P(0 < z < 0.8)
= 0.5 - 0.2881 (from the table)
= 0.2119

Hence the percentage of students score less than 56 marks is 0.2119×100 = 21.19 %

−∞ 𝑍 = −3 𝑍 = 0 𝑍 = 1 +∞
iii. The standard normal variate, 𝑍 =
𝑋−𝜇
𝜎
If X = 45, 𝑍 =
45−60
5
= −3
If X = 65, 𝑍 =
65−60
5
= 1
P(45 < x < 65) = P(-3 < z < 1)
= P(-3 < z < 0 ) + P ( 0 < z < 1)
= P(0 < z < 3) + P(0 < z < 1) ( by symmetry)
= 0.4986 + 0.3413 (from the table)
= 0.8399

Hence the percentage of students scored between 45 and 65 marks is 0.8399×100 = 83.99 %

Example-08
X is normal distribution with mean 2 and standard deviation 3. Find the value of the
variable x such that the probability of the interval from mean to that value is 0.4115
Solution:
Given m = 2, s = 3
Suppose z1 is required standard value,
Thus 𝑃 (0 < 𝑧 < 𝑧1) = 0.4115
From the table the value corresponding to the area 0.4115 is 1.35 that is 𝑧1 = 1.35

Here, 𝑧1 =
𝑋−𝜇
𝜎
⇒ 1.35 =
𝑋 − 2
3
⇒ 1.35 × 3 + 2 = 𝑋
𝑋 = 6.05

Continuous probability distribution

More Related Content

What's hot (20)

Similar to Continuous probability distribution (20)

More from Habibullah Bahar University College (9)

Recently uploaded (20)

Continuous probability distribution