Ctrie Data Structure
- 1. Concurrent Tries with Efficient Non-blocking Snapshots Aleksandar Prokopec Phil Bagwell Martin Odersky École Polytechnique Fédérale de Lausanne Nathan Bronson Stanford
- 2. Motivation val numbers = getNumbers() // compute square roots numbers foreach { entry => x = entry.root n = entry.number entry.root = 0.5 * (x + n / x) if (abs(entry.root - x) < eps) numbers.remove(entry) }
- 3. Hash Array Mapped Tries (HAMT)
- 4. Hash Array Mapped Tries (HAMT) 0 = 0000002
- 5. Hash Array Mapped Tries (HAMT) 0
- 6. Hash Array Mapped Tries (HAMT) 0 16 = 0100002
- 7. Hash Array Mapped Tries (HAMT) 0 16
- 8. Hash Array Mapped Tries (HAMT) 0 16 4 = 0001002
- 9. Hash Array Mapped Tries (HAMT) 16 0 4 = 0001002
- 10. Hash Array Mapped Tries (HAMT) 16 0 4
- 11. Hash Array Mapped Tries (HAMT) 16 0 4 12 = 0011002
- 12. Hash Array Mapped Tries (HAMT) 16 0 4 12 = 0011002
- 13. Hash Array Mapped Tries (HAMT) 16 0 4 12
- 14. Hash Array Mapped Tries (HAMT) 16 33 0 4 12
- 15. Hash Array Mapped Tries (HAMT) 16 33 0 4 12 48
- 16. Hash Array Mapped Tries (HAMT) 16 0 4 12 48 33 37
- 17. Hash Array Mapped Tries (HAMT) 16 4 12 48 33 37 0 3
- 18. Hash Array Mapped Tries (HAMT) 4 12 16 20 25 33 37 0 1 8 9 3 48 57
- 19. Immutable HAMT •used as immutable maps in functional languages 4 12 16 20 25 33 37 0 1 8 9 3
- 20. Immutable HAMT •updates rewrite path from root to leaf 4 12 16 20 25 33 37 0 1 8 9 3 4 12 8 9 11 insert(11)
- 21. Immutable HAMT •updates rewrite path from root to leaf 4 12 16 20 25 33 37 0 1 8 9 3 4 12 8 9 11 insert(11) efficient updates - logk(n)
- 22. Node compression 48 57 48 57 1 0 1 0 48 57 1 0 1 0 48 57 10 BITPOP(((1 << ((hc >> lev) & 1F)) – 1) & BMP)
- 23. Node compression 48 57 48 57 1 0 1 0 48 57 1 0 1 0 48 57 10 48 57
- 24. Ctrie Can mutable HAMT be modified to be thread-safe?
- 25. Ctrie insert 4 9 12 16 20 25 33 37 0 1 3 48 57 17 = 0100012
- 26. Ctrie insert 4 9 12 16 20 25 33 37 0 1 3 48 57 17 = 0100012 16 17 1) allocate
- 27. Ctrie insert 4 9 12 20 25 33 37 0 1 3 48 57 17 = 0100012 16 17 2) CAS
- 28. Ctrie insert 4 9 12 20 25 33 37 0 1 3 48 57 17 = 0100012 16 17
- 29. Ctrie insert 4 9 12 33 37 0 1 3 48 57 18 = 0100102 16 17 20 25
- 30. Ctrie insert 4 9 12 33 37 0 1 3 48 57 18 = 0100102 16 17 20 25 1) allocate 16 17 18
- 31. Ctrie insert 4 9 12 33 37 0 1 3 48 57 18 = 0100102 20 25 2) CAS 16 17 18
- 32. Ctrie insert 4 9 12 33 37 0 1 3 48 57 18 = 0100102 20 25 2) CAS 16 17 18 Unless…
- 33. Ctrie insert 4 9 12 33 37 0 1 3 48 57 18 = 0100102 16 17 20 25 T1-1) allocate 16 17 18 Unless… 28 = 0111002 T1 T2
- 34. Ctrie insert 4 9 12 0 1 3 18 = 0100102 16 17 20 25 T1-1) allocate 16 17 18 Unless… 28 = 0111002 T1 T2 20 25 28 T2-1) allocate
- 35. Ctrie insert 4 9 12 0 1 3 18 = 0100102 16 17 20 25 T1-1) allocate 16 17 18 28 = 0111002 T1 T2 20 25 28 T2-2) CAS
- 36. Ctrie insert 4 9 12 0 1 3 18 = 0100102 16 17 20 25 T1-2) CAS 16 17 18 28 = 0111002 T1 T2 20 25 28 T2-2) CAS
- 37. Ctrie insert 4 9 12 0 1 3 18 = 0100102 16 17 20 25 16 17 18 28 = 0111002 T1 T2 20 25 28 Lost insert!
- 38. Ctrie insert – 2nd attempt 4 9 12 0 1 3 16 17 20 25 Solution: I-nodes
- 39. Ctrie insert – 2nd attempt 4 9 12 0 1 3 16 17 20 25 18 = 0100102 28 = 0111002 T1 T2
- 40. Ctrie insert – 2nd attempt 4 9 12 0 1 3 16 17 T1 T2 20 25 18 = 0100102 28 = 0111002 16 17 18 20 25 28 T2-1) allocate T1-1) allocate
- 41. Ctrie insert – 2nd attempt 4 9 12 0 1 3 16 17 T1 T2 20 25 16 17 18 20 25 28 T2-2) CAS T1-2) CAS
- 42. Ctrie insert – 2nd attempt 4 9 12 0 1 3 16 17 18 20 25 28
- 43. Ctrie insert – 2nd attempt 4 9 12 0 1 3 16 17 18 20 25 28 Idea: once added to the Ctrie, I-nodes remain present.
- 44. Ctrie insert – 2nd attempt 4 9 12 0 1 3 16 17 18 20 25 28 Remove operation supported as well - details in the paper.
- 45. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28
- 46. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28 size = 0
- 47. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28 size = 0
- 48. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28 size = 0
- 49. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28 size = 0
- 50. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28 size = 1
- 51. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28 size = 2
- 52. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28 size = 3
- 53. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28 size = 5
- 54. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28 size = 5 actual size = 12
- 55. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28 size = 5 0 1 actual size = 12
- 56. Ctrie size 4 9 12 0 1 3 16 17 18 20 25 28 size = 5 0 1 CAS actual size = 11
- 57. Ctrie size 4 9 12 16 17 18 20 25 28 size = 5 0 1 actual size = 11
- 58. Ctrie size 4 9 12 16 17 18 20 25 28 size = 6 0 1 actual size = 11
- 59. Ctrie size 4 9 12 16 17 18 20 25 28 size = 6 0 1 actual size = 11 19
- 60. Ctrie size 4 9 12 16 17 18 20 25 28 size = 6 0 1 actual size = 11 16 17 18 19
- 61. Ctrie size 4 9 12 16 17 18 20 25 28 size = 6 0 1 actual size = 12 16 17 18 19 CAS
- 62. Ctrie size 4 9 12 20 25 28 size = 6 0 1 actual size = 12 16 17 18 19
- 63. Ctrie size 4 9 12 20 25 28 size = 6 0 1 actual size = 12 16 17 18 19
- 64. Ctrie size 4 9 12 20 25 28 size = 7 0 1 actual size = 9 16 17 18 19
- 65. Ctrie size 4 9 12 20 25 28 size = 8 0 1 actual size = 12 16 17 18 19
- 66. Ctrie size 4 9 12 20 25 28 size = 9 0 1 actual size = 12 16 17 18 19
- 67. Ctrie size 4 9 12 20 25 28 size = 10 0 1 actual size = 12 16 17 18 19
- 68. Ctrie size 4 9 12 20 25 28 size = 11 0 1 actual size = 12 16 17 18 19
- 69. Ctrie size 4 9 12 20 25 28 size = 12 0 1 actual size = 12 16 17 18 19
- 70. Ctrie size 4 9 12 20 25 28 size = 13 0 1 actual size = 12 16 17 18 19
- 71. Ctrie size 4 9 12 20 25 28 size = 13 0 1 actual size = 12 16 17 18 19 But the size was never 13!
- 72. Global state information 4 9 12 20 25 28 0 1 16 17 18 19 •size •find •filter •iterator
- 73. Global state information 4 9 12 20 25 28 0 1 16 17 18 19 •size •find •filter •iterator snapshot
- 74. Snapshot using locks 4 9 12 20 25 28 0 1 16 17 18 19
- 75. Snapshot using locks 4 9 12 20 25 28 0 1 16 17 18 19 •copy expensive
- 76. Snapshot using locks 4 9 12 20 25 28 0 1 16 17 18 19 •copy expensive •not lock-free
- 77. Snapshot using locks 4 9 12 20 25 28 0 1 16 17 18 19 •copy expensive •not lock-free •can insert or remove remain lock-free? 0 1 2 CAS
- 78. Snapshot using locks 4 9 12 20 25 28 0 1 16 17 18 19 •copy expensive •not lock-free •can insert or remove remain lock-free? 0 1 2 CAS
- 79. Snapshot using logs 4 9 12 20 25 28 0 1 16 17 18 19 •keep a linked list of previous values in each I-node
- 80. Snapshot using logs 4 9 12 20 25 28 0 1 16 17 18 19 0 1 2 •keep a linked list of previous values in each I-node
- 81. Snapshot using logs 4 9 12 20 25 28 0 1 16 17 18 19 •keep a linked list of previous values in each I-node •when is it safe to delete old entries? 0 1 2
- 82. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 root
- 83. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 root
- 84. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 snapshot! root
- 85. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 snapshot! #2 root 1) create new I-node at #2
- 86. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 snapshot! #2 root 2) set snapshot snapshot #1
- 87. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 snapshot! #2 root 3) CAS root to new I-node snapshot #1
- 88. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 subsequent insert #2 root snapshot #1 2
- 89. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 subsequent insert #2 root snapshot #1 2 generation #2 - ok!
- 90. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 subsequent insert #2 root snapshot #1 2 generation #1 not ok, too old!
- 91. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 subsequent insert #2 root 1) create updated node at #2 snapshot #1 2 #2 #2
- 92. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 subsequent insert #2 root 2) CAS to the updated node snapshot #1 2 #2 #2
- 93. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 subsequent insert #2 root snapshot #1 2 #2 #2 #1 too old!
- 94. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 subsequent insert #2 root snapshot #1 2 #2 #2 4 9 12 #2 1) create updated node at #2
- 95. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 subsequent insert #2 root snapshot #1 2 #2 #2 4 9 12 #2 2) CAS
- 96. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 subsequent insert #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 finally, create a new leaf and CAS
- 97. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 another insert #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 3
- 98. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 another insert #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 0 1 2 3
- 99. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 But... this won't really work... why? #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 0 1 2 3
- 100. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 0 1 2 3 T2: remove 19 16 17 18
- 101. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 0 1 2 3 T2: remove 19 16 17 18 CAS
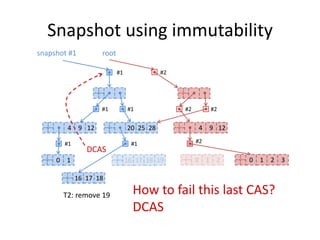
- 102. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 0 1 2 3 T2: remove 19 16 17 18 CAS How to fail this last CAS?
- 103. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 0 1 2 3 T2: remove 19 16 17 18 DCAS How to fail this last CAS? DCAS
- 104. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 0 1 2 3 T2: remove 19 16 17 18 How to fail this last CAS? DCAS - software based DCAS
- 105. Snapshot using immutability 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 0 1 2 3 T2: remove 19 16 17 18 How to fail this last CAS? DCAS - software based ...creates intermediate objects DCAS
- 106. GCAS - generation-compare-and-swap 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 3 T2: remove 19 16 17 18 prev 1) set prev field
- 107. GCAS - generation-compare-and-swap 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 3 T2: remove 19 16 17 18 prev 2) CAS
- 108. GCAS - generation-compare-and-swap 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 3 T2: remove 19 16 17 18 prev 3) read root generation
- 109. GCAS - generation-compare-and-swap 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 3 16 17 18 prev 4) if root generation changed CAS prev to FailedNode(prev) FN
- 110. GCAS - generation-compare-and-swap 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 3 16 17 18 prev 4) if root generation changed CAS prev to FailedNode(prev) FN
- 111. GCAS - generation-compare-and-swap 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 3 16 17 18 prev 5) CAS to previous value FN
- 112. GCAS - generation-compare-and-swap 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 3 16 17 18 prev 4) if root generation unchanged CAS prev to null
- 113. GCAS - generation-compare-and-swap 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 3 16 17 18 4) if root generation unchanged CAS prev to null
- 114. GCAS - generation-compare-and-swap 4 9 12 20 25 28 0 1 16 17 18 19 #1 #1 #1 #1 #1 #2 root snapshot #1 #2 #2 4 9 12 #2 0 1 2 3 1) Replace all CAS with GCAS 2) Replace all READ with GCAS_READ (which checks if prev field is null)
- 115. Snapshot-based iterator def iterator = if (isSnapshot) new Iterator(root) else snapshot().iterator()
- 116. Snapshot-based size def size = { val sz = 0 val it = iterator while (it.hasNext) sz += 1 sz }
- 117. Snapshot-based size def size = { val sz = 0 val it = iterator while (it.hasNext) sz += 1 sz } Above is O(n). But, by caching size in nodes - amortized O(logkn)! (see source code)
- 118. Snapshot-based atomic clear def clear() = { val or = READ(root) val nr = new INode(new Gen) if (!CAS(root, or, nr)) clear() } (roughly)
- 119. Evaluation - quad core i7
- 120. Evaluation – UltraSPARC T2
- 121. Evaluation – 4x 8-core i7
- 123. Conclusion •snapshots are linearizable and lock-free •snapshots take constant time •snapshots are horizontally scalable •snapshots add a non-significant overhead to the algorithm if they aren't used •the approach may be applicable to tree-based lock-free data-structures in general (intuition)
- 124. Thank you!