Decision Trees and Bayes Classifiers
- 1. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up CS-E3210 Machine Learning: Basic Principles Lecture 6: Classification II slides by Alexander Jung, 2017 Department of Computer Science Aalto University, School of Science Autumn (Period I) 2017 1 / 39
- 2. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Outline 1 Intro 2 Decision Trees 3 Bayes Classifiers 4 Wrap Up 2 / 39
- 3. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Enriching our Arsenal of Classifiers in the previous lecture we heard about two important classification methods: LogReg and SVC both are parametric: specified by vector w ∈ Rd and offset b both are discriminative: do not model data generation LogReg and SVC differ in how they fit w and b to X today we widen up our repertoire by considering one non-parametric and one generative method (Bayes classifier) 3 / 39
- 4. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Outline 1 Intro 2 Decision Trees 3 Bayes Classifiers 4 Wrap Up 4 / 39
- 5. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Ski Resort Marketing you are (still) working as marketing manager of a ski resort hard disk full of webcam snapshots (gigabytes of data) want to group them into “winter” and ”summer” images you have only a few hours for this task ... 5 / 39
- 6. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Labeled Webcam Snapshots create dataset X by randomly selecting N = 6 snapshots manually categorise/label them (y(i) = 1 for summer) redness x (i) r and greenness x (i) g turned out to be good features 6 / 39
- 7. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Lets Try LogReg and SVC 7 / 39
- 8. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Now we come across another dataset... there is no good linear classifier 8 / 39
- 9. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up A Decision Tree DT represents a mapping h(·) : X → Y : x → ˆy = h(x) DT consists of nodes and branches between them there are decision nodes (“ ”) and leaf nodes (“ ”) DN test various properties of x = (x1, . . . , xd ) LN represents all vectors x which satisfy several tests LN m corresponds to region Rm ⊆ X 9 / 39
- 10. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up A Decision Node (“ ”) DN tests certain property of features x = (x1, . . . , xd ) e.g. a DN amounts to testing if “x2 > 10?” for binary features (X = {0, 1}d ) a test could be “x1 = 1?” one incoming branch and several outgoing branches 10 / 39
- 11. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up A Leaf Node (“ ”) nodes without any outgoing branch are leaf nodes LN “collects” all vectors x ∈ X which pass every test along the way from root leaf node m corresponds to region Rm ⊆ X 11 / 39
- 12. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up A Decision Tree consider snapshot app with features x = (xr , xg ) 12 / 39
- 13. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Evaluating a Decision Tree start with the test (e.g., x1 < w) at root node based on result of this test follow one of the branches follow branches till a leaf node m is reached datapoints x ending in leaf node m form region Rm ⊆X classify any data point with x ∈ Rm as h(x) = hm 13 / 39
- 14. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Evaluating a Decision Tree Classifier (Picture) 14 / 39
- 15. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Tree Representation of a Classifier feature space X = R2, label space Y = {0, 1} decision tree represents partitioning of feature space: X = R1 ∪ R2 ∪ R3 with R1 :={x1 <w, x2 <w}, R2 :={x1 <w, x2 ≥w}, R3 :={x1 ≥w} hypothesis defined piece-wise constant h(x) = 1 if x ∈ R1 0 if x ∈ R2 1 if x ∈ R3 15 / 39
- 16. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Learning a Decision Tree Growing a Tree how to learn decision tree from data X={x(i), y(i)}N i=1? key recursive property of trees: attaching a tree to a leaf node yields a tree! underlies most decision tree methods (CART,ID3 and C4.5) grow (learn) a tree based on data X which nodes to extend and how long? 16 / 39
- 17. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Learning a Decision Tree Converting Leaf to Decision Node hypothesis based on thresholding individual features xj for simplicity we assume fixed threshold w consider particular leaf node m of a given partial tree Xm ⊆X collects all datapoints (x(i), y(i)) reaching leaf m replace leaf node m by decision node using attribute xj Xm,< is subset of Xm with x (i) j <w Xm,≥ is subset of Xm with x (i) j ≥w 17 / 39
- 18. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Learning a Decision Tree Converting Leaf to Decision Node y n xj <wnode m Xm ✓ X partial tree partial tree grow tree node m< node m Xm,< ✓Xm Xm, ✓Xm 18 / 39
- 19. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Learning a Decision Tree Converting Leaf to Decision Node shall we grow the LN m? which DN should we use for growing? 19 / 39
- 20. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Learning Optimal Classifier for Given Tree consider a given DT each leaf node m represents a region Rm ⊆ X DT induces a partitioning of X into Rm data points ending up in leaf m are classified the same hm DT classifier h(x) = leaf node m hmIRm (x) how to choose hm? 20 / 39
- 21. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up ID Card of Decision Tree Classifiers input/feature space X = Rd label space Y = {0, 1} different choices for the loss function possible hypothesis space H = {h(x) = leaf node m hmIRm (x)} 21 / 39
- 22. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Outline 1 Intro 2 Decision Trees 3 Bayes Classifiers 4 Wrap Up 22 / 39
- 23. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up A Classification Problem data points with features x(i) ∈Rd and labels y(i) ∈{0, 1} classify ˆy = I{h(x) > 1/2} with predictor h(·) ∈ H LogReg and SVC use H = {h(w)(x) = wT x} learn classifier by empirical risk minimization min h(·)∈H E{h(·)|X} = (1/N) N i=1 L((x(i) , y(i) ), h(·)) different loss functions yield different classifiers 23 / 39
- 24. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Minimizing Error Probability eventually, we aim at low error probability P(ˆy = y) using 0/1-loss L((x, y), h(·)) = I(ˆy = y) we can approximate P(ˆy = y) ≈ (1/N) N i=1 L((x(i) , y(i) ), h(·)) the optimal classifier is then obtained by min h(·)∈H N i=1 L((x(i) , y(i) ), h(·)) hard non-convex non-smooth optimization problem ! workaround by using a probabilistic generative model 24 / 39
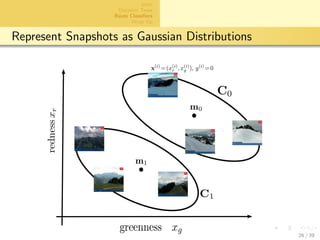
- 25. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up A Probabilistic Generative Model model data as realizations of random variable z = (x, y) label y is a binary (Bernoulli) rv with pmf P(y) given y, features x are Gaussian N(my , Cy ) NOTE: mean my and covariance Cy depends on label y! 25 / 39
- 26. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Represent Snapshots as Gaussian Distributions 26 / 39
- 27. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Parameter Estimation prob. model parametrized by P(y), {my , Cy }y∈{0,1} how to choose parameters using X = {x(i), y(i)}N i=1 maximum likelihood estimates given by P(y) = 1 N N i=1 I(y(i) = y) ˆmy = 1 NP(y) N i=1 I(y(i) = y)x(i) , Cy = 1 NP(y) N i=1 I(y(i) = y)(x(i) −my )(x(i) −my )T . 27 / 39
- 28. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Probabilistic Machine Learning given y, features x are Gaussian N(my , Cy ) NOTE: mean my and covariance Cy depends on label y! for given my and Cy , how to minimize P(ˆy = y) ? choose ˆy as solution of max y∈{0,1} log P(y|x) “maximum a-posteriori” (MAP) how to obtain the posterior prob. P(y|x)? 28 / 39
- 29. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up The Bayes Classifier classify data point x using solution ˆy of max y∈{0,1} log P(y|x) “maximum a-posteriori” (MAP) use Bayes’ rule to obtain posterior probability P(y|x) “posterior” ∝ p(x|y) “likelihood” · P(y) “prior” since p(x|y) = N(my , Cy ), obtain further log P(y|x) = (1/2)(x−my )T C−1 y (x−my )−(1/2) log det(Cy )+log P(y) replace P(y), {my , Cy }y∈{0,1} with estimates ˆP(y), . . . 29 / 39
- 30. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Bayes Classifier Recipe Bayes’ classifier recipe compute parameter estimates Py, { ˆmy , Cy }y∈{0,1} classify according to max posteriori prob ˆy = argmax y∈{0,1} (x− ˆmy )T C−1 y (x− ˆmy )−log det(Cy )+2 log P(y) looks quite simple doesn’t it ? BUT: how accurate can we estimate the parameters? what if Cy singular ? (always the case for N < d) 30 / 39
- 31. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Naive Bayes Classifier require additional structure of parameters e.g., assume Cy = C for all y ∈ {0, 1} (common covariance) additionally assume C diagonal C = σ2 1 0 . . . 0 0 σ2 2 . . . 0 ... ... ... ... 0 0 . . . σ2 d Bayes classifier becomes ˆy = I(h(w,b)(x) ≥ 1/2) with h(w,b)(x) = wT x + b weight vector w and offset b determined by ˆP(y), . . . 31 / 39
- 32. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Outline 1 Intro 2 Decision Trees 3 Bayes Classifiers 4 Wrap Up 32 / 39
- 33. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up What we Learnt Today a non-parametric classification method, i.e., decision trees a generative classification method, i.e., (naive) Bayes classifier considered real-valued features X =Rd and binary classification Y ={0, 1} extend easily to discrete features and more than two classes 33 / 39
- 34. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Decision Trees vs. LogReg, SVC and naive Bayes LogReg, SVC and naive Bayes are parametric methods classifier h(x) identified by parameters w, my , . . . .. LogReg, SVC and naive Bayes differ in how to fit parameters to data X in stark contrast, decision tree classifiers are non-parametric members of H specified using full dataset X ! 34 / 39
- 35. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Parametric or Non-Parametric? non-par. methods require entire dataset for computing h(x)! parametric methods can discard data once parameters are learnt (compression!) e..g, once the parameter w is learnt for LogReg, we don’t need data for computing h(w)(x) 35 / 39
- 36. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Naive Bayes vs. Logistic Regression Bayes classifier models joint distribution p(y, x) generative: obtain a full model for p(y, x) could synthesise new samples by drawing from p(y, x)!!! logistic regression models directly posterior P(y | x) discriminative: no generative model for p(y, x) conceptually reasonable since not mainly interested in p(y, x) 36 / 39
- 37. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Generative or Discriminative? for large sample size N, discriminative methods optimal generative methods might be beneficial for small N 20 30 m ontinuous) 0 20 40 60 0.2 0.25 0.3 0.35 0.4 0.45 m error boston (predict if > median price, continuous) d 3’s, continuous) 0.5 ionosphere (continuous) generalizationerror training size N logistic regression naive Bayes “On Discriminative vs. Generative classifiers: A comparison of logistic regression and naive Bayes”, A. Y. Ng and M. I. Jordan. 37 / 39
- 38. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up Generative or Discriminative? (ctd.) generative classifier (e.g., Bayes classifier) learning based on joint distribution p(y, x) can handle missing values in X works well for small X and accurate model for p(y, x) discriminative classifier (e.g., logistic regression) learning based on conditional distribution P(y | x) no model for prior p(y, x) required! cannot handle missing values in X preferable for large training size or if we dont know good model p(y, x) 38 / 39
- 39. aalto-logo-en-3 Intro Decision Trees Bayes Classifiers Wrap Up What Happens Next? next lecture on how to evaluate (validate) a method fill out post-lecture questionnaire in MyCourses (contributes to grade!) 39 / 39