Declarative Language Definition
- 1. Eelco Visser ECOOP Summer School 2017 Barcelona June 2017 Declarative Language Definition
- 2. /* A program to solve the 8-queens problem */ let var N := 8 type intArray = array of int var row := intArray [ N ] of 0 var col := intArray [ N ] of 0 var diag1 := intArray [N+N-1] of 0 var diag2 := intArray [N+N-1] of 0 function printboard() = (for i := 0 to N-1 do (for j := 0 to N-1 do print(if col[i]=j then " O" else " ."); print("n")); print("n")) function try(c:int) = ( if c=N then printboard() else for r := 0 to N-1 do if row[r]=0 & diag1[r+c]=0 & diag2[r+7-c]=0 then (row[r]:=1; diag1[r+c]:=1; diag2[r+7-c]:=1; col[c]:=r; try(c+1); row[r]:=0; diag1[r+c]:=0; diag2[r+7-c]:=0) ) in try(0) end let function fact(n : int) : int = if n < 1 then 1 else (n * fact(n - 1)) in fact(10) end /* define valid recursive types */ let /* define a list */ type intlist = {hd: int, tl: intlist} /* define a tree */ type tree ={key: int, children: treelist} type treelist = {hd: tree, tl: treelist} var lis:intlist := intlist { hd=0, tl= nil } in lis end A Language Design Tiger by Andrew Appel, 1996
- 3. Tiger by Andrew Appel, 1996 A Language Design /* A program to solve the 8-queens problem */ let var N := 8 type intArray = array of int var row := intArray [ N ] of 0 var col := intArray [ N ] of 0 var diag1 := intArray [N+N-1] of 0 var diag2 := intArray [N+N-1] of 0 function printboard() = (for i := 0 to N-1 do (for j := 0 to N-1 do print(if col[i]=j then " O" else " ."); print("n")); print("n")) function try(c:int) = ( if c=N then printboard() else for r := 0 to N-1 do if row[r]=0 & diag1[r+c]=0 & diag2[r+7-c]=0 then (row[r]:=1; diag1[r+c]:=1; diag2[r+7-c]:=1; col[c]:=r; try(c+1); row[r]:=0; diag1[r+c]:=0; diag2[r+7-c]:=0) ) in try(0) end let function fact(n : int) : int = if n < 1 then 1 else (n * fact(n - 1)) in fact(10) end /* define valid recursive types */ let /* define a list */ type intlist = {hd: int, tl: intlist} /* define a tree */ type tree ={key: int, children: treelist} type treelist = {hd: tree, tl: treelist} var lis:intlist := intlist { hd=0, tl= nil } in lis end Type Checker Compiler Interpreter Parser
- 4. Tiger by Andrew Appel, 1996 A Language Design /* A program to solve the 8-queens problem */ let var N := 8 type intArray = array of int var row := intArray [ N ] of 0 var col := intArray [ N ] of 0 var diag1 := intArray [N+N-1] of 0 var diag2 := intArray [N+N-1] of 0 function printboard() = (for i := 0 to N-1 do (for j := 0 to N-1 do print(if col[i]=j then " O" else " ."); print("n")); print("n")) function try(c:int) = ( if c=N then printboard() else for r := 0 to N-1 do if row[r]=0 & diag1[r+c]=0 & diag2[r+7-c]=0 then (row[r]:=1; diag1[r+c]:=1; diag2[r+7-c]:=1; col[c]:=r; try(c+1); row[r]:=0; diag1[r+c]:=0; diag2[r+7-c]:=0) ) in try(0) end let function fact(n : int) : int = if n < 1 then 1 else (n * fact(n - 1)) in fact(10) end /* define valid recursive types */ let /* define a list */ type intlist = {hd: int, tl: intlist} /* define a tree */ type tree ={key: int, children: treelist} type treelist = {hd: tree, tl: treelist} var lis:intlist := intlist { hd=0, tl= nil } in lis end Type Checker Compiler Interpreter Parser
- 5. Tiger by Andrew Appel, 1996 A Language Design /* A program to solve the 8-queens problem */ let var N := 8 type intArray = array of int var row := intArray [ N ] of 0 var col := intArray [ N ] of 0 var diag1 := intArray [N+N-1] of 0 var diag2 := intArray [N+N-1] of 0 function printboard() = (for i := 0 to N-1 do (for j := 0 to N-1 do print(if col[i]=j then " O" else " ."); print("n")); print("n")) function try(c:int) = ( if c=N then printboard() else for r := 0 to N-1 do if row[r]=0 & diag1[r+c]=0 & diag2[r+7-c]=0 then (row[r]:=1; diag1[r+c]:=1; diag2[r+7-c]:=1; col[c]:=r; try(c+1); row[r]:=0; diag1[r+c]:=0; diag2[r+7-c]:=0) ) in try(0) end let function fact(n : int) : int = if n < 1 then 1 else (n * fact(n - 1)) in fact(10) end /* define valid recursive types */ let /* define a list */ type intlist = {hd: int, tl: intlist} /* define a tree */ type tree ={key: int, children: treelist} type treelist = {hd: tree, tl: treelist} var lis:intlist := intlist { hd=0, tl= nil } in lis end Type Checker Compiler Interpreter Parser Spoofax {
- 7. Intermediate Language linguistic abstraction | liNGˈgwistik abˈstrakSHən | noun 1. a programming language construct that captures a programming design pattern the linguistic abstraction saved a lot of programming effort he introduced a linguistic abstraction for page navigation in web programming 2. the process of introducing linguistic abstractions linguistic abstraction for name binding removed the algorithmic encoding of name resolution Problem Domain Solution Domain
- 8. “A programming language is low level when its programs require attention to the irrelevant”. -- Alan Perlis, 1982 Problem Domain Solution Domain General- Purpose Language
- 9. Solution Domain Problem Domain Domain-specific language (DSL) noun 1. a programming language that provides notation, analysis, verification, and optimization specialized to an application domain 2. result of linguistic abstraction beyond general-purpose computation General- Purpose Language Domain- Specific Language
- 11. Solution Domain Problem Domain General- Purpose Language Domain- Specific Language Making programming languages is probably very expensive?
- 12. General- Purpose Language Making programming languages is probably very expensive? Solution Domain Problem Domain General- Purpose Language Domain- Specific Language Language Design Compiler + Editor (IDE)
- 13. Compiler + Editor (IDE) Meta-Linguistic Abstraction Language Design General- Purpose Language Declarative Meta Languages Solution Domain Problem Domain General- Purpose Language Domain- Specific Language Language Design
- 15. Language Workbench Language Design Syntax Definition Static Semantics Dynamic Semantics Transforms Meta-DSLs Compiler + Editor (IDE)
- 16. A Language Designer’s Workbench Language Design SDF3 Stratego Consistency Proof NaBL2 DynSem Responsive Editor (IDE) Tests Incremental Compiler Syntax Definition Static Semantics Dynamic Semantics Transforms
- 17. Objective - A workbench supporting design and implementation of programming languages Approach - Declarative multi-purpose domain-specific meta-languages Meta-Languages - Languages for defining languages Domain-Specific - Linguistic abstractions for domain of language definition (syntax, names, types, …) Multi-Purpose - Derivation of interpreters, compilers, rich editors, documentation, and verification from single source Declarative - Focus on what not how; avoid bias to particular purpose in language definition Declarative Language Definition
- 18. Domain Analysis - What are the features of the domain? Language Design - What are adequate linguistic abstractions? - Coverage: can language express everything in the domain? ‣ often the domain is unbounded; language design is making choice what to cover - Minimality: but not more ‣ allowing too much interferes with multi-purpose goal Semantics - What is the semantics of such definitions? - How can we verify the correctness / consistency of language definitions? Implementation - How do we derive efficient language implementations from such definitions? Evaluation - Apply to new and existing languages to determine adequacy Research Methodology
- 19. Representation - Standardized representation for <aspect> of programs - Independent of specific object language Specification Formalism - Language-specific declarative rules - Abstract from implementation concerns Language-Independent Interpretation - Formalism interpreted by language-independent algorithm - Multiple interpretations for different purposes - Reuse between implementations of different languages Separation of Concerns
- 20. Spoofax Language Workbench SDF3: Syntax Definition NaBL2: Static Semantics DynSem: Dynamic Semantics Programming Environment+ +
- 21. Spoofax Language Workbench - ongoing research project aiming to realize a language designer’s workbench SDF3: Syntax definition - context-free grammars + disambiguation + constructors + templates - derivation of parser, formatter, syntax highlighting, … NaBL2: Names & Types - name resolution with scope graphs - type checking/inference with constraints - derivation of name & type resolution algorithm DynSem: Dynamic Semantics - specification of operational (natural) semantics - derivation of interpreter Scopes and Frames - systematic mapping between static names and types and their run-time representation in memory This Lecture
- 22. The Spoofax Language Workbench - Lennart C. L. Kats, Eelco Visser - OOPSLA 2010 A Language Designer's Workbench - A one-stop-shop for implementation and verification of language designs - Eelco Visser, Guido Wachsmuth, Andrew P. Tolmach, Pierre Neron, Vlad A. Vergu, Augusto Passalaqua, Gabriël D. P. Konat - Onward 2014 Literature: Spoofax
- 23. Part I: Syntax
- 24. Pure and declarative syntax definition: paradise lost and regained - Kats, Wachsmuth, Visser - Onward 2010 Literature: Declarative Syntax Definition
- 25. Language = Set of Sentences? fun (x : Int) { x + 1 } Text is a convenient interface for writing and reading programs
- 26. Language = Set of Trees Fun AddArgDecl VarRefId Int “1” VarDeclId “x” TXINT “x” Tree is a convenient interface for transforming programs
- 27. Tree Transformation Add VarRefId VarRefId “y”“x” Mul Int “3” Add VarRefId VarRefId “y”“x” Mul Int “3” Mul Int “3” Add(Mul(Int("3"), VarRefId("x")), Mul(Int("3"), VarRefId("y"))) Mul(Int("3"), Add(VarRefId("x"), VarRefId("y"))) Mul(e1, Add(e2, e3)) -> Add(Mul(e1, e2), Mul(e1, e3))
- 28. Tree Transformation Tree is a convenient interface for transforming programs Semantic transform translate eval analyze refactor type check Syntactic coloring outline view completion
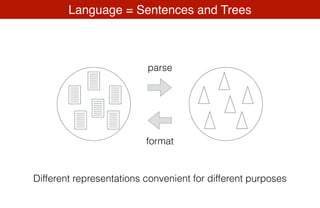
- 29. Language = Sentences and Trees parse format Different representations convenient for different purposes
- 30. From Text to Tree and Back Add VarRefId VarRefId “y”“x” Mul Int “3” Add VarRefId VarRefId “y”“x” Mul Int “3” Mul Int “3” 3 * (x + y) (3 * x) + (3 * y) parse transform format
- 31. Syntax = Tree Structure + Phrase Structure Type Definition.Function ID }( ) {Param* Statement* Statement.If if ( ) elseExp Statement Statement Exp.Add +Exp Exp context-free syntax Definition.Function = < <Type> <ID>(<Param*; separator=",">) { <Statement*; separator="n"> } > Statement.If = < if(<Exp>) <Statement> else <Statement> > Statement.Return = <return <Exp>;> Exp.Add = <<Exp> + <Exp>> Exp.Var = <<ID>> Exp.Var ID Exp Statement.Return return ;
- 32. SDF3 defines Trees and Sentences parse(s) = t where format(t) == s (modulo layout) Expr.Int = INT Expr.Add = <<Expr> + <Expr>> Expr.Mul = <<Expr> * <Expr>> trees (structure) parse (text to tree) format (tree to text) + =>
- 33. Syntax Engineering in Spoofax
- 34. Ambiguity
- 35. Ambiguity t1 != t2 / format(t1) = format(t2) Add VarRef VarRef “y”“x” Mul Int “3” Add VarRef VarRef “y” “x” Mul Int “3” 3 * x + y
- 36. Declarative Disambiguation parse filter Disambiguation Filters [Klint & Visser; 1994], [Van den Brand, Scheerder, Vinju, Visser; CC 2002]
- 37. Priority and Associativity context-free syntax Expr.Int = INT Expr.Add = <<Expr> + <Expr>> {left} Expr.Mul = <<Expr> * <Expr>> {left} context-free priorities Expr.Mul > Expr.Add Recent improvement: safe disambiguation of operator precedence [Afroozeh et al. SLE13, Onward15] Add VarRef VarRef “y”“x” Mul Int “3” Add VarRef VarRef “y” “x” Mul Int “3” 3 * x + y
- 38. Demo: Syntax Definition in the Spoofax Language Workbench
- 39. Representing Incomplete Programs with Placeholders 4 2 3 1 Amorim, Erdweg, Wachsmuth, Visser. Principled syntactic code completion using placeholders. SLE 2016
- 40. Tiger Syntax: Composition module Tiger imports Whitespace imports Types imports Identifiers imports Bindings imports Variables imports Functions imports Numbers imports Strings imports Records imports Arrays imports Control-Flow context-free start-symbols Module context-free syntax Module.Mod = Exp context-free priorities Exp.Or > Exp.Array > Exp.Assign , {Exp.Uminus LValue.FieldVar LValue.Subscript} > {left : Exp.Times Exp.Divide}
- 41. Tiger Syntax: Lexical Syntax module Identifiers lexical syntax Id = [a-zA-Z] [a-zA-Z0-9_]* lexical restrictions Id -/- [a-zA-Z0-9_] lexical syntax Id = "nil" {reject} Id = "let" {reject} Id = … {reject} module Strings sorts StrConst lexical syntax StrConst = """ StrChar* """ StrChar = ~["n] StrChar = [] [n] StrChar = [] [t] StrChar = [] [^] [A-Z] StrChar = [] [0-9] [0-9] [0-9] StrChar = [] ["] StrChar = [] [] StrChar = [] [ tn]+ [] context-free syntax // records Exp.String = StrConst
- 42. Tiger Syntax: Whitespace module Whitespace lexical syntax LAYOUT = [ tnr] CommentChar = [*] LAYOUT = "/*" InsideComment* "*/" InsideComment = ~[*] InsideComment = CommentChar LAYOUT = SingleLineComment SingleLineComment = "//" ~[nr]* NewLineEOF NewLineEOF = [nr] NewLineEOF = EOF EOF = lexical restrictions // Ensure greedy matching for lexicals CommentChar -/- [/] EOF -/- ~[] context-free restrictions // Ensure greedy matching for comments LAYOUT? -/- [ tnr] LAYOUT? -/- [/].[/] LAYOUT? -/- [/].[*]
- 43. Tiger Syntax: Variables and Functions module Bindings imports Control-Flow imports Identifiers imports Types imports Functions imports Variables sorts Declarations context-free syntax Exp.Let = < let <{Dec "n"}*> in <{Exp ";n"}*> end > Declarations.Declarations = < declarations <{Dec "n"}*> > module Variables imports Identifiers imports Types sorts Var context-free syntax Dec.VarDec = <var <Id> : <Type> := <Exp>> Dec.VarDecNoType = <var <Id> := <Exp>> Var.Var = Id LValue = Var Exp = LValue Exp.Assign = <<LValue> := <Exp>> module Functions imports Identifiers imports Types context-free syntax Dec.FunDecs = <<{FunDec "n"}+>> {longest-match} FunDec.ProcDec = < function <Id>(<{FArg ", "}*>) = <Exp> > FunDec.FunDec = < function <Id>(<{FArg ", "}*>) : <Type> = <Exp> > FArg.FArg = <<Id> : <Type>> Exp.Call = <<Id>(<{Exp ", "}*>)>
- 44. Tiger Syntax: Numbers module Numbers lexical syntax IntConst = [0-9]+ lexical syntax RealConst.RealConstNoExp = IntConst "." IntConst RealConst.RealConst = IntConst "." IntConst "e" Sign IntConst Sign = "+" Sign = "-" context-free syntax Exp.Int = IntConst Exp.Uminus = [- [Exp]] Exp.Times = [[Exp] * [Exp]] {left} Exp.Divide = [[Exp] / [Exp]] {left} Exp.Plus = [[Exp] + [Exp]] {left} Exp.Minus = [[Exp] - [Exp]] {left} Exp.Eq = [[Exp] = [Exp]] {non-assoc} Exp.Neq = [[Exp] <> [Exp]] {non-assoc} Exp.Gt = [[Exp] > [Exp]] {non-assoc} Exp.Lt = [[Exp] < [Exp]] {non-assoc} Exp.Geq = [[Exp] >= [Exp]] {non-assoc} Exp.Leq = [[Exp] <= [Exp]] {non-assoc} Exp.And = [[Exp] & [Exp]] {left} Exp.Or = [[Exp] | [Exp]] {left} context-free priorities {Exp.Uminus} > {left : Exp.Times Exp.Divide} > {left : Exp.Plus Exp.Minus} > {non-assoc : Exp.Eq Exp.Neq Exp.Gt Exp.Lt Exp.Geq Exp.Leq} > Exp.And > Exp.Or
- 45. Tiger Syntax: Records, Arrays, Types module Records imports Base imports Identifiers imports Types context-free syntax // records Type.RecordTy = < { <{Field ", n"}*> } > Field.Field = <<Id> : <TypeId>> Exp.NilExp = <nil> Exp.Record = <<TypeId>{ <{InitField ", "}*> }> InitField.InitField = <<Id> = <Exp>> LValue.FieldVar = <<LValue>.<Id>> module Arrays imports Types context-free syntax // arrays Type.ArrayTy = <array of <TypeId>> Exp.Array = <<TypeId>[<Exp>] of <Exp>> LValue.Subscript = <<LValue>[<Index>]> Index = Exp module Types imports Identifiers imports Bindings sorts Type context-free syntax // type declarations Dec.TypeDecs = <<{TypeDec "n"}+>> {longest-match} TypeDec.TypeDec = <type <Id> = <Type>> context-free syntax // type expressions Type = TypeId TypeId.Tid = Id sorts Ty context-free syntax // semantic types Ty.INT = <INT> Ty.STRING = <STRING> Ty.NIL = <NIL> Ty.UNIT = <UNIT> Ty.NAME = <NAME <Id>> Ty.RECORD = <RECORD <Id>> Ty.ARRAY = <ARRAY <Ty> <Id>> Ty.FUN = <FUN ( <{Ty ","}*> ) <Ty>>
- 46. Multi-Purpose Syntax Definition Statement.If = < if(<Exp>) <Statement> else <Statement> > Parser Abstract syntax tree schema Pretty-printer Syntactic completion Folding rules Error recovery Syntactic coloring Outline rules {
- 47. Generating Artifacts from Syntax Definitions Grammar Grammar Normal Form Parse Table Error Recovery Rules Algebraic Signature Program AST Parser Parser Generator Normalizer Language Independent Generator User-Defined Specification Generated Artifact
- 48. Generating Artifacts from Syntax Definitions Grammar Parse Table Algebraic Signature Program AST Parser ParseGen Formatter Generator Formatting Rules Completion Rules AST Completion Generator Language Independent Generator User-Defined Specification Generated Artifact
- 49. Composing Languages - context-free grammars closed under composition - sub-classes of CFG are not closed under composition Generalized Parsing - parsing entire class of context-free grammars ‣ ambiguous grammars ‣ grammars with unbounded lookahead Scannerless Parsing - characters are tokens; no separate scanner Scannerless Generalized LR Parsing - parsing of compositions Composing Syntax Definitions
- 50. Representation: (Abstract Syntax) Trees - Standardized representation for structure of programs - Basis for syntactic and semantic operations Formalism: Syntax Definition - Productions + Constructors + Templates + Disambiguation - Language-specific rules: structure of each language construct Language-Independent Interpretation - Well-formedness of abstract syntax trees ‣ provides declarative correctness criterion for parsing - Parsing algorithm ‣ No need to understand parsing algorithm ‣ Debugging in terms of representation - Formatting based on layout hints in grammar - Syntactic completion Declarative Syntax Definition A meta- language for talking about syntax }
- 51. An Incomplete History of SDF Chomsky Backus, Naur Tomita Heering, Hendriks, Klint, Rekers Rekers Visser Visser van den Brand, Scheerder, Vinju, Visser Bravenboer, Visser Kalleberg Bravenboer, Dolstra, Visser Kats, Visser Erdweg, Rendel, Kästner, Ostermann De Jonge, Kats, Visser, Söderberg Vollebregt, Kats, Visser Erdweg, Rendel, Kästner, Ostermann Amorim, Erdweg, Visser Context-free Grammars BNF Tomita parsing The Syntax Definition Formalism SDF Generalized LR Parsing Character level grammars (SDF2) Scannerless Generalized LR Parsing Disambiguation filters Language embedding SGLR in Java (JSGLR) Preventing injection attacks The Spoofax Language Workbench Library-based syntactic language extensibility (SugarJ) Error recovery for SGLR Template-based grammar productions (SDF3) Layout sensitive generalized parsing Principled Syntactic Code Completion using Placeholders 1956 1963 1985 1988 1992 1995 1997 2002 2004 2006 2010 2010 2011 2012 2012 2012 2016
- 52. Part II: Static Semantics
- 53. Declarative Name Binding and Scope Rules - Konat, Kats, Wachsmuth, Visser - SLE 2012 A Theory of Name Resolution - Néron, Tolmach, Visser, Wachsmuth - ESOP 2015 A constraint language for static semantic analysis based on scope graphs - Van Antwerpen, Néron, Tolmach, Visser, Wachsmuth - PEPM 2016 Literature: NaBL
- 56. Name Binding ?
- 57. let function fact(n : int) : int = if n < 1 then 1 else n * fact(n - 1) in fact(10) end Variables
- 58. let function fact(n : int) : int = if n < 1 then 1 else n * fact(n - 1) in fact(10) end Function Calls
- 59. function prettyprint(tree: tree) : string = let var output := "" function write(s: string) = output := concat(output, s) function show(n: int, t: tree) = let function indent(s: string) = (write("n"); for i := 1 to n do write(" "); output := concat(output, s)) in if t = nil then indent(".") else (indent(t.key); show(n+1, t.left); show(n+1, t.right)) end in show(0, tree); output end Nested Scopes (Shadowing)
- 60. let type point = { x : int, y : int } var origin := point { x = 1, y = 2 } in origin.x := 10; origin := nil end Type References
- 61. let type point = { x : int, y : int } var origin := point { x = 1, y = 2 } in origin.x := 10; origin := nil end Record Fields
- 62. let type point = { x : int, y : int } var origin := point { x = 1, y = 2 } in origin.x := 10; origin := nil end Type Dependent Name Resolution
- 63. name binding ? How to define the rules of a language
- 64. name binding ? What is the BNF of
- 65. Representation - To conduct and represent the results of name resolution Declarative Rules - To define name binding rules of a language Language-Independent Tooling - Name resolution - Code completion - Refactoring - … Separation of Concerns in Name Binding
- 66. Representation - ? Declarative Rules - To define name binding rules of a language Language-Independent Tooling - Name resolution - Code completion - Refactoring - … Separation of Concerns in Name Binding Scope Graphs
- 67. let function fact(n : int) : int = if n < 1 then 1 else n * fact(n - 1) in fact(10) end fact S1 fact S2n n fact nn Scope GraphProgram Name Resolution
- 68. A Calculus for Name Resolution S R1 R2 SR SRS I(R1 ) S’S S’S P Sx Sx R xS xS D Path in scope graph connects reference to declaration Scopes, References, Declarations, Parents, Imports Neron, Tolmach, Visser, Wachsmuth A Theory of Name Resolution ESOP 2015
- 69. Simple Scopes Reference Declaration Scope Reference Step Declaration Step def y1 = x2 + 1 def x1 = 5 S0 def y1 = x2 + 1 def x1 = 5 Sx Sx R xS xS D S0 y1 x1S0 y1 x1S0x2 R y1 x1S0x2 R D y1 x1S0x2 S x x
- 70. Lexical Scoping S1 S0 Parent def x1 = z2 5 def z1 = fun y1 { x2 + y2 } S’S S’S P z1 x1S0z2 S1 y1y2 x2 z1 x1S0z2 S1 y1y2 x2 z1 x1S0z2 S1 y1y2 x2 z1 x1S0z2 R S1 y1y2 x2 z1 x1S0z2 R D S1 y1y2 x2 z1 x1S0z2 R S1 y1y2 x2 z1 x1S0z2 R P S1 y1y2 x2 z1 x1S0z2 R P D S’S Parent Step
- 71. Imports Associated scope Import S0 SB SA module A1 { def z1 = 5 } module B1 { import A2 def x1 = 1 + z2 } A1 SA z1 B1 SB z2 S0 A2 x1 S R1 R2 SR A1 SA z1 B1 SB z2 S0 A2 x1 A1 SA z1 B1 SB z2 S0 A2 x1 A1 SA z1 B1 SB z2 S0 A2 x1 R A1 SA z1 B1 SB z2 S0 A2 x1 R R A1 SA z1 B1 SB z2 S0 A2 x1 R R P A1 SA z1 B1 SB z2 S0 A2 x1 R R P D A1 SA z1 B1 SB z2 S0 A2 x1 I(A2 )R R P D A1 SA z1 B1 SB z2 S0 A2 x1 I(A2 )R R D P D S R1 R2 SR SRS I(R1 ) Import Step
- 72. Qualified Names module N1 { def s1 = 5 } module M1 { def x1 = 1 + N2.s2 } S0 N1 SN s2 S0 N2 R D R I(N2) D X1 s1 N1 SN s2 S0 N2 R D X1 s1 N1 SN s2 S0 N2 X1 s1
- 73. A Calculus for Name Resolution S R1 R2 SR SRS I(R1 ) S’S S’S P Sx Sx R xS xS D Reachability of declarations from references through scope graph edges How about ambiguities? References with multiple paths
- 74. A Calculus for Name Resolution S R1 R2 SR SRS I(R1 ) S’S S’S P Sx Sx R xS xS D I(_).p’ < P.p D < I(_).p’ D < P.p s.p < s.p’ p < p’ Visibility Well formed path: R.P*.I(_)*.D Reachability
- 75. Ambiguous Resolutions match t with | A x | B x => … z1 x2 x1S0x3 z1 x2 x1S0x3 R z1 x2 x1S0x3 R D z1 x2 x1S0x3 R D z1 x2 x1S0x3 R D D S0def x1 = 5 def x2 = 3 def z1 = x3 + 1
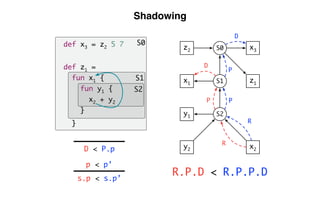
- 76. Shadowing S0 S1 S2 D < P.p s.p < s.p’ p < p’ S1 S2 x1 y1 y2 x2 z1 x3S0z2 def x3 = z2 5 7 def z1 = fun x1 { fun y1 { x2 + y2 } } S1 S2 x1 y1 y2 x2 z1 x3S0z2 R P P D S1 S2 x1 y1 y2 x2 z1 x3S0z2 D P R R P P D R.P.D < R.P.P.D
- 77. Imports shadow Parents I(_).p’ < P.p R.I(A2).D < R.P.D A1 SA z1 B1 SB z2 S0 A2 x1 z3 A1 SA z1 B1 SB z2 S0 A2 x1 I(A2)R D z3 A1 SA z1 B1 SB z2 S0 A2 x1 I(A2)R D P D z3 R S0def z3 = 2 module A1 { def z1 = 5 } module B1 { import A2 def x1 = 1 + z2 } SA SB
- 78. Imports vs. Includes S0def z3 = 2 module A1 { def z1 = 5 } import A2 def x1 = 1 + z2 SA A1 SA z1 z2 S0 A2 x1 I(A2) R D z3 R D D < I(_).p’ R.D < R.I(A2).D A1 SA z1 z2 S0 A2 x1 R z3 D A1 SA z1 z2 S0 A2 x1z3 S0def z3 = 2 module A1 { def z1 = 5 } include A2 def x1 = 1 + z2 SA X
- 79. Import Parents def s1 = 5 module N1 { } def x1 = 1 + N2.s2 S0 SN def s1 = 5 module N1 { } def x1 = 1 + N2.s2 S0 SN Well formed path: R.P*.I(_)*.D N1 SN s2 S0 N2 X1 s1 R I(N2 ) D P N1 SN s2 S0 N2 X1 s1
- 80. Transitive vs. Non-Transitive With transitive imports, a well formed path is R.P*.I(_)*.D With non-transitive imports, a well formed path is R.P*.I(_)?.D A1 SA z1 B1 SB S0 A2 C1 SCz2 x1 B2 A1 SA z1 B1 SB S0 A2 I(A2 ) D C1 SCz2 I(B2 ) R x1 B2 ?? module A1 { def z1 = 5 } module B1 { import A2 } module C1 { import B2 def x1 = 1 + z2 } SA SB SC
- 81. A Calculus for Name Resolution S R1 R2 SR SRS I(R1 ) S’S S’S P Sx Sx R xS xS D I(_).p’ < P.p D < I(_).p’ D < P.p s.p < s.p’ p < p’ Visibility Well formed path: R.P*.I(_)*.D Reachability
- 82. Visibility Policies Lexical scope L := {P} E := P⇤ D < P Non-transitive imports L := {P, I} E := P⇤ · I? D < P, D < I, I < P Transitive imports L := {P, TI} E := P⇤ · TI⇤ D < P, D < TI, TI < P Transitive Includes L := {P, Inc} E := P⇤ · Inc⇤ D < P, Inc < P Transitive includes and imports, and non-transitive imports L := {P, Inc, TI, I} E := P⇤ · (Inc | TI)⇤ · I? D < P, D < TI, TI < P, Inc < P, D < I, I < P, Figure 10. Example reachability and visibility policies by instan- Envre EnvL re EnvD re Envl re
- 84. Let Bindings 1 2 b2a1 c3 a4 b6 c12a10 b11 c5 b9 a7 c8 def a1 = 0 def b2 = 1 def c3 = 2 letpar a4 = c5 b6 = a7 c8 = b9 in a10+b11+c12 1 b2a1 c3 a4 b6 c12a10 b11 c5 b9 a7 c8 2 def a1 = 0 def b2 = 1 def c3 = 2 letrec a4 = c5 b6 = a7 c8 = b9 in a10+b11+c12 1 b2a1 c3 a4 b6 c12a10 b11 c5 b9 a7 c8 2 4 3 def a1 = 0 def b2 = 1 def c3 = 2 let a4 = c5 b6 = a7 c8 = b9 in a10+b11+c12
- 85. Definition before Use / Use before Definition class C1 { int a2 = b3; int b4; void m5 (int a6) { int c7 = a8 + b9; int b10 = b11 + c12; } int c12; } 0 C1 1 2 a2 b4 c12 b3 m5 a6 3 4 c7 b10 b9 a8 b11 c12
- 86. Inheritance class C1 { int f2 = 42; } class D3 extends C4 { int g5 = f6; } class E7 extends D8 { int f9 = g10; int h11 = f12; } 32 1 C4 C1 4D3 E7 D8 f2 g5 f6 f9 g10 f12 h11
- 87. Java Packages package p3; class D4 {} package p1; class C2 {} 1 p3p1 2 p1 p3 3 D4C2
- 88. Java Import package p1; imports r2.*; imports q3.E4; public class C5 {} class D6 {} 4 p1 D6C5 3 2r2 1 p1 E4 q3
- 89. C# Namespaces and Partial Classes namespace N1 { using M2; partial class C3 { int f4; } } namespace N5 { partial class C6 { int m7() { return f8; } } } 1 3 6 4 7 8 C3 C6 N1 N5 f4 m7 N1 N5 C3 C6 f8 2 M2 5
- 90. Representation - To conduct and represent the results of name resolution Declarative Rules - To define name binding rules of a language Language-Independent Tooling - Name resolution - Code completion - Refactoring - … Separation of Concerns in Name Binding
- 91. Representation - ? Declarative Rules - To define name binding rules of a language Language-Independent Tooling - Name resolution - Code completion - Refactoring - … Separation of Concerns in Name Binding Scope Graphs
- 92. Representation - ? Declarative Rules - ? Language-Independent Tooling - Name resolution - Code completion - Refactoring - … Separation of Concerns in Name Binding Scope (& Type) Constraint Rules [PEPM16] Scope Graphs
- 94. Scope Graph Constraints new s // new scope s1 -L-> s2 // labeled edge from scope s1 to scope s2 N{x} <- s // x is a declaration in scope s for namespace N N{x} -> s // x is a reference in scope s for namespace N N{x} |-> d // x resolves to declaration d [[ e ^ (s) ]] // constraints for expression e in scope s
- 95. let var x : int := x + 1 in x + 1 end s s_bodyx x Let( [VarDec( "x" , Tid("int") , Plus(Var("x"), Int("1")) )] , [Plus(Var("x"), Int("1"))] ) [[ Let([VarDec(x, t, e)], [e_body]) ^ (s) ]] := new s_body, // new scope s_body -P-> s, // parent edge to enclosing scope Var{x} <- s_body, // x is a declaration in s_body [[ e ^ (s) ]], // init expression [[ e_body ^ (s_body) ]]. // body expression [[ Var(x) ^ (s') ]] := Var{x} -> s', // x is a reference in s' Var{x} |-> d, // check that x resolves to a declaration s’ x ? P
- 96. How about types?
- 97. Type Constraints d : ty // declaration has type t1 == ty2 // type equality ty1 <! ty2 // declare sub-type ty1 <? ty2 // query sub-type . . . // extensions [[ e ^ (s) : ty ]] // type of expression in scope
- 98. s s_bodyx x [[ Let([VarDec(x, t, e)], [e_body]) ^ (s) : ty' ]] := new s_body, // new scope s_body -P-> s, // parent edge to enclosing scope Var{x} <- s_body, // x is a declaration in s_body Var{x} : ty, // associate type [[ t ^ (s) : ty ]], // type of type [[ e ^ (s) : ty ]], // type of expression [[ e_body ^ (s_body) : ty' ]]. // constraints for body [[ Var(x) ^ (s') : ty ]] := Var{x} -> s', // x is a reference in s' Var{x} |-> d, // check that x resolves to a declaration d : ty. // type of declaration is type of reference s’ x let var x : int := x + 1 in x + 1 end Let( [VarDec( "x" , Tid("int") , Plus(Var("x"), Int("1")) )] , [Plus(Var("x"), Int("1"))] ) INT
- 99. let type point = {x : int, y : int} var origin : point := … in origin.x end S2 S3 x x point [[ FieldVar(e, f) ^ (s) : ty ]] := [[ e ^ (s) : ty_e ]], new s_use, Field{f} -> s_use, s_use -I-> s_rec, ty_e == RECORD(s_rec), Field{f} |-> d, d : ty. [[ RecordTy(fields) ^ (s) : ty ]] := ty == RECORD(s_rec), new s_rec, Map2[[ fields ^ (s_rec, s) ]]. [[ Field(x, t) ^ (s_rec, s_outer) ]] := Field{x} <- s_rec, Field{x} : ty !, [[ t ^ (s_outer) : ty ]]. S1 point s_rec y RECORD INT origin origin s_use s_recty_e Type Dependent Name Resolution
- 100. Tiger Names & Types: Composition module statics/tiger imports statics/arrays imports statics/base imports statics/bindings imports statics/control-flow imports statics/functions imports statics/nabl-lib imports statics/numbers imports statics/records imports statics/strings imports statics/types imports statics/variables rules // top-level module [[ Mod(e) ^ (s) : ty ]] := [[ e ^ (s) : ty ]].
- 101. Tiger Names & Types: Composition module statics/functions imports signatures/Functions-sig imports statics/nabl-lib imports statics/base rules // function declarations Dec[[ FunDecs(fdecs) ^ (s, s_outer) ]] := Map2[[ fdecs ^ (s, s_outer) ]]. [[ FunDec(f, args, t, e) ^ (s, s_outer) ]] := new s_fun, s_fun -P-> s, distinct/name D(s_fun) | error $[duplicate argument] @ NAMES, MapTs2[[ args ^ (s_fun, s_outer) : tys ]], [[ t ^ (s_outer) : ty ]], Var{f} <- s, Var{f} : FUN(tys, ty) !, [[ e ^ (s_fun) : ty_body ]], ty == ty_body| error $[return type does not match body] @ t. [[ FArg(x, t) ^ (s_fun, s_outer) : ty ]] := Var{x} <- s_fun, Var{x} : ty !, [[ t ^ (s_outer) : ty ]]. rules // function calls [[ Call(f, exps) ^ (s) : ty ]] := Var{f} -> s, Var{f} |-> d | error $[Function [f] not declared], d : FUN(tys, ty) | error $[Function expected] , MapSTs[[ exps ^ (s) : tys ]].
- 102. Tiger Names & Types: Composition module statics/bindings imports signatures/Bindings-sig imports statics/nabl-lib imports statics/base imports statics/control-flow imports statics/variables rules // let [[ Let(blocks, exps) ^ (s) : ty ]] := new s_body, Decs[[ blocks ^ (s, s_body) ]], Seq[[ exps ^ (s_body) : ty ]], distinct D(s_body). Decs[[ [] ^ (s_outer, s_body) ]] := s_body -P-> s_outer. Decs[[ [block] ^ (s_outer, s_body) ]] := s_body -P-> s_outer, Dec[[ block ^ (s_body, s_outer) ]]. Decs[[ [block | blocks@[_|_]] ^ (s_outer, s_body) ]] := new s_dec, s_dec -P-> s_outer, Dec[[ block ^ (s_dec, s_outer) ]], Decs[[ blocks ^ (s_dec, s_body) ]], distinct/name D(s_dec) | error $[duplicate declaration] @NAMES. // Nested scopes: The scope of a variable or parameter includes the // bodies of any function definitions in that scope. That is, access // to variables in outer scopes is permitted, as in Pascal and Algol /* Local redeclarations: A variable or function declaration may be hidden by the redeclaration of the same name (as a variable or function) in a smaller scope; for example, this function prints "6 7 6 8 6" when applied to 5: let function f(v : int) = let var v := 6 in print(v); let var v := 7 in print(v) end; print(v); let var v := 8 in print(v) end; print(v) end in f(4) end */
- 103. Tiger Names & Types: Variables module statics/variables imports signatures/Variables-sig imports statics/nabl-lib imports statics/base rules // variable declarations Dec[[ VarDec(x, t, e) ^ (s, s_outer) ]] := [[ t ^ (s_outer) : ty1 ]], [[ e ^ (s_outer) : ty2 ]], ty2 <? ty1 | error $[type mismatch got [ty2] where [ty1] expected] @ e, Var{x} <- s, Var{x} : ty1 !. Dec[[ VarDecNoType(x, e) ^ (s, s_outer) ]] := [[ e ^ (s_outer) : ty ]], ty != NIL() | error $[explicit type expected for variable initialized with nil], Var{x} <- s, Var{x} : ty !. rules // variable references [[ Var(x) ^ (s) : ty ]] := Var{x} -> s, // declare x as variable reference Var{x} |-> d, // check that x resolves to a declaration d : ty. // type of declaration is type of reference rules // statements [[ Assign(e1, e2) ^ (s) : UNIT() ]] := [[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s) : ty2 ]], ty2 <? ty1 | error $[type mismatch got [ty2] where [ty1] expected] @ e2.
- 104. Tiger Names & Types: Records (1) module statics/records imports signatures/Records-sig imports statics/nabl-lib imports statics/base rules // record type [[ RecordTy(fields) ^ (s) : ty ]] := new s_rec, ty == RECORD(s_rec), NIL() <! ty, distinct/name D(s_rec)/Field | error $[Duplicate declaration of field [NAME]] @ NAMES, Map2[[ fields ^ (s_rec, s) ]]. [[ Field(x, t) ^ (s_rec, s_outer) ]] := Field{x} <- s_rec, Field{x} : ty !, [[ t ^ (s_outer) : ty ]].
- 105. Tiger Names & Types: Records (2) module statics/records … rules // record creation [[ r@Record(t, inits) ^ (s) : ty ]] := [[ t ^ (s) : ty ]], ty == RECORD(s_rec) | error $[record type expected], new s_use, s_use -I-> s_rec, D(s_rec)/Field subseteq/name R(s_use)/Field | error $[Field [NAME] not initialized] @r, distinct/name R(s_use)/Field | error $[Duplicate initialization of field [NAME]] @NAMES, Map2[[ inits ^ (s_use, s) ]]. [[ InitField(x, e) ^ (s_use, s) ]] := Field{x} -> s_use, Field{x} |-> d, d : ty1, [[ e ^ (s) : ty2 ]], ty2 <? ty1 | error $[type mismatch got [ty2] where [ty1] expected]. rules // record field access [[ FieldVar(e, f) ^ (s) : ty ]] := [[ e ^ (s) : ty_e ]], ty_e == RECORD(s_rec), new s_use, s_use -I-> s_rec, Field{f} -> s_use, Field{f} |-> d, d : ty.
- 106. Tiger Names & Types: Records (2) module statics/arrays imports signatures/Arrays-sig imports statics/nabl-lib imports statics/base rules // array type [[ ArrayTy(t) ^ (s) : ARRAY(ty, s')]] := new s', // unique token to distinghuish the array type [[ t ^ (s) : ty ]]. rules // array creation [[ Array(t, e1, e2) ^ (s) : ty ]] := [[ t ^ (s) : ty ]], ty == ARRAY(ty_elem, s_arr) | error $[array type expected], ty_elem2 <? ty_elem | error $[type mismatch [ty_indic] expected] @ e2, [[ e1 ^ (s) : INT() ]], // length [[ e2 ^ (s) : ty_elem2 ]]. // initial value rules // array indexing [[ Subscript(e1, e2) ^ (s) : ty ]] := [[ e1 ^ (s) : ty_arr ]], ty_arr == ARRAY(ty, s_arr), [[ e2 ^ (s) : INT() ]].
- 107. Tiger Names & Types: Numbers module statics/numbers imports signatures/Numbers-sig imports statics/nabl-lib imports statics/base rules // literals [[ Int(i) ^ (s) : INT() ]]. rules // operators [[ Uminus(e) ^ (s) : INT() ]] := [[ e ^ (s) : INT() ]]. [[ Divide(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : INT() ]], [[ e2 ^ (s): INT() ]]. [[ Times(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : INT() ]], [[ e2 ^ (s): INT() ]]. [[ Minus(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : INT() ]], [[ e2 ^ (s): INT() ]]. [[ Plus(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : INT() ]], [[ e2 ^ (s): INT() ]]. [[ Eq(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]], ty1 == ty2. [[ Neq(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]], ty1 == ty2. [[ Gt(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]], ty1 == ty2. [[ Lt(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]], ty1 == ty2. [[ Geq(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]], ty1 == ty2. [[ Leq(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]], ty1 == ty2. [[ Or(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]], ty1 == ty2. [[ And(e1, e2) ^ (s) : INT() ]] := [[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]], ty1 == ty2.
- 108. Tiger Names & Types: Numbers module statics/control-flow imports signatures/Control-Flow-sig imports statics/nabl-lib imports statics/base rules // sequence Seq[[ [] ^ (s) : UNIT() ]]. Seq[[ [e] ^ (s) : ty ]] := [[ e ^ (s) : ty ]]. Seq[[ [ e | es@[_|_] ] ^ (s) : ty ]] := [[ e ^ (s) : ty' ]], Seq[[ es ^ (s) : ty ]]. [[ Seq(es) ^ (s) : ty ]] := Seq[[ es ^ (s) : ty ]]. [[ If(e1, e2, e3) ^ (s) : ty2 ]] := [[ e1 ^ (s) : INT() ]], [[ e2 ^ (s) : ty2 ]], [[ e3 ^ (s) : ty3 ]], ty2 == ty3 | error $[branches should have same type]. [[ IfThen(e1, e2) ^ (s) : UNIT() ]] := [[ e1 ^ (s) : INT() ]], [[ e2 ^ (s) : UNIT() ]]. [[ While(e1, e2) ^ (s) : UNIT() ]] := new s', s' -P-> s, Loop{""} <- s', [[ e1 ^ (s) : INT() ]], [[ e2 ^ (s') : UNIT() ]]. [[ stm@For(Var(x), e1, e2, e3) ^ (s) : UNIT() ]] := new s_for, s_for -P-> s, Var{x} <- s_for, Var{x} : INT(), Loop{Break()@stm} <- s_for, [[ e1 ^ (s) : INT() ]], // x not bound in loop bounds [[ e2 ^ (s) : INT() ]], [[ e3 ^ (s_for) : UNIT() ]]. // x bound in body [[ stm@Break() ^ (s) : UNIT() ]] := Loop{Break()@stm} -> s, Loop{Break()@stm} |-> d.
- 109. Representation - ? Declarative Rules - ? Language-Independent Tooling - Name resolution - Code completion - Refactoring - … Separation of Concerns in Name Binding Scope Graphs Scope & Type Constraint Rules A language for talking about name binding}
- 110. NaBL2 in Spoofax Language Workbench http://spoofax.org
- 111. Domain-Specific Languages - Ice Dust2 [ECOOP17] - Green-Marl (Oracle) Education - Mini-Java, Tiger, Calc Programming languages - Pascal, TypeScript, F# - (student projects in progress) Bootstrapping language workbench - NaBL2, … Applications
- 112. Scopes Describe Frames [ECOOP16] S x y l’l : T : T S’ S’’ xx S y l l’ x S’ x S’’ A Uniform Model for Memory Layout in Dynamic Semantics
- 113. Theory - Resolution calculus - Name binding and type constraints - Resolution algorithm sound wrt calculus - Mapping to run-time memory layout Declarative specification - NaBL2: generation of name and type constraints Tooling - Solver (second version) - Integrated in Spoofax Language Workbench ‣ editors with name and type checking ‣ navigation Scope Graphs for Name Binding: Status
- 114. A domain-specific (= restricted) model - cannot describe all name resolution algorithms implemented in Turing complete languages Normative model - ‘this is name binding’ Claim/hypothesis - Describes all sane models of name binding Scope Graphs for Name Binding: Limitations
- 115. Theory - Scopes = structural types? ‣ operations for scope / type comparison - Generics ‣ DOT-style? - Type soundness of interpreters — automatically Tooling - Tune name binding language (notation) - Incremental analysis (in progress) - Code completion - Refactoring (renaming) Scope Graphs for Name Binding: Future Work
- 116. A common (cross-language) understanding of name binding? A foundation for formalization and implementation of programming languages? Scope Graphs for Name Binding: The Future A1 SA z1 B1 SB z2 S0 A2 x1 A1 SA z1 B1 SB z2 S0 A2 x1 A1 SA z1 B1 SB z2 S0 A2 x1 A1 SA z1 B1 SB z2 S0 A2 x1 R A1 SA z1 B1 SB z2 S0 A2 x1 R R A1 SA z1 B1 SB z2 S0 A2 x1 R R P A1 SA z1 B1 SB z2 S0 A2 x1 R R P D A1 SA z1 B1 SB z2 S0 A2 x1 I(A2 )R R P D A1 SA z1 B1 SB z2 S0 A2 x1 I(A2 )R R D P D
- 118. DynSem: A DSL for Dynamic Semantics Specification - Vergu, Néron, Visser - RTA 2015 Literature: DynSem
- 120. What is the meaning of a program? meaning(p) = what happens when executing the generated (byte) code to which p is compiled source code parse generate machine code check meaning(p) = behavior(p)
- 121. What is the meaning of a program? Mapping input to output What is behavior? Changes to state of the system How can we observe behavior? Which behavior is essential, which accidental? meaning(p) = behavior(p)
- 122. How can we define the semantics of a program? Is there a more direct description of semanticsL1? Compiler defines translational semantics semanticsL1(p) = semanticsL2(translate(p)) Requires understanding translate and semanticsL2 How do we know that translate is correct?
- 123. Operational Semantics What is the result of execution of a program and how is that result achieved? Natural Semantics: How is overall result of execution obtained? Structural Operational Semantics: What are the individual steps of an execution? Defined using a transition system
- 124. Transition System e1 ➞ e1’ … en ➞ en’ e ➞ e’ conclusion premises rule e ➞ e’axiom reduction p ➞ v
- 125. Structural Operational (Small-Step) Semantics e1 ➞ e1’ ifz(e1) e2 else e3 ➞ ifz(e1’) e2 else e3 i != 0 ifz(i) e2 else e3 ➞ e3 ifz(0) e2 else e3 ➞ e2 (x.e) v1 ➞ e[x := v1] e1 ➞ e1’ e1 e2 ➞ e1’ e2 e2 ➞ e2’ v e2 ➞ v e2’ e1 ➞ e1’ e1 + e2 ➞ e1’ + e2 e2 ➞ e2’ e1 + e2 ➞ e1 + e2’ i + j ➞ i + j e ➞ e reducing expressions e = x | i | e + e | x.e | e e | ifz(e) e else e order of evaluation?
- 126. Natural (Big-Step) Semantics E ⊢ e1 NumV(i) E ⊢ e2 NumV(j) E ⊢ e1 + e2 NumV(i + j) E[x] = v E ⊢ x v E ⊢ x.e ClosV(x, e, E) E ⊢ i NumV(i) E ⊢ e1 NumV(0) E ⊢ e2 v E ⊢ if(e1) e2 else e3 v E ⊢ e1 NumV(i), i != 0 E ⊢ e3 v E ⊢ if(e1) e2 else e3 v E1 ⊢ e1 ClosV(x, e, E2) E1 ⊢ e2 v1 {x ↦ v1, E2} ⊢ e v2 E1 ⊢ e1 e2 v2 E ⊢ e v reducing expressions to values e = x | i | e + e | x.e | e e | ifz(e) e else e
- 127. DynSem: A DSL for Dynamic Semantics Specification Concise ModularExecutable PortableDesign Goals M. Churchill, P. D. Mosses, and P. Torrini. Reusable components of semantic specifications. In MODULARITY, April 2014. High-performance Statically Typed Big-Step I-MSOS Unsurprising Vlad Vergu, Pierre Neron, Eelco Visser. DynSem: A DSL for Dynamic Semantics Specification. RTA 2015
- 128. Example: DynSem Semantics of PAPL-Box let fac = box(0) in let f = fun (n) { if (n == 0) 1 else n * (unbox(fac) (n - 1)) end } in setbox(fac, f); unbox(fac)(10) end end Features - Arithmetic - Booleans - Comparisons - Mutable variables - Functions - Boxes Components - Syntax in SDF3 - Dynamic Semantics in DynSem
- 129. Abstract Syntax from Concrete Syntax module Arithmetic imports Expressions imports Common context-free syntax Expr.Num = INT Expr.Plus = [[Expr] + [Expr]] {left} Expr.Minus = [[Expr] - [Expr]] {left} Expr.Times = [[Expr] * [Expr]] {left} Expr.Mod = [[Expr] % [Expr]] {left} context-free priorities {left: Expr.Times Expr.Mod } > {left: Expr.Minus Expr.Plus } module Arithmetic-sig imports Expressions-sig imports Common-sig signature sorts Expr constructors Num : INT -> Expr Plus : Expr * Expr -> Expr Minus : Expr * Expr -> Expr Times : Expr * Expr -> Expr Mod : Expr * Expr -> Expr src-gen/ds-signatures/Arithmetic-sig
- 130. Values, Meta-Variables, and Arrows module expressions imports values imports Expressions-sig signature arrows Expr --> V variables e : Expr x : String module values signature sorts V Unit constructors U : Unit variables v: V
- 131. Term Reduction Rules module arithmetic-explicit imports expressions primitives Arithmetic-sig signature constructors NumV: Int -> V rules Num(__String2INT__(n)) --> NumV(str2int(n)). Plus(e1, e2) --> NumV(plusI(i1, i2)) where e1 --> NumV(i1); e2 --> NumV(i2). Minus(e1, e2) --> NumV(minusI(i1, i2)) where e1 --> NumV(i1); e2 --> NumV(i2). module primitives signature native operators str2int : String -> Int plusI : Int * Int -> Int minusI : Int * Int -> Int
- 132. Native Operations module primitives signature native operators str2int : String -> Int plusI : Int * Int -> Int minusI : Int * Int -> Int public class Natives { public static int plusI_2(int i1, int i2) { return i1 + i2; } public static int str2int_1(String s) { return Integer.parseInt(s); } }
- 133. Arrows as Coercions rules Plus(e1, e2) --> NumV(plusI(i1, i2)) where e1 --> NumV(i1); e2 --> NumV(i2). rules Plus(NumV(i1), NumV(i2)) --> NumV(plusI(i1, i2)). signature constructors Plus : Expr * Expr -> Expr NumV : Int -> V arrows Expr --> V
- 134. Modular module boolean imports Booleans-sig expressions signature constructors BoolV : Bool -> V rules True() --> BoolV(true). False() --> BoolV(false). Not(BoolV(false)) --> BoolV(true). Not(BoolV(true)) --> BoolV(false). Or(BoolV(true), _) --> BoolV(true). Or(BoolV(false), e) --> e. And(BoolV(false), _) --> BoolV(false). And(BoolV(true), e) --> e. module comparison imports Comparisons-sig arithmetic boolean rules Gt(NumV(i1), NumV(i2)) --> BoolV(gtI(i1, i2)). Eq(NumV(i1), NumV(i2)) --> BoolV(eqI(i1, i2)). Eq(BoolV(b1), BoolV(b2)) --> BoolV(eqB(b1, b2)). module arithmetic imports Arithmetic-sig imports expressions imports primitives signature constructors NumV: Int -> V rules Num(str) --> NumV(str2int(str)). Plus(NumV(i1), NumV(i2)) --> NumV(plusI(i1, i2)). Minus(NumV(i1), NumV(i2)) --> NumV(minusI(i1, i2)). Times(NumV(i1), NumV(i2)) --> NumV(timesI(i1, i2)). Mod(NumV(i1), NumV(i2)) --> NumV(modI(i1, i2)).
- 135. Control-Flow module controlflow imports ControlFlow-sig imports expressions imports boolean rules Seq(v, e2) --> e2. If(BoolV(true), e1, _) --> e1. If(BoolV(false), _, e2) --> e2. module controlflow imports ControlFlow-sig imports expressions imports boolean rules Seq(e1, e2) --> v2 where e1 --> v1; e2 --> v2. If(e1, e2, e3) --> v where e1 --> BoolV(true); e2 --> v. If(e1, e2, e3) --> v where e1 --> BoolV(false); e3 --> v.
- 136. Immutable Variables: Environment Passing module variables imports Variables-sig environment rules E |- Let(x, v: V, e2) --> v2 where Env {x |--> v, E} |- e2 --> v2. E |- Var(x) --> E[x]. constructors Fun : ID * Expr -> Expr App : Expr * Expr -> Expr module environment imports values signature sort aliases Env = Map<String, V> variables E : Env
- 137. First-Class Functions: Environment in Closure module unary-functions imports expressions environment signature constructors ClosV : String * Expr * Env -> V rules E |- Fun(x, e) --> ClosV(x, e, E). E |- App(e1, e2) --> v where E |- e1 --> ClosV(x, e, E'); E |- e2 --> v2; Env {x |--> v2, E'} |- e --> v. constructors Fun : ID * Expr -> Expr App : Expr * Expr -> Expr module environment imports values signature sort aliases Env = Map<String, V> variables E : Env module variables imports Variables-sig environment rules E |- Let(x, v: V, e2) --> v2 where Env {x |--> v, E} |- e2 --> v2. E |- Var(x) --> E[x].
- 138. Implicit Propagation rules E |- Plus(e1, e2) --> NumV(plusI(i1, i2)) where E |- e1 --> NumV(i1); E |- e2 --> NumV(i2). rules Plus(e1, e2) --> NumV(plusI(i1, i2)) where e1 --> NumV(i1); e2 --> NumV(i2). rules Plus(NumV(i1), NumV(i2)) --> NumV(plusI(i1, i2)).
- 139. Mutable Boxes: Store module box imports store arithmetic signature constructors Box : Expr -> Expr Unbox : Expr -> Expr SetBox : Expr * Expr -> Expr constructors BoxV: Int -> V rules Box(e) :: S --> BoxV(loc) :: Store {loc |--> v, S'} where e :: S --> v :: S'; fresh => loc. Unbox(BoxV(loc)) :: S --> S[loc]. SetBox(BoxV(loc), v) :: S --> v :: Store {loc |--> v, S}. module store imports values signature sort aliases Store = Map<Int, V> variables S : Store
- 140. Mutable Variables: Environment + Store constructors Let : ID * Expr * Expr -> Expr Var : ID -> Expr Set : String * Expr -> Expr module variables-mutable imports Variables-sig store rules E |- Var(x) :: S --> v :: S where E[x] => loc; S[loc] => v. E |- Let(x, v, e2) :: S1 --> v2 :: S3 where fresh => loc; {loc |--> v, S1} => S2; Env {x |--> loc, E} |- e2 :: S2 --> v2 :: S3. E |- Set(x, v) :: S --> v :: Store {loc |--> v, S} where E[x] => loc. module store imports values signature sort aliases Env = Map<ID, Int> Store = Map<Int, V> variables E : Env S : Store
- 141. Implicit Store Threading rules E |- Plus(e1, e2) :: S1 --> NumV(plusI(i1, i2)) :: S3 where E |- e1 :: S1 --> NumV(i1) :: S2; E |- e2 :: S2 --> NumV(i2) :: S3. rules Plus(e1, e2) --> NumV(plusI(i1, i2)) where e1 --> NumV(i1); e2 --> NumV(i2). rules Plus(NumV(i1), NumV(i2)) --> NumV(plusI(i1, i2)).
- 142. Abstraction: Env/Store Meta Functions module store imports values signature sort aliases Env = Map<String, Int> Store = Map<Int, V> variables E : Env S : Store constructors readVar : String --> V bindVar : String * V --> Env writeVar : String * V --> V allocate : V --> Int write : Int * V --> V read : Int --> V rules allocate(v) --> loc where fresh => loc; write(loc, v) --> _. write(loc, v) :: S --> v :: Store {loc |--> v, S}. read(loc) :: S --> S[loc] :: S. rules bindVar(x, v) --> {x |--> loc} where allocate(v) --> loc. E |- readVar(x) --> read(E[x]). E |- writeVar(x, v) --> write(E[x], v).
- 143. Boxes with Env/Store Meta Functions module boxes signature constructors Box : Expr -> Expr Unbox : Expr -> Expr SetBox : Expr * Expr -> Expr constructors BoxV: V -> V rules Box(v) --> BoxV(NumV(allocate(v))). Unbox(BoxV(NumV(loc))) --> read(loc). SetBox(BoxV(NumV(loc)), v) --> write(loc, v).
- 144. Mutable Variables with Env/Store Meta Functions module variables imports expressions store rules Var(x) --> readVar(x). E |- Let(x, v1, e) --> v2 where bindVar(x, v1) --> E'; Env {E', E} |- e --> v2. Set(x, v) --> v where writeVar(x, v) --> _. constructors Let : String * Expr * Expr -> Expr Var : String -> Expr Set : String * Expr -> Expr
- 145. Functions with Multiple Arguments module functions imports Functions-sig imports variables signature constructors ClosV : List(ID) * Expr * Env -> V bindArgs : List(ID) * List(Expr) --> Env rules E |- Fun(xs, e) --> ClosV(xs, e, E). App(ClosV(xs, e_body, E_clos), es) --> v' where bindArgs(xs, es) --> E_params; Env {E_params, E_clos} |- e_body --> v'. bindArgs([], []) --> {}. bindArgs([x | xs], [e | es]) --> {E, E'} where bindVar(x, e) --> E; bindArgs(xs, es) --> E'.
- 147. Tiger in DynSem
- 148. DynSem Meta-Interpreter Tiger Program Tiger AST Tiger in DynSem Rules Value DynSem Meta Interpreter Truffle/Graal Can Truffle specialize through two levels of interpretation?
- 149. Complete - Tiger - Simpl - PaplBox - Calc - … Under Construction - Grace - Lambda_JS - … Applications of DynSem
- 150. Part IV: Scopes & Frames
- 151. Scopes Describe Frames: A Uniform Model for Memory Layout in Dynamic Semantics - Bach Poulsen, Néron, Tolmach, Visser. - ECOOP 2016 Literature: Scopes & Frames
- 152. Consistency of Language Definitions Type soundness Semantics preservation Soundness and completeness of type inference Automate the verification of consistency properties
- 153. Example: Encoding Units compiler computerinput input distance : Float; input duration : Float; output speed : Float := duration / distance; error wrong output
- 154. Impact of Software Errors compiler computer error Mars Climate Orbiter Unit mismatch: Orbiter variables in Newtons, Ground control software in Pound-force. Damage: ~350 M$ input distance : Float; input duration : Float; output speed : Float := duration / distance; wrong output
- 155. Example: Explicit Representation of Units computer input distance : Meter; input duration : Second; output speed : Meter/Second := duration / distance; compiler formalize knowledge of application area (domain) in language error
- 156. Problem: Correctness of Language Definitions error computer compiler Can we trust the compiler? wrong outputinput program type soundness: well-typed programs don’t go wrong
- 157. Challenge: Automatic Verification of Correctness compiler error computer compiler wrong output program type soundness: well-typed programs don’t go wrong type checker code generator input
- 158. Semantic Specification Tools IDEs Type Checkers Language Run Time Garbage Collector Static Semantics Dynamic Semantics Binding Binding Garbage Collector✔ Proof Assistant Infrastructure Type Soundness
- 159. Static Dynamic Lexical val x = 31; val y = x + 11; Typing Contexts Type Substitution Substitution Environments De Bruijn Indices HOAS Mutable var x = 31; x = x + 11; Typing Contexts Store Typing Stores/Heaps Objects class A { var x = 0; var y = 42; } var r = new A(); Class Tables Mutable Objects Stores/Heaps
- 160. S x y l’l S’ S’’ xx S y l l’ x S’ x S’’ Scope Frame [ESOP’15] [ECOOP’16]
- 161. 1 x1 2 x yx 1 2 x yx R 1 2 x yx R P 1 2 x yx R P D P scope declaration reference scope edgel val x = 31; val y = x + 11; Lexical Scoping [ESOP’15; PEPM’16]
- 162. class A { var x = 42; } class B extends A { var y = x; } scope declaration reference scope edgel associated scope 1 A B 2 3 I x y x 1 A B 2 3 I x y x Inheritance
- 163. More Binding Patterns Shadowing S0 S1 S2 D < P.p s.p < s.p’ p < p’ S1 S2 x1 y1 y2 x2 z1 x3S0z2 def x3 = z2 5 7 def z1 = fun x1 { fun y1 { x2 + y2 } } S1 S2 x1 y1 y2 x2 z1 x3S0z2 R P P D S1 S2 x1 y1 y2 x2 z1 x3S0z2 D P R R P P D R.P.D < R.P.P.D Java Import package p1; imports r2.*; imports q3.E4; public class C5 {} class D6 {} 4 p1 D6C5 3 2r2 1 p1 E4 q3 Java Packages package p3; class D4 {} package p1; class C2 {} 1 p3p1 2 p1 p3 3 D4C2 C# Namespaces and Partial Classes namespace N1 { using M2; partial class C3 { int f4; } } namespace N5 { partial class C6 { int m7() { return f8; } } } 1 3 6 4 7 8 C3 C6 N1 N5 f4 m7 N1 N5 C3 C6 f8 2 M2 5 Transitive vs. Non-Transitive With transitive imports, a well formed path is R.P*.I(_)*.D With non-transitive imports, a well formed path is R.P*.I(_)? .D A1 SA z1 B1 SB S0 A2 C1 SCz2 x1 B2 A1 SA z1 B1 SB S0 A2 I(A2 ) D C1 SCz2 I(B2 ) R x1 B2 ?? module A1 { def z1 = 5 } module B1 { import A2 } module C1 { import B2 def x1 = 1 + z2 } SA SB SC [ESOP’15] Qualified Names module N1 { def s1 = 5 } module M1 { def x1 = 1 + N2.s2 } S0 N1 SN s2 S0 N2 R D R I(N2) D X1 s1 N1 SN s2 S0 N2 R D X1 s1 N1 SN s2 S0 N2 X1 s1
- 164. Static Dynamic Lexical val x = 31; val y = x + 11; Typing Contexts Type Substitution Substitution Environments De Bruijn Indices HOAS Mutable var x = 31; x = x + 11; Typing Contexts Store Typing Stores/Heaps Objects class A { var x = 0; var y = 42; } var r = new A(); Class Tables Mutable Objects Stores/Heaps
- 165. Static Dynamic Lexical val x = 31; val y = x + 11; Substitution Environments De Bruijn Indices HOAS Mutable var x = 31; x = x + 11; Stores/Heaps Objects class A { var x = 0; var y = 42; } var r = new A(); Mutable Objects Stores/Heaps 1 2 x yx R P D 1 x x x 1 A 2 x A y r
- 166. S x y l’l S’ S’’ xx S y l l’ x S’ x S’’ Scope Frame [ECOOP’16] Slots Links
- 167. 1 2 x yx R P D val x = 31; val y = x + 11; P x x 1 x x 31 1 x x 31 1 x y 2 P x x 31 x 1 x y 2 P x x 31 1 x y 42 2 P
- 168. def fac(n : Int) : Int = { if (n == 0) 1 else n * fac(n - 1) }; fac(2); x fac 1 x fac Fn 1 x fac Fn 1 fac x fac Fn 1 x n 2 P x fac Fn 1 x n 2 2 P x fac Fn 1 x n 2 2 n facnn P x fac Fn 1 x n 2 2 x n 2 PP x fac Fn 1 x n 2 2 x n 1 2 PP x fac Fn 1 x n 2 2 x n 1 2 n facnn PP x fac Fn 1 x n 2 2 x n 1 2 x n 0 2 P PP x fac Fn 1 x n 2 2 x n 1 2 x n 0 2 P n PP x 1 2 fac n xn fac fac P
- 169. class A { var x = 0; var y = 42; } var r = new A(); xA 1 r xA 1 r xx 0 2 y 42 1 A 2 x A y r
- 170. Static Dynamic Lexical val x = 31; val y = x + 11; Substitution Environments De Bruijn Indices HOAS Mutable var x = 31; x = x + 11; Stores/Heaps Objects class A { var x = 0; var y = 42; } var r = new A(); Mutable Objects Stores/Heaps 1 2 x yx R P D 1 x x x 1 A 2 x A y r
- 171. Static Dynamic Lexical val x = 31; val y = x + 11; Mutable var x = 31; x = x + 11; Objects class A { var x = 0; var y = 42; } var r = new A(); 1 2 x yx R P D x x 31 x 1 x y 42 2 P 1 x x x x x 42 2 r r 1 A 2 x A y r xA 1 r xx 0 2 y 42
- 172. S x y l’l S’ S’’ xx S y l l’ x S’ x S’’ Scope Frame Well-Bound Frame
- 173. Scope Frame Well-Typed Frame S x y l’l : T : T S’ S’’ xx v1 S y v2 l l’ x S’ x S’’
- 174. Good Frame Invariant S x y l’l S’ S’’ xx S y l l’ x S’ x S’’ Scope Frame Well-Bound Frame Scope Frame Well-Typed Frame S x y l’l : T : T S’ S’’ xx v1 S y v2 l l’ x S’ x S’’
- 175. : T x x x x x x …… Good Heap Invariant Every Frame is Well-Bound and Well-Typed Good Frame Good Frame
- 176. Architecture of a Specification Language-Independent Scopes Well- Boundness Well- Typedness Language-Specific Static Language-Independent Scopes Frames Well- Boundness Well- Typedness Dynamic Semantics A P I Language-Specific StaticDynamic Language-Independent Scopes Frames Language- Independent Lemmas Well- Boundness Well- Typedness Dynamic Semantics Type Soundness A P I Language-Specific StaticDynamicProofs
- 177. Type Soundness Principle Evaluation Preserves Good Heap Invariant Good Heap Good Heap Eval
- 178. Good heapGood heap Unreferenced Garbage Collection x x A Bx x A Bx x A Bx x A
- 179. The Paper and Artifact L1 (PCF) L2 (PCF+records) L3 (PCF+classes+i nheritance) github.com/metaborg/scopes-describe-frames Tech Report Consist ent * Complete * WellDocume nted*Easyto R euse* *Ev aluated * ECOOP* Artifact * AEC
- 180. What’s Next
- 181. Language Designer’s Workbench Language Semantics Tools IDEs Type Checkers Language Run Time Garbage Collector Static Semantics Dynamic Semantics Scope Graphs Frame Heaps Garbage Collector Proof Assistant Infrastructure
- 182. def fac(n : Int) : Int = { if (n == 0) 1 else n * fac(n - 1) }; fac(2); x 1 2 fac n xn fac fac x fac Fn 1 x n 2 2 n fac fac x n 1 2 x n 0 2 n P nfacnnnn PP Good Heap Scopes Describe Frames Type soundness Garbage collection soundness
- 183. Part V: Closure
- 185. Spoofax Language Workbench SDF3: Syntax Definition NaBL2: Static Semantics DynSem: Dynamic Semantics Programming Environment+ + http://spoofax.org
- 186. Syntax Definition in SDF3 Statement.If = < if(<Exp>) <Statement> else <Statement> > Parser Abstract syntax tree schema Pretty-printer Syntactic completion Folding rules Error recovery Syntactic coloring Outline rules {
- 187. Static Semantics in NaBL2 [[ FieldVar(e, f) ^ (s) : ty ]] := [[ e ^ (s) : ty_e ]], new s_use, Field{f} -> s_use, s_use -I-> s_rec, ty_e == RECORD(s_rec), Field{f} |-> d, d : ty. Name resolution Incremental analysis Name & type checking Code completion Refactoring (renaming) Type inference Program querying … {
- 188. Dynamic Semantics in DynSem App(ClosV(xs, e_body, E_clos), es) --> v' where bindArgs(xs, es) --> E_params; Env {E_params, E_clos} |- e_body --> v'. Interpreter Semantics preservation Type soundness checking Abstract interpretation … {


![/* A program to solve the 8-queens problem */
let
var N := 8
type intArray = array of int
var row := intArray [ N ] of 0
var col := intArray [ N ] of 0
var diag1 := intArray [N+N-1] of 0
var diag2 := intArray [N+N-1] of 0
function printboard() =
(for i := 0 to N-1
do (for j := 0 to N-1
do print(if col[i]=j then " O" else " .");
print("n"));
print("n"))
function try(c:int) =
( if c=N
then printboard()
else for r := 0 to N-1
do if row[r]=0 & diag1[r+c]=0 & diag2[r+7-c]=0
then (row[r]:=1; diag1[r+c]:=1; diag2[r+7-c]:=1;
col[c]:=r;
try(c+1);
row[r]:=0; diag1[r+c]:=0; diag2[r+7-c]:=0)
)
in try(0)
end
let function fact(n : int) : int =
if n < 1 then 1 else (n * fact(n -
1))
in fact(10)
end
/* define valid recursive types */
let
/* define a list */
type intlist = {hd: int, tl: intlist}
/* define a tree */
type tree ={key: int, children: treelist}
type treelist = {hd: tree, tl: treelist}
var lis:intlist := intlist { hd=0, tl=
nil }
in
lis
end
A Language Design
Tiger by Andrew Appel, 1996](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-2-320.jpg)
![Tiger by Andrew Appel, 1996
A Language Design
/* A program to solve the 8-queens problem */
let
var N := 8
type intArray = array of int
var row := intArray [ N ] of 0
var col := intArray [ N ] of 0
var diag1 := intArray [N+N-1] of 0
var diag2 := intArray [N+N-1] of 0
function printboard() =
(for i := 0 to N-1
do (for j := 0 to N-1
do print(if col[i]=j then " O" else " .");
print("n"));
print("n"))
function try(c:int) =
( if c=N
then printboard()
else for r := 0 to N-1
do if row[r]=0 & diag1[r+c]=0 & diag2[r+7-c]=0
then (row[r]:=1; diag1[r+c]:=1; diag2[r+7-c]:=1;
col[c]:=r;
try(c+1);
row[r]:=0; diag1[r+c]:=0; diag2[r+7-c]:=0)
)
in try(0)
end
let function fact(n : int) : int =
if n < 1 then 1 else (n * fact(n -
1))
in fact(10)
end
/* define valid recursive types */
let
/* define a list */
type intlist = {hd: int, tl: intlist}
/* define a tree */
type tree ={key: int, children: treelist}
type treelist = {hd: tree, tl: treelist}
var lis:intlist := intlist { hd=0, tl=
nil }
in
lis
end
Type Checker
Compiler
Interpreter
Parser](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-3-320.jpg)
![Tiger by Andrew Appel, 1996
A Language Design
/* A program to solve the 8-queens problem */
let
var N := 8
type intArray = array of int
var row := intArray [ N ] of 0
var col := intArray [ N ] of 0
var diag1 := intArray [N+N-1] of 0
var diag2 := intArray [N+N-1] of 0
function printboard() =
(for i := 0 to N-1
do (for j := 0 to N-1
do print(if col[i]=j then " O" else " .");
print("n"));
print("n"))
function try(c:int) =
( if c=N
then printboard()
else for r := 0 to N-1
do if row[r]=0 & diag1[r+c]=0 & diag2[r+7-c]=0
then (row[r]:=1; diag1[r+c]:=1; diag2[r+7-c]:=1;
col[c]:=r;
try(c+1);
row[r]:=0; diag1[r+c]:=0; diag2[r+7-c]:=0)
)
in try(0)
end
let function fact(n : int) : int =
if n < 1 then 1 else (n * fact(n -
1))
in fact(10)
end
/* define valid recursive types */
let
/* define a list */
type intlist = {hd: int, tl: intlist}
/* define a tree */
type tree ={key: int, children: treelist}
type treelist = {hd: tree, tl: treelist}
var lis:intlist := intlist { hd=0, tl=
nil }
in
lis
end
Type Checker
Compiler
Interpreter
Parser](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-4-320.jpg)
![Tiger by Andrew Appel, 1996
A Language Design
/* A program to solve the 8-queens problem */
let
var N := 8
type intArray = array of int
var row := intArray [ N ] of 0
var col := intArray [ N ] of 0
var diag1 := intArray [N+N-1] of 0
var diag2 := intArray [N+N-1] of 0
function printboard() =
(for i := 0 to N-1
do (for j := 0 to N-1
do print(if col[i]=j then " O" else " .");
print("n"));
print("n"))
function try(c:int) =
( if c=N
then printboard()
else for r := 0 to N-1
do if row[r]=0 & diag1[r+c]=0 & diag2[r+7-c]=0
then (row[r]:=1; diag1[r+c]:=1; diag2[r+7-c]:=1;
col[c]:=r;
try(c+1);
row[r]:=0; diag1[r+c]:=0; diag2[r+7-c]:=0)
)
in try(0)
end
let function fact(n : int) : int =
if n < 1 then 1 else (n * fact(n -
1))
in fact(10)
end
/* define valid recursive types */
let
/* define a list */
type intlist = {hd: int, tl: intlist}
/* define a tree */
type tree ={key: int, children: treelist}
type treelist = {hd: tree, tl: treelist}
var lis:intlist := intlist { hd=0, tl=
nil }
in
lis
end
Type Checker
Compiler
Interpreter
Parser
Spoofax
{](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-5-320.jpg)





























![Declarative Disambiguation
parse filter
Disambiguation Filters [Klint & Visser; 1994], [Van den Brand, Scheerder, Vinju, Visser; CC 2002]](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-36-320.jpg)
![Priority and Associativity
context-free syntax
Expr.Int = INT
Expr.Add = <<Expr> + <Expr>> {left}
Expr.Mul = <<Expr> * <Expr>> {left}
context-free priorities
Expr.Mul > Expr.Add
Recent improvement: safe disambiguation of operator precedence [Afroozeh et al. SLE13, Onward15]
Add
VarRef VarRef
“y”“x”
Mul
Int
“3”
Add
VarRef
VarRef
“y”
“x”
Mul
Int
“3”
3 * x + y](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-37-320.jpg)



![Tiger Syntax: Lexical Syntax
module Identifiers
lexical syntax
Id = [a-zA-Z] [a-zA-Z0-9_]*
lexical restrictions
Id -/- [a-zA-Z0-9_]
lexical syntax
Id = "nil" {reject}
Id = "let" {reject}
Id = … {reject}
module Strings
sorts StrConst
lexical syntax
StrConst = """ StrChar* """
StrChar = ~["n]
StrChar = [] [n]
StrChar = [] [t]
StrChar = [] [^] [A-Z]
StrChar = [] [0-9] [0-9] [0-9]
StrChar = [] ["]
StrChar = [] []
StrChar = [] [ tn]+ []
context-free syntax // records
Exp.String = StrConst](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-41-320.jpg)
![Tiger Syntax: Whitespace
module Whitespace
lexical syntax
LAYOUT = [ tnr]
CommentChar = [*]
LAYOUT = "/*" InsideComment* "*/"
InsideComment = ~[*]
InsideComment = CommentChar
LAYOUT = SingleLineComment
SingleLineComment = "//" ~[nr]* NewLineEOF
NewLineEOF = [nr]
NewLineEOF = EOF
EOF =
lexical restrictions
// Ensure greedy matching for lexicals
CommentChar -/- [/]
EOF -/- ~[]
context-free restrictions
// Ensure greedy matching for comments
LAYOUT? -/- [ tnr]
LAYOUT? -/- [/].[/]
LAYOUT? -/- [/].[*]](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-42-320.jpg)

![Tiger Syntax: Numbers
module Numbers
lexical syntax
IntConst = [0-9]+
lexical syntax
RealConst.RealConstNoExp = IntConst "." IntConst
RealConst.RealConst = IntConst "." IntConst "e" Sign IntConst
Sign = "+"
Sign = "-"
context-free syntax
Exp.Int = IntConst
Exp.Uminus = [- [Exp]]
Exp.Times = [[Exp] * [Exp]] {left}
Exp.Divide = [[Exp] / [Exp]] {left}
Exp.Plus = [[Exp] + [Exp]] {left}
Exp.Minus = [[Exp] - [Exp]] {left}
Exp.Eq = [[Exp] = [Exp]] {non-assoc}
Exp.Neq = [[Exp] <> [Exp]] {non-assoc}
Exp.Gt = [[Exp] > [Exp]] {non-assoc}
Exp.Lt = [[Exp] < [Exp]] {non-assoc}
Exp.Geq = [[Exp] >= [Exp]] {non-assoc}
Exp.Leq = [[Exp] <= [Exp]] {non-assoc}
Exp.And = [[Exp] & [Exp]] {left}
Exp.Or = [[Exp] | [Exp]] {left}
context-free priorities
{Exp.Uminus}
> {left :
Exp.Times
Exp.Divide}
> {left :
Exp.Plus
Exp.Minus}
> {non-assoc :
Exp.Eq
Exp.Neq
Exp.Gt
Exp.Lt
Exp.Geq
Exp.Leq}
> Exp.And
> Exp.Or](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-44-320.jpg)
![Tiger Syntax: Records, Arrays, Types
module Records
imports Base
imports Identifiers
imports Types
context-free syntax // records
Type.RecordTy = <
{
<{Field ", n"}*>
}
>
Field.Field = <<Id> : <TypeId>>
Exp.NilExp = <nil>
Exp.Record = <<TypeId>{ <{InitField ", "}*> }>
InitField.InitField = <<Id> = <Exp>>
LValue.FieldVar = <<LValue>.<Id>>
module Arrays
imports Types
context-free syntax // arrays
Type.ArrayTy = <array of <TypeId>>
Exp.Array = <<TypeId>[<Exp>] of <Exp>>
LValue.Subscript = <<LValue>[<Index>]>
Index = Exp
module Types
imports Identifiers
imports Bindings
sorts Type
context-free syntax // type declarations
Dec.TypeDecs = <<{TypeDec "n"}+>> {longest-match}
TypeDec.TypeDec = <type <Id> = <Type>>
context-free syntax // type expressions
Type = TypeId
TypeId.Tid = Id
sorts Ty
context-free syntax // semantic types
Ty.INT = <INT>
Ty.STRING = <STRING>
Ty.NIL = <NIL>
Ty.UNIT = <UNIT>
Ty.NAME = <NAME <Id>>
Ty.RECORD = <RECORD <Id>>
Ty.ARRAY = <ARRAY <Ty> <Id>>
Ty.FUN = <FUN ( <{Ty ","}*> ) <Ty>>](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-45-320.jpg)













































![Representation
- ?
Declarative Rules
- ?
Language-Independent Tooling
- Name resolution
- Code completion
- Refactoring
- …
Separation of Concerns in Name Binding
Scope (& Type) Constraint Rules [PEPM16]
Scope Graphs](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-92-320.jpg)

![Scope Graph Constraints
new s // new scope
s1 -L-> s2 // labeled edge from scope s1 to scope s2
N{x} <- s // x is a declaration in scope s for namespace N
N{x} -> s // x is a reference in scope s for namespace N
N{x} |-> d // x resolves to declaration d
[[ e ^ (s) ]] // constraints for expression e in scope s](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-94-320.jpg)
![let
var x : int := x + 1
in
x + 1
end
s
s_bodyx
x
Let(
[VarDec(
"x"
, Tid("int")
, Plus(Var("x"), Int("1"))
)]
, [Plus(Var("x"), Int("1"))]
)
[[ Let([VarDec(x, t, e)], [e_body]) ^ (s) ]] :=
new s_body, // new scope
s_body -P-> s, // parent edge to enclosing scope
Var{x} <- s_body, // x is a declaration in s_body
[[ e ^ (s) ]], // init expression
[[ e_body ^ (s_body) ]]. // body expression
[[ Var(x) ^ (s') ]] :=
Var{x} -> s', // x is a reference in s'
Var{x} |-> d, // check that x resolves to a declaration
s’
x
?
P](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-95-320.jpg)

![Type Constraints
d : ty // declaration has type
t1 == ty2 // type equality
ty1 <! ty2 // declare sub-type
ty1 <? ty2 // query sub-type
. . . // extensions
[[ e ^ (s) : ty ]] // type of expression in scope](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-97-320.jpg)
![s
s_bodyx
x
[[ Let([VarDec(x, t, e)], [e_body]) ^ (s) : ty' ]] :=
new s_body, // new scope
s_body -P-> s, // parent edge to enclosing scope
Var{x} <- s_body, // x is a declaration in s_body
Var{x} : ty, // associate type
[[ t ^ (s) : ty ]], // type of type
[[ e ^ (s) : ty ]], // type of expression
[[ e_body ^ (s_body) : ty' ]]. // constraints for body
[[ Var(x) ^ (s') : ty ]] :=
Var{x} -> s', // x is a reference in s'
Var{x} |-> d, // check that x resolves to a declaration
d : ty. // type of declaration is type of reference
s’
x
let
var x : int := x + 1
in
x + 1
end
Let(
[VarDec(
"x"
, Tid("int")
, Plus(Var("x"), Int("1"))
)]
, [Plus(Var("x"), Int("1"))]
)
INT](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-98-320.jpg)
![let
type point = {x : int, y : int}
var origin : point := …
in origin.x
end
S2
S3
x
x
point
[[ FieldVar(e, f) ^ (s) : ty ]] :=
[[ e ^ (s) : ty_e ]],
new s_use,
Field{f} -> s_use,
s_use -I-> s_rec,
ty_e == RECORD(s_rec),
Field{f} |-> d,
d : ty.
[[ RecordTy(fields) ^ (s) : ty ]] :=
ty == RECORD(s_rec),
new s_rec,
Map2[[ fields ^ (s_rec, s) ]].
[[ Field(x, t) ^ (s_rec, s_outer) ]] :=
Field{x} <- s_rec,
Field{x} : ty !,
[[ t ^ (s_outer) : ty ]].
S1 point
s_rec
y
RECORD
INT
origin
origin
s_use
s_recty_e
Type Dependent Name Resolution](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-99-320.jpg)
![Tiger Names & Types: Composition
module statics/tiger
imports statics/arrays
imports statics/base
imports statics/bindings
imports statics/control-flow
imports statics/functions
imports statics/nabl-lib
imports statics/numbers
imports statics/records
imports statics/strings
imports statics/types
imports statics/variables
rules // top-level module
[[ Mod(e) ^ (s) : ty ]] :=
[[ e ^ (s) : ty ]].](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-100-320.jpg)
![Tiger Names & Types: Composition
module statics/functions
imports signatures/Functions-sig
imports statics/nabl-lib
imports statics/base
rules // function declarations
Dec[[ FunDecs(fdecs) ^ (s, s_outer) ]] :=
Map2[[ fdecs ^ (s, s_outer) ]].
[[ FunDec(f, args, t, e) ^ (s, s_outer) ]] :=
new s_fun,
s_fun -P-> s,
distinct/name D(s_fun) | error $[duplicate argument] @ NAMES,
MapTs2[[ args ^ (s_fun, s_outer) : tys ]],
[[ t ^ (s_outer) : ty ]],
Var{f} <- s,
Var{f} : FUN(tys, ty) !,
[[ e ^ (s_fun) : ty_body ]],
ty == ty_body| error $[return type does not match body] @ t.
[[ FArg(x, t) ^ (s_fun, s_outer) : ty ]] :=
Var{x} <- s_fun,
Var{x} : ty !,
[[ t ^ (s_outer) : ty ]].
rules // function calls
[[ Call(f, exps) ^ (s) : ty ]] :=
Var{f} -> s,
Var{f} |-> d | error $[Function [f] not declared],
d : FUN(tys, ty) | error $[Function expected] ,
MapSTs[[ exps ^ (s) : tys ]].](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-101-320.jpg)
![Tiger Names & Types: Composition
module statics/bindings
imports signatures/Bindings-sig
imports statics/nabl-lib
imports statics/base
imports statics/control-flow
imports statics/variables
rules // let
[[ Let(blocks, exps) ^ (s) : ty ]] :=
new s_body,
Decs[[ blocks ^ (s, s_body) ]],
Seq[[ exps ^ (s_body) : ty ]],
distinct D(s_body).
Decs[[ [] ^ (s_outer, s_body) ]] :=
s_body -P-> s_outer.
Decs[[ [block] ^ (s_outer, s_body) ]] :=
s_body -P-> s_outer,
Dec[[ block ^ (s_body, s_outer) ]].
Decs[[ [block | blocks@[_|_]] ^ (s_outer, s_body) ]] :=
new s_dec,
s_dec -P-> s_outer,
Dec[[ block ^ (s_dec, s_outer) ]],
Decs[[ blocks ^ (s_dec, s_body) ]],
distinct/name D(s_dec) | error $[duplicate declaration] @NAMES.
// Nested scopes: The scope of a variable or parameter includes the
// bodies of any function definitions in that scope. That is, access
// to variables in outer scopes is permitted, as in Pascal and Algol
/* Local redeclarations: A variable or function declaration may be
hidden by the redeclaration of the same name (as a variable or
function) in a smaller scope; for example, this function prints
"6 7 6 8 6" when applied to 5:
let
function f(v : int) =
let var v := 6
in print(v);
let var v := 7 in print(v) end;
print(v);
let var v := 8 in print(v) end;
print(v)
end
in f(4)
end
*/](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-102-320.jpg)
![Tiger Names & Types: Variables
module statics/variables
imports signatures/Variables-sig
imports statics/nabl-lib
imports statics/base
rules // variable declarations
Dec[[ VarDec(x, t, e) ^ (s, s_outer) ]] :=
[[ t ^ (s_outer) : ty1 ]],
[[ e ^ (s_outer) : ty2 ]],
ty2 <? ty1 | error $[type mismatch got [ty2] where [ty1] expected] @ e,
Var{x} <- s,
Var{x} : ty1 !.
Dec[[ VarDecNoType(x, e) ^ (s, s_outer) ]] :=
[[ e ^ (s_outer) : ty ]],
ty != NIL() | error $[explicit type expected for variable initialized with nil],
Var{x} <- s,
Var{x} : ty !.
rules // variable references
[[ Var(x) ^ (s) : ty ]] :=
Var{x} -> s, // declare x as variable reference
Var{x} |-> d, // check that x resolves to a declaration
d : ty. // type of declaration is type of reference
rules // statements
[[ Assign(e1, e2) ^ (s) : UNIT() ]] :=
[[ e1 ^ (s) : ty1 ]],
[[ e2 ^ (s) : ty2 ]],
ty2 <? ty1 | error $[type mismatch got [ty2] where [ty1] expected] @ e2.](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-103-320.jpg)
![Tiger Names & Types: Records (1)
module statics/records
imports signatures/Records-sig
imports statics/nabl-lib
imports statics/base
rules // record type
[[ RecordTy(fields) ^ (s) : ty ]] :=
new s_rec,
ty == RECORD(s_rec),
NIL() <! ty,
distinct/name D(s_rec)/Field | error $[Duplicate declaration of field [NAME]] @ NAMES,
Map2[[ fields ^ (s_rec, s) ]].
[[ Field(x, t) ^ (s_rec, s_outer) ]] :=
Field{x} <- s_rec,
Field{x} : ty !,
[[ t ^ (s_outer) : ty ]].](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-104-320.jpg)
![Tiger Names & Types: Records (2)
module statics/records
…
rules // record creation
[[ r@Record(t, inits) ^ (s) : ty ]] :=
[[ t ^ (s) : ty ]],
ty == RECORD(s_rec) | error $[record type expected],
new s_use, s_use -I-> s_rec,
D(s_rec)/Field subseteq/name R(s_use)/Field | error $[Field [NAME] not initialized] @r,
distinct/name R(s_use)/Field | error $[Duplicate initialization of field [NAME]] @NAMES,
Map2[[ inits ^ (s_use, s) ]].
[[ InitField(x, e) ^ (s_use, s) ]] :=
Field{x} -> s_use,
Field{x} |-> d,
d : ty1,
[[ e ^ (s) : ty2 ]],
ty2 <? ty1 | error $[type mismatch got [ty2] where [ty1] expected].
rules // record field access
[[ FieldVar(e, f) ^ (s) : ty ]] :=
[[ e ^ (s) : ty_e ]],
ty_e == RECORD(s_rec),
new s_use,
s_use -I-> s_rec,
Field{f} -> s_use,
Field{f} |-> d,
d : ty.](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-105-320.jpg)
![Tiger Names & Types: Records (2)
module statics/arrays
imports signatures/Arrays-sig
imports statics/nabl-lib
imports statics/base
rules // array type
[[ ArrayTy(t) ^ (s) : ARRAY(ty, s')]] :=
new s', // unique token to distinghuish the array type
[[ t ^ (s) : ty ]].
rules // array creation
[[ Array(t, e1, e2) ^ (s) : ty ]] :=
[[ t ^ (s) : ty ]],
ty == ARRAY(ty_elem, s_arr) | error $[array type expected],
ty_elem2 <? ty_elem | error $[type mismatch [ty_indic] expected] @ e2,
[[ e1 ^ (s) : INT() ]], // length
[[ e2 ^ (s) : ty_elem2 ]]. // initial value
rules // array indexing
[[ Subscript(e1, e2) ^ (s) : ty ]] :=
[[ e1 ^ (s) : ty_arr ]],
ty_arr == ARRAY(ty, s_arr),
[[ e2 ^ (s) : INT() ]].](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-106-320.jpg)
![Tiger Names & Types: Numbers
module statics/numbers
imports signatures/Numbers-sig
imports statics/nabl-lib
imports statics/base
rules // literals
[[ Int(i) ^ (s) : INT() ]].
rules // operators
[[ Uminus(e) ^ (s) : INT() ]] :=
[[ e ^ (s) : INT() ]].
[[ Divide(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : INT() ]], [[ e2 ^ (s): INT() ]].
[[ Times(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : INT() ]], [[ e2 ^ (s): INT() ]].
[[ Minus(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : INT() ]], [[ e2 ^ (s): INT() ]].
[[ Plus(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : INT() ]], [[ e2 ^ (s): INT() ]].
[[ Eq(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]],
ty1 == ty2.
[[ Neq(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]],
ty1 == ty2.
[[ Gt(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]],
ty1 == ty2.
[[ Lt(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]],
ty1 == ty2.
[[ Geq(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]],
ty1 == ty2.
[[ Leq(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]],
ty1 == ty2.
[[ Or(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]],
ty1 == ty2.
[[ And(e1, e2) ^ (s) : INT() ]] :=
[[ e1 ^ (s) : ty1 ]], [[ e2 ^ (s): ty2 ]],
ty1 == ty2.](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-107-320.jpg)
![Tiger Names & Types: Numbers
module statics/control-flow
imports signatures/Control-Flow-sig
imports statics/nabl-lib
imports statics/base
rules // sequence
Seq[[ [] ^ (s) : UNIT() ]].
Seq[[ [e] ^ (s) : ty ]] :=
[[ e ^ (s) : ty ]].
Seq[[ [ e | es@[_|_] ] ^ (s) : ty ]] :=
[[ e ^ (s) : ty' ]], Seq[[ es ^ (s) : ty ]].
[[ Seq(es) ^ (s) : ty ]] :=
Seq[[ es ^ (s) : ty ]].
[[ If(e1, e2, e3) ^ (s) : ty2 ]] :=
[[ e1 ^ (s) : INT() ]],
[[ e2 ^ (s) : ty2 ]],
[[ e3 ^ (s) : ty3 ]],
ty2 == ty3 | error $[branches should have same type].
[[ IfThen(e1, e2) ^ (s) : UNIT() ]] :=
[[ e1 ^ (s) : INT() ]],
[[ e2 ^ (s) : UNIT() ]].
[[ While(e1, e2) ^ (s) : UNIT() ]] :=
new s', s' -P-> s,
Loop{""} <- s',
[[ e1 ^ (s) : INT() ]],
[[ e2 ^ (s') : UNIT() ]].
[[ stm@For(Var(x), e1, e2, e3) ^ (s) : UNIT() ]] :=
new s_for,
s_for -P-> s,
Var{x} <- s_for,
Var{x} : INT(),
Loop{Break()@stm} <- s_for,
[[ e1 ^ (s) : INT() ]], // x not bound in loop bounds
[[ e2 ^ (s) : INT() ]],
[[ e3 ^ (s_for) : UNIT() ]]. // x bound in body
[[ stm@Break() ^ (s) : UNIT() ]] :=
Loop{Break()@stm} -> s,
Loop{Break()@stm} |-> d.](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-108-320.jpg)


![Domain-Specific Languages
- Ice Dust2 [ECOOP17]
- Green-Marl (Oracle)
Education
- Mini-Java, Tiger, Calc
Programming languages
- Pascal, TypeScript, F#
- (student projects in progress)
Bootstrapping language workbench
- NaBL2, …
Applications](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-111-320.jpg)
![Scopes Describe Frames [ECOOP16]
S
x
y
l’l
: T
: T
S’ S’’
xx
S
y
l l’
x
S’
x
S’’
A Uniform Model for Memory Layout
in Dynamic Semantics](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-112-320.jpg)



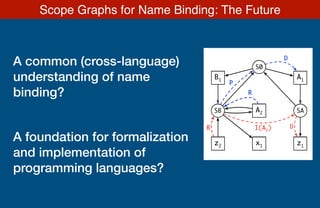








![Structural Operational (Small-Step) Semantics
e1 ➞ e1’
ifz(e1) e2 else e3 ➞ ifz(e1’) e2 else e3
i != 0
ifz(i) e2 else e3 ➞ e3
ifz(0) e2 else e3 ➞ e2
(x.e) v1 ➞ e[x := v1]
e1 ➞ e1’
e1 e2 ➞ e1’ e2
e2 ➞ e2’
v e2 ➞ v e2’
e1 ➞ e1’
e1 + e2 ➞ e1’ + e2
e2 ➞ e2’
e1 + e2 ➞ e1 + e2’
i + j ➞ i + j
e ➞ e
reducing expressions
e = x | i | e + e | x.e | e e | ifz(e) e else e
order of evaluation?](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-125-320.jpg)
![Natural (Big-Step) Semantics
E ⊢ e1 NumV(i)
E ⊢ e2 NumV(j)
E ⊢ e1 + e2 NumV(i + j)
E[x] = v
E ⊢ x v
E ⊢ x.e ClosV(x, e, E)
E ⊢ i NumV(i)
E ⊢ e1 NumV(0)
E ⊢ e2 v
E ⊢ if(e1) e2 else e3 v
E ⊢ e1 NumV(i), i != 0
E ⊢ e3 v
E ⊢ if(e1) e2 else e3 v
E1 ⊢ e1 ClosV(x, e, E2)
E1 ⊢ e2 v1
{x ↦ v1, E2} ⊢ e v2
E1 ⊢ e1 e2 v2
E ⊢ e v
reducing expressions to values
e = x | i | e + e | x.e | e e | ifz(e) e else e](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-126-320.jpg)


![Abstract Syntax from Concrete Syntax
module Arithmetic
imports Expressions
imports Common
context-free syntax
Expr.Num = INT
Expr.Plus = [[Expr] + [Expr]] {left}
Expr.Minus = [[Expr] - [Expr]] {left}
Expr.Times = [[Expr] * [Expr]] {left}
Expr.Mod = [[Expr] % [Expr]] {left}
context-free priorities
{left: Expr.Times Expr.Mod }
> {left: Expr.Minus Expr.Plus }
module Arithmetic-sig
imports Expressions-sig
imports Common-sig
signature
sorts
Expr
constructors
Num : INT -> Expr
Plus : Expr * Expr -> Expr
Minus : Expr * Expr -> Expr
Times : Expr * Expr -> Expr
Mod : Expr * Expr -> Expr
src-gen/ds-signatures/Arithmetic-sig](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-129-320.jpg)






![Immutable Variables: Environment Passing
module variables
imports Variables-sig environment
rules
E |- Let(x, v: V, e2) --> v2
where
Env {x |--> v, E} |- e2 --> v2.
E |- Var(x) --> E[x].
constructors
Fun : ID * Expr -> Expr
App : Expr * Expr -> Expr
module environment
imports values
signature
sort aliases
Env = Map<String, V>
variables
E : Env](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-136-320.jpg)
![First-Class Functions: Environment in Closure
module unary-functions
imports expressions environment
signature
constructors
ClosV : String * Expr * Env -> V
rules
E |- Fun(x, e) --> ClosV(x, e, E).
E |- App(e1, e2) --> v
where
E |- e1 --> ClosV(x, e, E');
E |- e2 --> v2;
Env {x |--> v2, E'} |- e --> v.
constructors
Fun : ID * Expr -> Expr
App : Expr * Expr -> Expr
module environment
imports values
signature
sort aliases
Env = Map<String, V>
variables
E : Env
module variables
imports Variables-sig environment
rules
E |- Let(x, v: V, e2) --> v2
where
Env {x |--> v, E} |- e2 --> v2.
E |- Var(x) --> E[x].](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-137-320.jpg)

![Mutable Boxes: Store
module box
imports store arithmetic
signature
constructors
Box : Expr -> Expr
Unbox : Expr -> Expr
SetBox : Expr * Expr -> Expr
constructors
BoxV: Int -> V
rules
Box(e) :: S --> BoxV(loc) :: Store {loc |--> v, S'}
where e :: S --> v :: S';
fresh => loc.
Unbox(BoxV(loc)) :: S --> S[loc].
SetBox(BoxV(loc), v) :: S --> v :: Store {loc |--> v, S}.
module store
imports values
signature
sort aliases
Store = Map<Int, V>
variables
S : Store](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-139-320.jpg)
![Mutable Variables: Environment + Store
constructors
Let : ID * Expr * Expr -> Expr
Var : ID -> Expr
Set : String * Expr -> Expr
module variables-mutable
imports Variables-sig store
rules
E |- Var(x) :: S --> v :: S
where E[x] => loc; S[loc] => v.
E |- Let(x, v, e2) :: S1 --> v2 :: S3
where
fresh => loc;
{loc |--> v, S1} => S2;
Env {x |--> loc, E} |- e2 :: S2 --> v2 :: S3.
E |- Set(x, v) :: S --> v :: Store {loc |--> v, S}
where E[x] => loc.
module store
imports values
signature
sort aliases
Env = Map<ID, Int>
Store = Map<Int, V>
variables
E : Env
S : Store](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-140-320.jpg)

![Abstraction: Env/Store Meta Functions
module store
imports values
signature
sort aliases
Env = Map<String, Int>
Store = Map<Int, V>
variables
E : Env
S : Store
constructors
readVar : String --> V
bindVar : String * V --> Env
writeVar : String * V --> V
allocate : V --> Int
write : Int * V --> V
read : Int --> V
rules
allocate(v) --> loc
where
fresh => loc;
write(loc, v) --> _.
write(loc, v) :: S -->
v :: Store {loc |--> v, S}.
read(loc) :: S --> S[loc] :: S.
rules
bindVar(x, v) --> {x |--> loc}
where allocate(v) --> loc.
E |- readVar(x) --> read(E[x]).
E |- writeVar(x, v) --> write(E[x], v).](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-142-320.jpg)


![Functions with Multiple Arguments
module functions
imports Functions-sig
imports variables
signature
constructors
ClosV : List(ID) * Expr * Env -> V
bindArgs : List(ID) * List(Expr) --> Env
rules
E |- Fun(xs, e) --> ClosV(xs, e, E).
App(ClosV(xs, e_body, E_clos), es) --> v'
where
bindArgs(xs, es) --> E_params;
Env {E_params, E_clos} |- e_body --> v'.
bindArgs([], []) --> {}.
bindArgs([x | xs], [e | es]) --> {E, E'}
where
bindVar(x, e) --> E;
bindArgs(xs, es) --> E'.](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-145-320.jpg)














![S
x
y
l’l
S’ S’’
xx
S
y
l l’
x
S’
x
S’’
Scope Frame
[ESOP’15] [ECOOP’16]](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-160-320.jpg)
![1 x1
2
x
yx
1
2
x
yx
R
1
2
x
yx
R
P
1
2
x
yx
R
P
D
P
scope
declaration
reference
scope edgel
val x = 31;
val y = x + 11;
Lexical Scoping
[ESOP’15; PEPM’16]](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-161-320.jpg)

![More Binding Patterns
Shadowing
S0
S1
S2
D < P.p
s.p < s.p’
p < p’
S1
S2
x1
y1
y2 x2
z1
x3S0z2
def x3 = z2 5 7
def z1 =
fun x1 {
fun y1 {
x2 + y2
}
}
S1
S2
x1
y1
y2 x2
z1
x3S0z2
R
P
P
D
S1
S2
x1
y1
y2 x2
z1
x3S0z2
D
P
R
R
P
P
D
R.P.D < R.P.P.D
Java Import
package p1;
imports r2.*;
imports q3.E4;
public class C5 {}
class D6 {}
4
p1
D6C5
3
2r2
1
p1
E4
q3
Java Packages
package p3;
class D4 {}
package p1;
class C2 {}
1 p3p1
2
p1 p3
3
D4C2
C# Namespaces and Partial Classes
namespace N1 {
using M2;
partial class C3 {
int f4;
}
}
namespace N5 {
partial class C6 {
int m7() {
return f8;
}
}
}
1
3 6
4 7
8
C3 C6
N1 N5
f4 m7
N1 N5
C3 C6
f8
2 M2 5
Transitive vs. Non-Transitive
With transitive imports, a well formed path is R.P*.I(_)*.D
With non-transitive imports, a well formed path is R.P*.I(_)?
.D
A1
SA
z1
B1
SB
S0
A2
C1
SCz2
x1 B2
A1
SA
z1
B1
SB
S0
A2
I(A2
)
D
C1
SCz2
I(B2
)
R
x1 B2
??
module A1 {
def z1 = 5
}
module B1 {
import A2
}
module C1 {
import B2
def x1 = 1 + z2
}
SA
SB
SC
[ESOP’15]
Qualified Names
module N1 {
def s1 = 5
}
module M1 {
def x1 = 1 + N2.s2
}
S0
N1
SN
s2
S0
N2
R
D
R
I(N2) D
X1
s1
N1
SN
s2
S0
N2
R
D
X1
s1
N1
SN
s2
S0
N2
X1
s1](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-163-320.jpg)


![S
x
y
l’l
S’ S’’
xx
S
y
l l’
x
S’
x
S’’
Scope Frame
[ECOOP’16]
Slots
Links](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-166-320.jpg)










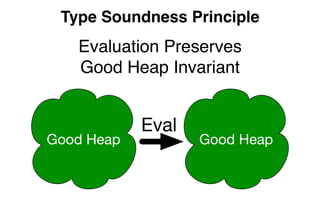








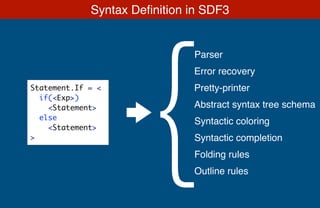
![Static Semantics in NaBL2
[[ FieldVar(e, f) ^ (s) : ty ]] :=
[[ e ^ (s) : ty_e ]],
new s_use,
Field{f} -> s_use,
s_use -I-> s_rec,
ty_e == RECORD(s_rec),
Field{f} |-> d,
d : ty.
Name resolution
Incremental analysis
Name & type checking
Code completion
Refactoring (renaming)
Type inference
Program querying
…
{](https://image.slidesharecdn.com/spoofax-ecoop-summerschool-2017-170714204825/85/Declarative-Language-Definition-187-320.jpg)
