![6
First Order Difference
First order difference is the difference of function value at poitn xn from
function value xn+1. It is represented by
∆f[xn] = f[xn+1] − f[xn]
x
y b
b
b
1.86
-0.65
-1.56
b
1
b
2.7
b
4.5
First order difference of the function values in function plot within the
domain 1 ≤ x ≤ 2.7 are −0.65 − 1.86 = −2.51 and −1.56 − (−0.65) = −0.91
respectively. These differences have “negative sign” (do not compare the
magnitude). So, function is decreasing function.
x
y
b
b
b
-1.56
-0.84
1.49
b
1
b
2.7
b
4.5
First order difference of the function values in function plot in the domain
2.7 ≤ x ≤ 4.5 are −0.84 − (−1.56) = 0.72 and 1.49 − (−0.84) = 2.33
respectively. These differences have “positive sign” (do not compare the
magnitude). So, function is increasing function.](https://image.slidesharecdn.com/decreasingincreasingfunctionsbyarunumrao-211013171202-211017115936/85/Decreasing-increasing-functions-by-arun-umrao-6-320.jpg)
![7
Difference Table
Consider a function f(x) = x2
− 5.5x + 6. We have to check, where function
is increasing and decreasing. Take two arbitrary limits, say x = 0 to x =
3. Take 30 points within this limits. The points xn are 0, 0.1, . . ., 3.0.
The function values at these points are computed using Excel software and
relation
∆f[xn] = f[xn+1] − f[xn]
x f(x) ∆f(x) x f(x) ∆f(x)
0.00 6.00 -0.54 1.60 -0.24 -0.22
0.10 5.46 -0.52 1.70 -0.46 -0.20
0.20 4.94 -0.50 1.80 -0.66 -0.18
0.30 4.44 -0.48 1.90 -0.84 -0.16
0.40 3.96 -0.46 2.00 -1.00 -0.14
0.50 3.50 -0.44 2.10 -1.14 -0.12
0.60 3.06 -0.42 2.20 -1.26 -0.10
0.70 2.64 -0.40 2.30 -1.36 -0.08
0.80 2.24 -0.38 2.40 -1.44 -0.06
0.90 1.86 -0.36 2.50 -1.50 -0.04
1.00 1.50 -0.34 2.60 -1.54 -0.02
1.10 1.16 -0.32 2.70 -1.56 0.00
1.20 0.84 -0.30 2.80 -1.56 0.02
1.30 0.54 -0.28 2.90 -1.54 0.04
1.40 0.26 -0.26 3.00 -1.50 0.06
1.50 0.00 -0.24 3.10 -1.44
To check the curve of function f(x) that, where it is increasing and where
it is decreasing, we observe the “sign” of ∆f(x), i.e. “sing” of first order
difference. The domain of x for which “sign” of ∆f(x) is “negative”, function
is continuously decreasing there. Similarly, the domain of x for which “sign”
of ∆f(x) is “positive”, function is continuous increasing there.](https://image.slidesharecdn.com/decreasingincreasingfunctionsbyarunumrao-211013171202-211017115936/85/Decreasing-increasing-functions-by-arun-umrao-7-320.jpg)
Decreasing increasing functions by arun umrao
- 1. 1 FUNCTION ANALYSIS JANUARY 1, 2006 Arun Umrao www.sites.google.com/view/arunumrao DRAFT COPY - GPL LICENSING
- 2. 2 What is function? 1. A function f relates with each element of x of a set, say Df , with exactly one element y of another set, say Rf . 2. Df is called domain of function f. 3. Rf is called range of function f. 4. x is independent variable. 5. y is called dependent variable.
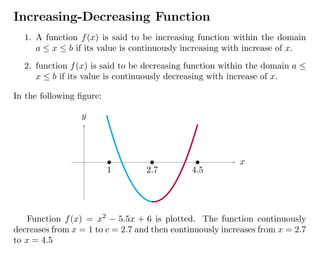
- 3. 3 Increasing-Decreasing Function 1. A function f(x) is said to be increasing function within the domain a ≤ x ≤ b if its value is continuously increasing with increase of x. 2. function f(x) is said to be decreasing function within the domain a ≤ x ≤ b if its value is continuously decreasing with increase of x. In the following figure: x y b 1 b 2.7 b 4.5 Function f(x) = x2 − 5.5x + 6 is plotted. The function continuously decreases from x = 1 to c = 2.7 and then continuously increases from x = 2.7 to x = 4.5
- 4. 4 Decreasing Function Decreasing function means, function value at xn is greater than function value at xn+1. For example, take three points in the domain 1 ≤ x ≤ 2.7 as x = 1, x = 1.85 and x = 2.7. x y b b b 1.86 -0.65 -1.56 b 1 b 2.7 b 4.5 Function values at these three points are 1.86, −0.65 and −1.56 respec- tively. It shows that each function value is less than its previous value and greater than next value.
- 5. 5 Increasing Function Increasing function means, function value at xn is less than function value at xn+1. For example, take three points in the domain 2.7 ≤ x ≤ 4.5 as x = 2.7, x = 3.6 and x = 4.5. x y b b b -1.56 -0.84 1.49 b 1 b 2.7 b 4.5 Function values at these three points are −1.56, −0.84 and 1.49 respec- tively. It shows that each function value is greater than its previous value and less than next value.
- 6. 6 First Order Difference First order difference is the difference of function value at poitn xn from function value xn+1. It is represented by ∆f[xn] = f[xn+1] − f[xn] x y b b b 1.86 -0.65 -1.56 b 1 b 2.7 b 4.5 First order difference of the function values in function plot within the domain 1 ≤ x ≤ 2.7 are −0.65 − 1.86 = −2.51 and −1.56 − (−0.65) = −0.91 respectively. These differences have “negative sign” (do not compare the magnitude). So, function is decreasing function. x y b b b -1.56 -0.84 1.49 b 1 b 2.7 b 4.5 First order difference of the function values in function plot in the domain 2.7 ≤ x ≤ 4.5 are −0.84 − (−1.56) = 0.72 and 1.49 − (−0.84) = 2.33 respectively. These differences have “positive sign” (do not compare the magnitude). So, function is increasing function.
- 7. 7 Difference Table Consider a function f(x) = x2 − 5.5x + 6. We have to check, where function is increasing and decreasing. Take two arbitrary limits, say x = 0 to x = 3. Take 30 points within this limits. The points xn are 0, 0.1, . . ., 3.0. The function values at these points are computed using Excel software and relation ∆f[xn] = f[xn+1] − f[xn] x f(x) ∆f(x) x f(x) ∆f(x) 0.00 6.00 -0.54 1.60 -0.24 -0.22 0.10 5.46 -0.52 1.70 -0.46 -0.20 0.20 4.94 -0.50 1.80 -0.66 -0.18 0.30 4.44 -0.48 1.90 -0.84 -0.16 0.40 3.96 -0.46 2.00 -1.00 -0.14 0.50 3.50 -0.44 2.10 -1.14 -0.12 0.60 3.06 -0.42 2.20 -1.26 -0.10 0.70 2.64 -0.40 2.30 -1.36 -0.08 0.80 2.24 -0.38 2.40 -1.44 -0.06 0.90 1.86 -0.36 2.50 -1.50 -0.04 1.00 1.50 -0.34 2.60 -1.54 -0.02 1.10 1.16 -0.32 2.70 -1.56 0.00 1.20 0.84 -0.30 2.80 -1.56 0.02 1.30 0.54 -0.28 2.90 -1.54 0.04 1.40 0.26 -0.26 3.00 -1.50 0.06 1.50 0.00 -0.24 3.10 -1.44 To check the curve of function f(x) that, where it is increasing and where it is decreasing, we observe the “sign” of ∆f(x), i.e. “sing” of first order difference. The domain of x for which “sign” of ∆f(x) is “negative”, function is continuously decreasing there. Similarly, the domain of x for which “sign” of ∆f(x) is “positive”, function is continuous increasing there.